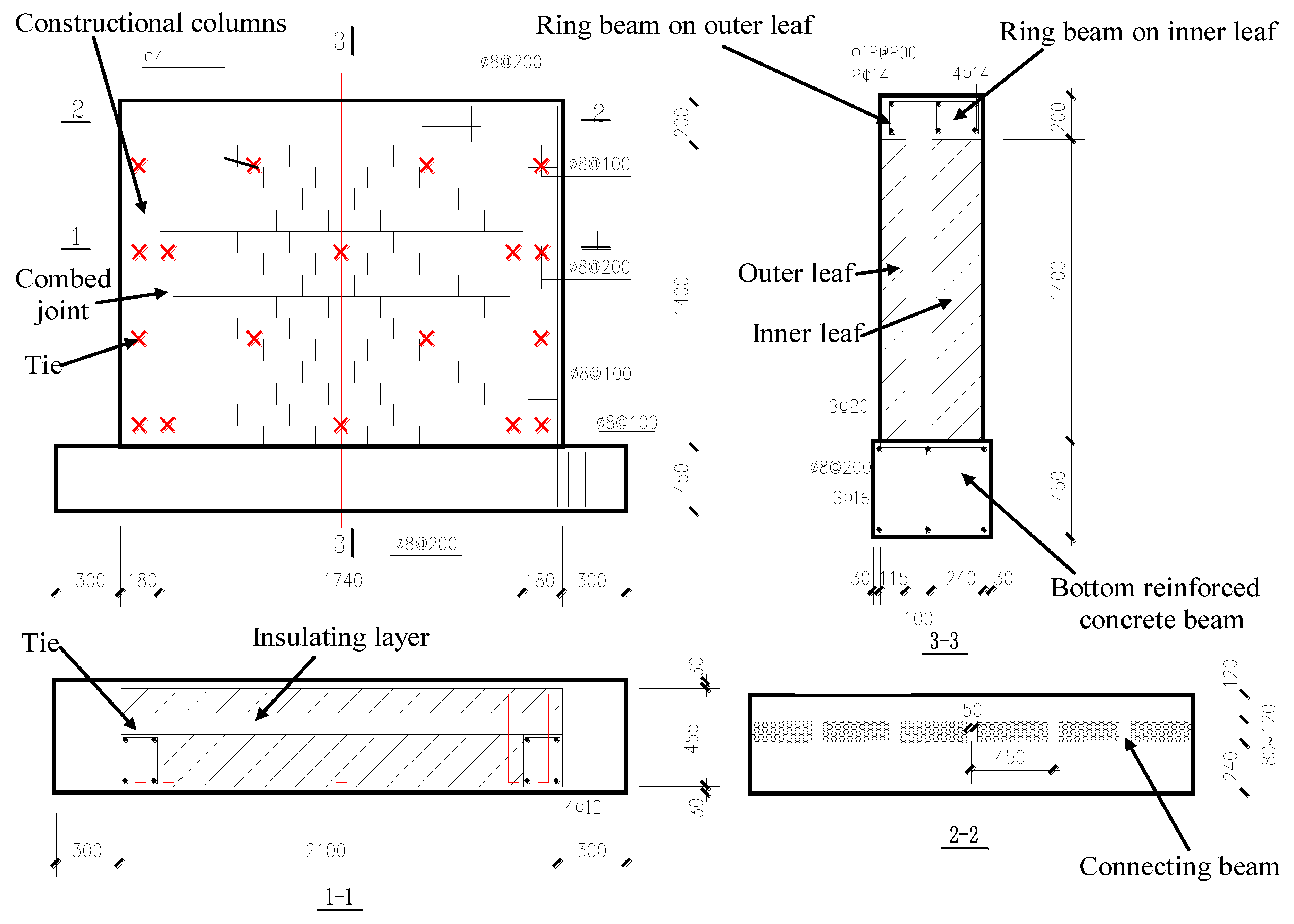
1. Introduction
Clay brick masonry cavity-walls were first implemented in construction back in the 19th century. Nicholson [
1] defined it as a hollow wall built in two thicknesses, having an inner cavity, either to save the number of materials used or to preserve the more uniform temperature in buildings. Load-bearing clay brick cavity-wall construction became commonly used in Europe, North America, Australia, and New Zealand since the second half of the 19th century [
2]. Cavity walls can either be infilled in structural frames or act as stand-alone bearing walls in commercial building construction owing to its thermal performance and resistance to fire, moisture penetration, and sound insulation. Such walls consist of two ‘skins’, commonly made of brick or concrete block masonry separated by a hollow cavity. A cavity wall combines three lines of defense: run-off along the exterior surface, absorption by the veneer wall, and run-off at the cavity side, with the cavity acting as a capillary break [
3]. There is a distinction between walls that are bridged by brickwork at frequent intervals, and what may be regarded as true cavity wall, with only iron ties, patent or other bricks, bridging it at spare intervals [
4,
5,
6].
The cavity is either left empty or filled with insulation using various methods. However, to increase energy efficiency, cavity filling gradually became normal practice [
7]. For cavity wall technology, higher thermal performance is achieved via placing insulation into increased cavity width. Generally, 40 mm of insulation is perceived as sufficient, resulting in an 80- or 100-mm cavity [
8]. The insulation can closely agglutinate the inner and outer leaf in the cavity without gap, cracks or insulation weak points, ensuring superior performance. Available techniques for insulating existing cavity walls generally involve injecting or blowing insulating material into the cavity. Three generic types of cavity wall insulation are commonly used, including mineral wool, beads/granules, and foamed insulation [
9,
10]. Polystyrene board is the most common thermal insulation in masonry cavity wall construction, with three other methods including the inner leaf, outer leaf, and tie. Several problems have hindered wider use of masonry cavity wall construction including: (1) the gap between polystyrene boards is too large, (2) polystyrene boards, inner and outer leaf cannot be closely integrated with each other, (3) and beam, window and balcony are weak links for energy-saving and thermal insulation in the building.
Observation of damage caused by major earthquake events over the past decades has shown that structural collapse of unreinforced masonry (URM) buildings is common [
11]. In-situ testing of URM walls was conducted to explore the effects of as-built wall boundary conditions on its out-of-plane strength [
12]. In-plane behavior of cavity masonry infills and strengthening with textile reinforced mortar was studied by Akhoundi [
13]. Salmanpour et al. [
14] carried out a state-of-the-art review of experimental and analytical studies on the deformation capacity of unreinforced masonry walls subjected to in-plane loading. The ultimate deformation capacity was identified as the most important parameter in seismic design and assessment, yet our current state of knowledge on the deformation capacity of structural masonry is limited. It was also argued that the available experimental data display substantial scatter and do not allow establishing a rational value of the deformation capacity of masonry structures based on such experimental data alone. Moreover, reliable and practical analytical models for the force-deformation relationship of structural masonry are yet to be established. Not only are existing finite element models too complex for engineering practice, they also suffer from numerical instabilities in the post-peak regime. It was concluded that we need more experimental tests and robust mechanical models that can capture the load-deformation behavior of structural masonry.
Clearly, there is still a dearth of information in the open literature on how the shape and layout of the ties, the thickness of the insulating layer, and axial compression stress influence the aseismic capability of cavity masonry walls. Moreover, whether the inner and outer leaves of cast-in-situ masonry cavity walls can work in coordination has not been duly investigated. Despite that the in-plane seismic behavior of cast-in-situ masonry cavity walls is of paramount importance, it still needs to be explored and quantified.
The present study aims at acquiring an insight into the cyclic behavior of cast-in-situ masonry cavity walls using quasi-static loading. Thirteen cast-in-situ masonry cavity walls and one solid wall were subjected to combined axial and quasi-static horizontal loads. The failure modes and lateral displacement hysteretic diagrams are presented and discussed. The possibility of using simplified models to estimate the ultimate load capacity of cast-in-situ masonry cavity walls was explored, and comparison with experimental results was carried out. Finally, the seismic performance of cavity walls was assessed, and a parametric study on the effects of the tie shape, tie layout, thickness of the insulating layer, and axial compression was performed. Some problems of the shear capacity and failure mechanisms of cast-in-situ masonry cavity walls were also analyzed, and a formula to calculate the shear capacity was deduced.
3. Experimental Results
3.1. Test Observations and Crack Patterns
For all tested masonry wall specimens, failure was initiated by horizontal flexural cracks followed by the development of wide, diagonal cracks extending throughout the inner leaves. The behavior of the walls can be characterized by three critical points: formation of flexural crack, the opening of diagonal cracks, and crushing of the bottom corners.
Figure 7 illustrates typical wall cracking patterns at the end of testing for three specimens. The walls exhibited shear failure as first fine diagonal cracks appeared in the inner leaves. As lateral displacement increased, the length of the diagonal cracks increased. At this stage, strains of the vertical reinforcement increased significantly, demonstrating its effective role in bearing tensile flexural stresses, avoiding the uplift of the base of the wall. With increasing lateral displacements, easily detectable diagonal cracks developed in mortar joints.
During the displacement-controlled cyclic regime, after three cycles at the displacement of 1∆c (about 1.6 mm), first fine diagonal cracks in the inner leaf could be observed, while the width of diagonal cracks reached about 0.4 mm. During the three subsequent cycles at a displacement of 2∆c, the width of the diagonal crack increased to about 1.3 mm. During the three cycles at a displacement of 3∆c, the diagonal crack widened to about 3 mm, and their length also increased. New irregular cracks were observed as the crack opening increased and extended to the diagonal crack. At this stage, the loading had reached a maximum of about 1.5 times the cracking load. During the cycle at a displacement of 4∆c, the diagonal crack continued to widen to about 5 mm, and diagonal cracks in the inner and outer leaf emerged. After the cycle at a displacement of 5∆c, the load began to decline. Eventually, during the cycle at a displacement of 8∆c, the carrying capacity decreased below 85% of the ultimate load, which was considered a failure.
3.2. Load Versus Displacement Response
The critical loads and corresponding displacements of the specimens are reported in
Table 3, where
Pc and
Pu indicate the cracking load and ultimate load, respectively. ∆
c, ∆
u, and ∆0.85 indicate displacements corresponding to the cracking load, ultimate load, and displacement when the load decreases to 85% of the ultimate load, respectively.
The cracking loads of walls WH83-120-1 and WH64-120-1 were 458 and 454 kN, respectively, while the corresponding ultimate loads were 559 and 540 kN. The rectangular ties were replaced with Z-shaped ties, thus increasing the cracking loads and ultimate loads of wall WZ83-120-1 by 64 and 102 kN, respectively. However, the cracking and ultimate loads of wall WZ64-120-1 decreased by 32 and 37 kN.
The cracking loads of walls WH84-100-1 and WH84-120-1 were 484 and 452 kN, with ultimate loads of 629 and 532 kN, respectively. The vertical spacing of ties was then decreased by 100 mm. Consequently, the cracking and ultimate loads of wall WH83-100-1 increased by 69 and 80 kN, respectively, while that of wall WH83-120-1 increased by 6 and 27 kN, respectively. The horizontal spacing of ties was then decreased by 200 mm. This led to increasing the cracking loads of wall WH64-100-1 by 24 and 80 kN, and an ultimate load decrease of 2 kN. The cracking and ultimate loads of wall WH64-120-1 increased by 2 and 8 kN, respectively.
The shape and layout of ties had a negligible effect on the shear strength of the cast-in-situ masonry cavity walls because the ties behaved as a flexible connection and had limited capacity to coordinate the inner and outer leaves before the failure of the wall specimens. However, the ties could prevent collapsing after the walls had cracked severely.
The cracking and ultimate loads of wall WH84-100-1 were 484 and 629 kN, respectively (
Figure 8a). The walls had similar dimensions and reinforcement details, but the thickness of the insulating layer was varied. When this thickness increased from 100 mm to 120 mm, the cracking and ultimate loads declined by about 32 and 96 kN, respectively. As shown in
Figure 8b, the cracking and ultimate loads of wall WH83-80-1 were 483 and 612 kN, respectively. The cracking and ultimate loads of wall WH83-100-1 increased by 70 and 93 kN, respectively, while that of wall WH83-100-1 decreased by 25 and 53 kN, respectively. The corresponding cracking and ultimate loads of wall WH64-80-1 were 428 and 563 kN, respectively (
Figure 8c), while that of wall WH64-100-1 increased by 80 and 64 kN, respectively. The cracking load of wall WH64-120-1 increased by 26 kN, and the ultimate load of wall WH64-120-1 decreased by 23 kN. The thickness of the insulating layer generally had a slightly negative influence on the wall shear strength. This is likely because the linear stiffness of the RC coupling beams connecting the inner and outer leaf decreased, and the coordination performance of inner and outer leaf degraded, imposing a negative effect on shear strength.
As shown in
Figure 9, the axial compression stress had a positive influence on the shear strength. The performance of wall specimens having similar dimensions and reinforcement details under varying levels of axial compression stress was compared. The cracking and ultimate loads of wall WH83-120-0.3 were 278 and 356 kN, respectively. When the axial compression stress was increased from 0.3 MPa to 0.5 MPa, 0.7 MPa, and 1.0 MPa, the cracking load increased by about 23.0%, 40.3%, and 64.7%, respectively, while the ultimate load increased by 11.8%, 28.9%, and 57.0%, respectively. An increase in axial compression stress delayed the initiation of cracks until larger lateral force was applied. A larger lateral force was required to exceed the compressive field resulting from the larger axial load, and the compressive field must first be overcome before cracking can initiate, as explained by principal stresses. However, ductility indicators declined with increased axial compression stress, and the failure mode became more brittle. Therefore, it is recommended that the axial compression stress should not exceed 1.0 MPa.
3.3. Inner and Outer Leaves Coordination Performance
The load-displacement curves between the inner and outer leaves are shown in
Figure 10. For all specimens, the displacements between the inner and outer leaves were nearly zero before the wall cracked and were less than 2 mm nearing the ultimate load. This indicates that the inner and outer leaves could work in coordination. The relative displacements for the thirteen walls are summarized in
Table 4, where
δ is the maximum displacement between the inner and outer leaves and ∆ is the maximum displacement of the cast-in-situ masonry cavity wall. The ratio
δ/∆ was about 0.25–0.58. The value of
δ for walls WH83-120-1 and WH64-120-1 was 8.0 and 7.8 mm, and their
δ/∆ was 0.58 and 0.52, respectively.
Rectangular ties were replaced by Z-shape ties. Accordingly, the δ of walls WZ83-120-1 and WZ64-120-1 was 9.0 and 8.0 mm, while their δ/∆ values were 0.56 and 0.55, respectively. Likewise, the δ of walls WH84-100-1 and WH84-120-1 was 6.4 and 7.1 mm, and their δ/∆ was 0.47 and 0.51, respectively. The vertical spacing of ties was subsequently decreased by 100 mm. Hence, δ of walls WH83-100-1 and WH83-120-1 was 6.4 and 8.0 mm, while their calculated δ/∆ values were 0.40 and 0.58, respectively. The horizontal spacing of the ties was later decreased by 200 mm. Thus, the δ of walls WH64-100-1 and WH64-120-1 was 4.9 and 7.8 mm, and their δ/∆ values were 0.33 and 0.52, respectively. Generally, the shape and layout of the ties had a slight influence on the coordination work performance of the inner and outer leaves.
As shown in
Figure 11a, the ratio of maximum displacement of the inner to that of the outer leaves over the maximum displacement for the cast-in-situ masonry cavity wall WH84-100-1 was 0.47. The wall specimens had similar dimensions and reinforcement details, but the thickness of insulating layer was increased from 100 mm to 120 mm, making the
δ/∆ value increase by 8.5%.
Figure 11b shows that the
δ/∆ of wall WH83-80-1 was 0.40. When the thickness of the insulating layer was increased from 80 to 100 and 120 mm, the
δ/∆ value increased by 0% and 45%, respectively. Likewise,
δ/∆ of wall WH64-80-1 was 0.34 (
Figure 11c). When the thickness of the insulating layer was increased from 80 to 100 and 120 mm,
δ/∆ increased by 3% and 53%, respectively. It was concluded that
δ/∆ increased with increasing thickness of the insulating layer, while coordination work performance of the walls declined.
Figure 12 shows that
δ/∆ of wall WH83-120-0.3 was 0.27. The performance of the wall specimens having similar dimensions and reinforcement details subjected to varying levels of axial compression stress were compared. When the axial compression stress was increased from 0.3 MPa to 0.5 MPa, 0.7 MPa, and 1.0 MPa,
δ/∆ was 0.36, 0.25, and 0.58, respectively. The
δ/∆ decreased as the axial compression stresses decreased, and the coordination work performance of the walls increased. The axial compression stress generally had a negative influence on the cooperation work performance of inner and outer leaves.
3.4. Hysteretic Loops and Envelope Curves
The hysteretic loops under quasi-static loading were spindle-like. Good aseismic behavior is demonstrated in
Figure 13. The difference of hysteretic loops of the cast-in-situ masonry cavity walls and that of a solid wall was not significant. The hysteretic loops of all walls, which were shuttle shapes, were full. This indicates that the cast-in-situ insulating layer can improve the collaborative performance of the inner and outer leaves. The cast-in-situ masonry cavity walls have desirable ductility and energy dissipative capacity. The envelope curves of the wall specimens can be divided into three stages: elastic stage, elastic-plastic stage, and failure stage, as displayed in
Figure 14. For the convenience of comparative analysis, the envelope curves are simplified as a tri-linear substitute model, as shown in
Figure 15. The slope of the line connecting the cracking point to the origin point was
Kc, where
Kc =
b/a; the slope of the line connecting the cracking point to the ultimate load point is
K1, where
K1 = (1 −
b)/(1 −
a); the slope of the line connecting the ultimate load point to the failure point is
K2, where
K2 = (1 − 0.85)/(
c − 1).
Kc,
K1, and
K2 of the walls are summarized in
Table 5.
Kc of the cast-in-situ masonry cavity walls was about 2.03–3.75, and the ratio of
Kc of the cast-in-situ masonry cavity walls to that of the solid wall was in the range of 0.86 to 1.8. Compared with the solid wall, the initial stiffness of cast-in-situ masonry cavity walls did not decrease significantly, and the degenerative process of the stiffness of the cast-in-situ masonry cavity walls was delayed to some degree. This indicates that the cast-in-situ insulating layers contributed to resisting stiffness degradation.
3.5. Ductility Factors and Energy Dissipation
Figure 16 outlines the method of determining the ductility factor,
, which is the ratio of the displacement corresponding to the ultimate load (∆
u) and the equivalent yield displacement (∆
y).
The values of the ductility factor for cast-in-situ masonry cavity walls are summarized in
Table 6 and were in the range of 2.86–4.17, with an average value of 3.4. The ductility factor of the solid wall was 3.38, which is comparable to the average ductility factor for cast-in-situ masonry cavity walls. The shape and layout of ties, the thickness of insulating layers, and axial compression stress had a slight influence on the ductility factor.
Energy dissipation is an important parameter in modeling the cyclic response of the cast-in-situ masonry cavity walls and for the evaluation of its seismic performance. The energy that is dissipated at each loading cycle,
Ediss, was obtained by numerically integrating the force-displacement hysteretic loop. To have an objective measure of the dissipated energy due to the influence of lateral strength on calculations, the normalized dissipated energy by the elastic energy absorption of the equivalent elastic-plastic model was adopted. The energy dissipation coefficients of the cast-in-situ masonry cavity walls ranged between 1.07–1.42, with an average value of 1.25, as indicated in
Table 7. Compared to that of a solid wall, the energy dissipation coefficients of the cast-in-situ masonry cavity walls did not exhibit significant decay. Hence, the energy dissipation capacity of the cast-in-situ masonry cavity walls could meet the design requirements.
3.6. Shear Capacity and Failure Mechanism
The load-displacement curves were initially linear during the early stage of the load test. The vertical and horizontal mortar seams started cracking at the same time and then cracks developed diagonally with a ladder-like distribution. The principal strain theory, which assumes that failure occurs when the maximum strain becomes equal to the strain at yield point, could explain this phenomenon. However, the cast-in-situ masonry cavity walls had very high shear strength after cracking, and the sheer load-carrying capacity continued to increase. In fact, the cast-in-situ masonry cavity walls were damaged after cracking not because of tension, but due to slippage and movement of the horizontal mortar seams. The principal strain theory failed to explain this phenomenon. The walls were destroyed when the bond strength and friction coefficients of the horizontal mortar seams declined substantially. This can be explained via the shear-friction strength theory. The characteristic shear strength is given by [
16]:
where
is the characteristic initial shear strength under zero compressive stress,
is the design compressive stress perpendicular to the shear in the member at the level under consideration, using the appropriate load combination based on the average vertical stress over the compressed part of the wall that is providing shear resistance.
where
is the partial factor for masonry. The design value of the shear resistance is given by:
where
is the design value of the shear resistance of unreinforced masonry;
is the design value of a constructional column and,
where
is the design value of the shear strength of masonry;
is the thickness of the wall resisting the shear;
is the length of the compressed part of the wall, ignoring any part of the wall that is in tension.
is given by [
17]:
where
is 0.18/
,
is the partial factor;
is the adjustment factor;
is the ratio of longitudinal reinforcement;
is the concrete crushing strength;
is the concrete compressive stress at the centroidal axis due to axial loading;
is the smallest width of the cross-section in the tensile area;
is the cross-section length.
Experimental testing proved that the outer and inner leaves could work in coordination. Therefore, the beneficial effect of the outer leaf should be considered. The shear strength can be calculated, including the outer and inner leaves by the following expression:
where
is the shear strength of inner leaves;
is the reduction coefficient;
is the shear strength of outer leaves. According to the test,
.
A comparison between the calculated and experimental test values is summarized in
Table 8. The average ratio of calculated value to the test value was 1.08, while the standard deviation was 0.08, and the coefficient of variation was 0.074. Therefore, the developed expression achieved adequate accuracy for predicting the shear strength of the cast-in-situ cavity masonry walls.