GNSS (GPS) Monitoring of Dynamic Deflections of Bridges: Structural Constraints and Metrological Limitations

Abstract

The advent of modern geodetic satellite techniques (GNSS, including GPS) permitted to observe dynamic deflections of bridges, initially of long flexible ones, and more recently of short, essentially stiff bridges with modal frequencies > 1 Hz, and with small SNR (signal-to-noise ratio), even SNR < 1. This was an enormous progress, but not without problems. Apart from monitoring results consistent with structural models, experimental data and serviceability criteria, there exist some apparently unexplained cases of stiff bridges for which there have been claimed apparent dynamic deflections too large for common healthy structures. Summarizing previous experience, this article: (i) discusses structural constraints, experimental evidence, and serviceability limits of bridges as constraints to GNSS monitoring; (ii) examines a representative case of careful monitoring of a reinforced concrete road bridge with reported excessive dynamic deflections; and (iii) explains such deflections as a result of a double process generated by large reflective surfaces of passing vehicles near the antenna; first corruption/distortion of the satellite signal because of high-frequency dynamic multipath, and second, shadowing of some satellites; this last effect leads to a modified observations system and to instantaneously changed coordinates and deflections. In order to recognize and avoid such bias in GNSS monitoring, a strategy based on practical rules and structural constraints is presented.

1. Introduction

Deformations of the deck of bridges, in the form of deflections from their original surface, produces discomfort, even hazard of collapse, and are among the parameters characterizing bridge performance. Deflections can be static (when a load is not moving/changing in time, for example, vehicles stopped on a bridge), semi-static (when a load is changing smoothly, but is stable for an interval exceeding the natural frequency of the structure) or dynamic (when the load is changing rapidly, for example, due to wind or traffic).

Dynamic bridge deck deformation was highlighted by the famous collapse of the Tacoma Narrows Bridge in USA in the 1940s [1], and more recently by the impressive lateral deflections of the Millennium Bridge in London during its opening, during the first day of the new millennium [2]. About 25 years ago there have been published the first studies of measurement of dynamic deflections of bridges using vision-based techniques [3] and satellite geodetic techniques-GPS [4]. This was a real breakthrough, because till then, for lack of the necessary measuring technology, it was extremely difficult, if not impossible, to measure static and especially dynamic bridge deflections, mostly for long bridges.

In fact, till recently, it was possible to measure static deflections of bridges using conventional survey techniques, either through leveling along the deck of the bridge, or through observations at distances of usually up to a few hundred meters from stations not lying on the bridge (for example from the banks of a river or from nearby islets) for distances of up to several hundred meters. On the contrary, the main possibility to measure dynamic deflections at the midspan of a bridge was to use LVDT extensometers on scaffoldings at the bottom of the bridge deck [5,6]). This last technique was, however, possible for bridges in favorable conditions, for example, over a dry riverbed and with short clearance (distance of the deck from the ground bottom). For this reason, deflections were mainly based on model predictions (e.g., [7]). Concerning long, flexible bridges, the problem was more complex because wind tends to produce large deflections (Figure 1). In such cases, analysis of scaled models in wind tunnels is a solution, but detailed analysis of wind effects on long bridges requires high-pressure, high Reynolds number wind tunnels, are very few (for instance, in Princeton University, USA; [8]). For these reasons, deflections of bridges of different types due to dynamic loads remained rather unknown, and regulations for bridge performance all around the world relied on model predictions and on certain empirical criteria (e.g., AASHTO 1997 [9]).

In the last 20 years, however, GPS, known as GNSS after the advent of GLONASS and of other satellite positioning systems in the last decade, has been used to measure dynamic deflections of long span bridges [4,10,11] (Figure 1); in some cases permanent monitoring systems including geodetic sensors have been adopted [12]. Geodetic techniques, usually combined with accelerometers, have been recently used to cover short span, stiff bridges (main natural frequency f > 1 Hz) with deflections of a few mm also [13,14,15,16,17]. In a few cases, however, combination of GNSS with RTS (robotic theodolite or robotic total station) have permitted to recognize that the GPS (currently GNSS) signal may be corrupted, usually beyond repair [18].

In addition, as is explained in Section 4 below, there has been reported some cases of short, stiff bridges for which excessive, non-realistic dynamic deflections based on GNSS monitoring have been claimed. This indicates that geodetic monitoring of bridges, especially of short, stiff bridges has certain limitations, and ignoring these limitations may lead to pitfalls. Focusing to this problem, the aim of this paper is (i) to examine certain constraints in the output and the applicability of GNSS bridge monitoring imposed by structural data; (ii) recognize certain pitfalls of the GNSS monitoring, mostly in form of apparent excessive deflections of stiff bridges; and (iii) explain the causes of such pitfalls and (iv) propose some practical rules to avoid them.

These results are very important because short span bridges represent the striking majority of highway and railroad bridges all over the world, little attention is usually paid to their structural health, the percentage of damage in relatively high (cf. [19]) and the problem of pitfalls in the estimations of dynamic deflections of stiff bridges has hardly been understood.

2. Structural Constraints in Dynamic Deflections of Bridges

2.1. Evidence from Regulations and Codes

Depending on its geometry, type and structural health, each bridge has dynamic characteristics falling within specific ranges. For example, adopting the approximate formula of Bachmann et al. [20], the fundamental frequency f of a short, stiff concrete bridge is defined by the formula

f = 100/L

(1)

where L the is span length in meters, f in Hz.

Serviceability criteria incorporated in various Structure Codes provide also a priori structural constraints to bridge dynamics and especially deflections. The aim of these criteria is to ensure properly functioning bridges, with limited deflections. If vertical deflections exceed specified values, excessive vibrations of the bridge are expected, giving the feeling of a vehicle running through an anomalous or vibrating road surface, even with a road bump. To exclude this possibility, the typical AASHTO (1997) [9] serviceability criterium specifies that the deflection d of a bridge and its Length L are related with Equation (2)

d < L/k

(2)

where k is a parameter characterizing various types of bridges. For example, for a 20 m-long bridge made of reinforced concrete, k = 800 or 1000. This means for example that the natural frequency of a healthy, 20 m-long concrete bridge is of the order of 5 Hz, and its maximum acceptable deflection is 2 cm. A smaller fundamental frequency and/or a higher deflection indicate either a poor construction or a damaged structure. The poor performance of such a structure may be recognized by users, while signs of damage (cracks, etc.) will be visible.

2.2. Evidence from Field Data

A study of the literature permitted to identify a few cases of stiff bridges with an opening (span) of 20–60 m, of different types, the dynamic deflections of which have been measured using different types of sensors (direct contact/LVDT, radar interferometry and robotic total station (RTS), but not GNSS). This evidence was then used to provide constraints to GNSS measurements.

Data are summarized in

Table 1. Deflection measurements of stiff bridges (not based on GNSS).

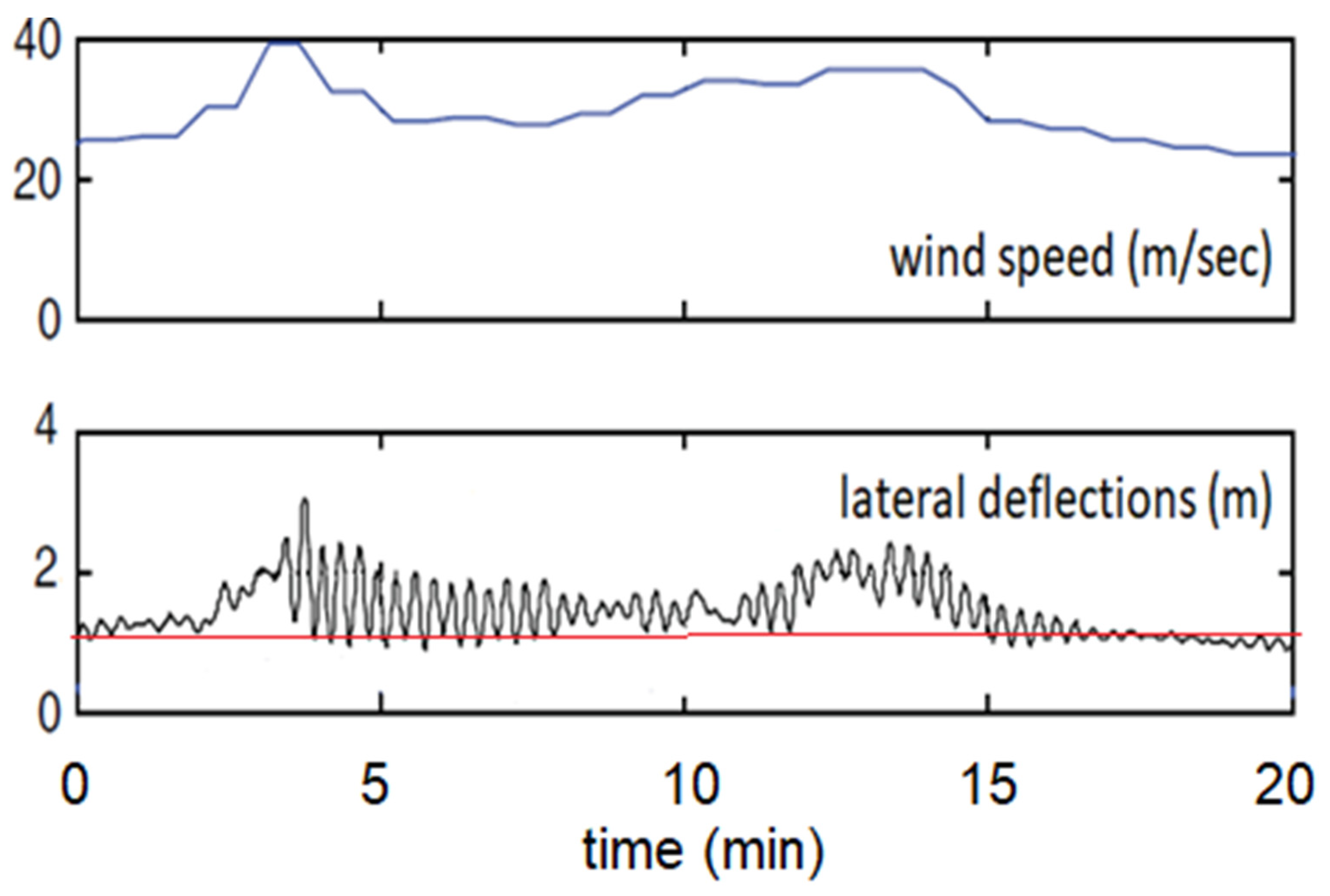
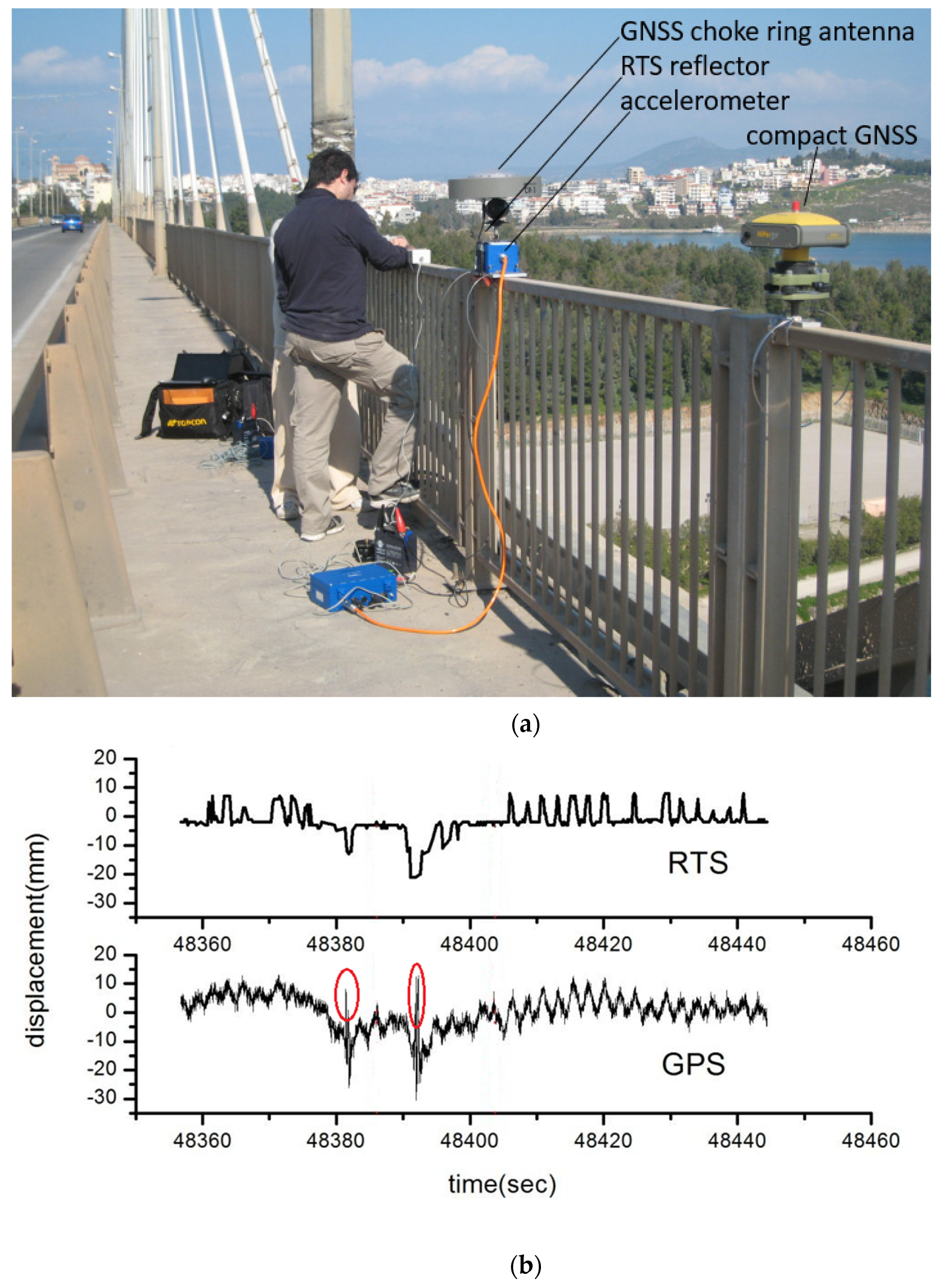
Bridge	Span (L) (m)	Vertical Deflection (d), (mm)	Type of Measurement	Loading	Ref.
timber deck train bridge	24	<4	LVDT	passing train	[6]
motorway multi-span pre-stressed RC bridge	~20	<3	Radar interferometry	cars and trucks	[22]
Historic metallic train bridge (GR)	30	6	robotic total station (RTS)	passing train	[16]
Pedestrian metallic, three-span truss bridge (GR)	41	<6	robotic total station (RTS)	coordinated jumping to resonance	[14]
three-span RC bridge	62	<3	Radar interferometry	traffic	[23]
five-span pre-stressed motorway bridge	24	~300 (at failure)	LVDT	bent to failure	[21]

and indicate that in none of the bridges examined deflections above 1 cm were observed. The only exception is a reinforced concrete bridge in Kiruna, Sweden, which was subject to controlled loading till failure. In this case, total failure occurred when the vertical deflection reached approximately 300 mm [21]. These results indicate that deflections of structurally healthy, stiff bridges can hardly exceed 1 cm in amplitude, and deflections of the order of tens of centimeters are associated with structural damage.

2.3. Modal Frequencies, Resonance, and Deflections

A basic rule in mechanics is that the response of a structure to loading (for example, the amplitude of oscillation, etc.) becomes important in the case of resonance, i.e., if the frequency of excitation tends to the natural frequency of a structure. Non-resonant loadings have limited effects in structures. This effect was highlighted in the case of the 1985 Mexico earthquake. This high-magnitude (M8.0) earthquake produced both long-period and short-period waves, but short-period waves were rapidly attenuated away from the fault, and Mexico City, at a distance of about 350 km, was affected by long-period waves only. These waves had enough energy because of the large magnitude of the shock, and produced resonance to tall, long-period buildings, many of which were seriously damaged. On the contrary, nearby low-rise buildings (short-period structures), even of poor construction, suffered no damage because they were insensitive to long period seismic waves.

This principle can be extrapolated to bridges.

Bridges are rather complicated structures and are usually characterized by several modal frequencies. A certain type of dynamic loading, depending on its frequency, may excite a specific natural frequency, corresponding to a specific modal shape. First and second modes have typically higher energy and respond with dynamic deformation of relatively high amplitude (Figure 1). On the contrary, the contribution of lower modes in dynamic deformation is typically less significant (usually a small percentage of that of high modes).

A short, stiff bridge (natural frequency f > 1 Hz) is insensitive to long-period excitations (for example, wind gusts flowing say every 30 s, the likely reason of secondary oscillations in Figure 1) and is only sensitive to dynamic loads with frequencies close to its natural frequency.

A structurally healthy, long, flexible bridge (essentially its deck), on the other hand, is typically sensitive to long period loading only. A characteristic example is the Evripos suspension bridge in Chalkis, Greece. Characteristic modal frequencies of this bridge which has a main opening of about 400 m are shown in

Table 2. Characteristic modal frequencies of the Evripos suspension Bridge, Greece. Based on [24].

Mode 1	Mode 2	Mode 11
f1 = 0.36 Hz	f2 = 0.39 Hz	f3 = 0.94 Hz
excited by traffic	excited by traffic	excited by earthquakes

. These natural frequencies describe the response of the bridge to various excitations. High-amplitude, high-frequency oscillations are unlikely for the deck of such a bridge. Since this bridge is located in an earthquake-prone area, certain earthquakes selectively exited a lower (11th) modal frequency ([24], Table 2) due to resonance, and to a lower degree the 1st mode, but they produced no harm to the deck because the 11th mode absorbs very little energy. On the contrary, traffic load and wind tend to excite the two higher modes and produce long-period oscillations, as is derived from monitoring using GNSS and RTS (Figure 2b), and in extreme cases they may represent a threat for damage.

3. Bridge Type, SNR and Multipath in Geodetic Deflection Measurements

3.1. Typical GPS/GNSS Accuracies

GPS (GNSS) is known to permit coordinate differences even of sub-mm level. Still, this precision is confined to static measurements, deriving from a kind of averaging coordinates of survey points (in fact of antennas) for relatively long intervals (static analysis). Estimation of the movement (including oscillations) of a point in which a GNSS antenna is clamped, is based on kinematic analysis techniques, i.e., assuming instantaneous changes of coordinates. High accuracy measurement of moving antennas is derived from the comparison of the recordings to the moving antenna relative to a nearby fixed reference GNSS antenna/receiver (differential kinematic solution) or to a large number of antenna/receivers spread over a large region (Precise Point positioning, PPP-technique). The sampling rate of GPS/GNSS was in the past 1 Hz, but it gradually reached 10 Hz and even climbed to 100 Hz [15], while the accuracy of isolated measurements of displacements/oscillations with frequencies up to 4 Hz is better than 20 mm for simple differential and for PPP post-processing techniques [25]. These accuracies are of course possible under normal conditions, when measurements are not affected by specific types of systematic errors described below. Important to notice that accuracy is different from precision. Accuracy means the difference of an estimate from its “true” value, while precision means how various estimates are close to their mean value.

3.2. Long, Flexible Bridges

The accuracy and versatility of GPS encouraged its use in bridge dynamics, and the first efforts to measure dynamic deflections were made for long-span bridges; this is because of their importance and because they were expected to be characterized by long-period, large-amplitude deflections (see above). Measured dynamic deflections of long bridges were found of the order of 10–100 cm (Figure 1), i.e., of a level much higher than the corresponding measurement noise. In such cases the SNR (signal-to-noise ratio) of dynamic displacements remains typically high for Geodesy, SNR > 1, and permits safe results. The excellent results of geodetic monitoring permitted to establish GPS as a valuable tool for monitoring of long, flexible bridges [4,10,11].

It must be noticed that very large-amplitude deflections as those described in Figure 1 do not cause any damage to modern healthy, flexible bridges, but they may cause some discomfort to users and perhaps a risk of loss of control of vehicles. For this reason, in the case of real-time monitoring, the amplitude of deflections can be used as criterion for interruption of circulation.

3.3. Short, Stiff Bridges

High-rate (10 Hz or higher, up to 100 Hz [15]) GNSS monitoring was recently expanded to short-span bridges. These bridges are usually stiff (f > 1 Hz), with small deflections, ranging from submillimeter level (c.f. [26], so that geodetic monitoring is not possible) to a level of a few mm or cm (see also Table 2). In such cases, typical GNSS measurement and analysis techniques lead to a SNR < 1, and hence to imprecise results. More refined geodetic analysis is, however, possible only in combination with other sensors (for example GNSS combined with RTS and accelerometers) and specific filtering (denoising) techniques; an example is shown in Figure 3; see also Figure 2 in [13].

3.4. The Threat of Dynamic Multipath

Multipath is a threat for all radio-type waves, including those of GNSS. This problem arises from the fact that the signal from a satellite may not directly arrive at a GNSS antenna (in most cases combined with a receiver to form a compact GNSS unit; see Figure 2a), but it is first reflected to a certain surface, so that an increased distance between satellite and antenna is obtained.

Typical multipath represents a static or semi-static effect, because the satellite constellations above each site gradually change (satellite orbits are of the order of 24 h). In long bridges conventional multipath is usually produced by cables, producing secondary reflections to the signal arriving at a GNSS antenna. Specific types of antennas, like the one shown in Figure 2a (“chock ring antenna”) reduce this effect. Exclusion of low-elevation satellites (i.e., adopting a “mask angle”, i.e., an angle of 15°, to exclude all satellites at an elevation smaller than 15°, in analogy to astronomy) is another technique to suppress conventional multipath. Some computational techniques to mitigate multipath have also been proposed [27].

About 20 years ago, Wieser and Brunner [18], who introduced bridge monitoring using both GPS and RTS, noticed unrealistic apparent GPS-derived bridge deflections, of the order of about 10 cm (Figure 4) and assigned them to multipath (reflections of satellite signal to the nearby bridge cables. This noise, however, is a rather long-period effect (shifting of the base line at around 8:08 by about 10 cm). However, a closer look indicates an amplification of the RTS deflection signal in GPS data, and this represents a high-frequency effect.

Corruption of the GNSS signal had been observed during the monitoring of a train bridge using both RTS and GNSS [16], and this inspired systematic studies of this type of noise. These studies included experiments with GNSS antennas on stable ground next to the train tracks, mimicking bridge monitoring. The results were surprising, for the satellite signal was corrupted during the passage of trains, and the peaks correlated with the number of wagons and their reflective surfaces; spurious peaks could even be used as time stamping for the passage of trains. Further analysis of this effect, indicated that the signal corruption derived from two effects [28], as is explained in Figure 5.

First, shadowing of some satellites because of passing vehicles, so that the geometry of the observations system was instantaneously changed, and this highly influenced computed coordinates and computed instantaneous deflections. In favorable cases, this effect may be treated in a simple way: temporarily shadowed satellites are excluded from processing of the whole time series of observations.

Second, the signal of some of the satellites before it arrives at the GNSS antenna reflects to a passing reflective surface of a vehicle and produces a corrupted signal during the passage of the vehicle; this instantaneous effect represents a dynamic multipath effect, different from the long-period conventional multipath.

Unfortunately, in most cases it is not known with certainty which satellites are corrupted, and a possible remedy is to exclude possibly infected satellites, especially those in low altitude.

4. Reported Large Deflections of Stiff, Structurally Healthy Bridges

Although structural constraints predict small deflections in stiff bridges (Table 1), there exist certain reports of abnormally large GNSS-derived deflections. Structural damage has usually been claimed as an explanation, but no signs of such damage were found (cracks in concrete, etc.), nor any sense of dysfunction by users of the bridges has been reported.

An example is the results of GPS monitoring of the Juarez Bridge, in Culiacan, Mexico [30]. This is a typical reinforced concrete road bridge, with openings of 20 m supported by beams on piers and two lanes per direction. Measurements were made in seven consecutive days, during specific time intervals, at traffic rush hours in order to identify the response of the bridge to the traffic load. Six GPS compact antenna/receivers were mounted on poles about 2.0 m high clamped on stiff metal railings at the two sides of the bridge, including its midspan. Measurements were collected with a sampling rate of 1 Hz and were probably limited to GPS satellites only, while a low cut-off (mask) angle of 10° was adopted (i.e., accepting satellites at zenithal angles of 0–80° around each antenna). As a consequence, certain stationary or moving reflecting surfaces (passing vehicles) at an elevation slightly above the antennas were influencing calculations. The analysis was made in reference to stations in stable ground, using high precision software. The output was instantaneous (1 Hz) changing coordinates in three axes, forming an angle of approximately 40° with the road axis. These results indicate apparent displacements up to tens of cm in the horizontal and vertical axis. After removing the long-period component of satellite signal, the authors argued that they recorded dynamic deflections of several cm in both the horizontal and vertical axes. In some cases, vertical apparent deflections up to 25 cm in the midspan were recorded. Deflections were not confined to the mid-span, but they were also observed at stations above piers of the bridge (

Table 3. Maximum vertical dynamic displacements of the Juarez bridge. Data based on Figure 9 in [30]. Measurements were collected from 6 GPS instruments during 21 sessions, which are divided in this Table in three sets of seven sessions each, with inferred quasi-similar satellite constellations. Four instruments were set above bridge piers (and are typically expected to show no deflections) and two at the midspan. Large apparent deflections were reported, up to 13 cm above piers and up to 25 cm in the midspan. This order of apparent deflections is much higher than those observed on other bridges and is expected only at bridge destruction level (cf. Table 1).

Measurement session		1	4	7	10	13	16	19
Max deflection(cm)	midspan	4	9	21	5	9	8	5
	pier	5	4	7	5	4	4	3
session		2	5	8	11	14	17	20
Max deflection(cm)	midspan	24	9	14	5	7	18	8
	pier	13	4	5	5	5	5	8
session		3	6	9	12	15	18	21
Max deflection(cm)	midspan	25	20	11	4	5	13	7
	pier	12	4	5	3	4	8	4

). The authors were surprised with these results, noticed that the deflections were exceeding the serviceability limits of this bridge, and although they found no signs of damage, they explained them as results of a possible unnoticed structural damage.

5. Discussion

5.1. Contrasts between Observations and Structural Predictions

Table 1 indicates that measurements of dynamic deflections of stiff bridges, including bridges of reinforced concrete, using different types of sensors (LVDT extensometers, radar interferometry, and robotic total stations (RTS) led to max values of vertical deflections of the order of a few mm. In some of these cases, combined GNSS and RTS measurements revealed that carefully collected and analyzed GNSS data are consistent with those derived using RTS (e.g., [14]), but in some cases the output of GNSS is contaminated by serious errors (Figure 4). A deflection of the order of 300 mm was recorded only for a bridge just prior to failure, in a catastrophic experiment (Table 1).

On the other hand, GNSS measurements of dynamic deflections of various types of bridges, disproportional to the predictions of various codes, have been made in various parts of the world, and some of these results have been published in international journals. This makes the study of the Juarez bridge representative of several other cases, and worthy of discussion, especially because measurements were made with much care.

The AASTHO [9] and other regulations predict maximum permissible dynamic deflections up to 2.0–2.5 cm for this bridge, but reported deflections were up to about one order of magnitude higher (up to 25 cm) for the three axes (Table 3). Still, no evidence of discomfort to the users, nor signs of damage (cracks, unstable foundations etc.) were reported. Computed horizontal deflections of a few cm in this bridge may be explained as secondary oscillations of the poles on which the GPS antenna and receiver units were mounted. Hence the main problem is the inferred vertical deflections, reaching 10–25 cm at the midspan and at least 10 cm above the piers of the bridge (Table 3). Under certain conditions, heavy loads may produce dynamic subsidence in piers of bridges of sub-millimeter to millimeter-scale [16]. Hence, reported vertical deflections above piers in the Juarez bridge (up to 13 cm) can only reflect bias.

A last argument: Dynamic deflections of short-span (20–30 m long) bridges above the threshold of a few cm are visible by naked eye, can be easily video-recorded from a nearby position (for an example see [31]), produce a sense of discomfort, and occasionally of fear to pedestrians and car drivers; they can also be analyzed using a combination of photogrammetric and typical video-processing techniques [32]. In fact, in favorable conditions (good visibility and proximity to the bridge) such techniques can identify and model even micro-vibrations [33,34,35]. Hence a simple control to ambiguous results is possible.

5.2. Searching the Source of the Error in the GNSS Data

The survey of the Juarez Bridge and the analysis of data were made with much care, though with a sampling frequency of 1 Hz, too small for a stiff bridge; hence, the possibility of blunders should be excluded. Furthermore, measurements were made in consecutive days, with the same hourly plan, so that each group of observations was made under a rather uniform, slowly changing constellation of GPS satellites. In addition, the GPS antennas were at an elevation which does not justify offsets such as those of Figure 4 due to conventional multi-path (reflections of satellite signals to nearby buildings before they arrive the antennas), in spite of the fact that a low (10°) cut-off angle was adopted.

Under these conditions, the only possible explanation is a combination of shadowing of some satellites in combination with dynamic multipath, i.e., corruption of the GPS signal by selective reflections to passing vehicles and the low frequency of sampling. Such measuring conditions do not cause systematic effects, i.e., a quasi-steady bias for each group of observations during observation sessions with the same satellite constellation. This is because the geometry and reflectivity of the surfaces of passing vehicles, their distance from the antennas and the velocity of the vehicles are different. For example, a highly reflective surface of a large lorry passing closer to a monitoring antenna with lower velocity is expected to produce maximum bias in all three coordinates. In addition, as Figure 4 indicates, multipath effects may vary considerably only after a few minutes.

It can hence be concluded that transient shadowing of some satellites by vehicles and the associated dynamic multipath are effects critical for monitoring bridges, and they may highly influence the quality of results in low SNR conditions. Distortion of the GNSS signal under these conditions is not easily recognized because it correlates with passing vehicles and it may be assumed that it reflects structural response to dynamic loading. However, such effects are critical in short bridges but minimized at the midspan of major bridges with the deflections as those of Figure 1, for several reasons. (i) In long, flexible bridges deflections are large (cf. Figure 1) and the SNR is usually high, so that the contribution of dynamic multipath is usually small and ignored. (ii) Filtering can remove effects such as the spurious pulses in Figure 2, and even the multipath can be removed using an algorithm such as that proposed by Roberts et al. [27]. (ii) Major bridges allow enough space between an antenna and the top of passing vehicles, so that dynamic multipath and shadowing of satellites are minimized.

6. Strategy for Reliable Bridge Monitoring

There are some simple practical ways to ensure the reliability and significance of monitoring results and minimize pitfalls, especially due to dynamic multipath.

First, a monitoring survey should be planned only after the dynamic characteristics of a study structure are known or obtained as approximate values using rules of various regulations and Codes (see for example Section 2.1).

Second, if possible, there should be made measurements at points with different dynamic behavior, especially points which are expected to have no deflections, for example at the edges of the deck, above pylons, and at points which have maximum deflections, usually at midspans. Alternatively, the same point(s) can be measured, both in intervals of loading and of no loading (mostly traffic), if this is possible. Deflection signal in points/intervals in which no deflections (are expected define the noise level of instruments/analysis (“background noise”), while the signal in points/intervals in which deflections are expected should exceed that noise level in order to document dynamic deflection. This requires of course that sensors have the necessary resolution to record deflections predicted for a specific structure, for example, based on Equations (1) and (2).

Third, different sensors should be combined, for example GNSS and accelerometers, hopefully collocated with RTS (see Figure 2); or at least some control of GNSS data using RTS and other techniques permitting deflection measurements such as radar interferometers [22,23] and optical techniques [2,32,33,34,35] during certain surveys is recommended. In our days, some of these studies can be based even on sensors embedded in smartphones; for example, smartphone accelerometers can easily permit to recognize a strong excitation with high deflections from a weak excitation with smaller deflections (e.g. [36]).

Fourth, GNSS sensors should be mounted on stiff bases (in the simplest of the cases, poles stiffened laterally with tensioned wires) and at elevations ensuring no secondary reflections from passing vehicles to the antennas (see Figure 5).

Fifth, after a conventional analysis of satellite signals leading to dubious peaks, skyplots (projections of tracked satellites on a sky map) just before, during and just after dubious peaks must be examined in order to investigate whether one or more satellites were shadowed by vehicles (see [28], Figure 5). These satellites should be removed from the analysis because transient changes in the geometry of observations (satellites) may modify solutions and give the impression of displacements.

These simple, practical rules, listed not in the order of their significance, are expected to permit safe GNSS bridge monitoring.

7. Conclusions and Summary

Evidence presented in this article indicates that despite the progress and increasing popularity, GNSS monitoring of bridges has some limitations, especially for short, stiff bridges, in which the SNR of geodetic estimates of deflections is low, even SNR < 1. In such cases, GNSS results may lead to excessive apparent semi-static and dynamic deflections of bridges, inconsistent with their overall performance. This is reflected in the contrast between evidence summarized in Table 1 and Table 3. Table 1 indicates that the vertical dynamic deflections of stiff bridges are typically of sub-cm level; a result consistent with various Codes which predict maximum deflections of the order of up to a few cm to satisfy typical serviceability criteria (e.g., AASHTO [9]). Table 1 also indicates that deflections of the order of 20 cm are observed only during destructive tests of stiff bridges. Table 3 on the contrary, deriving from a careful study, indicate deflections of tens of centimeters for a concrete bridge with a span of 20 m and with no visual signs of damage, cracks, etc., and with no sense of discomfort because of high oscillations to passing vehicles. Quasi-similar results have been reported for other stiff bridges as well, but the study of Vazquez et al. [30] is unique because it was made carefully, and because the authors were surprised by their results, for which they could find no explanation other than an unusual structural behavior. Hence the focus of the article was to find an explanation for this problem and propose ways to avoid it.

Systematic field studies and experiments summarized in this study indicate that the source of error for amplified (and perhaps also attenuated) dynamic bridge deflections is a near-field effect, an impact of vehicles with large reflecting surfaces passing close to the antenna. These vehicles influence the received signal in two ways. First, the signal of certain satellites is reflected on passing vehicles before it arrives the GNSS antenna, and this additional distance (multipath), large for the wavelength of a radio signal, produces a bias in the instantaneous coordinates of the antenna and of the computed bridge deflections (see Figure 2b and Figure 5). This represents a dynamic multipath effect, due to a rapidly moving reflecting surface near the antenna, correlating with traffic. Dynamic multipath is different from the quasi-static multipath deriving from reflections from static reflective surfaces, for example, bridge cables, corresponding to long-period noise because of the slow movement of satellites. Second, certain satellites may be instantaneously shadowed by passing vehicles (Figure 5), and hence the observations system (i.e., the set of satellites the signal of which is recorded by the antenna and analyzed) is instantaneously (temporarily) modified; this leads to instantaneous, spurious shifts of the antenna coordinates and to biased antenna (and bridge) deflections.

The main characteristic of these two effects is a high-frequency impact on the instantaneous antenna coordinates and spurious bridge deflections, correlating with intervals during which vehicle with high reflective surfaces (and hence mass) passes next to the antenna. This gives the wrong impression of a causative relationship between high bridge loadings by lorries and high bridge deflections. Since no specific sensors to control bridge loading usually exist (e.g., [37]), certain simple techniques to avoid these types of bias in dynamic deflections (using the pattern of Figure 5) and recognize, even minimized them, were summarized in Section 6. However, once high-frequency deflections of a stiff bridge are contaminated by dynamic multipath, no healing is possible (cf. [16,28]).

This double, high-frequency bias can also be recognized in longer, flexible bridges (Figure 2b). However, in these bridges, the SNR is high, and the bias described above is usually a minor effect, which, in addition, can be easily removed with low-pass filtering of the long-period deflections of flexible bridges (cf. Figure 2b).

Hence, the results of this study are important for all cases of GNSS monitoring, long, flexible bridges which till recently represented the focus of GNSS [29], and short, stiff bridges to which GNSS deflection monitoring has been recently applied, and some of which risk to be recognized as structurally unhealthy because of biased GNSS-derived deflections.