Assessment and Fragility of Byzantine Unreinforced Masonry Towers
Abstract
:1. Introduction
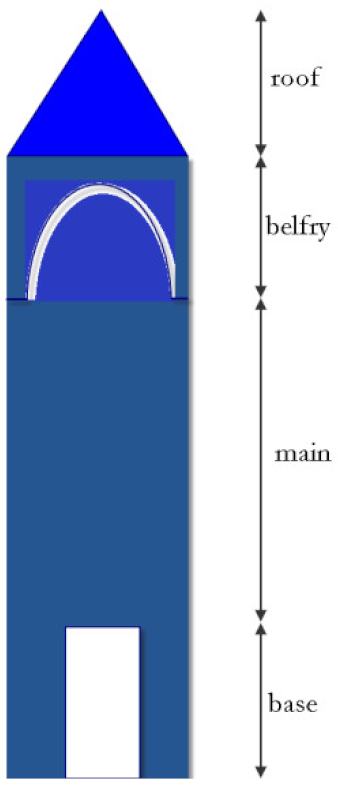
2. Characteristics of the Investigated Bell-Towers
2.1. Architectural Features
2.1.1. Vatopedi Tower
2.1.2. Philotheou Tower
2.1.3. Protaton Tower
2.1.4. Xenophontos Tower
2.1.5. Iveron Tower
2.2. Modal Properties
- The walls’ width is kept constant along the height because variations are considered relatively small;
- The diaphragmatic action of the timber floors and vaults is assumed inactive;
- The mass of the timber floors and vaults is added point-wisely on the URM walls estimating the tributary areas.
3. Collapse Mechanisms of Towers
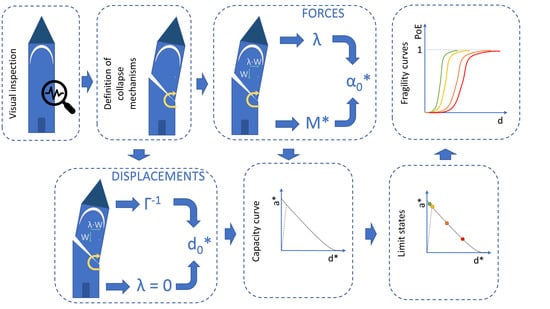
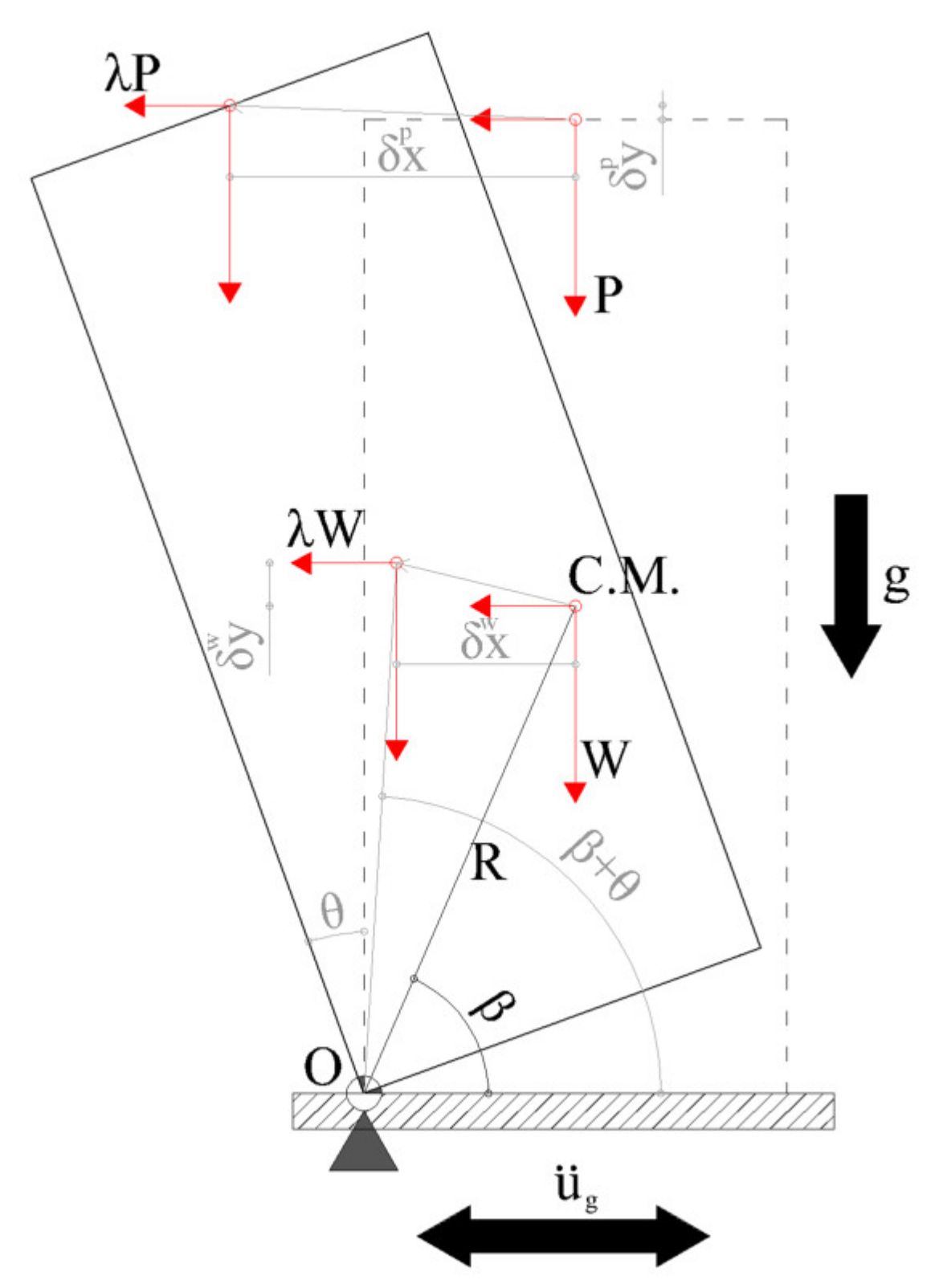
4. Assessment Based on Limit Analysis
4.1. Overturning [1 - ANA]
4.2. Separation [2 - APO]
- is increased by a specified step;
- Vertical stresses in the contact areas are estimated;
- Friction forces are estimated;
- The static forces safety factor is estimated;
- If is negative the specified step is decreased to reach a balance ( = 0).
4.3. Diagonal Cracking [3 - DR]
4.4. Dislocation of the Belfry [4 - ΚOR]
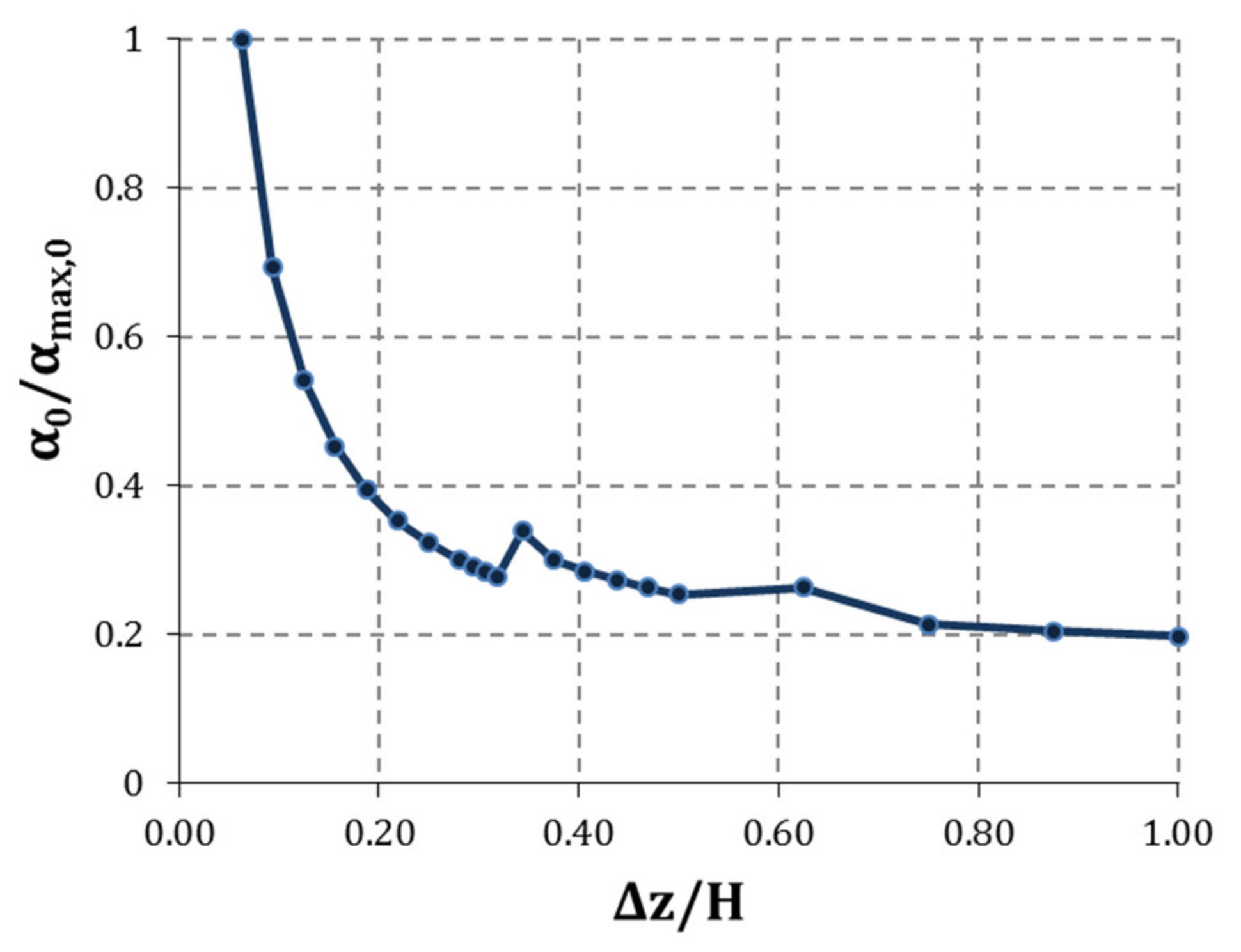
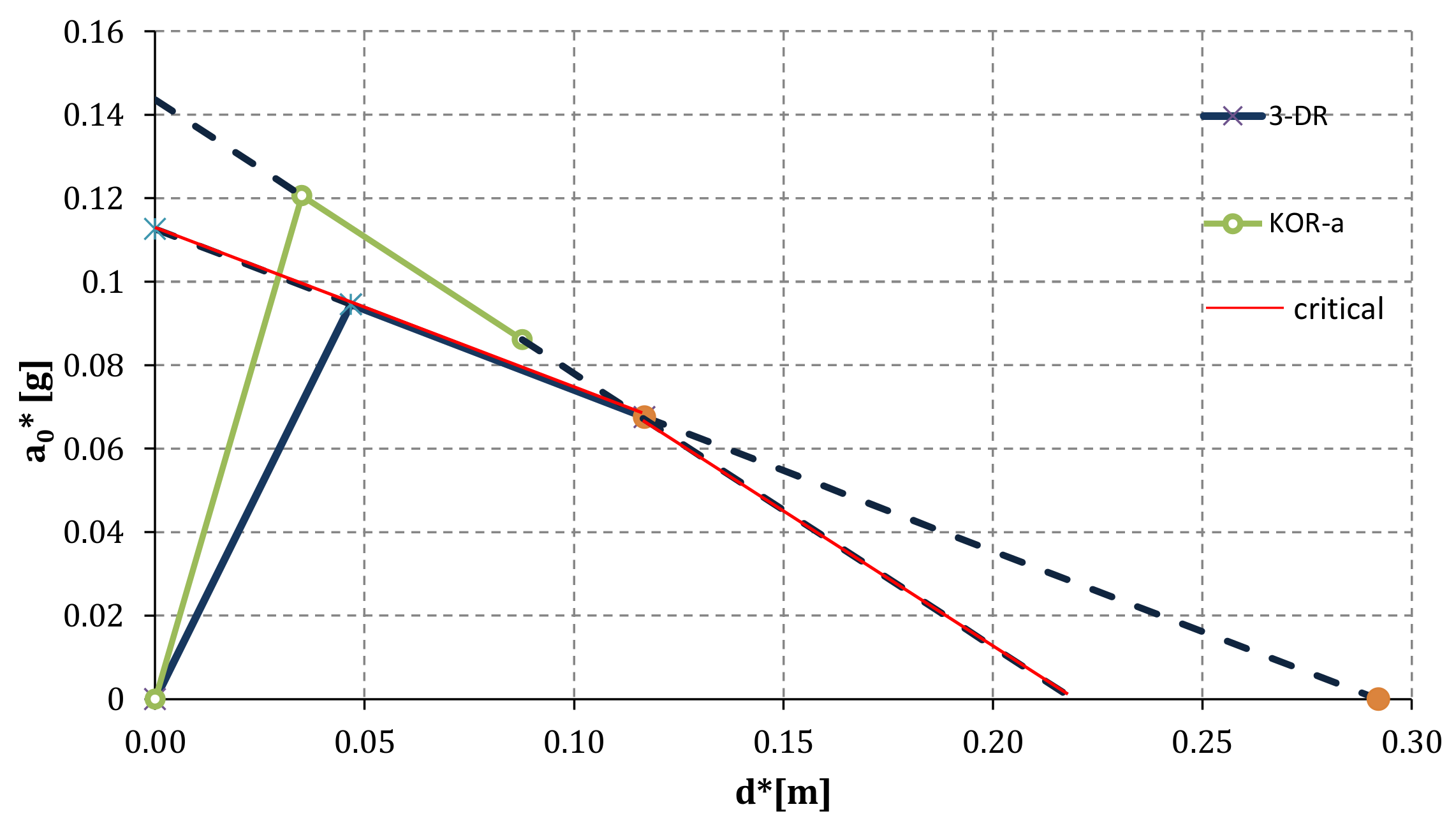
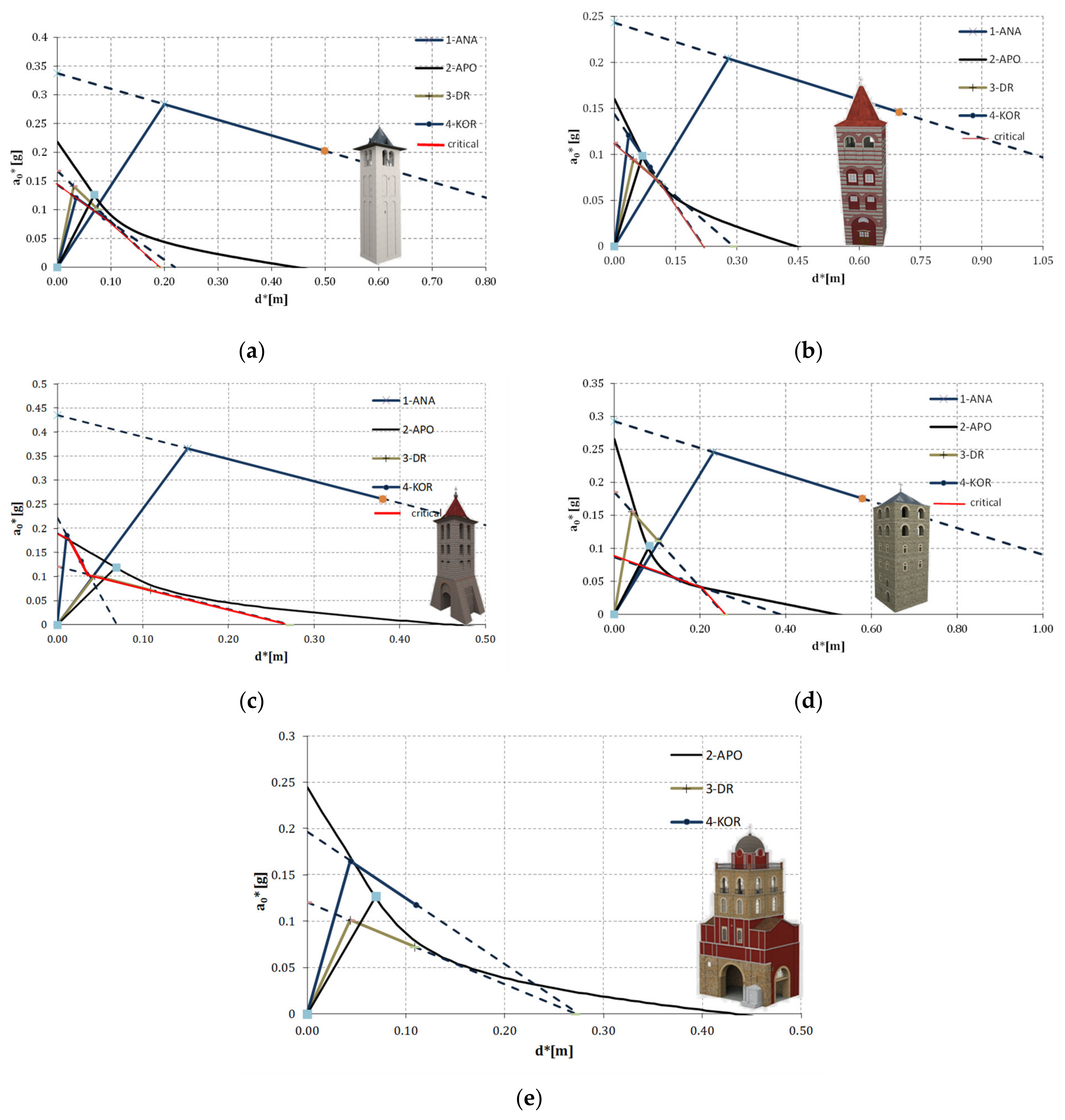
5. Filtering Effect
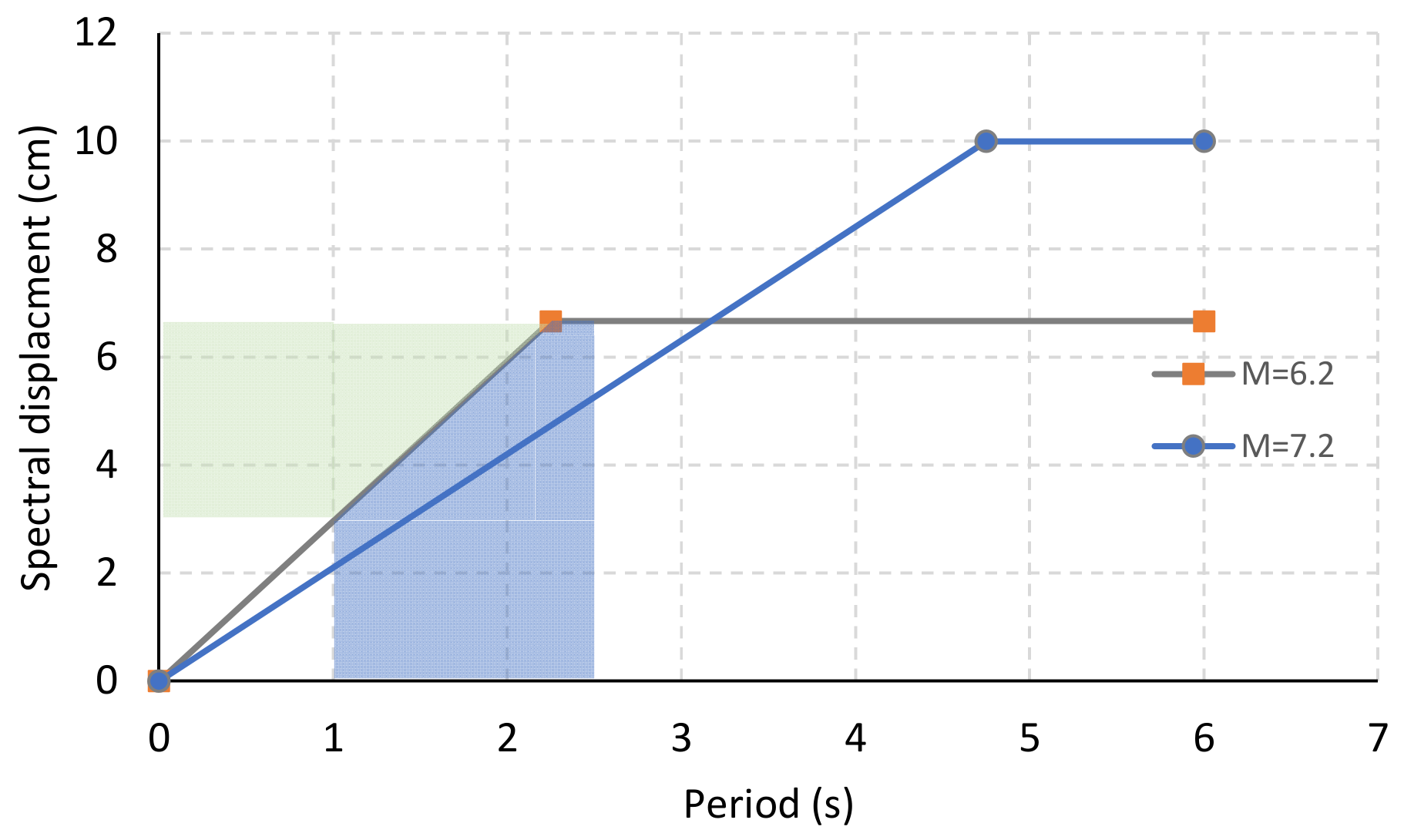
6. Seismic Response
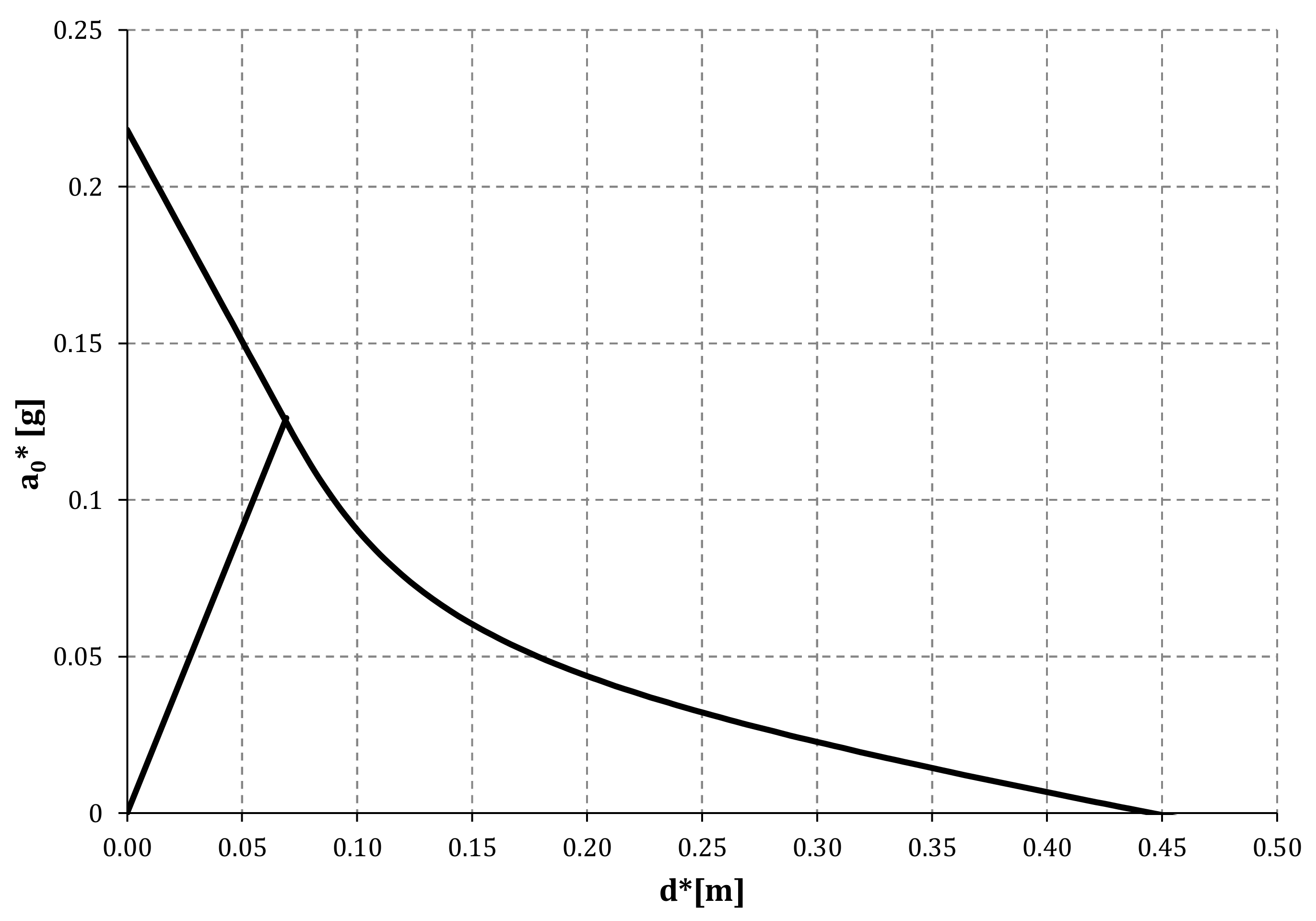
6.1. Capacity Curves
6.2. Vulnerability Curves
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferreira, T.M.; Costa, A.A.; Costa, A. Analysis of the Out-Of-Plane Seismic Behavior of Unreinforced Masonry: A Literature Review. Int. J. Arch. Herit. 2014, 9, 949–972. [Google Scholar] [CrossRef]
- Indirli, M.; Kouris, L.A.S.; Formisano, A.; Borg, R.P.; Mazzolani, F.M. Seismic Damage Assessment of Unreinforced Masonry Structures After the Abruzzo 2009 Earthquake: The Case Study of the Historical Centers of L’Aquila and Castelvecchio Subequo. Int. J. Arch. Herit. 2013, 7, 536–578. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Borg, R.P.; Indirli, M. The L’Aquila Earthquake, April 6th, 2009: A Review of Seismic Damage Mechanisms. In Proceedings of the COST ACTION C26: Urban Habitat Constructions Under Catastrophic Events—Proceedings of the Final Conference, Naples, Italy, 16–18 September 2010; Mazzolani, F.M., Ed.; Taylor & Francis Group: London, UK, 2010; pp. 673–681. [Google Scholar]
- Borg, R.P.R.; Indirli, M.; Rossetto, T.; Kouris, L.A. L’Aquila Earthquake April 6th, 2009: Damage Assessment Methodologies. In Proceedings of the Urban Habitat Constructions under Catastrophic Events, Naples, Italy, 16–18 September 2010; Mazzolani, F.M., Ed.; Taylor & Francis Group: London, UK, 2010; pp. 557–564. [Google Scholar]
- Kouris, L.A.S.; Kappos, A.J. Detailed and simplified non-linear models for timber-framed masonry structures. J. Cult. Herit. 2012, 13, 47–58. [Google Scholar] [CrossRef] [Green Version]
- Kouris, L.A.; Kappos, A.J. Seismic Performance of Ancient Timber-Framed Walls. In Proceedings of the 4th International Congress: Science and Technology for the Safeguard of Cultural Heritage of the Mediterranean Basin, Cairo, Egypt, 6–8 December 2009; Ferrari, A., Ed.; CNR, Inst. of Chemical Methodologies: Rome, Italy, 2009; Volume 3, pp. 119–127. [Google Scholar]
- Kouris, L.A.S.; Kappos, A.J. Numerical Investigation and Empirical Seismic Vulnerability Assessment of Timber-Framed Masonry Buildings. 2015. ISBN 9781466682870/1466682868/9781466682863. Available online: https://www.scienceopen.com/book?vid=03549d92-5059-4d17-a6a1-70290a881f96 (accessed on 14 March 2017).
- Kouris, E.; Kouris, L. Investigation of the Influence of Tie-Rods on the Seismic Behaviour of Slender Towers. Proc. Twelfth Int. Conf. Comput. Struct. Technol. 2014, 106. [Google Scholar] [CrossRef]
- Augusti, G.; Ciampoli, M.; Giovenale, P. Seismic vulnerability of monumental buildings. Struct. Saf. 2001, 23, 253–274. [Google Scholar] [CrossRef]
- Giordano, A.; De Luca, A.; Mele, E.; Romano, A. A simple formula for predicting the horizontal capacity of masonry portal frames. Eng. Struct. 2007, 29, 2109–2123. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Mele, E.; De Luca, A.; Giordano, A. Modelling and analysis of a basilica under earthquake loading. J. Cult. Herit. 2003, 4, 355–367. [Google Scholar] [CrossRef]
- Giresini, L.; Fragiacomo, M.; Sassu, M. Rocking analysis of masonry walls interacting with roofs. Eng. Struct. 2016, 116, 107–120. [Google Scholar] [CrossRef] [Green Version]
- Menon, A.; Magenes, G. Definition of Seismic Input for Out-of-Plane Response of Masonry Walls: I. Parametric Study. J. Earthq. Eng. 2011, 15, 195–213. [Google Scholar] [CrossRef]
- Lam, N.; Griffith, M.; Wilson, J.; Doherty, K. Time–history analysis of URM walls in out-of-plane flexure. Eng. Struct. 2003, 25, 743–754. [Google Scholar] [CrossRef]
- Preciado, A.; Sperbeck, S.T.; Ramírez-Gaytán, A. Seismic vulnerability enhancement of medieval and masonry bell towers externally prestressed with unbonded smart tendons. Eng. Struct. 2016, 122, 50–61. [Google Scholar] [CrossRef]
- Kouris, S.S.; Weber, M.K.K. Numerical Analysis of Masonry Bell-Towers under Dynamic Loading. J. Civ. Eng. Arch. 2011, 5, 715–722. [Google Scholar]
- Kouris, S.S.; Karaveziroglou-Weber, M. Research on the Seismic Strengthening of a Medieval Masonry Campanile. Struct. Eng. 2009, 87, 20–24. [Google Scholar]
- Casolo, S.; Milani, G.; Uva, G.; Alessandri, C. Comparative seismic vulnerability analysis on ten masonry towers in the coastal Po Valley in Italy. Eng. Struct. 2013, 49, 465–490. [Google Scholar] [CrossRef]
- Ubertini, F.; Cavalagli, N.; Kita, A.; Comanducci, G. Assessment of a monumental masonry bell-tower after 2016 Central Italy seismic sequence by long-term SHM. Bull. Earthq. Eng. 2018, 16, 775–801. [Google Scholar] [CrossRef]
- Kouris, S.S.; Karaveziroglou-Weber, M.K. Structural Analysis and Diagnosis of Masonry Towers. In Proceedings of the ECCOMAS Thematic Conference—COMPDYN 2011: 3rd International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering: An IACM Special Interest Conference, Corfu, Greece, 25–28 May 2011; Papadrakakis, M., Fragiadakis, M., Plevris, V., Eds.; National Technical University of Athens: Athens, Greece, 2011. [Google Scholar]
- Landi, L.; Gabellieri, R.; Diotallevi, P.P. A model for the out-of-plane dynamic analysis of unreinforced masonry walls in buildings with flexible diaphragms. Soil Dyn. Earthq. Eng. 2015, 79, 211–222. [Google Scholar] [CrossRef]
- Abrams, D.P. Response of Unreinforced Masonry Buildings. J. Earthq. Eng. 1997, 1, 257–273. [Google Scholar] [CrossRef]
- Portioli, F.; Casapulla, C.; Cascini, L.; D’Aniello, M.; Landolfo, R. Limit analysis by linear programming of 3D masonry structures with associative friction laws and torsion interaction effects. Arch. Appl. Mech. 2013, 83, 1415–1438. [Google Scholar] [CrossRef]
- Pasiou, E.D.; Kourkoulis, S.K. Mechanical response of marble epistyles under shear: Numerical analysis using an experimentally validated model. J. Mech. Behav. Mater. 2018, 27, 27. [Google Scholar] [CrossRef]
- Kouris, L.A.; Valsamos, G.; Triantafyllou, S.; Karlos, V.; Pohoryles, D.A.; Bournas, D.A.; Larcher, M.; Casadei, F. Protection of Masonry Structures against Explosions Applying Layers of Textile Reinforced Mortar. In Proceedings of the International Conference on Structural Dynamic, EURODYN, Athens, Greece, 13–25 November 2020; Papadrakakis, M., Fragiadakis, M., Papadimitriou, C., Eds.; National Technical University of Athens (NTUA): Athens, Greece, 2020; Volume 2, pp. 2573–2584. [Google Scholar]
- Kouris, L.A.S. Practical Simulation Tools for the Seismic Analysis of Timber-Framed Masonry Structures. In Historical Earthquake-Resistant Timber Frames in the Mediterranean Area; Ruggieri, N., Tampone, G., Zinno, R., Eds.; Springer: Cham, Switzerland, 2013. [Google Scholar]
- Kouris, L.A.S.; Meireles, H.; Bento, R.; Kappos, A.J. Simple and complex modelling of timber-framed masonry walls in Pombalino buildings. Bull. Earthq. Eng. 2014, 12, 1777–1803. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Kappos, A.J. A practice-oriented model for pushover analysis of a class of timber-framed masonry buildings. Eng. Struct. 2014, 75, 489–506. [Google Scholar] [CrossRef]
- Habieb, A.B.; Valente, M.; Milani, G. Effectiveness of different base isolation systems for seismic protection: Numerical insights into an existing masonry bell tower. Soil Dyn. Earthq. Eng. 2019, 125, 105752. [Google Scholar] [CrossRef]
- Shehu, R. Preliminary Assessment of the Seismic Vulnerability of Three Inclined Bell-towers in Ferrara, Italy. Int. J. Arch. Herit. 2020, 1–33. [Google Scholar] [CrossRef]
- Pintucchi, B.L.; Zani, N. Effectiveness of nonlinear static procedures for slender masonry towers. Bull. Earthq. Eng. 2014, 12, 2531–2556. [Google Scholar] [CrossRef]
- Gambarotta, L.; Lagomarsino, S. Damage Models for the Seismic Response of Brick Masonry Shear Walls. Part II: The Continuum Model and Its Applications. Earthq. Eng. Struct. Dyn. 1997, 26, 423–439. [Google Scholar] [CrossRef]
- Psycharis, I.N.; Lemos, J.V.; Papastamatiou, D.Y.; Zambas, C.; Papantonopoulos, C. Numerical study of the seismic behaviour of a part of the Parthenon Pronaos. Earthq. Eng. Struct. Dyn. 2003, 32, 2063–2084. [Google Scholar] [CrossRef]
- Lemos, J.V. Discrete Element Modeling of Masonry Structures. Int. J. Arch. Herit. 2007, 1, 190–213. [Google Scholar] [CrossRef]
- Ferrante, A.; Clementi, F.; Milani, G. Dynamic Behavior of an Inclined Existing Masonry Tower in Italy. Front. Built Environ. 2019, 5, 33. [Google Scholar] [CrossRef]
- Peña, F.; Prieto, F.; Lourenço, P.B.; Campos Costa, A.; Lemos, J.V. On the Dynamics of Rocking Motion of Single Rigid-Block Structures. Earthq. Eng. Struct. Dyn. 2007, 36, 2383–2399. [Google Scholar] [CrossRef] [Green Version]
- Lagomarsino, S. Seismic assessment of rocking masonry structures. Bull. Earthq. Eng. 2015, 13, 97–128. [Google Scholar] [CrossRef]
- Sorrentino, L.; Masiani, R.; Benedetti, S. Experimental Estimation of Energy Damping during Free Rocking of Unreinforced Masonry Walls. First Results. Aip Conf. Proc. 2008, 1020, 1888–1895. [Google Scholar] [CrossRef]
- Doherty, K.; Griffith, M.C.; Lam, N.; Wilson, J. Displacement-Based Seismic Analysis for out-of-Plane Bending of Unreinforced Masonry Walls. Earthq. Eng. Struct. Dyn. 2002, 31, 833–850. [Google Scholar] [CrossRef]
- Sarhosis, V.; Milani, G.; Formisano, A.; Fabbrocino, F. Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull. Earthq. Eng. 2018, 16, 1511–1545. [Google Scholar] [CrossRef] [Green Version]
- Mallardo, V.; Malvezzi, R.; Milani, E.; Milani, G. Seismic vulnerability of historical masonry buildings: A case study in Ferrara. Eng. Struct. 2008, 30, 2223–2241. [Google Scholar] [CrossRef]
- Kouris, E.-G. Dynamic Characteristics and Rocking Response of a Byzantine Medieval Tower. J. Civ. Eng. Sci. 2017, 6, 14–23. [Google Scholar] [CrossRef] [Green Version]
- Makris, N.; Alexakis, H. Limit equilibrium analysis of masonry buttresses and towers under lateral and gravity loads. Arch. Appl. Mech. 2015, 85, 1915–1940. [Google Scholar] [CrossRef]
- Saisi, A.; Gentile, C. Investigation Strategy for Structural Assessment of Historic Towers. Infrastructures 2020, 5, 106. [Google Scholar] [CrossRef]
- Chrysostomou, C.; Kyriakides, N.; Kappos, A.; Kouris, L.; Georgiou, E.; Millis, M. Seismic Retrofitting and Health Monitoring of School Buildings of Cyprus. Open Constr. Build. Technol. J. 2013, 7, 208–220. [Google Scholar] [CrossRef] [Green Version]
- Ubertini, F.; Comanducci, G.; Cavalagli, N. Vibration-based structural health monitoring of a historic bell-tower using output-only measurements and multivariate statistical analysis. Struct. Health Monit. 2016, 15, 438–457. [Google Scholar] [CrossRef]
- Chrysostomou, C.Z.; Kyriakides, N.; Kappos, A.J.; Kouris, L.; Papanikolaou, V.; Dimitrakopoulos, E.G.; Giouvanidis, A.I.; Georgiou, E. Seismic Safety and Vulnerability Mitigation of School Buildings. In Proceedings of the 4th International fib Congress 2014: Improving Performance of Concrete Structures, FIB 2014, Mumbai, India, 10–13 February 2014; pp. 122–124. [Google Scholar]
- Kouris, L.A.S.L.; Penna, A.; Magenes, G. Damage detection of an unreinforced stone masonry two storeys building based on damping estimate. In Brick and Block Masonry; CRC Press: Boca Raton, FL, USA, 2016; pp. 2425–2432. ISBN 978-1-138-02999-6. [Google Scholar]
- Kouris, L.A.S.; Penna, A.; Magenes, G. Seismic damage diagnosis of a masonry building using short-term damping measurements. J. Sound Vib. 2017, 394, 366–391. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Penna, A.; Magenes, G. Dynamic Modification and Damage Propagation of a Two-Storey Full-Scale Masonry Building. Adv. Civ. Eng. 2019, 2019, 1–21. [Google Scholar] [CrossRef]
- Gentile, C.; Saisi, A. Ambient vibration testing of historic masonry towers for structural identification and damage assessment. Constr. Build. Mater. 2007, 21, 1311–1321. [Google Scholar] [CrossRef]
- Stanko, D.; Markušić, S.; Strelec, S.; Gazdek, M. Seismic response and vulnerability of historical Trakošćan Castle, Croatia using HVSR method. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Standoli, G.; Giordano, E.; Milani, G.; Clementi, F. Model Updating of Historical Belfries Based on Oma Identification Techniques. Int. J. Arch. Herit. 2020, 1–25. [Google Scholar] [CrossRef]
- Bru, D.; Ivorra, S.; Betti, M.; Adam, J.M.; Bartoli, G. Parametric dynamic interaction assessment between bells and supporting slender masonry tower. Mech. Syst. Signal Process. 2019, 129, 235–249. [Google Scholar] [CrossRef]
- Stober, D.; Žarnić, R.; Penava, D.; Podmanicki, M.T.; Virgej-Đurašević, R. Application of HBIM as a Research Tool for Historical Building Assessment. Civ. Eng. J. 2018, 4, 1565. [Google Scholar] [CrossRef] [Green Version]
- KEDAK. The Towers of Mount Athos; Konstantinou, M., Nicodimos, L., Papangellos, I., Moustakas, S., Eds.; Ministry of Macedonia-Thrace, Centre for Preservation of Mount Athos Heritage: Thessaloniki, Greece, 2002; ISBN 960-859-67-7-7. [Google Scholar]
- Munteanu, P.B.; The Archaeology of the Medieval Towers in Mount Athos. An Attempt of Archaeological Research. Rev. Transilv. 2017, 6, 65–67. Available online: http://digital-library.ulbsibiu.ro/jspui/bitstream/123456789/1981/15/12%20-%20Muntean%20Besliu%20Petre%20-%20The%20archaeology%20of%20the%20medieval%20towers%20in%20Mount%20Athos.pdf (accessed on 15 April 2018).
- Torelli, G.; D’Ayala, D.; Betti, M.; Bartoli, G. Analytical and numerical seismic assessment of heritage masonry towers. Bull. Earthq. Eng. 2020, 18, 969–1008. [Google Scholar] [CrossRef] [Green Version]
- Milani, G. Fast Vulnerability Evaluation of Masonry Towers by Means of an Interactive and Adaptive 3D Kinematic Limit Analysis with Pre-assigned Failure Mechanisms. Int. J. Arch. Herit. 2019, 13, 941–962. [Google Scholar] [CrossRef]
- Liakos, D. The Byzantine bell-tower in Vatopedi Monastery on Mount Athos (1427). The Sculpted decoration and its significance (with 24 figures). Jahrb. Der Osterr. Byz. 2016, 1, 153–168. [Google Scholar] [CrossRef]
- Kouris, E.G. Recent Methodologies for Estimating Traditional Structures. Ph.D. Thesis, Aristotle Univeristy of Thessaloniki, Thessaloniki, Greece, 2019. [Google Scholar]
- Penava, D.; Kraus, I.; Petronijević, M.; Schmid, G. Dynamic Soil-Structure Analysis of Tower-Like Structures Using Spectral Elements. Teh. Vjesn. Tech. Gaz. 2018, 25, 738–747. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Calderini, C. The dynamical identification of the tensile force in ancient tie-rods. Eng. Struct. 2005, 27, 846–856. [Google Scholar] [CrossRef]
- Milani, G.; Lourenço, P.; Tralli, A. 3D homogenized limit analysis of masonry buildings under horizontal loads. Eng. Struct. 2007, 29, 3134–3148. [Google Scholar] [CrossRef] [Green Version]
- Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J.C.A. Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef] [Green Version]
- Kappos, A.J.; Penelis, G.G.; Drakopoulos, C.G. Evaluation of Simplified Models for Lateral Load Analysis of Unreinforced Masonry Buildings. J. Struct. Eng. 2002, 128, 890–897. [Google Scholar] [CrossRef]
- Quinn, N.; D’Ayala, D. Assessment of the Realistic Stiffness and Capacity of the Connections in Quincha Frames to Develop Numerical Models. In Proceedings of the 2nd International Conference on Structural Health Assessment of Timber Structures, SHATIS 2013, Trento, Italy, 4–6 September 2013; Volume 778, pp. 526–533. [Google Scholar]
- Kouris, L.A.S.; Bournas, D.A.; Akintayo, O.T.; Konstantinidis, A.A.; Aifantis, E.C. A gradient elastic homogenisation model for brick masonry. Eng. Struct. 2020, 208, 110311. [Google Scholar] [CrossRef]
- Hendry, A.W. Structural Masonry; Macmillan Press: London, UK, 1998. [Google Scholar]
- Bartoli, G.; Betti, M.; Giordano, S. In situ static and dynamic investigations on the “Torre Grossa” masonry tower. Eng. Struct. 2013, 52, 718–733. [Google Scholar] [CrossRef]
- Boschi, S.; Galano, L.; Vignoli, A. Mechanical characterisation of Tuscany masonry typologies by in situ tests. Bull. Earthq. Eng. 2019, 17, 413–438. [Google Scholar] [CrossRef]
- Moropoulou, A.; Cakmak, A.; Lohvyn, N. Earthquake resistant construction techniques and materials on Byzantine monuments in Kiev. Soil Dyn. Earthq. Eng. 2000, 19, 603–615. [Google Scholar] [CrossRef]
- Çakmak, A.; Moropoulou, A.; Mullen, C. Interdisciplinary study of dynamic behavior and earthquake response of Hagia Sophia. Soil Dyn. Earthq. Eng. 1995, 14, 125–133. [Google Scholar] [CrossRef]
- CEN. Eurocode 5: Design of Timber Structures. EN 1995; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Saisi, A.; Gentile, C.; Guidobaldi, M. Post-earthquake continuous dynamic monitoring of the Gabbia Tower in Mantua, Italy. Constr. Build. Mater. 2015, 81, 101–112. [Google Scholar] [CrossRef]
- Saisi, A.; Guidobaldi, M.; Gentile, C. On Site Investigation and Continuous Dynamic Monitoring of a Historic Tower in Mantua, Italy. In Proceedings of the 6th International Conference on Emerging Technologies in Nondestructive Testing(ETNDT6), Brussels, Belgium, 27–29 May 2015. [Google Scholar]
- Bayraktar, A.; Türker, T.; Sevım, B.; Altunişik, A.C.; Yildirim, F. Modal Parameter Identification of Hagia Sophia Bell-Tower via Ambient Vibration Test. J. Nondestruct. Eval. 2009, 28, 37–47. [Google Scholar] [CrossRef]
- Russo, G.; Bergamo, O.; Damiani, L.; Lugato, D. Experimental analysis of the “Saint Andrea” Masonry Bell Tower in Venice. A new method for the determination of “Tower Global Young’s Modulus E.”. Eng. Struct. 2010, 32, 353–360. [Google Scholar] [CrossRef]
- Ivorra, S.; Palomo, M.J.; Verdu, G.; Zasso, A. Dynamic Forces Produced by Swinging Bells. Meccanica 2006, 41, 47–62. [Google Scholar] [CrossRef]
- DiTommaso, R.; Mucciarelli, M.; Parolai, S.; Picozzi, M. Monitoring the structural dynamic response of a masonry tower: Comparing classical and time-frequency analyses. Bull. Earthq. Eng. 2012, 10, 1221–1235. [Google Scholar] [CrossRef] [Green Version]
- Diaferio, M.; Foti, D.; Giannoccaro, N.I. Modal Parameters Identification on Environmental Tests of an Ancient Tower and Validation of Its FE Model. Int. J. Mech. 2016, 10, 80–89. [Google Scholar]
- Aloisio, A.; Capanna, I.; Cirella, R.; Alaggio, R.; Di Fabio, F.; Fragiacomo, M. Identification and Model Update of the Dynamic Properties of the San Silvestro Belfry in L’Aquila and Estimation of Bell’s Dynamic Actions. Appl. Sci. 2020, 10, 4289. [Google Scholar] [CrossRef]
- Bartoli, G.; Betti, M.; Vignoli, A. A numerical study on seismic risk assessment of historic masonry towers: A case study in San Gimignano. Bull. Earthq. Eng. 2016, 14, 1475–1518. [Google Scholar] [CrossRef]
- Preciado, A.; Budelmann, H.; Bartoli, G. Earthquake Protection of Colonial Bell Towers in Colima, Mexico with Externally Prestressed FRPs. Int. J. Arch. Herit. 2016, 10, 499–515. [Google Scholar] [CrossRef]
- Bassoli, E.; Vincenzi, L.; Bovo, M.; Mazzotti, C. Dynamic Identification of an Ancient Masonry Bell Tower Using a MEMS-Based Acquisition System. In Proceedings of the 2015 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS) Proceedings, IEEE. Trento, Italy, 9–10 July 2015; pp. 226–231. [Google Scholar]
- Ceroni, F.; Pecce, M.; Manfredi, G. Seismic Assessment of the Bell Tower of Santa Maria Del Carmine: Problems and Solutions. J. Earthq. Eng. 2009, 14, 30–56. [Google Scholar] [CrossRef] [Green Version]
- Gentile, C.; Saisi, A.; Cabboi, A. Structural Identification of a Masonry Tower Based on Operational Modal Analysis. Int. J. Arch. Herit. 2014, 9, 98–110. [Google Scholar] [CrossRef]
- Saisi, A.; Gentile, C.; Ruccolo, A. Pre-diagnostic prompt investigation and static monitoring of a historic bell-tower. Constr. Build. Mater. 2016, 122, 833–844. [Google Scholar] [CrossRef] [Green Version]
- Saisi, A.; Guidobaldi, M.; Gentile, C. On Site Investigation and Health Monitoring of a Historic Tower in Mantua, Italy. Appl. Sci. 2016, 6, 173. [Google Scholar] [CrossRef] [Green Version]
- Pieraccini, M.; Dei, D.; Mecatti, D.; Parrini, F. Dynamic Testing of Historic Towers Using an Interferometric Radar from an Unstable Measurement Position. J. Nondestruct. Eval. 2013, 32, 398–404. [Google Scholar] [CrossRef]
- Bartoli, G.; Betti, M.; Marra, A.M.; Monchetti, S. Semiempirical Formulations for Estimating the Main Frequency of Slender Masonry Towers. J. Perform. Constr. Facil. 2017, 31, 04017025. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Podestà, S.; Resemini, S. Seismic Response of Historical Churches. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002; p. 123. [Google Scholar]
- Kárník, V.; Procházková, D.; Schenková, Z.; Ruprechtová, L.; Dudek, A.; Drimmel, J.; Schmedes, E.; Leydecker, G.; Rothe, J.P.; Guterch, B.; et al. Map of isoseismals of the main Friuli earthquake of 6 May 1976. Pure Appl. Geophys. Pageoph 1978, 116, 1307–1313. [Google Scholar] [CrossRef] [Green Version]
- Bindi, D.; Pacor, F.; Luzi, L.; Massa, M.; Ameri, G. The Mw 6.3, 2009 L’Aquila Earthquake: Source, Path and Site Effects from Spectral Analysis of Strong Motion Data. Geophys. J. Int. 2009, 179, 1573–1579. [Google Scholar] [CrossRef] [Green Version]
- Decanini, L.; De Sortis, A.; Goretti, A.; Langenbach, R.; Mollaioli, F.; Rasulo, A. Performance of Masonry Buildings during the 2002 Molise, Italy, Earthquake. Earthq. Spectra 2004, 20, 191–220. [Google Scholar] [CrossRef]
- Abrams, D.P.; Angel, R.; Uzarski, J. Out-of-Plane Strength of Unreinforced Masonry Infill Panels. Earthq. Spectra 1996, 12, 825–844. [Google Scholar] [CrossRef]
- Ewing, R.D.; Kariotis, J.C. Methodology for Mitigation of Seismic Hazards in Existing Unreinforced Masonry Buildings: Wall Testing, Out-of-Plane. Topical Report 04. 1981. Available online: https://nehrpsearch.nist.gov/static/files/NSF/PB83125005.pdf (accessed on 15 March 2018).
- Lagomarsino, S. On the vulnerability assessment of monumental buildings. Bull. Earthq. Eng. 2006, 4, 445–463. [Google Scholar] [CrossRef]
- Griffith, M.C.; Magenes, G.; Melis, G.; Picchi, L. Evaluation of Out-of-Plane Stability of Unreinforced Masonry Walls Subjected to Seismic Excitation. J. Earthq. Eng. 2003, 7, 141–169. [Google Scholar] [CrossRef]
- Fajfar, P. Capacity Spectrum Method Based on Inelastic Demand Spectra. Earthq. Eng. Struct. Dyn. 1999, 28, 979–994. [Google Scholar] [CrossRef]
- Fajfar, P. A Nonlinear Analysis Method for Performance-Based Seismic Design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 6: Design of Masonry Structures; Part 1: General Rules for Buildings; CEN: Brussels, Belgium, 2004; Volume 1. [Google Scholar]
- Fonti, R.; Borri, A.; Barthel, R.; Candela, M.; Formisano, A. Rubble Masonry Response under Cyclic Actions: Experimental Tests and Theoretical Models. Int. J. Mason. Res. Innov. 2017, 2. [Google Scholar] [CrossRef]
- Formisano, A. Seismic Behaviour and Retrofitting of the Poggio Picenze Historical Centre Damaged by the L’Aquila Earthquake. In Proceedings of the 11th International Conference on Computational Structures Technology, Dubrovnik, Croatia, 4–7 September 2012; Topping, B.H.V., Ed.; Civil-Comp Press: Stirlingshire, UK, 2012; p. 199. [Google Scholar]
- Curti, E.; Podestà, S.; Scandolo, L. Simplified Mechanical Model for the Seismic Vulnerability Evaluation of Belfries. Int. J. Arch. Herit. 2012, 6, 605–625. [Google Scholar] [CrossRef]
- Vukobratović, V.; Fajfar, P. A method for the direct determination of approximate floor response spectra for SDOF inelastic structures. Bull. Earthq. Eng. 2015, 13, 1405–1424. [Google Scholar] [CrossRef]
- Politopoulos, I.; Feau, C. Some aspects of floor spectra of 1DOF nonlinear primary structures. Earthq. Eng. Struct. Dyn. 2007, 36, 975–993. [Google Scholar] [CrossRef] [Green Version]
- European Committee for Standardization. Eurocode 8, Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings. Eur. Stand. NF EN; CEN: Brussels, Belgium, 1998; Volume 1. [Google Scholar]
- Bommer, J.J.; Elnashai, A.S. Displacement Spectra for Seismic Design. J. Earthq. Eng. 1999, 3, 1–32. [Google Scholar] [CrossRef]
- Faccioli, E.; Paolucci, R.; Rey, J. Displacement Spectra for Long Periods. Earthq. Spectra 2004, 20, 347–376. [Google Scholar] [CrossRef]
- Tsapanos, T.M. Seismicity and Seismic Hazard Assessment in Greece; Springer: Dordrecht, The Netherlands, 2008; pp. 253–270. [Google Scholar]
- Kassaras, I.; Kapetanidis, V.; Ganas, A.; Tzanis, A.; Kosma, C.; Karakonstantis, A.; Valkaniotis, S.; Chailas, S.; Kouskouna, V.; Papadimitriou, P. The New Seismotectonic Atlas of Greece (v1.0) and Its Implementation. Geosciences 2020, 10, 447. [Google Scholar] [CrossRef]
- Whitman, R.V.; Anagnos, T.; Kircher, C.A.; Lagorio, H.J.; Lawson, R.S.; Schneider, P. Development of a National Earthquake Loss Estimation Methodology. Earthq. Spectra 1997, 13, 643–661. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Kappos, A.J. Fragility Curves and Loss Estimation for Traditional Timber-Framed Masonry Buildings in Lefkas, Greece. In Seismic Assessment, Behavior and Retrofit of Heritage Buildings and Monuments; Springer: Dordrecht, The Netherlands, 2015; Volume 37, pp. 199–233. [Google Scholar]
- Formisano, A.; Marzo, A. Simplified and refined methods for seismic vulnerability assessment and retrofitting of an Italian cultural heritage masonry building. Comput. Struct. 2017, 180, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Kouris, L.A.S.; Kappos, A.J. Derivation of Fragility Curves for Traditional Timber-Framed Masonry Buildings Using Nonlinear Static Analysis. In Proceedings of the 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Kos Island, Greece, 12–14 June 2013; pp. 1339–1348. [Google Scholar]
- Kouris, L.A.S. Seismic fragility curves for timber-framed masonry structures based on empirical damage data. Int. J. Sustain. Mater. Struct. Syst. 2016, 2, 233. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. HAZUS: Multi-Hazard Loss Estimation Methodology Technical and User’s Manual; FEMA: Washington, DC, USA, 2003.







| Monasteries | Total Height [m] | Base Height [m] | Belfry Altitude [m] | Main Structure Altitude [m] | Foundation Thickness [m] | Wall Thickness [m] | Area [m2] | |
|---|---|---|---|---|---|---|---|---|
 | Vatopedi | 25.55 | 7.20 | 19.00 | 14.40 | 1.80 | 0.85 | 20.25 |
| Philotheou | 24.90 | 6.00 | 18.90 | 16.50 | 1.15 | 1.05 | 30.25 | |
| Protaton | 24.00 | 7.20 | 19.00 | 14.40 | 1.08 | 0.85 | 20.25 | |
| Xenophontos | 19.50 | 2.00 | 17.00 | 11.60 | 1.20 | 1.05 | 49.00 | |
| Iveron | 20.52 | 5.00 | 19.00 | 17.00 | 1.05 | 1.05 | 45.00 |
| Elastic Modulus [GPa] | Poisson Ratio | Specific Weight [kN/m3] | |
|---|---|---|---|
| Masonry | 2.5 | 0.15 | 23 |
| Timber | 11 | 0.25 | 3.5 |
| Tower | Modal Periods (s) | Modal Frequencies (Hz) | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | |
| Vatopedi | 0.65 | 0.38 | 0.08 | 1.54 | 2.60 | 11.89 |
| Xenophontos | 0.29 | 0.14 | 0.08 | 3.48 | 7.26 | 12.79 |
| Iveron | 0.55 | 0.12 | 0.09 | 1.83 | 8.04 | 11.26 |
| Protaton | 0.34 | 0.19 | 0.07 | 2.92 | 5.18 | 14.60 |
| Philotheou | 0.44 | 0.29 | 0.08 | 2.28 | 3.47 | 12.24 |
| Empirical Equation | Vatopedi | Xenophontos | Iveron | Protaton | Philotheou |
|---|---|---|---|---|---|
| 1 | 1.39 | 3.51 | 2.27 | 1.78 | 2.52 |
| 2 | 1.72 | 2.04 | 1.81 | 2.53 | 2.45 |
| Designation | Collapse Mechanism | Out-of-Plane Damage |
|---|---|---|
| 1 - AΝA | Overturning |  |
| 2 - APO | Separation of perpendicular wall | 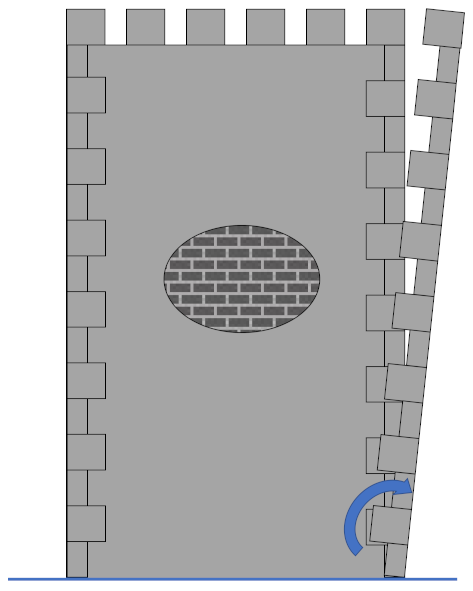 |
| 3 - DΡ | Diagonal cracking |  |
| 4 - ΚOΡ | Dislocation of the belfry | 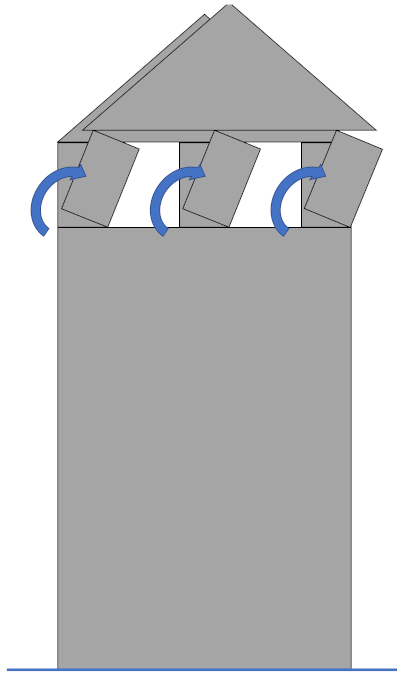 |
| Tower | Eff. Period (s) | Displacement Capacity (cm) | ||||
|---|---|---|---|---|---|---|
| 1 - AΝA | 2 - APO | 3 - DR | 4 - ΚOR | Spectral Displacement 1 | ||
| Vatopedi | 0.84 | 50 | 17 | 11 | 29 | 8 |
| Philotheou | 2.41 | 73 | 17 | 11 | 41 | 11 |
| Protaton | 2.25 | 38 | 17 | 11 | 41 | 13 |
| Xenophontos | 1.49 | 58 | 21 | 20 | 20 | 10 |
| Iveron | 2.20 | - | 18 | 14 | 41 | 12 |
| i | Mean | βT,ds,i | βds,i |
|---|---|---|---|
| 1 | 0.01 | 0.01 | 0.70 |
| 2 | 0.02 | 0.02 | 0.70 |
| 3 | 0.06 | 0.03 | 0.70 |
| 4 | 0.11 | 0.05 | 0.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kouris, E.-G.; Kouris, L.-A.S.; Konstantinidis, A.A.; Karayannis, C.G.; Aifantis, E.C. Assessment and Fragility of Byzantine Unreinforced Masonry Towers. Infrastructures 2021, 6, 40. https://doi.org/10.3390/infrastructures6030040
Kouris E-G, Kouris L-AS, Konstantinidis AA, Karayannis CG, Aifantis EC. Assessment and Fragility of Byzantine Unreinforced Masonry Towers. Infrastructures. 2021; 6(3):40. https://doi.org/10.3390/infrastructures6030040
Chicago/Turabian StyleKouris, Emmanouil-Georgios, Leonidas-Alexandros S. Kouris, Avraam A. Konstantinidis, Chris G. Karayannis, and Elias C. Aifantis. 2021. "Assessment and Fragility of Byzantine Unreinforced Masonry Towers" Infrastructures 6, no. 3: 40. https://doi.org/10.3390/infrastructures6030040
APA StyleKouris, E. -G., Kouris, L. -A. S., Konstantinidis, A. A., Karayannis, C. G., & Aifantis, E. C. (2021). Assessment and Fragility of Byzantine Unreinforced Masonry Towers. Infrastructures, 6(3), 40. https://doi.org/10.3390/infrastructures6030040