A Hidden Markov Model and Fuzzy Logic Forecasting Approach for Solar Geyser Water Heating
Abstract
:1. Introduction
2. Background
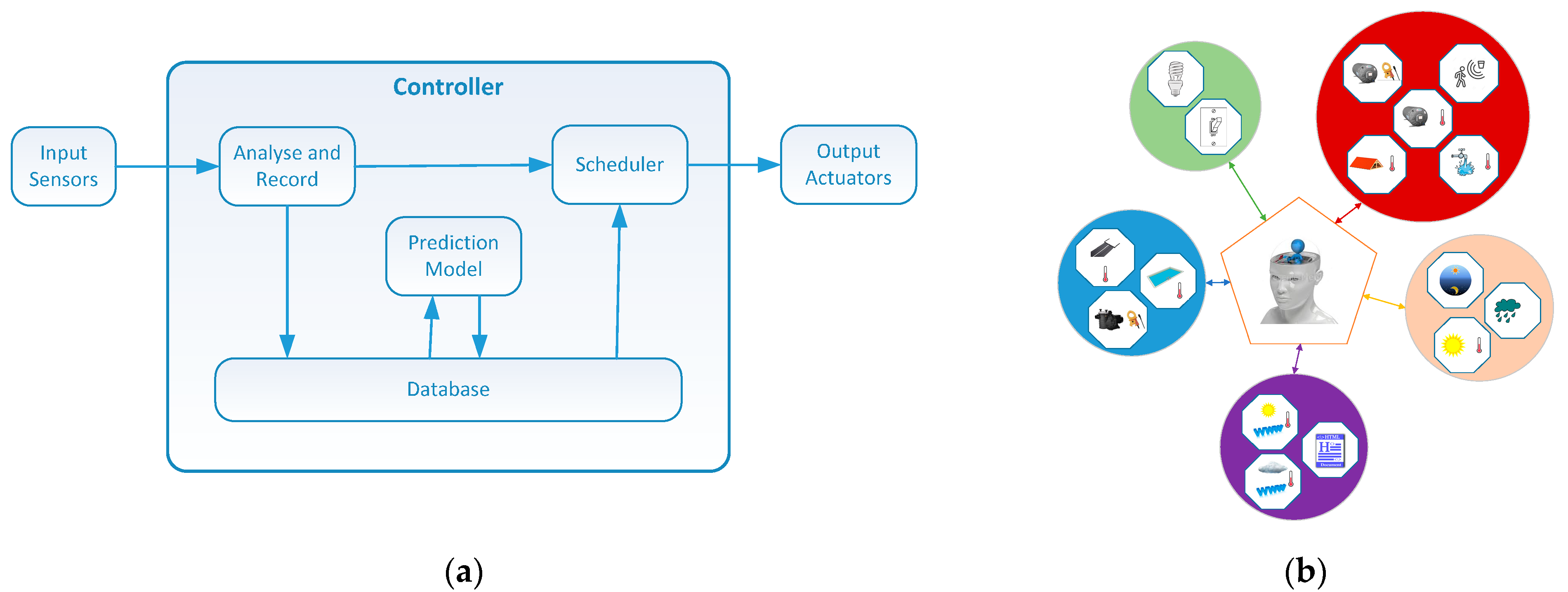
3. Methodology
3.1. Hardware Setup
3.2. Sensor Registration
3.3. Process Overview
| Algorithm 1: Fuzzified geyser, roof and pipe temperatures |
 |
| Algorithm 2: Baum–Welch algorithm modification 1 |
 |
| Algorithm 3: Baum–Welch algorithm |
 |
 |
| Algorithm 4: Calculate to enable geyser element |
 |
| Algorithm 5: Final prediction to enable geyser element |
 |
4. Data Analysis
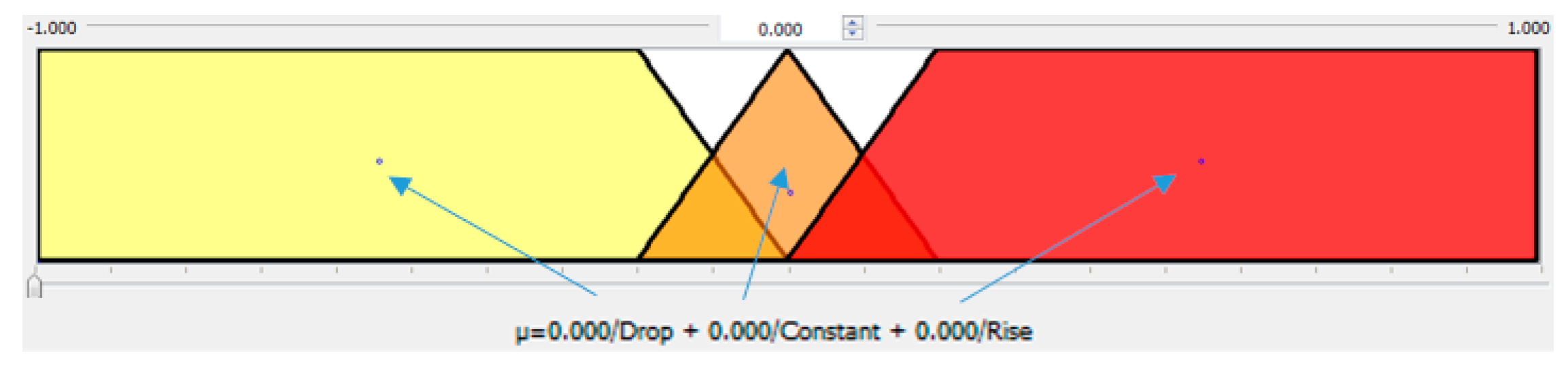
4.1. Fuzzified Geyser Usages
- DeltaGeyserTemp Set: DropHigh, DropMedium, DropLow and Heatup Membership;
- DeltaPipeTemp Set: CoolDown, Normal, SmallRise and LargeRise Membership;
- DeltaRoofTemp Set: Drop, Constant and Rise Membership function.
c)/droplow + (mx + c)/normal + (mx + c)/heatup
(mx + c)/largerise
µDeltaPipeTempCooldown(1) = 0.25
µDeltaPipeTempCooldown(1) = 0
4.2. Profile Solar Geyser Heating
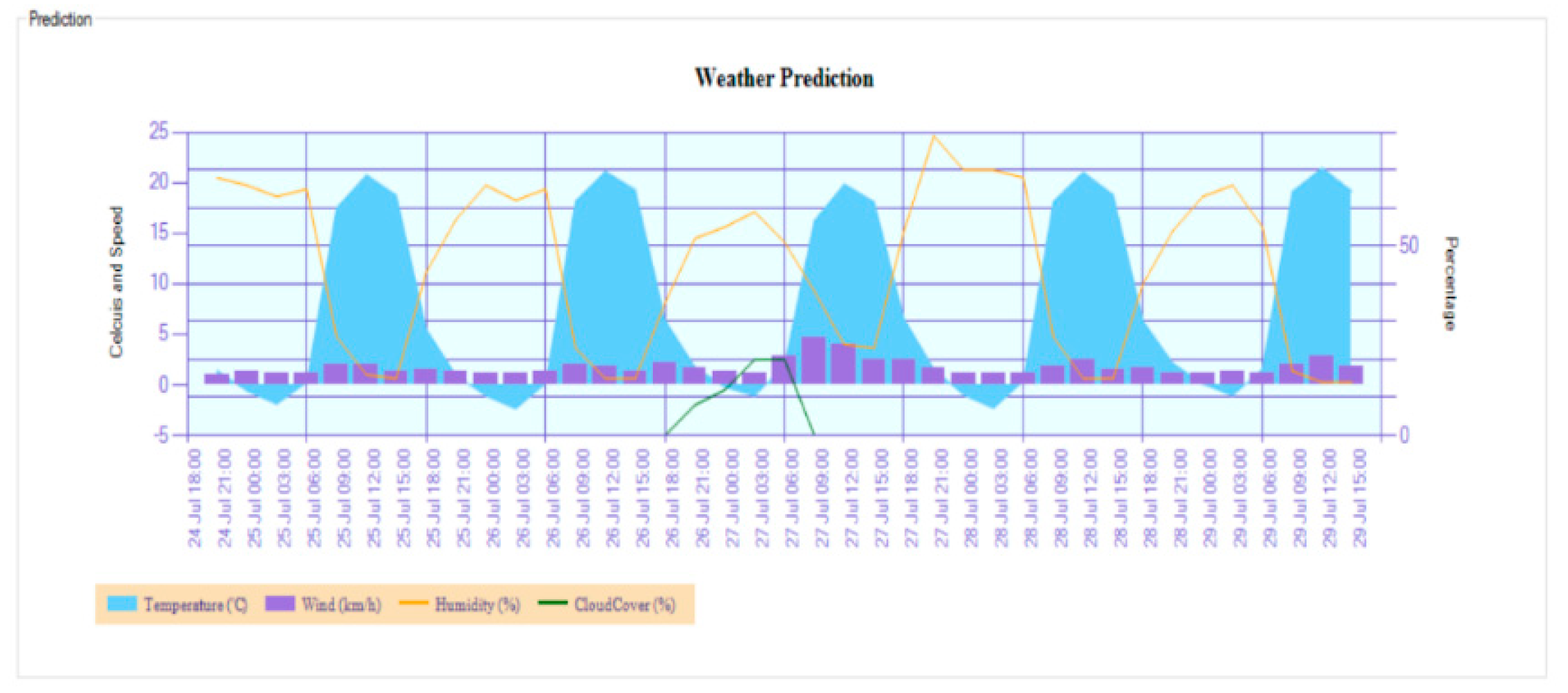
- Rainy season: High (January, February, March, April) where cloud cover and humidity goes above 70%;
- Rainy season: Low (October, November, December) where only cloud cover goes above 70%;
- Rainy season: None (May, June, July, August, September) where cloud cover and humidity readings are below 70% on average.
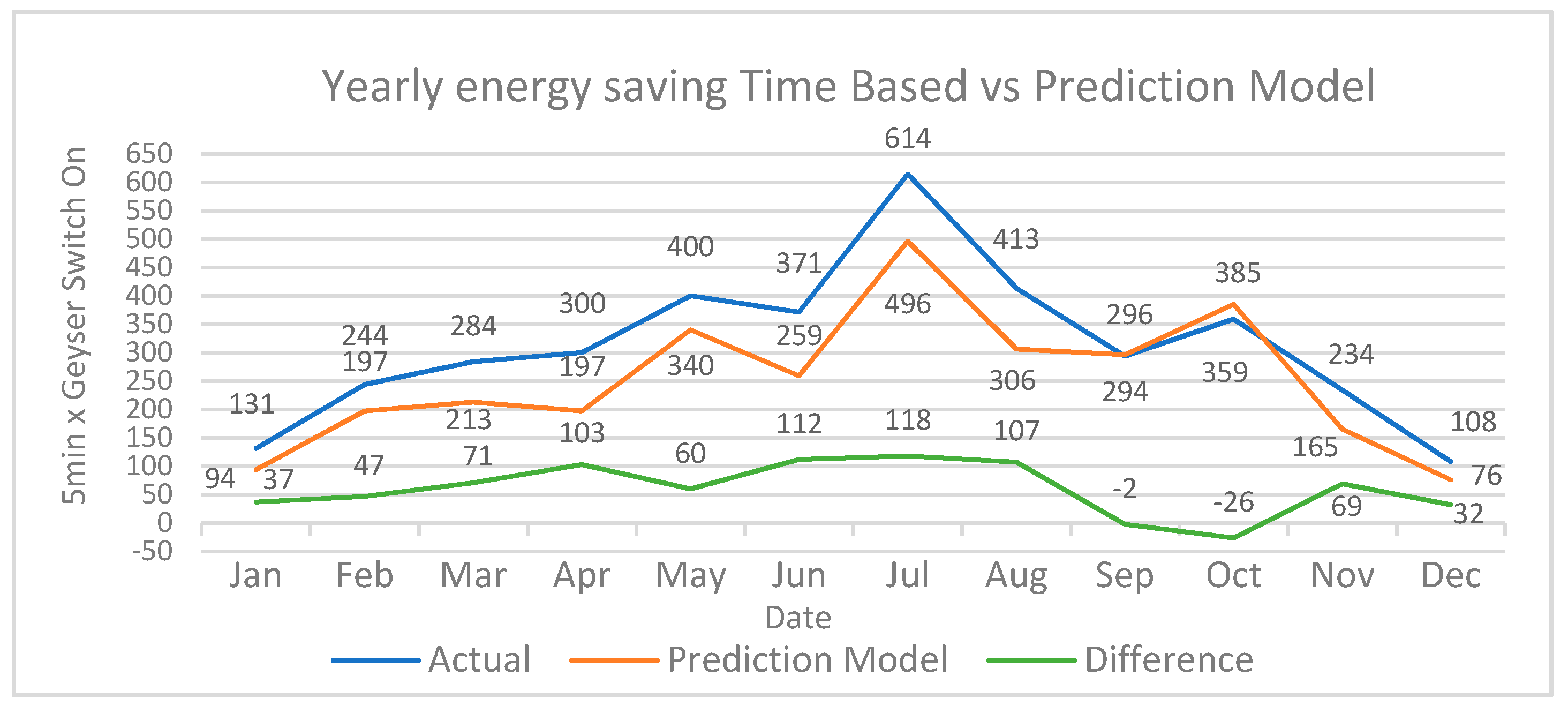
5. Results and Discussion
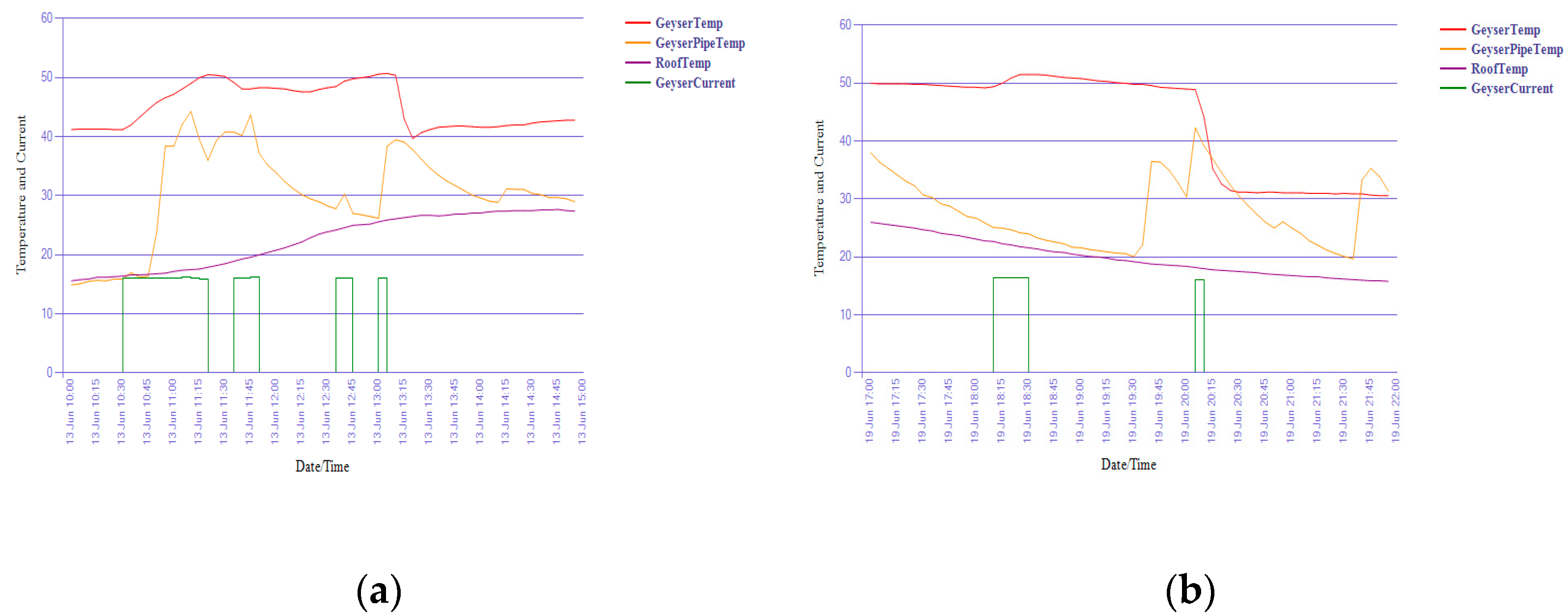
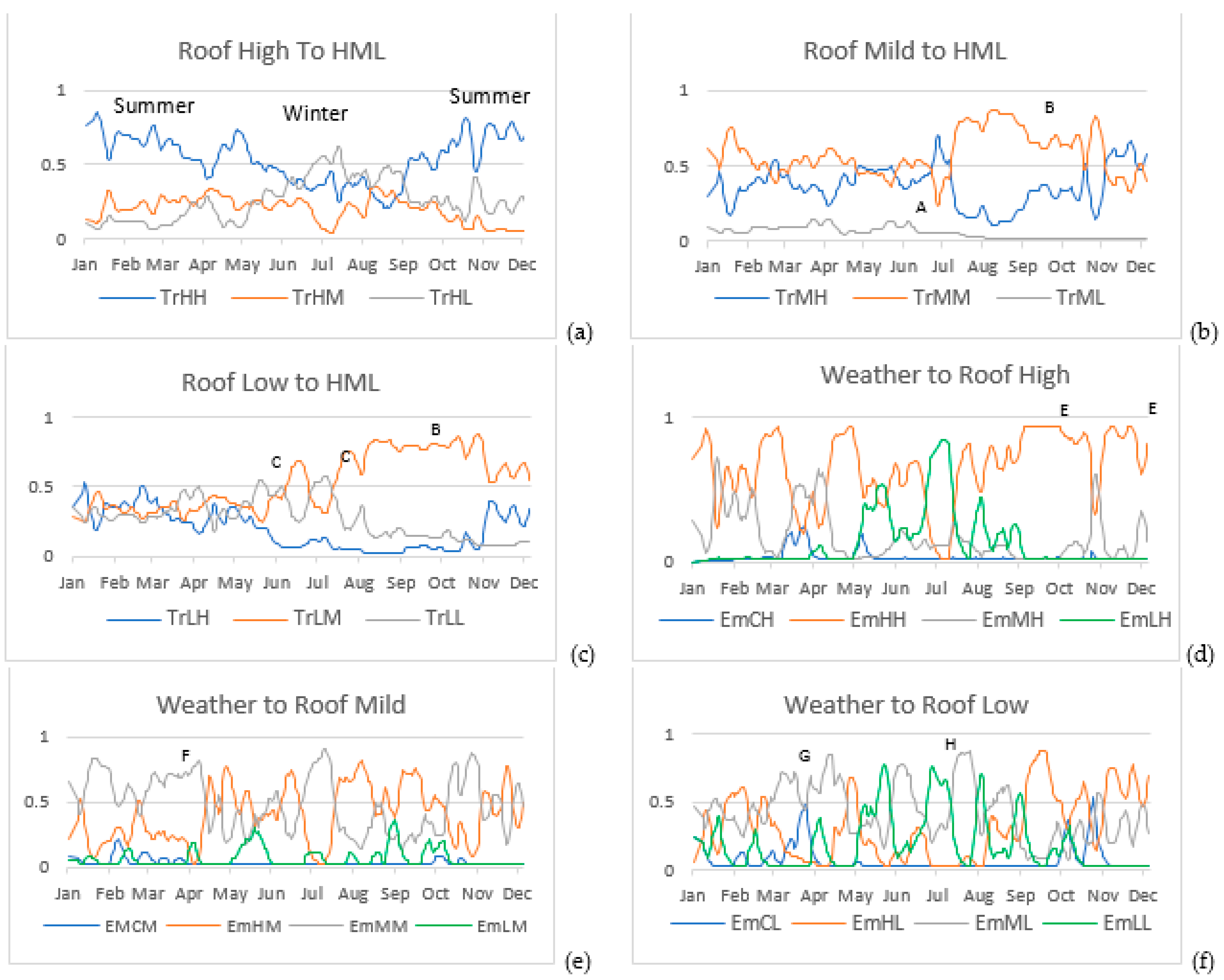
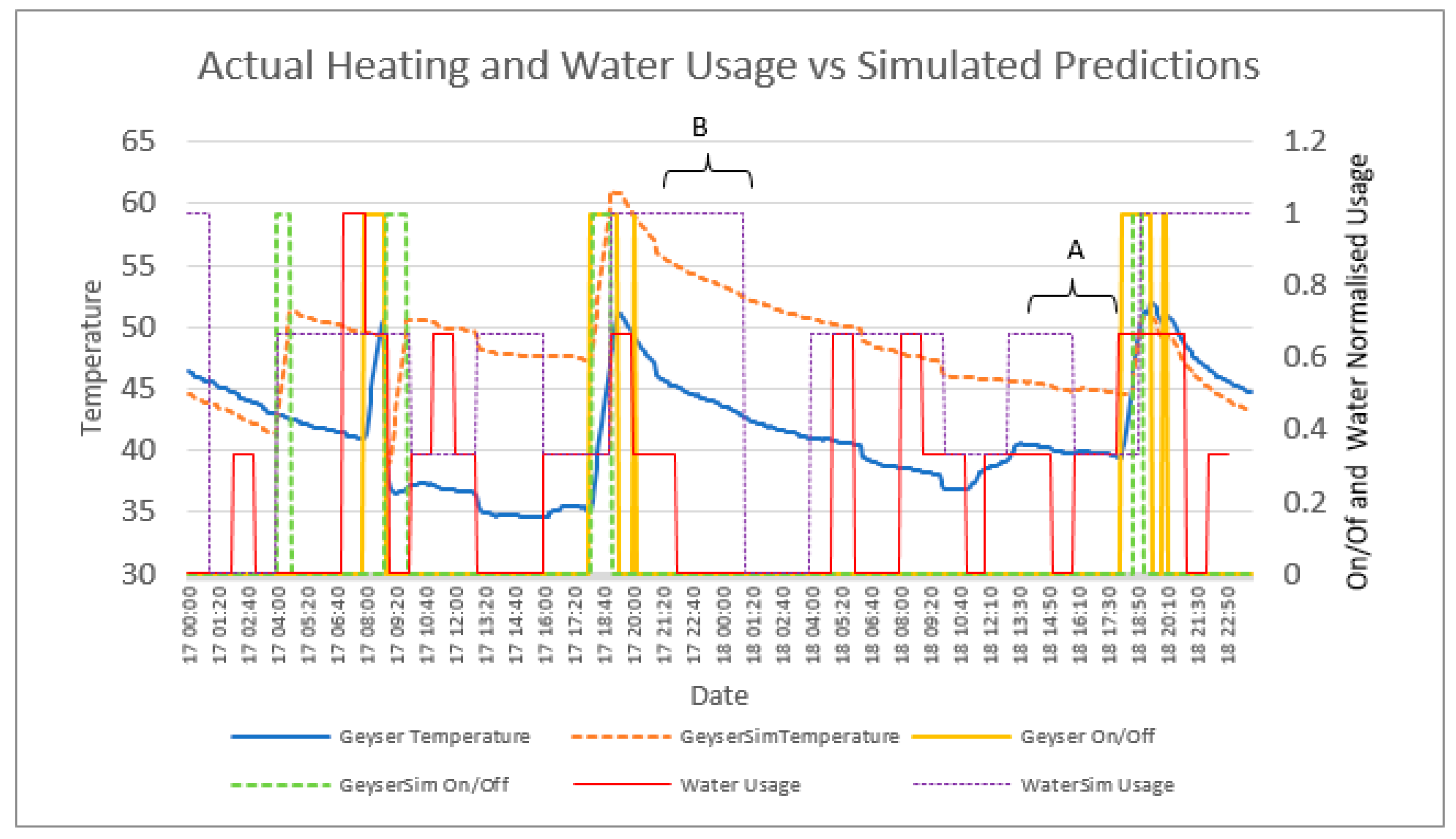
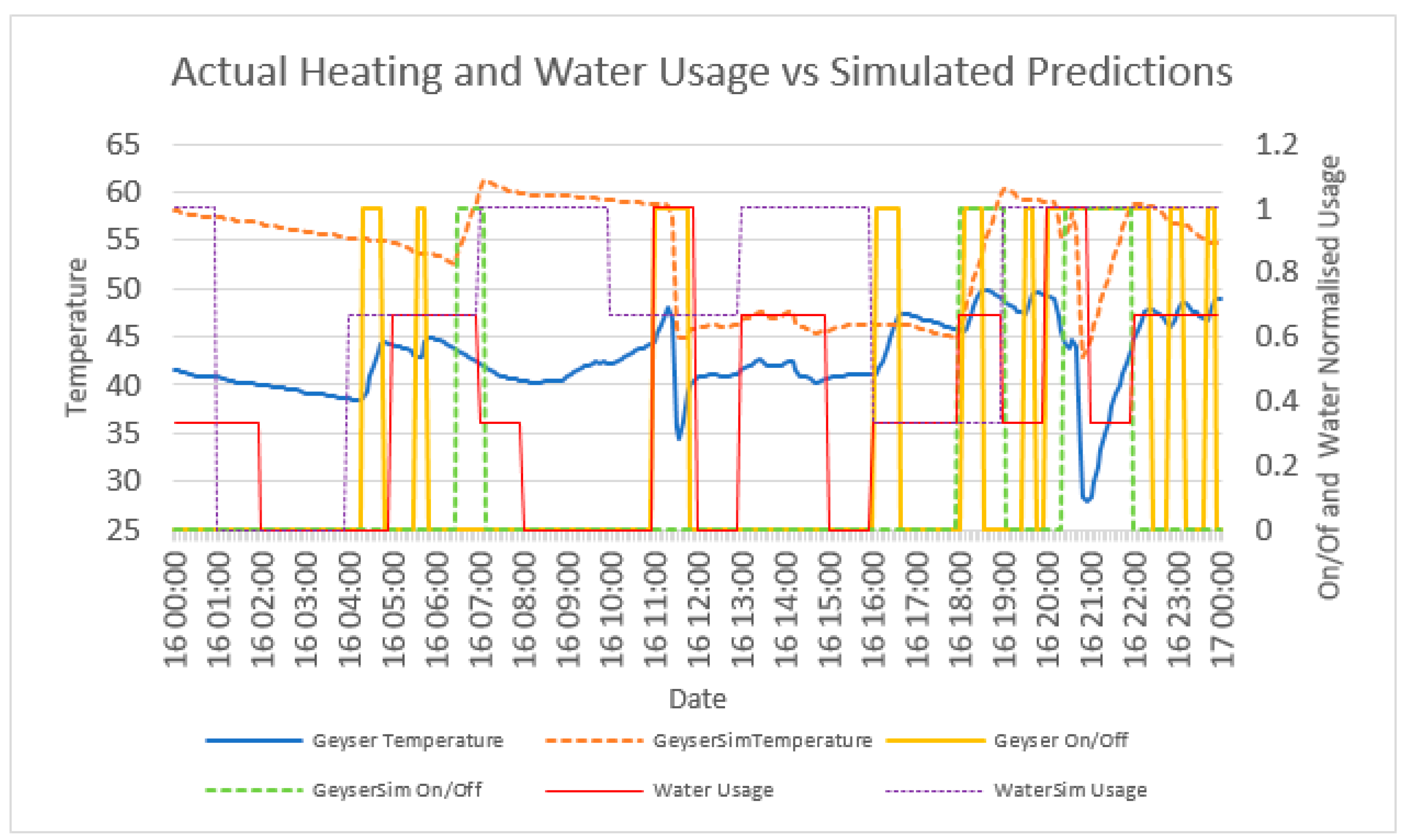
5.1. Profile Solar Geyser Heating
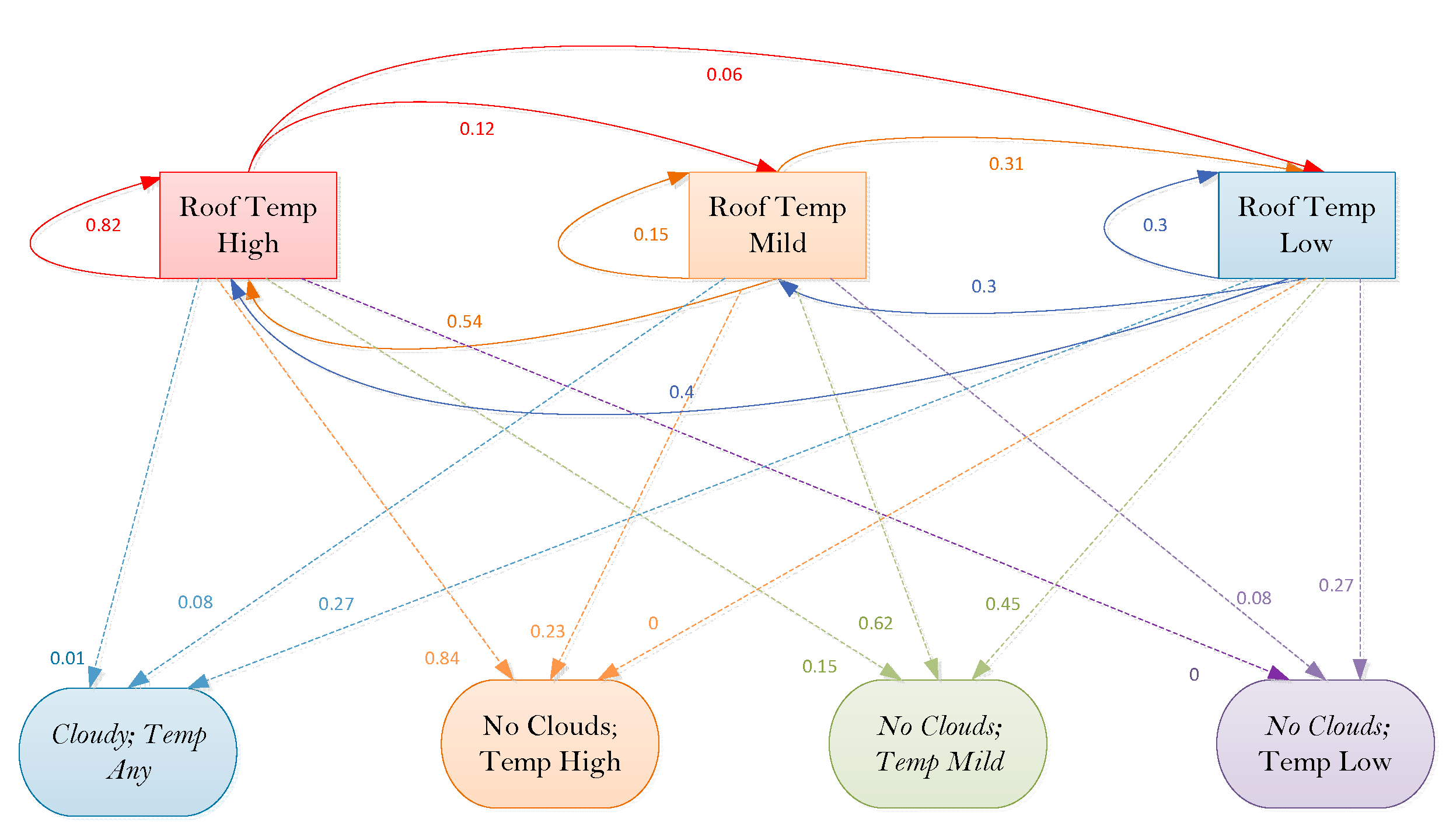
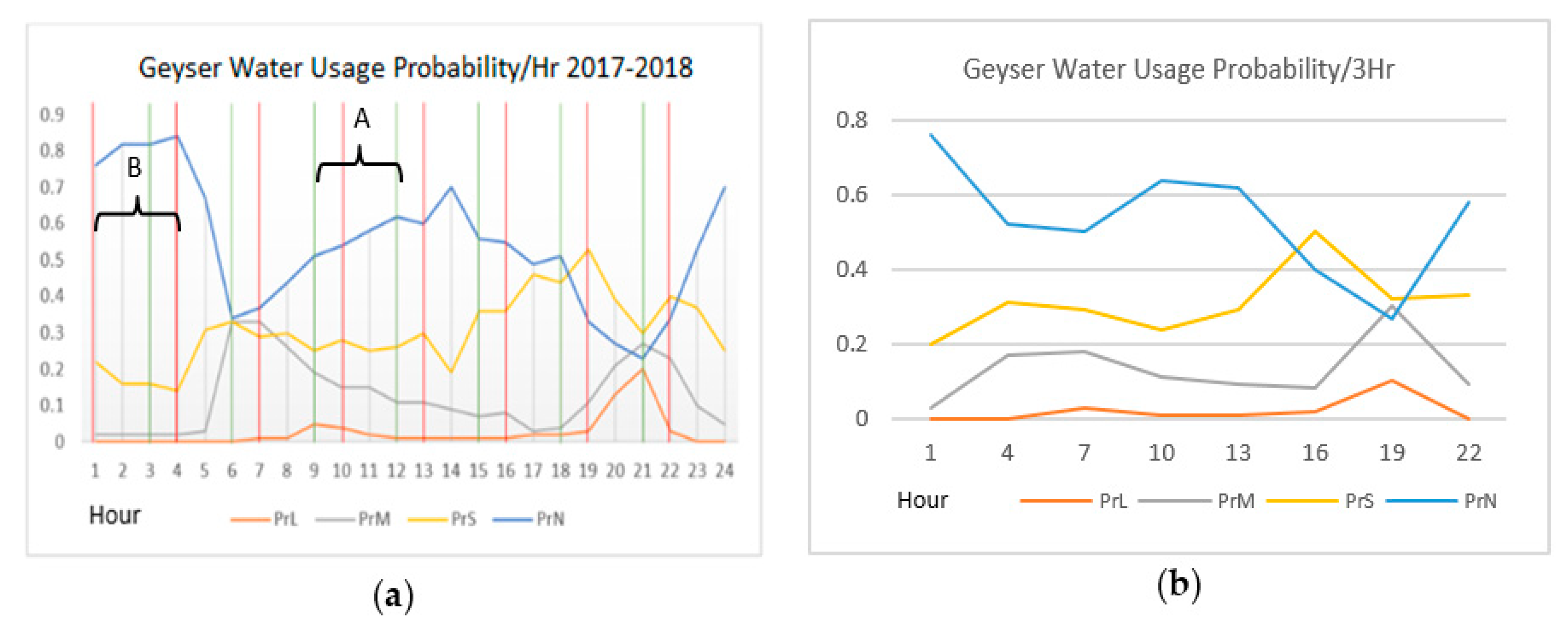
5.2. Warm Water Probabilities
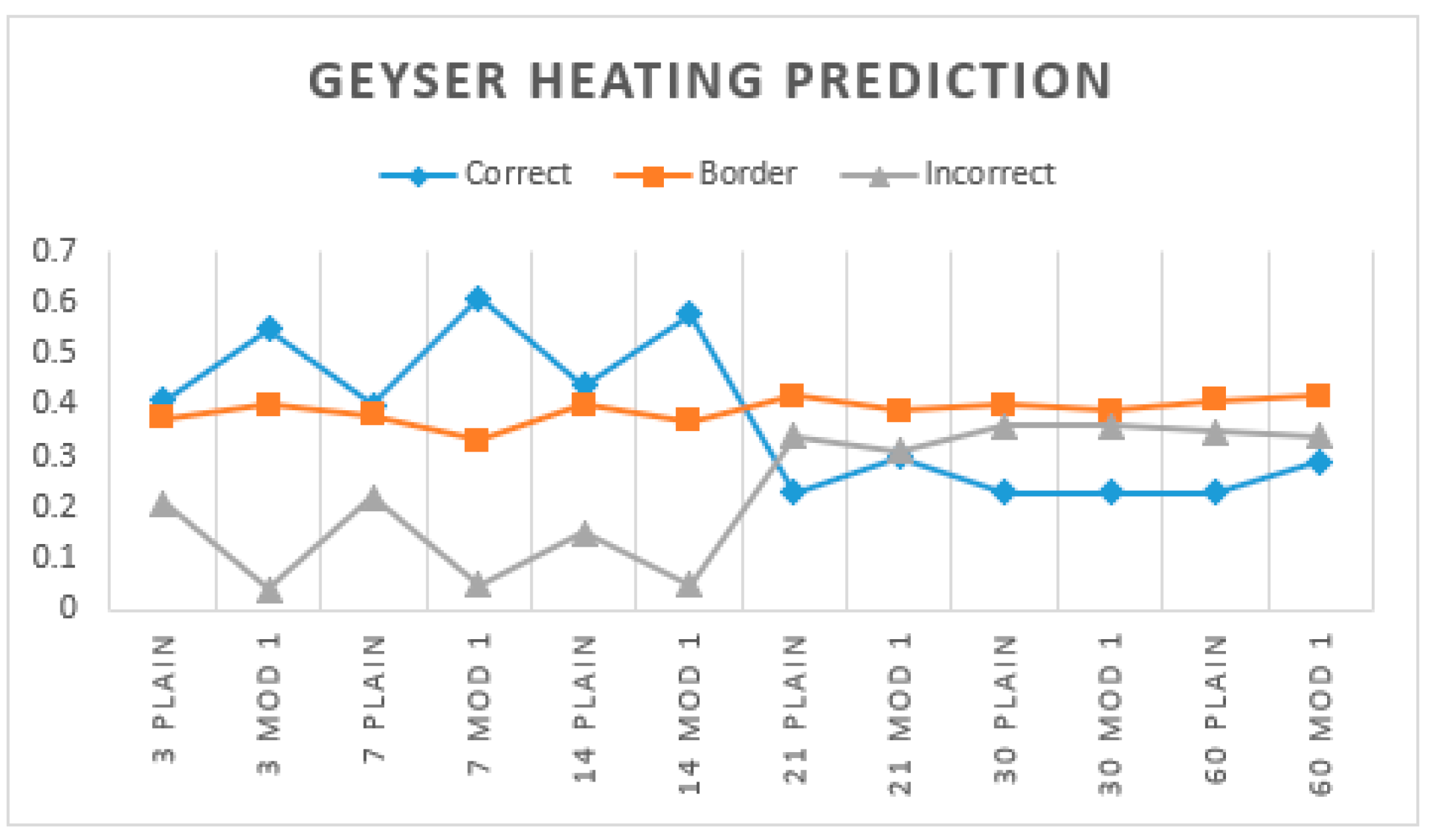
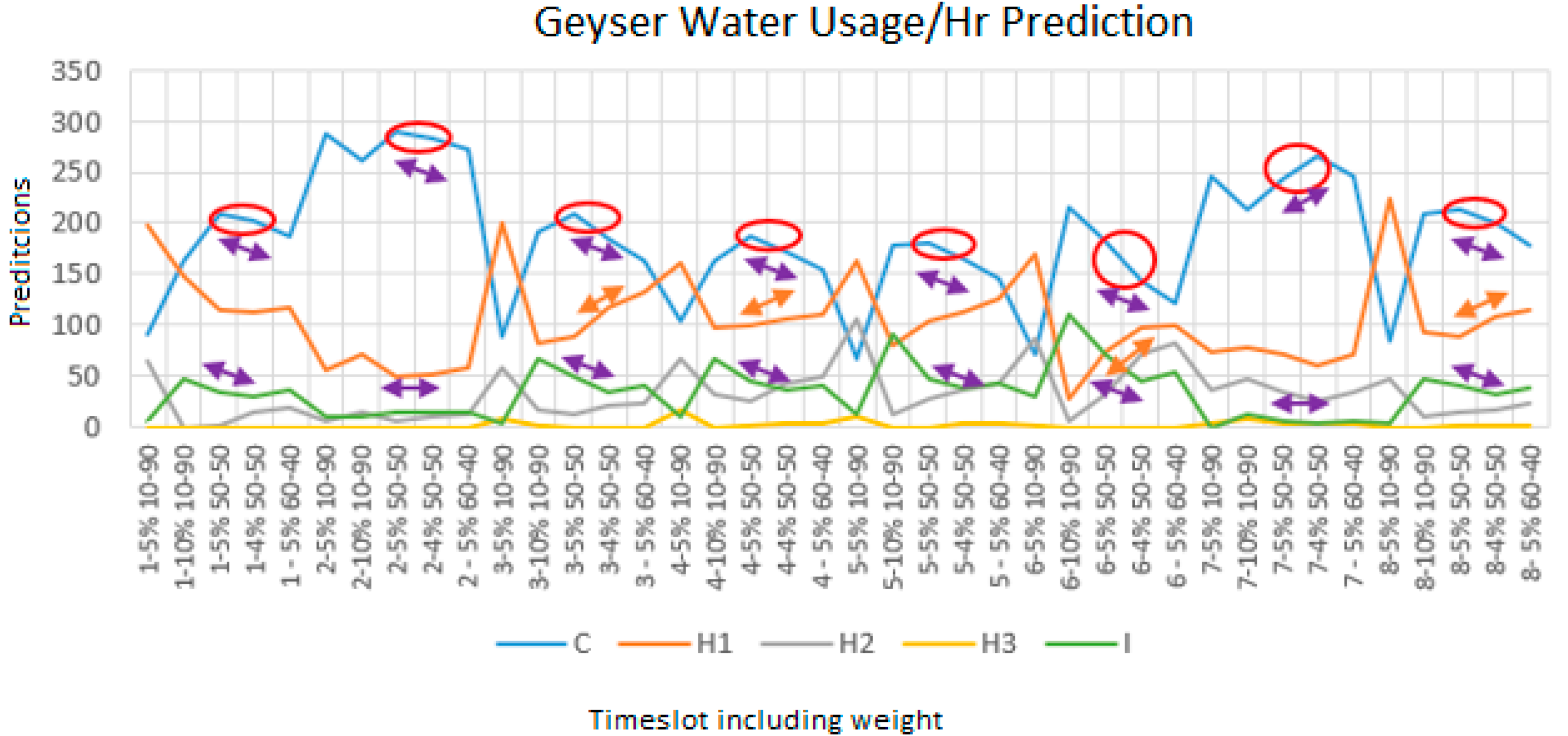
5.3. Combining Water Usage and Solar Heating Predictions for Controlling Geyser Element
- Except for timeslot four to six, no solar heating will be included to determine if geyser element must be enabled.
- For each timeslot, the current and next timeslot minimum temperatures values were retrieved.
- Every five minutes or when temperatures changes, the time-period not elapsed in timeslot and time required to heat water from current temperature to next time slot are calculated.
6. Conclusions
- Converting sensor readings into linguistic terms simplified the prediction.
- Altering the Baum–Welch algorithm by means of the hidden Markov model training by decreasing the length of the observations. Thus making the predictions more accurate through adding different weights to different age emissions and observation data for prediction models where sudden behavioural changes can occur.
- Proving that an artificial algorithm can be implemented in a smart home or office environment with the same comfort levels, but also reducing the electrical power usage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
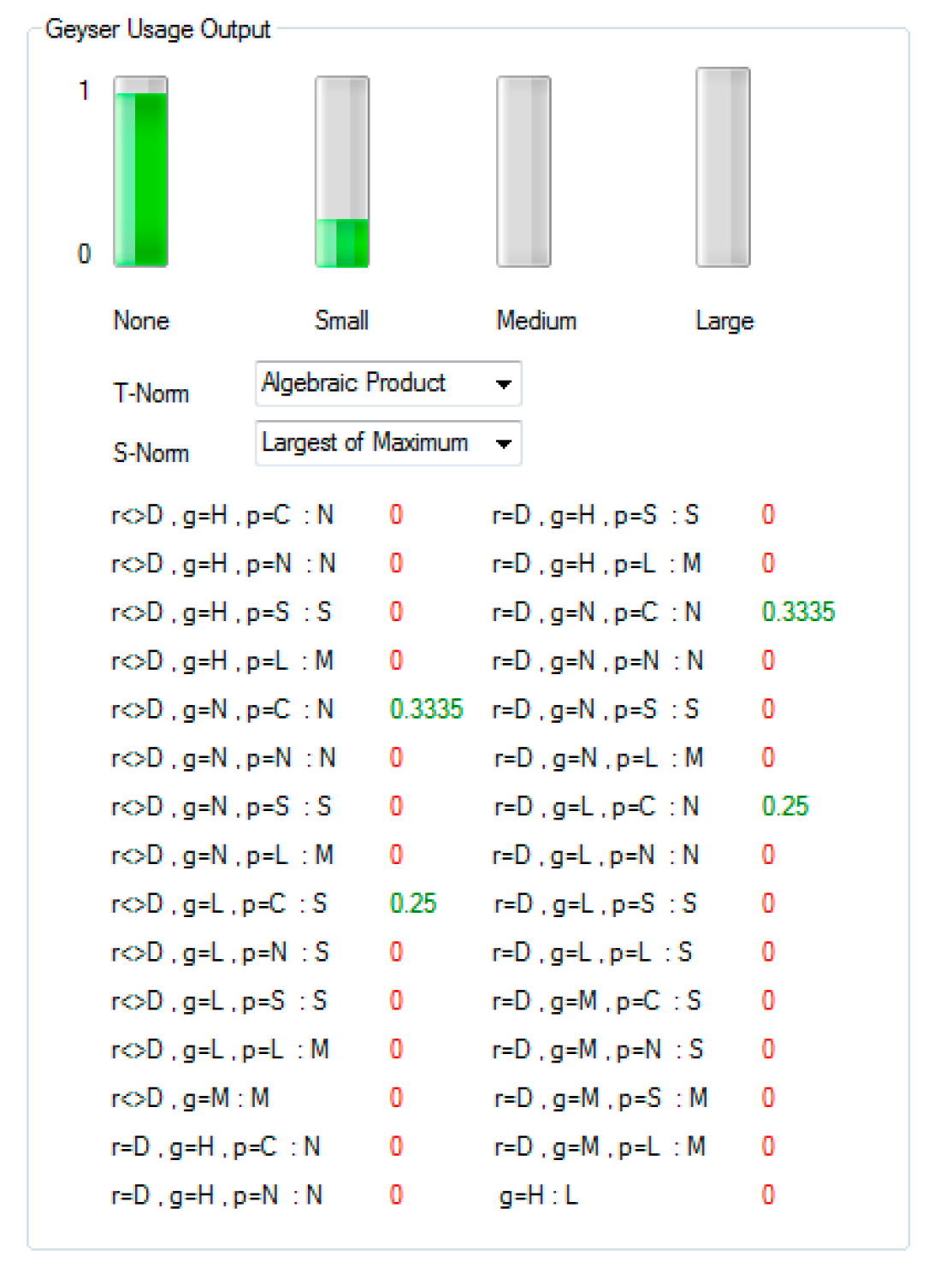
| Rule | DeltaRoof | And DeltaGeyser | And DeltaPipe | Usage |
|---|---|---|---|---|
| 1 | not Drop | Heatup | Cooldown | UseNone |
| 2 | not Drop | Heatup | Normal | UseNone |
| 3 | not Drop | Heatup | SmallRise | UseSmall |
| 4 | not Drop | Heatup | LargeRise | UseMedium |
| 5 | not Drop | Normal | Cooldown | UseNone |
| 6 | not Drop | Normal | Normal | UseNone |
| 7 | not Drop | Normal | SmallRise | UseSmall |
| 8 | not Drop | Normal | LargeRise | UseMedium |
| 9 | not Drop | DropLow | Cooldown | UseSmall |
| 10 | not Drop | DropLow | Normal | UseSmall |
| 11 | not Drop | DropLow | SmallRise | UseSmall |
| 12 | not Drop | DropLow | LargeRise | UseMedium |
| 13 | not Drop | DropMedium | UseMedium | |
| 14 | not Drop | Heatup | Cooldown | UseNone |
| 15 | not Drop | Heatup | Normal | UseNone |
| 16 | not Drop | Heatup | SmallRise | UseSmall |
| 17 | not Drop | Heatup | LargeRise | UseMedium |
| 18 | Drop | Normal | Cooldown | UseNone |
| 19 | Drop | Normal | Normal | UseNone |
| 20 | Drop | Normal | SmallRise | UseSmall |
| 21 | Drop | Normal | LargeRise | UseMedium |
| 22 | Drop | DropLow | Cooldown | UseNone |
| 23 | Drop | DropLow | Normal | UseNone |
| 24 | Drop | DropLow | SmallRise | UseSmall |
| 25 | Drop | DropLow | LargeRise | UseSmall |
| 26 | Drop | DropMedium | Cooldown | UseSmall |
| 27 | Drop | DropMedium | Normal | UseSmall |
| 28 | Drop | DropMedium | SmallRise | UseMedium |
| 29 | Drop | DropMedium | LargeRise | UseMedium |
| 30 | DropHigh | UseLarge |
Appendix B
Appendix C
Appendix D

References
- Rea, M.S.; Figueiro, M.G.; Bierman, A.; Bullough, J.D. Circadian light. J. Circadian Rhythm 2010, 8, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bea, S.; Fang, M.Z.; Rustgi, V.; Zarbl, H.; Androulakis, I.P. At the interface of lifestyle, behaviour, and Circadian Rhythms: Metabolic Implications. Front. Nutr. 2019, 6, 2. [Google Scholar]
- Dintchev, O.D. Solar Water Heating as a Mechanism to Reduce Domestic Electrical Energy Consumption and Its Contribution towards South African Maximum Demand. In Proceedings of the 15th Domestic Use of Electrical Energy Conference, Cape Town, South Africa, 30 March–1 April 2006. [Google Scholar]
- Sauer, F.J. Predicting Solar Radiation Based on Available Weather Indications. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2013. [Google Scholar]
- Delport, J. The Influence of Temperature on Residential Hot Water Load Control. In Proceedings of the 15th Domestic Use of Electrical Energy Conference, Cape Town, South Africa, 30 March–1 April 2006; pp. 2–3. [Google Scholar]
- LaMeres, B.J.; Nehvir, M.H.; Gerez, V. Controlling the average residential electric water heater power demand using fuzzy logic. Electr. Power Syst. Res. 1999, 52, 267–271. [Google Scholar] [CrossRef]
- Catherin, Q.S. Effective Geyser Management through Intelligent Hot Water Usage Profiling. Master’s Degree, Cape Peninsula University of Technology, Cape Town, South Africa, December 2009; pp. 51–56. [Google Scholar]
- Bakker, V.; Molderink, A.; Hurink, J. Domestic heat demand prediction using neural networks. In Proceedings of the 9th International Conference of System Engineering, Auckland, New Zealand, 1–3 September 2008; pp. 189–194. [Google Scholar]
- Hohne, P.A.; Kusakane, K.; Numbi, B.P. A review of water heating technologies: An application to the African context. Energy Rep. 2019, 5, 3. [Google Scholar] [CrossRef]
- Thomas, R.S.M.; Xia, X.; Zhang, J.F. Energy Efficient Geyser. In Proceedings of the 17th Domestic Use of Electrical Energy Conference, Cape Town, South Africa; 2008; pp. 3–6. [Google Scholar]
- Wolter, N.; Carrim, M.; Cohen, C.; Tempia, S.; Walaza, S.; Cohen, C.; Sibongile, W.; Sahr, P.; Gouveia, L.; Treurnicht, F.; et al. Legionnaires’ disease in South Africa 2012–2014. Emerg. Infect. Dis. 2016, 22, 131–133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- World Health Organisation. Legionella and the Prevention of Legionellosis; WHO: Geneva, Switzerland, 2007; p. 30. [Google Scholar]
- Geyserwise. Available online: http://geyserwise.com (accessed on 24 March 2019).
- Delport, J. The geyser gadgets that work/do not work. In Proceedings of the 14th Domestic Use of Electrical Energy Conference, Cape Town, South Africa, 29 March–2 April 2005; p. 3. [Google Scholar]
- Tooley, M.; Tooley, R. Exploring the Arduino Part 12: Wi-Fi and the Internet of Things. In Everyday Practical Electronics; Wimborne Publishing: Wimborne, UK, 2017; p. 41. [Google Scholar]
- ESP Basic. Available online: www.esp8266basic.com (accessed on 3 June 2018).
- Chen, G.; Pham, T.T. Introduction to Fuzzy Sets. In Fuzzy Logic and Fuzzy Control Systems; CRC Press: Houston, TX, USA, 2001; pp. 147–149. [Google Scholar]
- Fuzzylite. Available online: https://Fuzzylite.com (accessed on 19 May 2019).
- Galindo, José, G. Fuzzy Databases: Modelling, Design and Implementation; Idea Group Publishing: London, UK, 2006; pp. 4–5. [Google Scholar]
- Thaker, S.; Nagori, V. Analysis of Fuzzification Process in Fuzzy Expert Systems. In Proceedings of the International Conference on Computer Intelligence and Data Science, Haryana, India, 7–8 April 2018; pp. 1308–1316. [Google Scholar]
- Lee, K.H. First Course on Fuzzy Theory and Applications; Springer: New York, NY, USA, 2005; pp. 254–269. [Google Scholar]
- Reynolds, A.P.; Richards, G.; de la Iglesias, B.; Rayward-Smith, V.J. Clustering Rules: A Comparison of Partitioning and Hierarchical Clustering Algorithm. J. Math. Model. Algorithms 2006, 5, 475–504. [Google Scholar] [CrossRef]
- Swarndeep, S.J.; Pandya, S. An Overview of Partitioning Algorithms in Clustering Techniques. Int. J. Adv. Res. Comput. Eng. Technol. 2020, 5, 1945. [Google Scholar]
- Liu, T.; Lemeire, J. Efficient and Effective Learning of HMMs Based on Identification of Hidden States. Hindawi Math. Probl. Eng. 2017, 2017, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Schliep, A. A Bayesian Approach to Learning Hidden Markov Model Topology with Biological Sequence Analysis. PhD Thesis, Faculty of Mathematics and Science, University of Cologne, Düsseldorf, Germany, 2002; pp. 19–23. [Google Scholar]
- Rabiner, L.R. A tutorial on Hidden Markov Models and selected applications in speech recognition. Proc. IEEE 1989, 77, 7–12. [Google Scholar] [CrossRef]
- Pietrykowski, M.; Salabun, W. Applications of Hidden Markov Model: State-of-the-art. Wojciech Salabun Et Alint. J. Comput. Technol. Appl. 2014, 5, 1384–1391. [Google Scholar]
- Pulford, G.W. Multihypthesis Viterbi Data Association: Algorithm Development and Assessment. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 583–584. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Juang, B.H. An Introduction to Hidden Markov Model. IEEE ASSP Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Cappé, O.; Moulines, E.; Rydén, T. Main Definitions and Notations. In Inference in Hidden Markov Models; Springer: Berlin/Heidelberg, Germany, 2007; pp. 35–47. [Google Scholar]
- Li, C.; Biswas, G.; Dale, M.; Dale, P. Building models of ecological dynamics using hmm based temporal data clustering. In Proceedings of the Fourth International Conference on Intelligent Data Analysis, Cascais, Portugal, 13–15 September 2001; pp. 54–55. [Google Scholar]
- Soiman, S.; Rusu, I.; Pentiuc, S. Optimizing the Forward Algorithm for Hidden Markov Model on IBM Roadrunner clusters. Adv. Electr. Comput. Eng. 2015, 15, 103–108. [Google Scholar] [CrossRef]
- Downey, A.B. Think Bayes; Green Tea Press: Needham, MA, USA, 2012; pp. 2–4. [Google Scholar]
- Melikyan, Z.; Egnatosyan, S. Developing of New Structure of Flat Plate Solar Water and Method for Calculation and Design. Int. J. Energy Power Eng. 2016, 5, 143. [Google Scholar] [CrossRef] [Green Version]
- Razael, V.; Pezeshk, H.; Perez-Sanchez, H. Generalized Baum-Welch Algorithm Based on the Similarity between Sequences. PLoS ONE 2013, 8, e80565. [Google Scholar]







| Device | Description |
|---|---|
| NodeMCU ESP8266-12E | 1 ADC and multiple general function ports with 2.4Ghz 802.11 b/g/n wireless standard, flashed with ESP8266-basic [15,16]. |
| LM4052 | 4 Port Analogue Multiplexer for Current and Temperature Sensors. |
| Yhdc Non-Invasive clip-on current sensor | 30A/1V Current monitor confirm Element status as illustrated in Figure 3a. |
| 3xLM317 temperature sensors | Recording geyser or Pool water temperatures. |
| H105F-1 SPST relay | Maximum contact current of 40A and average resistive load of 30A@240V AC. |
| Description | Type ID | Direction | AnaDig | Group |
|---|---|---|---|---|
| TempGeyserInside | 1 | I | A | Geyser |
| TempGeyserOutside | 2 | I | A | Geyser |
| TempGeyserPipe | 3 | I | A | Geyser |
| CurrentGeyser | 30 | I | A | Geyser |
| Relay Geyser | 100 | O | A | Geyser |
| Pool Temp Inside | 4 | I | A | Pool |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Bruyn, D.N.; Kotze, B.; Hurst, W. A Hidden Markov Model and Fuzzy Logic Forecasting Approach for Solar Geyser Water Heating. Infrastructures 2021, 6, 67. https://doi.org/10.3390/infrastructures6050067
de Bruyn DN, Kotze B, Hurst W. A Hidden Markov Model and Fuzzy Logic Forecasting Approach for Solar Geyser Water Heating. Infrastructures. 2021; 6(5):67. https://doi.org/10.3390/infrastructures6050067
Chicago/Turabian Stylede Bruyn, Daniel N., Ben Kotze, and William Hurst. 2021. "A Hidden Markov Model and Fuzzy Logic Forecasting Approach for Solar Geyser Water Heating" Infrastructures 6, no. 5: 67. https://doi.org/10.3390/infrastructures6050067
APA Stylede Bruyn, D. N., Kotze, B., & Hurst, W. (2021). A Hidden Markov Model and Fuzzy Logic Forecasting Approach for Solar Geyser Water Heating. Infrastructures, 6(5), 67. https://doi.org/10.3390/infrastructures6050067








