Determination of Shear Capacity for Load Rating of Concrete Bridges to AS 5100.7-2017
Abstract
:1. Introduction
2. Background
2.1. Load Rating
2.2. Consideration of Shear Action and Shear Capacity
2.2.1. Effect of Proportional Loading Approach on the Load Rating of New Bridges
2.2.2. Shear Load Rating and Load Effects
2.2.3. Ultimate Shear Capacity for Load Rating
3. Present Approach to Shear Load Rating
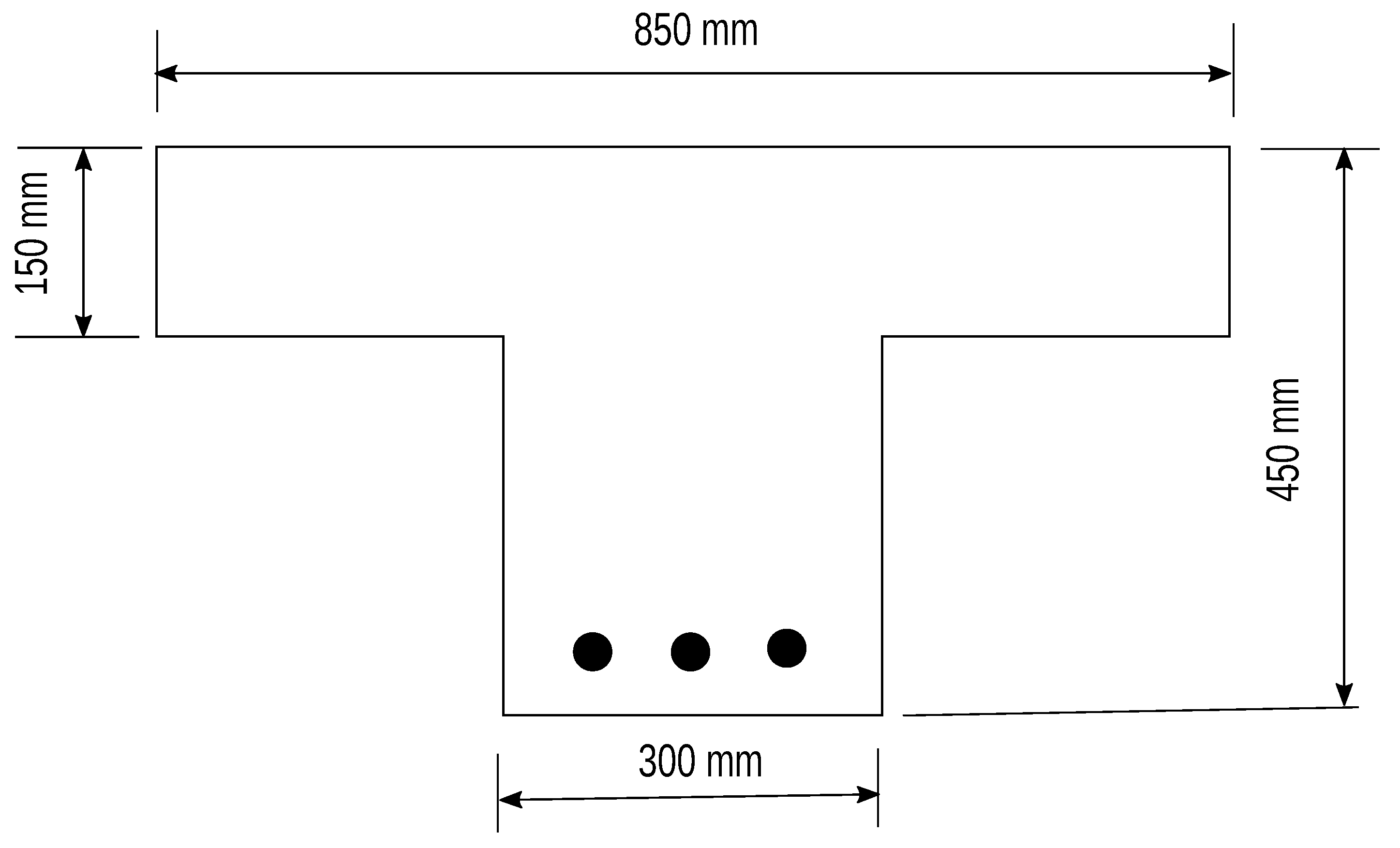
3.1. Analysis
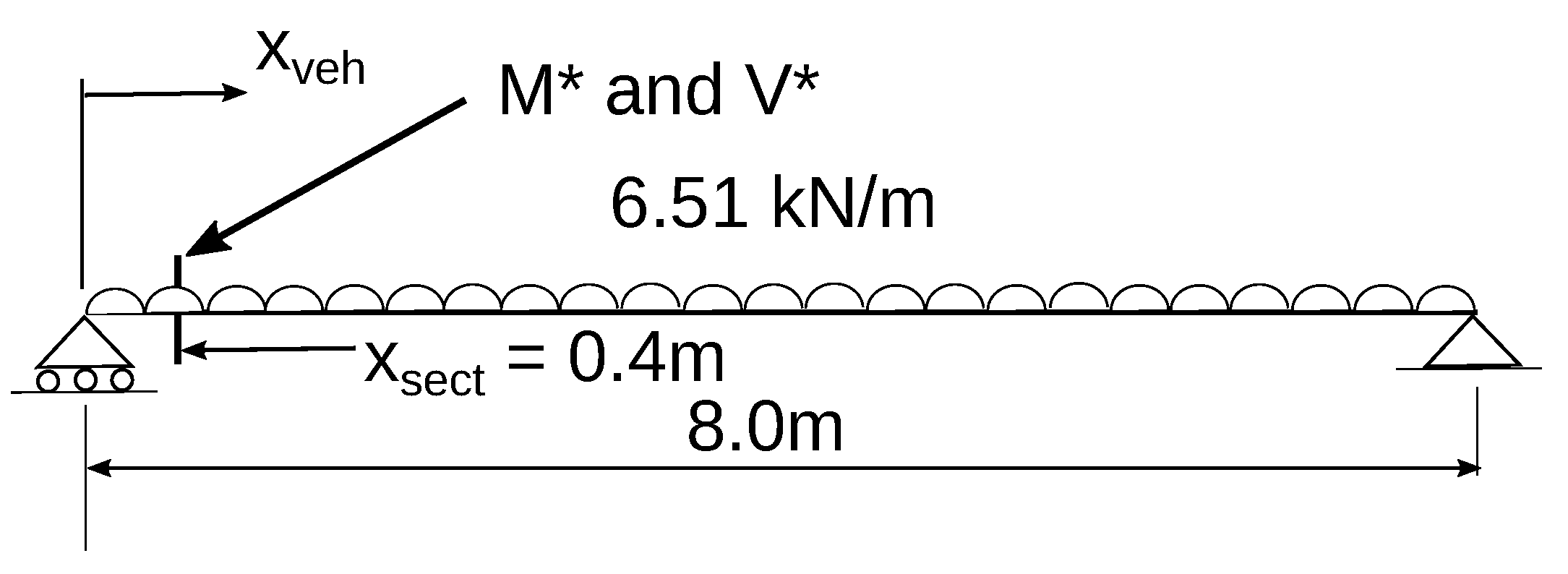
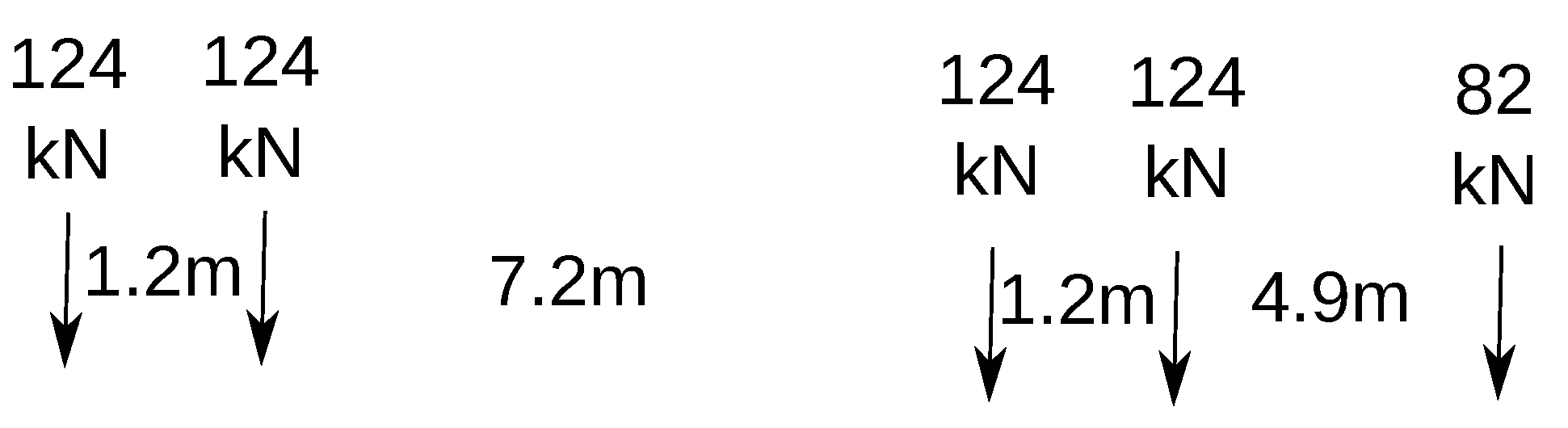
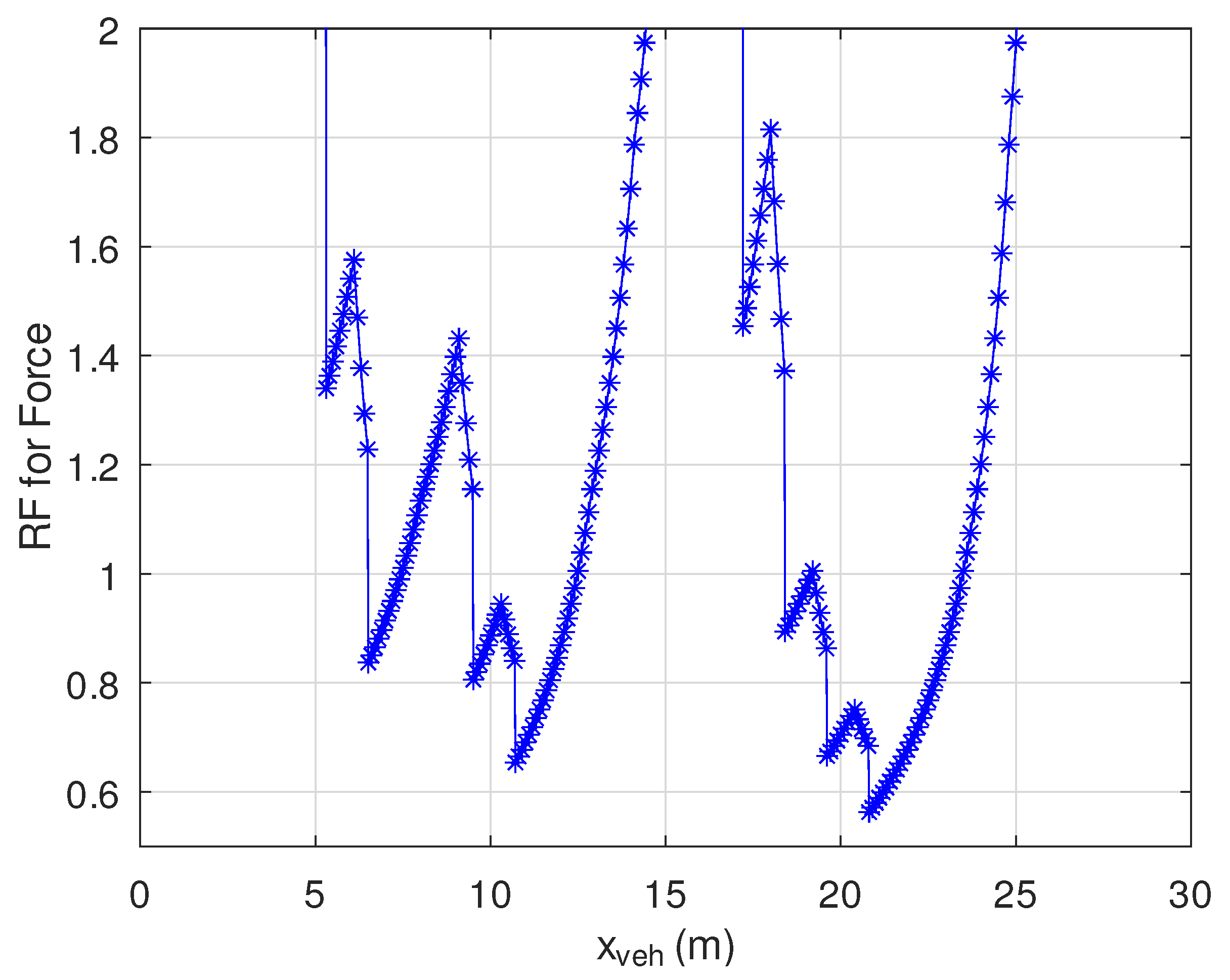
3.2. Load Effects from a Moving Vehicle
4. Recommendation for Load Rating to Consider the Failure Mode Due to Yielding for Axial Forces in Longitudinal Steel
5. Automating Load Rating of Shear
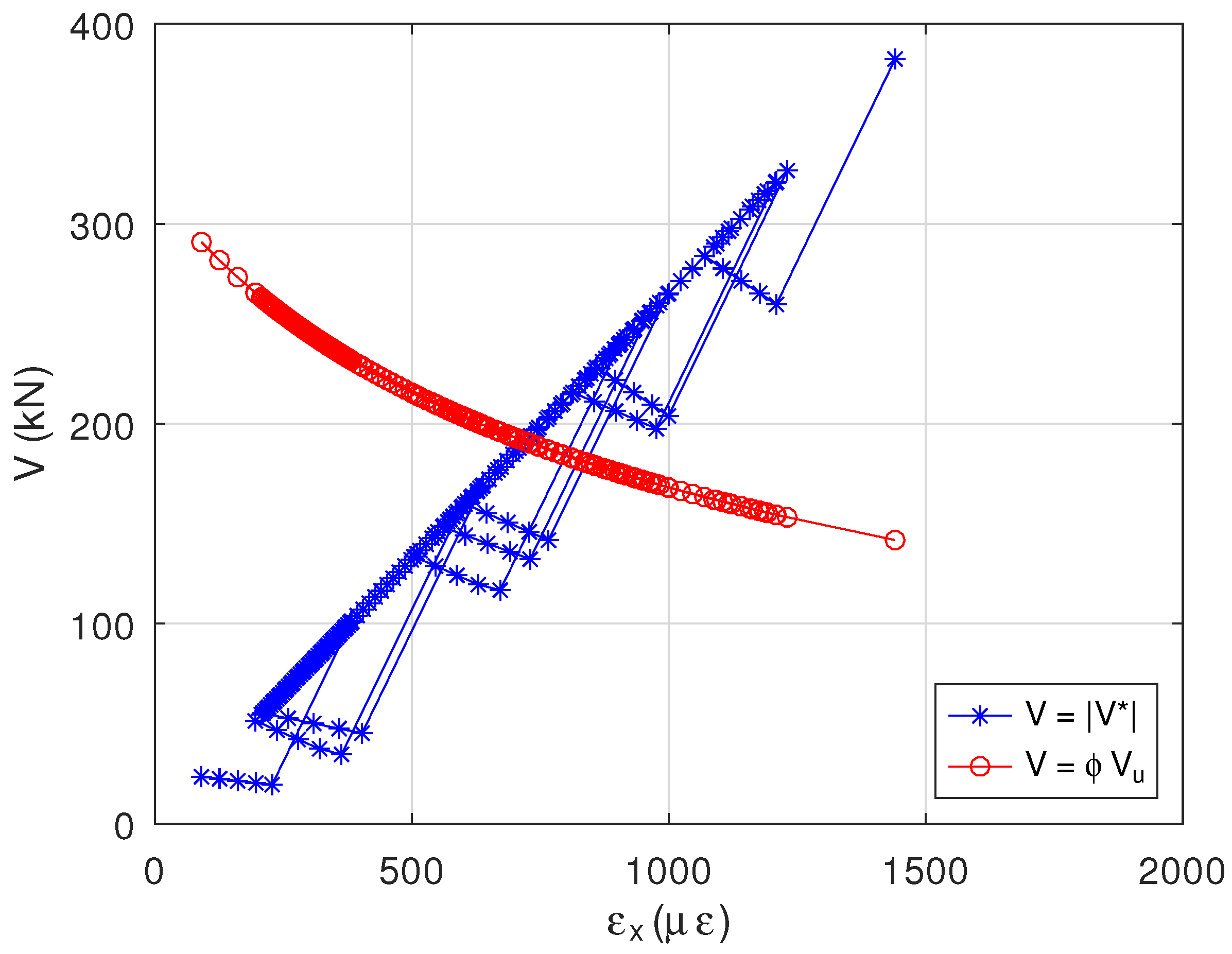
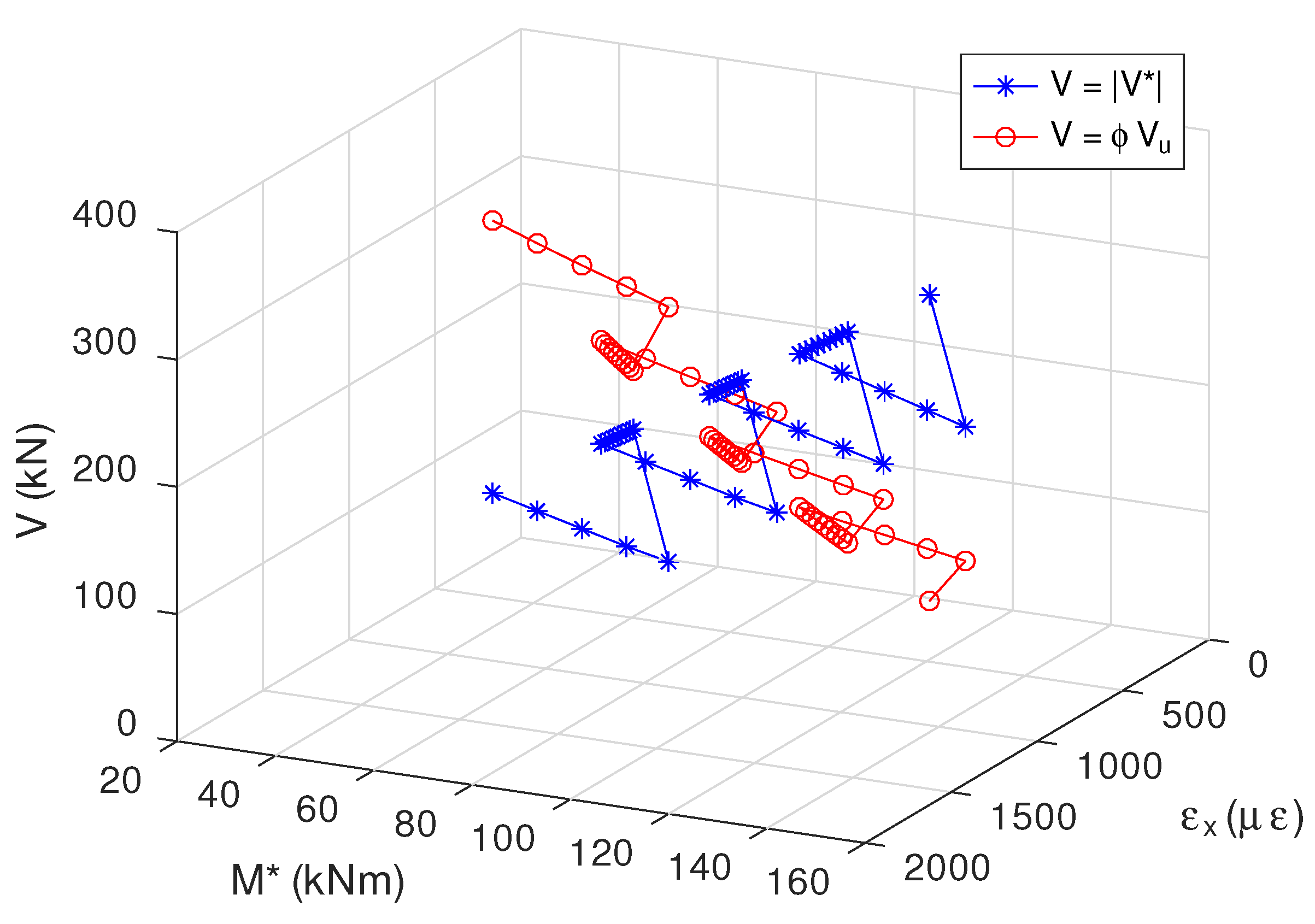
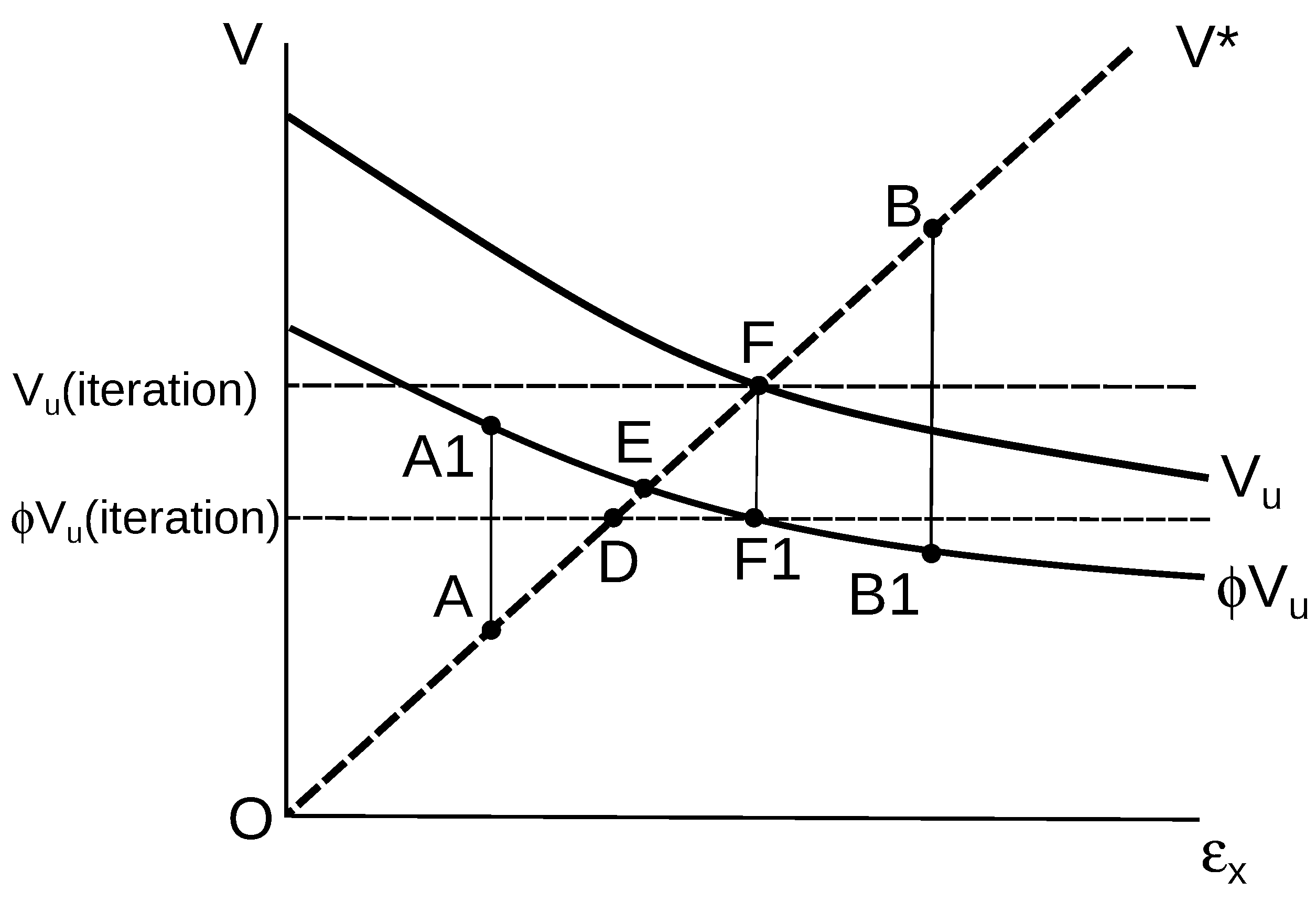
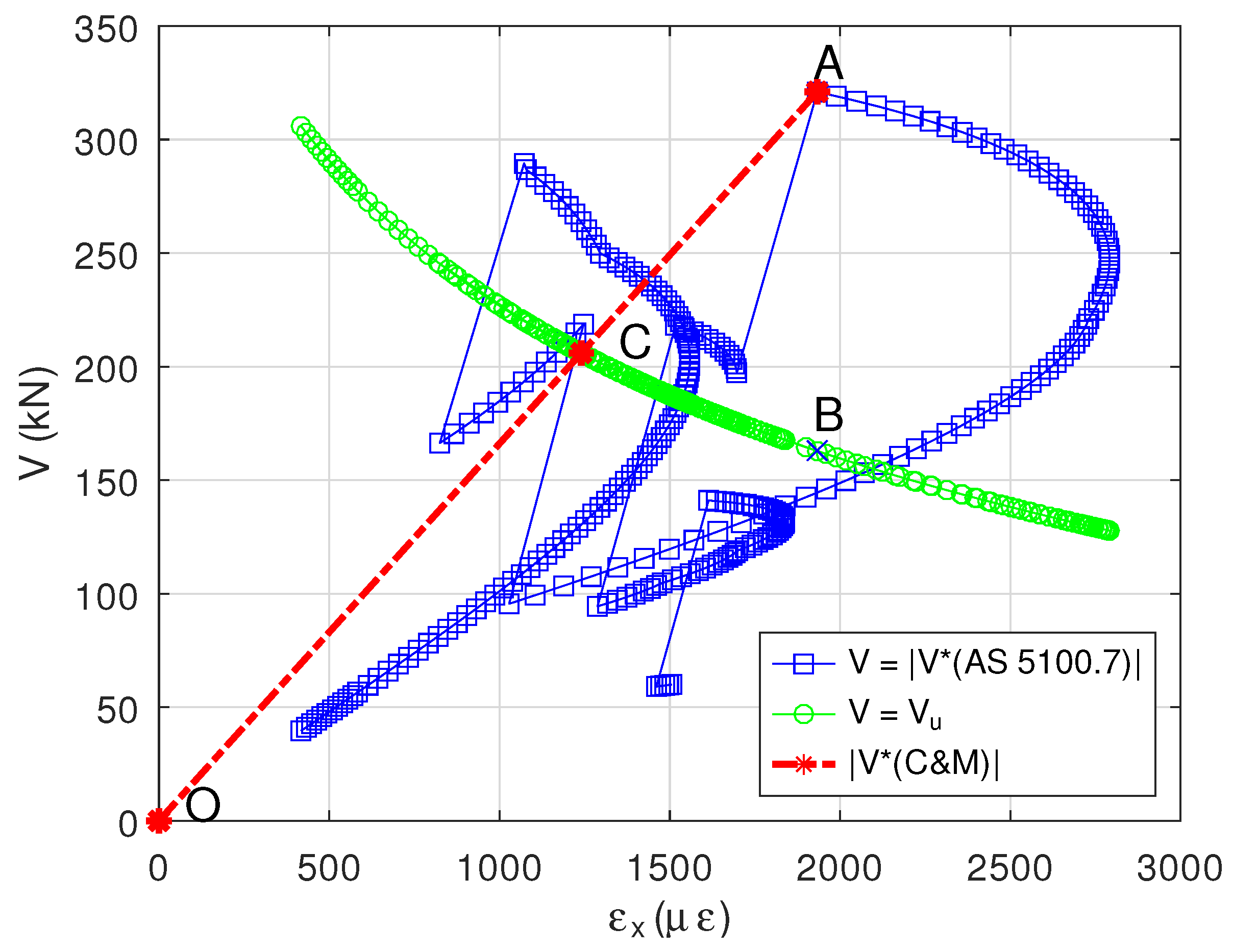
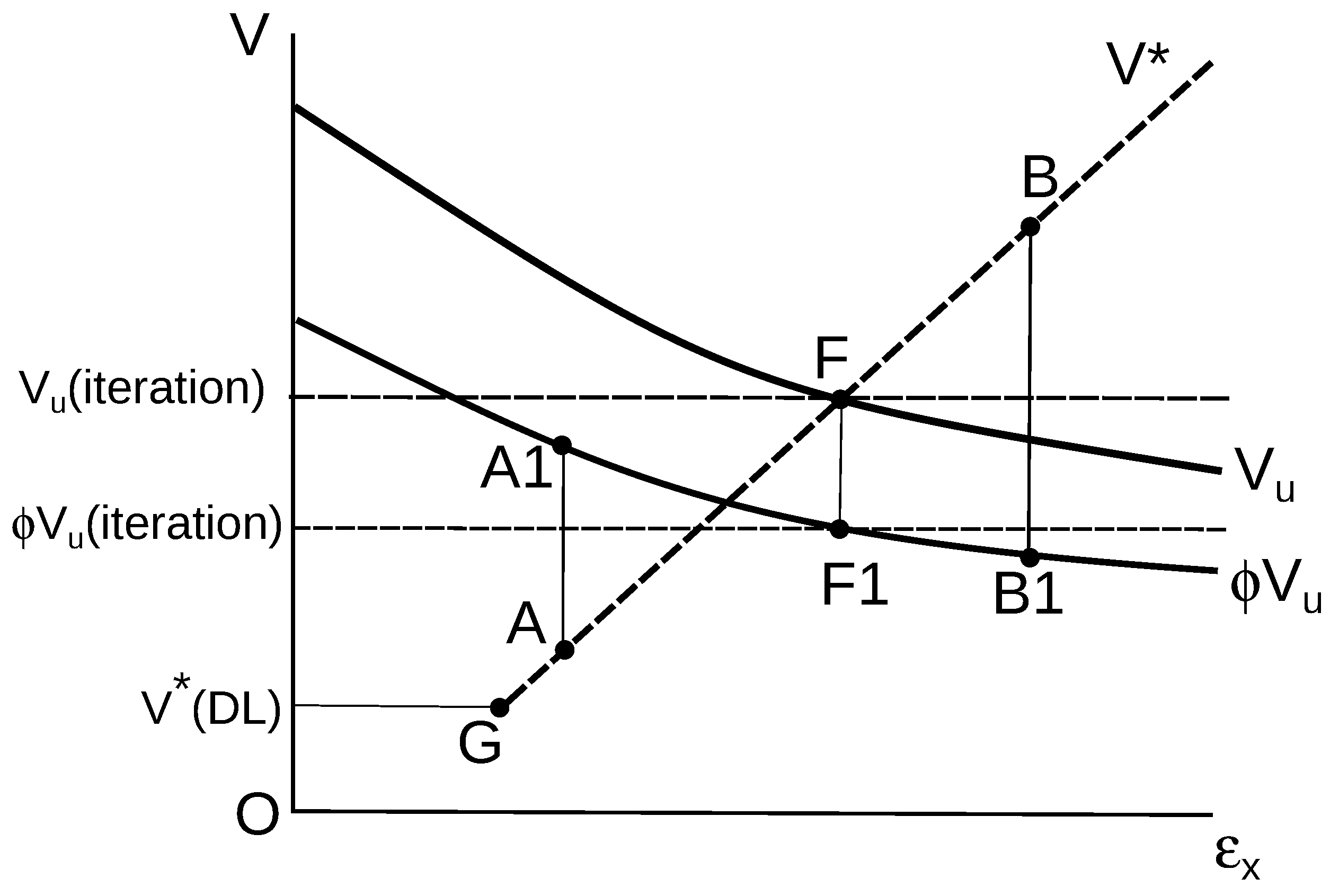
6. Adverse Effects of Using Iteration to Determine the Shear Capacity for Vehicle Load Rating
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Determination of Load Rating Factors
References
- AASHTO. Manual for Bridge Evaluation, 3rd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2018. [Google Scholar]
- CSA-S6-19; Canadian Highway Bridge Design Code. Canadian Standards Association: Mississauga, ON, Canada, 2019.
- AS 5100.5; Bridge Design Part 5: Concrete (with 2018 amendments). Standards Australia: Sydney, NSW, Australia, 2017.
- AS 5100.7; Bridge Design Part 7: Bridge Assessment. Standards Australia: Sydney, NSW, Australia, 2017.
- Caprani, C.C.; Melhem, M.M. On the use of MCFT per AS 5100.5 for the assessment of shear capacities of existing structures. Aust. J. Struct. Eng. 2019, 21, 53–63. [Google Scholar] [CrossRef]
- Holt, J.; Garcia, U.; Waters, S.; Monopolis, C.; Zhu, A.; Bayrak, O.; Powell, L.; Halbe, K.; Kumar, P.; Chavel, B. Concrete Bridge Shear Load Rating; Synthesis Report; Federal Highway Administration; U.S. Department of Transport: Washington, DC, USA, 2018.
- Collins, M.P.; Mitchell, D. Shear design and evaluation of concrete structures. Concr. Aust. 2014, 40, 28–38. [Google Scholar]
- Zheng, L.; Huo, X.S.; Hayworth, R.P. Comparison of load factor rating (LFR) to load and resistance factor rating (LRFR) of prestressed concrete I-beam bridges. In Proceedings of the Structures Congress 2007, Long Beach, CA, USA, 16–19 May 2007. [Google Scholar]
- AS 3600; Concrete Structures (with 2018 and 2021 Amendments). Standards Australia: Sydney, NSW, Australia, 2018.
- AASHTO. AASHTO LRFD Bridge Design Specification, 9th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- Main Roads Western Australia. Bridge Branch Design Information Manual. Version 7, Document Reviewed 2022. Available online: https://www.mainroads.wa.gov.au/technical-commercial/technical-library/ (accessed on 31 October 2022).
- Main Roads Western Australia. Structures Engineering Design Manual. Document No. 3912 /03, Document Reviewed 2014. Available online: https://www.mainroads.wa.gov.au/technical-commercial/technical-library/ (accessed on 31 October 2022).
- Holt, J.; Bayrak, O.; Okumus, P.; Stavridis, A.; Murphy, T.; Panchal, D.; Dutta, A.; Randiwe, A. Concrete Bridge Shear Load Rating Guide and Examples Using the Modified Compression Field Theory; Technical Report; Federal Highway Administration; U.S. Department of Transport: Washington, DC, USA, 2022. [Google Scholar]
- Python. Available online: https://www.python.org/ (accessed on 31 October 2022).
- Hibbeler, R.C. Structural Analysis, SI ed.; Prentice Hall, Pearson Education South Asia Pte Ltd.: Singapore, 2002; pp. 443–457. [Google Scholar]
- Matplotlib: Visualization with Python. Available online: https://matplotlib.org/ (accessed on 31 October 2022).
- GNU Octave Scientific Programming Language. Available online: https://octave.org/ (accessed on 31 October 2022).
- Ahmad, A.; Warner, R.F. Ductility Requirements for Continuous Reinforced Concrete Structures; Research Report No. R62; Department of Civil Engineering, University of Adelaide: Adelaide, SA, Australia, 1984. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wong, K.W.; Vimonsatit, V. Determination of Shear Capacity for Load Rating of Concrete Bridges to AS 5100.7-2017. Infrastructures 2022, 7, 156. https://doi.org/10.3390/infrastructures7110156
Wong KW, Vimonsatit V. Determination of Shear Capacity for Load Rating of Concrete Bridges to AS 5100.7-2017. Infrastructures. 2022; 7(11):156. https://doi.org/10.3390/infrastructures7110156
Chicago/Turabian StyleWong, Koon Wan, and Vanissorn Vimonsatit. 2022. "Determination of Shear Capacity for Load Rating of Concrete Bridges to AS 5100.7-2017" Infrastructures 7, no. 11: 156. https://doi.org/10.3390/infrastructures7110156
APA StyleWong, K. W., & Vimonsatit, V. (2022). Determination of Shear Capacity for Load Rating of Concrete Bridges to AS 5100.7-2017. Infrastructures, 7(11), 156. https://doi.org/10.3390/infrastructures7110156







