Effect of Directional Added Mass on Highway Bridge Response during Flood Events
Abstract
:1. Introduction
2. Materials and Methods
2.1. Acoustic Domain Theory
2.2. Coupling Solid and Acoustic Domains
2.3. Essential Boundary Conditions
2.3.1. Imposed Pressure (Dirichlet BCs)
2.3.2. Imposed Kinematics (Neumann BCs)
2.3.3. Imposed Impedance or Admittance (Robin BCs)
3. Numerical and Experimental Implementation
3.1. Prototype Bridge Models
3.2. Small-Scale Physical Model
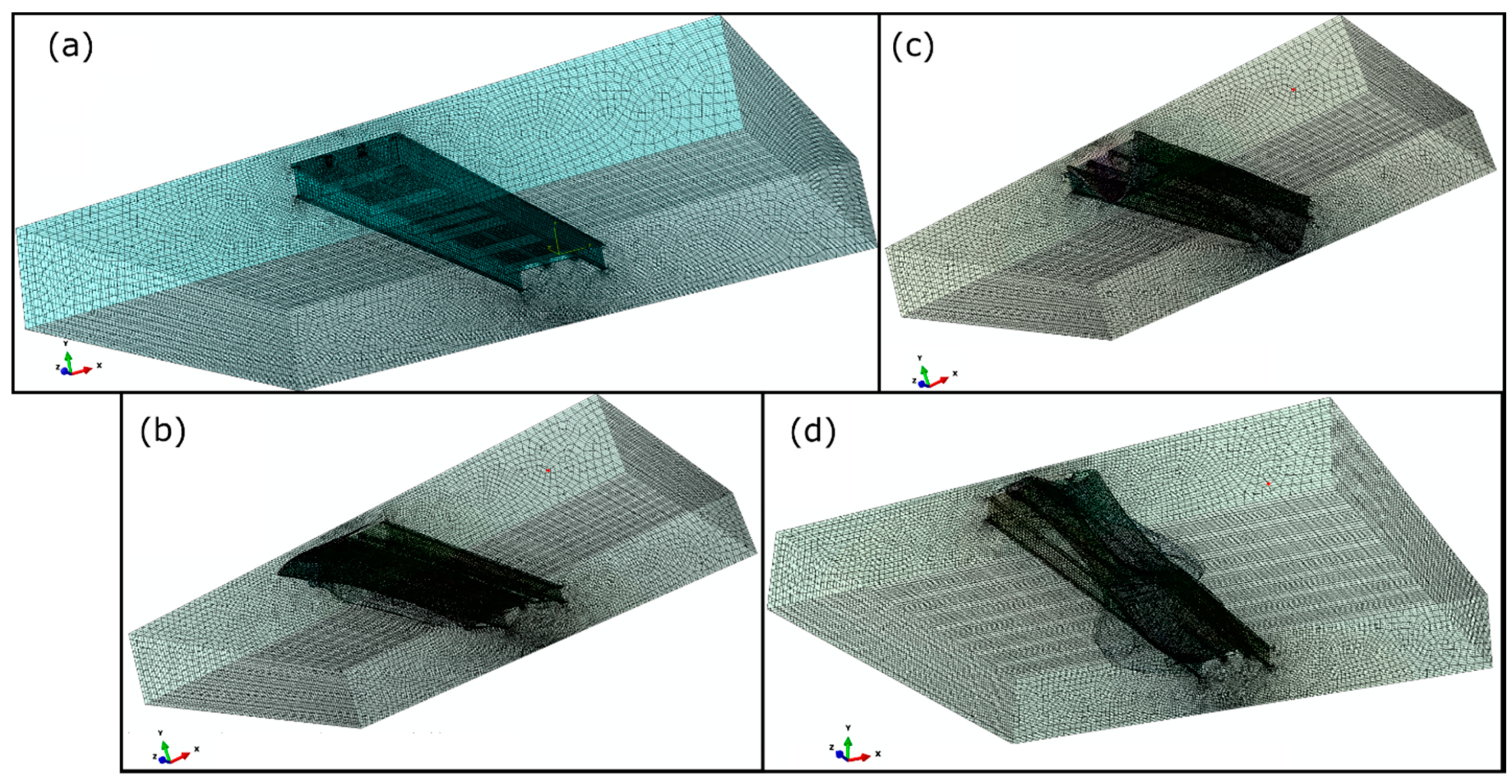
3.3. Numerical CAS Implementation
3.4. Experimental CAS and Data Collections
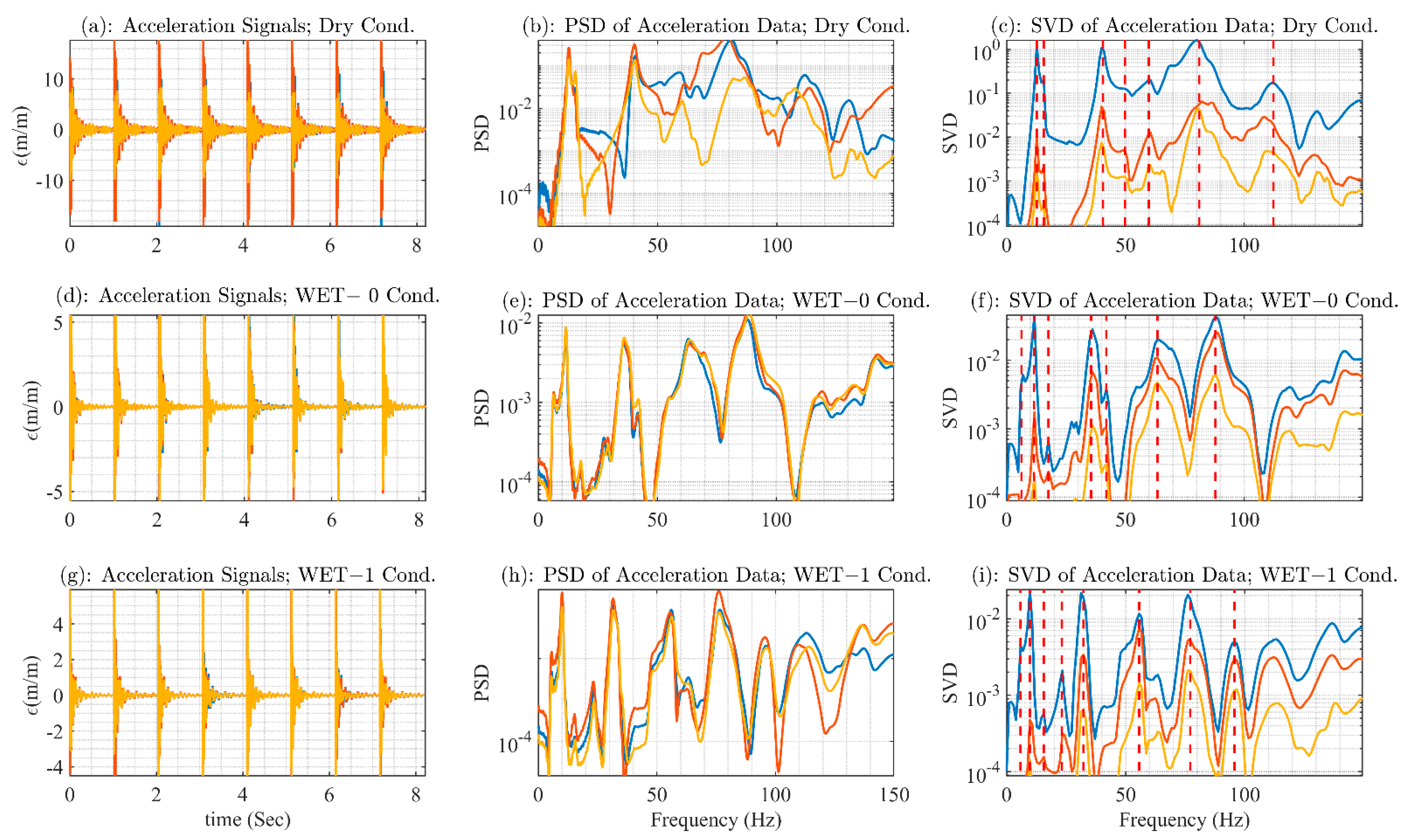
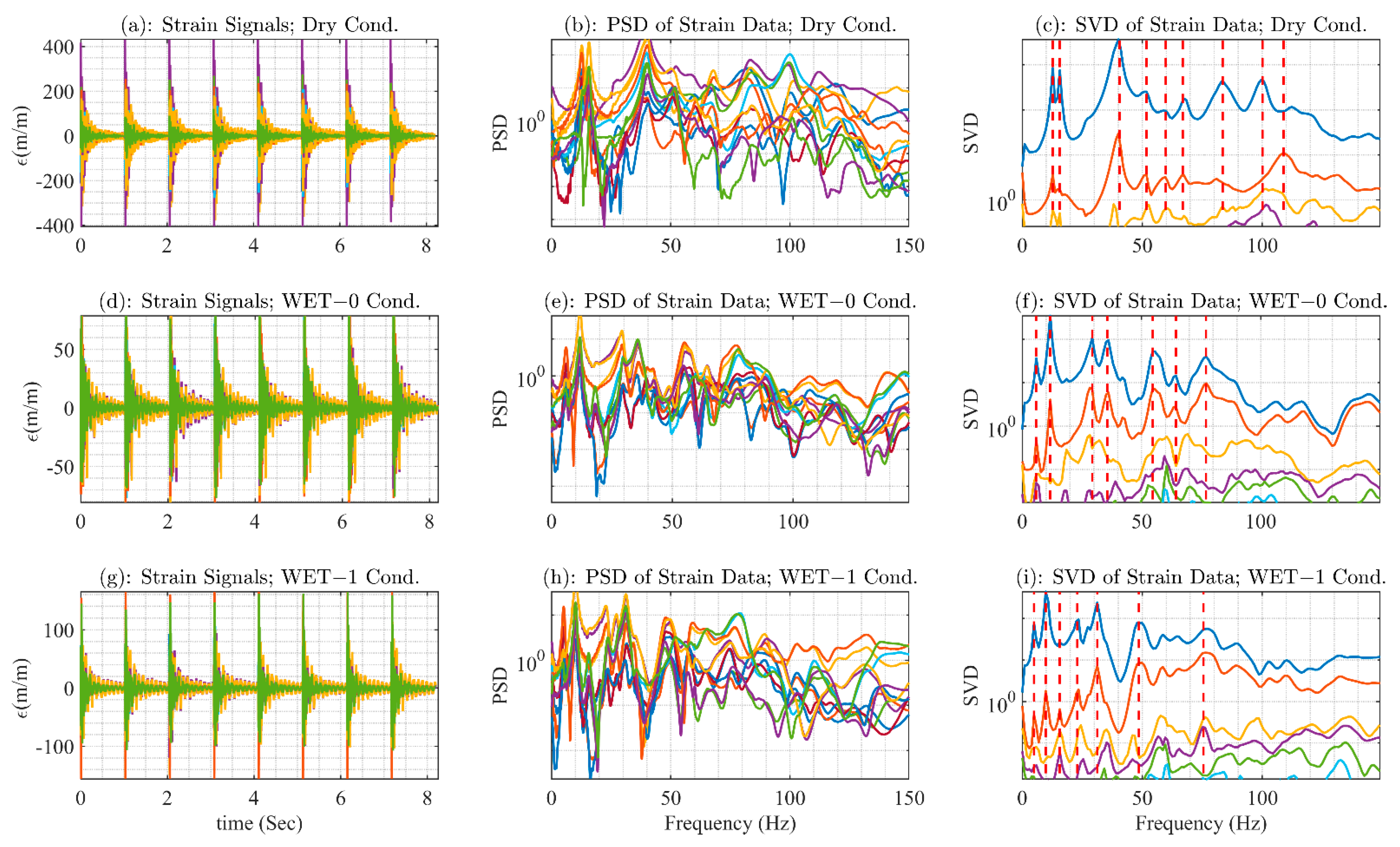
3.5. Experimental Modal Parameter Extraction
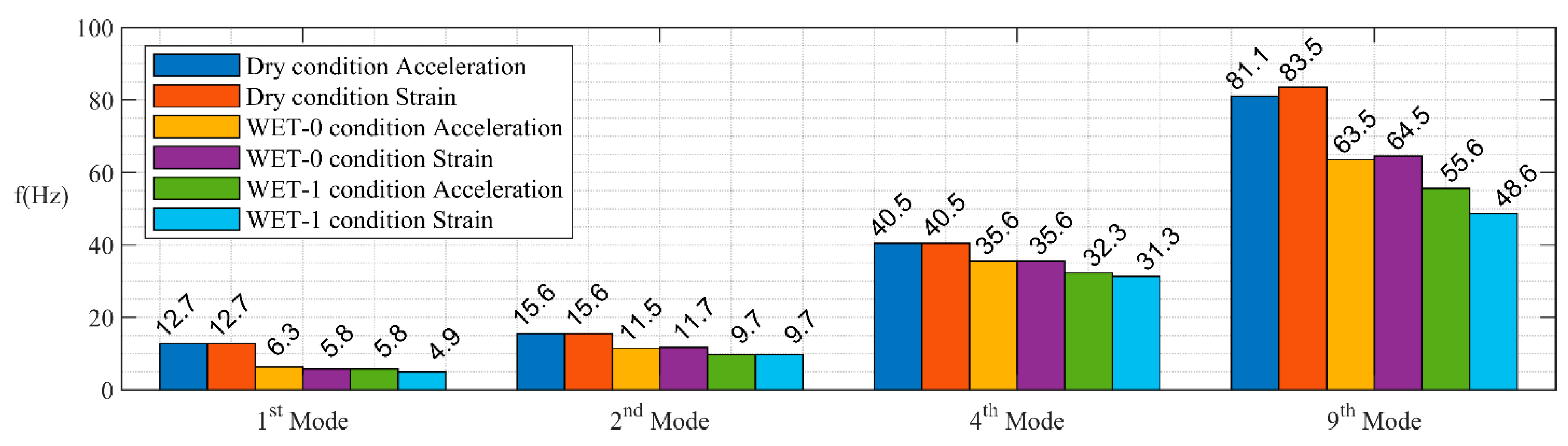
4. Quantification of HAM by Modal Effective Mass
5. Discussion and Results
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Deng, L.; Wang, W.; Yu, Y. State-of-the-art review on the causes and mechanisms of bridge collapse. J. Perform. Constr. Facil. 2016, 30, 04015005. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Limongelli, M.P.; Ademovic, N.; Anžlin, A.; Gavin, K.; Zanini, M. Structural health monitoring for performance assessment of bridges under flooding and seismic actions. Struct. Eng. Int. 2018, 28, 296–307. [Google Scholar] [CrossRef] [Green Version]
- Wardhana, K.; Hadipriono, F.C. Analysis of recent bridge failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef] [Green Version]
- Robertson, I.N.; Riggs, H.R.; Yim, S.C.; Young, Y.L. Lessons from Hurricane Katrina storm surge on bridges and buildings. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 463–483. [Google Scholar] [CrossRef]
- Karimpour, A.; Rahmatalla, S.; Markfort, C. Identification of damage parameters during flood events applicable to multi-span bridges. J. Civ. Struct. Health Monit. 2020, 10, 973–985. [Google Scholar] [CrossRef]
- Qu, K.; Sun, W.Y.; Kraatz, S.; Deng, B.; Jiang, C.B. Effects of floating breakwater on hydrodynamic load of low-lying bridge deck under impact of cnoidal wave. Ocean Eng. 2020, 203, 107217. [Google Scholar] [CrossRef]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami loads on a representative coastal bridge deck: Experimental study and validation of design equations. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Yang, W.; Lai, W.; Zhu, Q.; Zhang, C.; Li, F. Study on generation mechanism of vertical force peak values on T-girder attacked by tsunami bore. Ocean Eng. 2020, 196, 106782. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Dai, S.S.; Day, A.H.; Chan, E.S. Wave-in-deck experiments with focused waves into a solid deck. J. Fluids Struct. 2020, 98, 103139. [Google Scholar] [CrossRef]
- Kulicki, J.M.; Mertz, D.R. Guide Specifications for Bridges Vulnerable to Coastal Storms; AASHTO: Washington, DC, USA, 2008. [Google Scholar]
- Patel, M.H. Dynamics of Offshore Structures; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Newman, J.N. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 2018; p. 448. [Google Scholar]
- Escaler, X.; De La Torre, O.; Goggins, J. Experimental and numerical analysis of directional added mass effects in partially liquid-filled horizontal pipes. J. Fluids Struct. 2017, 69, 252–264. [Google Scholar] [CrossRef]
- Deng, Y.; Guo, Q.; Shah, Y.I.; Xu, L. Study on modal dynamic response and hydrodynamic added mass of water-surrounded hollow bridge pier with pile foundation. Adv. Civ. Eng. 2019, 2019, 1562753. [Google Scholar] [CrossRef] [Green Version]
- Askari, E.; Jeong, K.H.; Ahn, K.H.; Amabili, M. A mathematical approach to study fluid-coupled vibration of eccentric annular plates. J. Fluids Struct. 2020, 98, 103129. [Google Scholar] [CrossRef]
- Sharma, N.; Mahapatra, T.R.; Panda, S.K.; Mazumdar, A. Acoustic radiation characteristics of un-baffled laminated composite conical shell panels. Mater. Today Proc. 2018, 5, 24387–24396. [Google Scholar] [CrossRef]
- Rawat, A.; Mittal, V.; Chakraborty, T.; Matsagar, V. Earthquake induced sloshing and hydrodynamic pressures in rigid liquid storage tanks analyzed by coupled acoustic-structural and Euler-Lagrange methods. Thin-Walled Struct. 2019, 134, 333–346. [Google Scholar] [CrossRef]
- Sepehrirahnama, S.; Xu, D.; Ong, E.T.; Lee, H.P.; Lim, K.M. Fluid–structure interaction effects on free vibration of containerships. J. Offshore Mech. Arct. Eng. 2019, 141, 061603. [Google Scholar] [CrossRef]
- Motley, M.R.; Kramer, M.R.; Young, Y.L. Free surface and solid boundary effects on the free vibration of cantilevered composite plates. Compos. Struct. 2013, 96, 365–375. [Google Scholar] [CrossRef]
- Kramer, M.R.; Liu, Z.; Young, Y.L. Free vibration of cantilevered composite plates in air and in water. Compos. Struct. 2013, 95, 254–263. [Google Scholar] [CrossRef]
- Harwood, C.; Stankovich, A.; Young, Y.L.; Ceccio, S. Combined experimental and numerical study of the free vibration of surface-piercing struts. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- Rawat, A.; Matsagar, V.A.; Nagpal, A.K. Numerical study of base-isolated cylindrical liquid storage tanks using coupled acoustic-structural approach. Soil Dyn. Earthq. Eng. 2019, 119, 196–219. [Google Scholar] [CrossRef]
- Liao, Y.; Garg, N.; Martins, J.R.; Young, Y.L. Viscous fluid–structure interaction response of composite hydrofoils. Compos. Struct. 2019, 212, 571–585. [Google Scholar] [CrossRef]
- Zeng, Y.S.; Yao, Z.F.; Zhou, P.J.; Wang, F.J.; Hong, Y.P. Numerical investigation into the effect of the trailing edge shape on added mass and hydrodynamic damping for a hydrofoil. J. Fluids Struct. 2019, 88, 167–184. [Google Scholar] [CrossRef]
- Eslaminejad, A.; Ziejewski, M.; Karami, G. An experimental–numerical modal analysis for the study of shell-fluid interactions in a clamped hemispherical shell. Appl. Acoust. 2019, 152, 110–117. [Google Scholar] [CrossRef]
- Deng, Y.; Guo, Q.; Xu, L. Experimental and numerical study on modal dynamic response of water-surrounded slender bridge pier with pile foundation. Shock Vib. 2017, 2017, 4769637. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, L.; Escaler, X.; Wang, Z.; Luo, Y.; De La Torre, O. Numerical simulation of added mass effects on a hydrofoil in cavitating flow using acoustic fluid–structure interaction. J. Fluids Eng. 2017, 139, 041301. [Google Scholar] [CrossRef]
- Harwood, C.M.; Felli, M.; Falchi, M.; Garg, N.; Ceccio, S.L.; Young, Y.L. The hydroelastic response of a surface-piercing hydrofoil in multiphase flows. Part 2. Modal parameters and generalized fluid forces. J. Fluid Mech. 2020, 884, A3. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, K.; Qin, S. An efficient numerical model for hydrodynamic added mass of immersed column with arbitrary cross-section. Ocean Eng. 2019, 187, 106192. [Google Scholar] [CrossRef]
- Li, Y.; Di, Q.; Gong, Y. Equivalent mechanical models of sloshing fluid in arbitrary-section aqueducts. Earthq. Eng. Struct. Dyn. 2012, 41, 1069–1087. [Google Scholar] [CrossRef]
- Roh, H.; Lee, H.; Lee, J.S. New lumped-mass-stick model based on modal characteristics of structures: Development and application to a nuclear containment building. Earthq. Eng. Eng. Vib. 2013, 12, 307–317. [Google Scholar] [CrossRef]
- Jia, J. Tank liquid impact. In Modern Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Rajbamshi, S.; Guo, Q.; Zhan, M. Model updating of fluid-structure interaction effects on piping system. In Dynamic Substructures, Volume 4; Conference Proceedings of the Society for Experimental Mechanics Series; Linderholt, A., Allen, M., Mayes, R., Rixen, D., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Carlsson, H. Finite Element Analysis of Structure-Acoustic Systems: Formulations and Solution Strategies. Ph.D. Thesis, Lund University, Lund, Sweden, 1992. [Google Scholar]
- Huang, H.; Zou, M.S.; Jiang, L.W. Study on calculation methods for acoustic radiation of axisymmetric structures in finite water depth. J. Fluids Struct. 2020, 98, 103115. [Google Scholar] [CrossRef]
- Ergin, A.; Temarel, P. Free vibration of a partially liquid-filled and submerged, horizontal cylindrical shell. J. Sound Vib. 2002, 254, 951–965. [Google Scholar] [CrossRef]
- Ergin, A.; Uğurlu, B. Linear vibration analysis of cantilever plates partially submerged in fluid. J. Fluids Struct. 2003, 17, 927–939. [Google Scholar] [CrossRef]
- Kvåle, K.A.; Sigbjörnsson, R.; Øiseth, O. Modelling the stochastic dynamic behaviour of a pontoon bridge: A case study. Comput. Struct. 2016, 165, 123–135. [Google Scholar] [CrossRef]
- Petersen, Ø.W.; Øiseth, O. Sensitivity-based finite element model updating of a pontoon bridge. Eng. Struct. 2017, 150, 573–584. [Google Scholar] [CrossRef] [Green Version]
- Yoon, G.H.; Jensen, J.S.; Sigmund, O. Topology optimization of acoustic–structure interaction problems using a mixed finite element formulation. Int. J. Numer. Methods Eng. 2007, 70, 1049–1075. [Google Scholar] [CrossRef]
- Bouaanani, N.; Lu, F.Y. Assessment of potential-based fluid finite elements for seismic analysis of dam–reservoir systems. Comput. Struct. 2009, 87, 206–224. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Li, D.Y.; Wang, F.; Li, B. Numerical simulation of nonlinear structural responses of an arch dam to an underwater explosion. Eng. Fail. Anal. 2018, 91, 72–91. [Google Scholar] [CrossRef]
- Karimpour, A.; Rahmatalla, S. Extended empirical wavelet transformation: Application to structural updating. J. Sound Vib. 2021, 500, 116026. [Google Scholar] [CrossRef]
- Lei, X.; Wang, Z.; Luo, K. Design, verification, and test of the bridge structure vibration similarity model. J. Aerosp. Eng. 2021, 34, 04020101. [Google Scholar] [CrossRef]
- Castelli, F.; Grasso, S.; Lentini, V.; Sammito, M.S.V. Effects of soil-foundation-interaction on the seismic response of a cooling tower by 3D-FEM analysis. Geosciences 2021, 11, 200. [Google Scholar] [CrossRef]
- Dassault Systèmes. ABAQUS/Analysis User’s Guide; Dassault: Waltham, MA, USA, 2016. [Google Scholar]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef] [Green Version]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Amador, S.; Ørum, M.; Friis, T.; Brincker, R. Application of frequency domain decomposition identification technique to half spectral densities. In Topics in Modal Analysis & Testing, Volume 9; Conference Proceedings of the Society for Experimental Mechanics Series; Mains, M., Dilworth, B., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Araújo, I.G.; Laier, J.E. Operational modal analysis using SVD of power spectral density transmissibility matrices. Mech. Syst. Signal Process. 2014, 46, 129–145. [Google Scholar] [CrossRef]

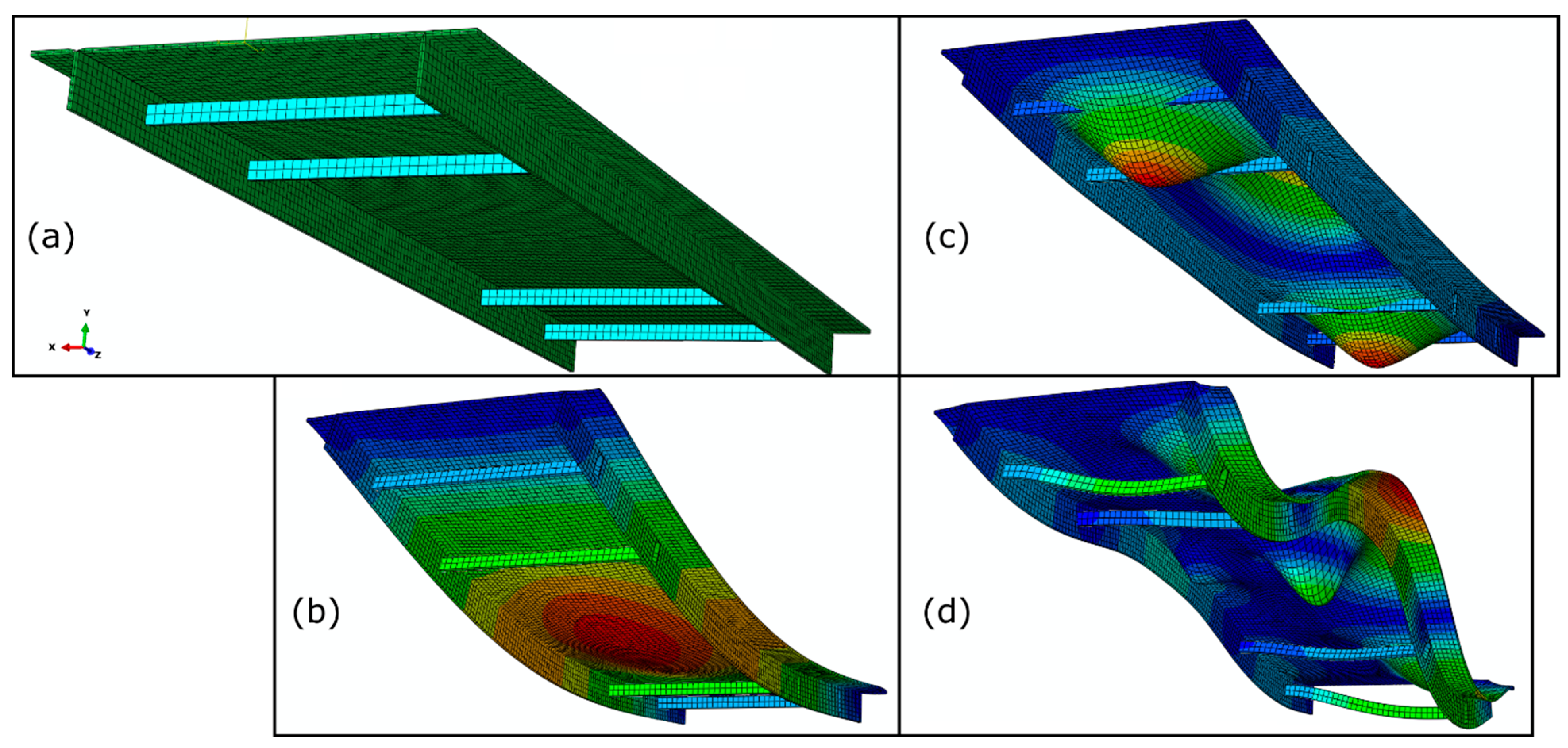
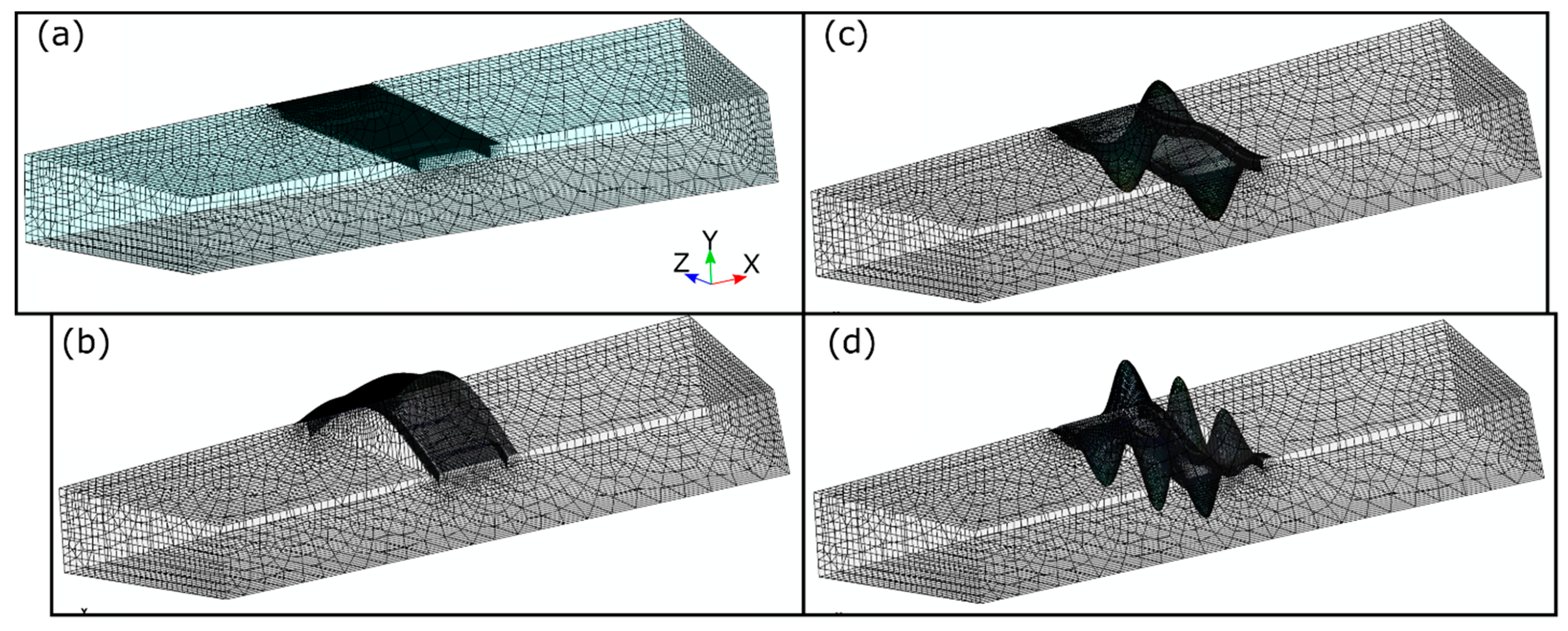

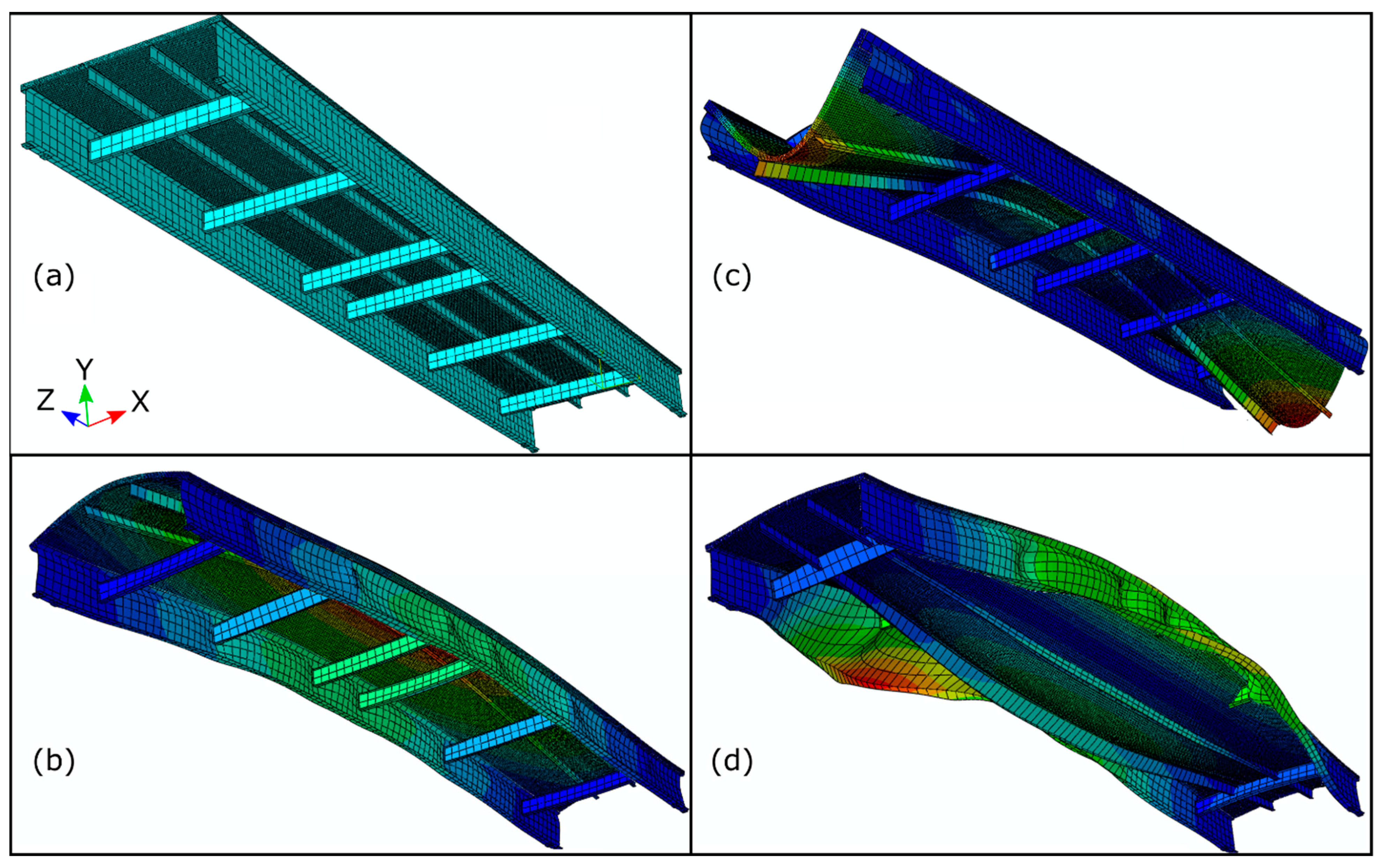
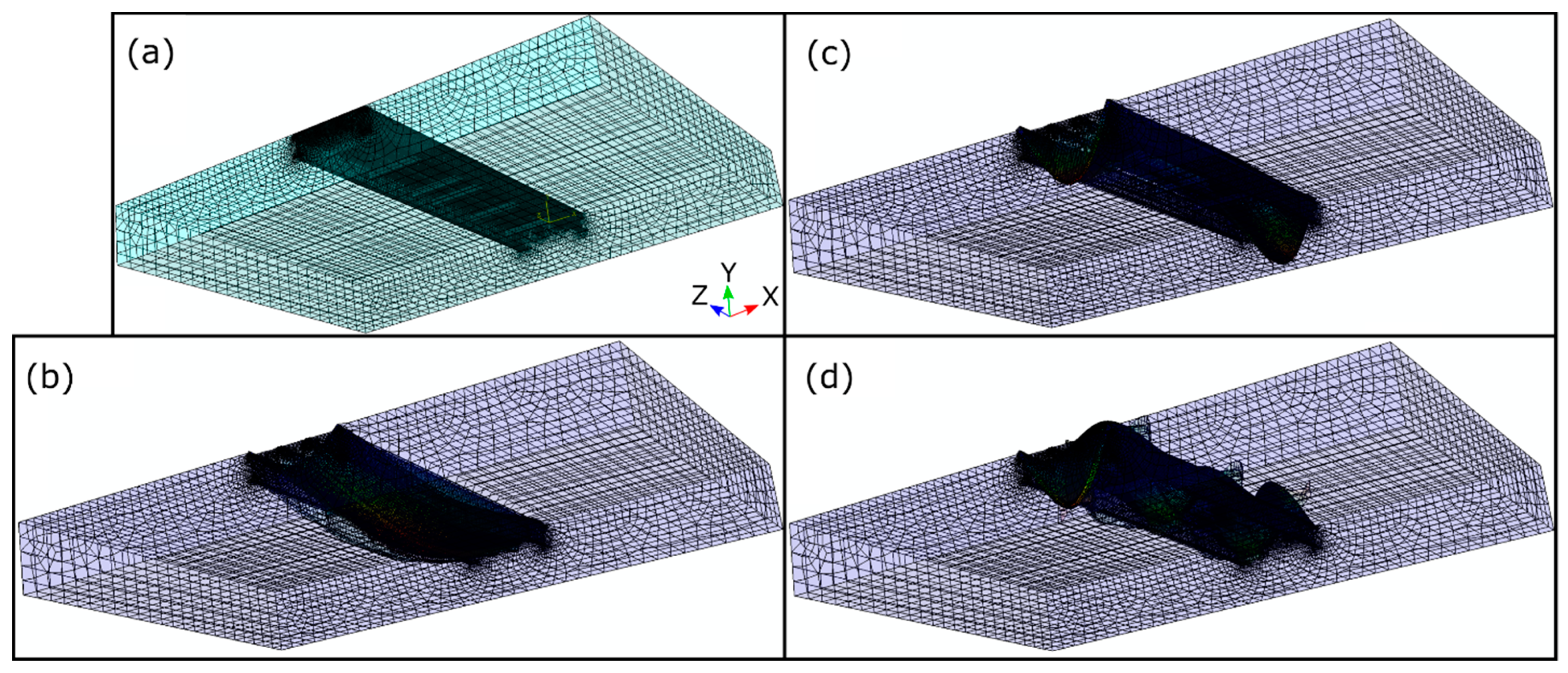

| Characteristic | Nominal Values | |||||
|---|---|---|---|---|---|---|
| Material | Air | Water | Steel | Lexan | Aluminum | Concrete |
| 1.21 | 998 | 7830 | 1060 | 2700 | 2300 | |
| Poisson’s ratio | - | - | 0.3 | 0.38 | 0.33 | 0.2 |
| - | - | 193 | 2.32 | 70 | 22 | |
| 1.39 × 10−4 | 2.19 | 160 | 5.8 | 107.8 | 31.5 | |
| 340 | 1481.3 | 4520 | 2350 | 6320 | 3700 | |
| Dry Condition | Semi-Inundation | Full Inundation | ||||||
|---|---|---|---|---|---|---|---|---|
| Dominant modes | NFs (Hz) | NFs (Hz) | HAM (kg) | NFs (Hz) | HAM (kg) | |||
| 1st mode | 12.43 (12.7) | 4.1247 (81%) | 5.9 (6.3) | 52.5 | 14.2 (+280%) | 5.1 (5.8) | 59 | 20.3 (+403%) |
| 4th mode | 38.91 (40.5) | 0.29 (5.7%) | 32.7 (35.6) | 15.9 | 0.12 (+2.3%) | 29.7 (32.3) | 24 | 0.2 (+4.1%) |
| 17th mode | 165.51 | 0.19 (3.7%) | 103.91 | 37.2 | 0.29 (+5.7%) | 85.1 | 49 | 0.52 (+10%) |
| Dry Condition | Semi-Inundation | Full Inundation | ||||||
|---|---|---|---|---|---|---|---|---|
| Dominant modes | NFs (Hz) | (Metric ton) | NFs (Hz) | HAM (metric ton) | NFs (Hz) | HAM (metric ton) | ||
| 1st mode | 2.57 | 410 (72%) | 1.03 | 60 | 2142 (+375%) | 0.85 | 67 | 3338 (+585%) |
| 4th mode | 3.52 | 34.8 (6.1%) | 1.64 | 53.4 | 125 (+34) | 1.16 | 67 | 285 (+50%) |
| 9th mode | 7.15 | 56 (9.8%) | 4.38 | 38.7 | 93 (+16) | 3.34 | 53 | 200 (+35%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimpour, A.; Rahmatalla, S.; Harwood, C. Effect of Directional Added Mass on Highway Bridge Response during Flood Events. Infrastructures 2022, 7, 42. https://doi.org/10.3390/infrastructures7030042
Karimpour A, Rahmatalla S, Harwood C. Effect of Directional Added Mass on Highway Bridge Response during Flood Events. Infrastructures. 2022; 7(3):42. https://doi.org/10.3390/infrastructures7030042
Chicago/Turabian StyleKarimpour, Ali, Salam Rahmatalla, and Casey Harwood. 2022. "Effect of Directional Added Mass on Highway Bridge Response during Flood Events" Infrastructures 7, no. 3: 42. https://doi.org/10.3390/infrastructures7030042
APA StyleKarimpour, A., Rahmatalla, S., & Harwood, C. (2022). Effect of Directional Added Mass on Highway Bridge Response during Flood Events. Infrastructures, 7(3), 42. https://doi.org/10.3390/infrastructures7030042






