Reliability Analysis of Gravity Retaining Wall Using Hybrid ANFIS
Abstract
:1. Introduction
2. The Proposed AI-Based Hybridized Method
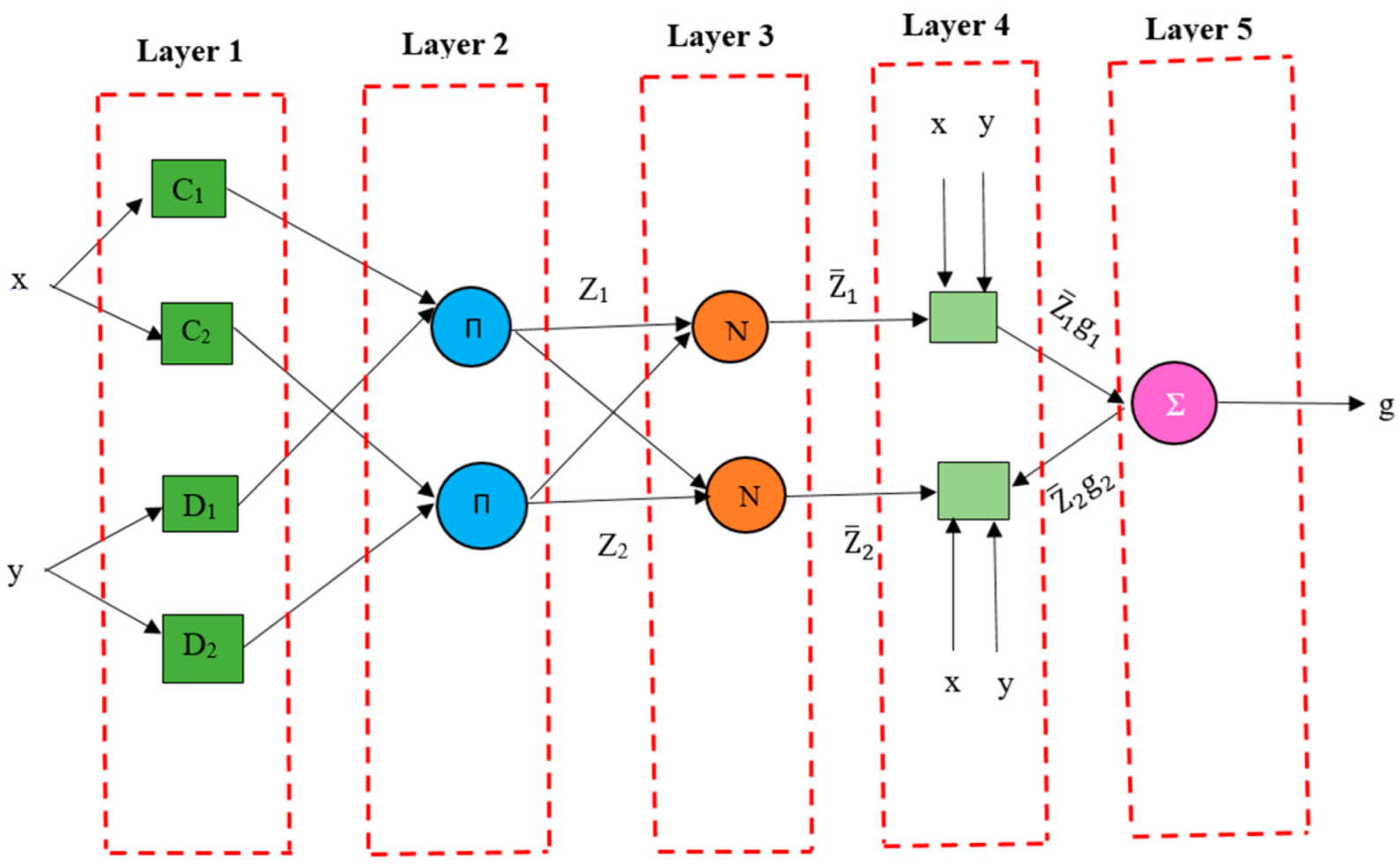
2.1. Adaptive Neuro Fuzzy Inference System (ANFIS)
2.2. Metaheuristic Optimization Algorithm
2.2.1. Particle Swarm Optimization (PSO)
2.2.2. Genetic Algorithm (GA)
2.2.3. Firefly Algorithm (FFA)
2.2.4. Grey Wolf Optimization (GWO)
2.3. Hybrid ANFIS Models
3. Practical Applications to the Gravity Retaining Wall
4. Statistical Performance Parameters
5. Methodology Flowchart
6. Results and Analysis
6.1. Prediction Command
6.2. Rank Analysis
6.3. Reliability Analysis
6.4. Regression Curve
6.5. Williams Plot
6.6. Accuracy and Error Matrix
6.7. Gini Index (GI)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Low, B.K.; Tang, W.H. Efficient Reliability Evaluation Using Spreadsheet. J. Eng. Mech. 1997, 123, 749–752. [Google Scholar] [CrossRef]
- Chan, C.L.; Low, B.K. Practical second-order reliability analysis applied to foundation engineering. Int. J. Numer. Anal. Methods Géoméch. 2011, 36, 1387–1409. [Google Scholar] [CrossRef]
- Cushing, A.G.; Whitman, J.L.; Szwed, A.; Nowak, A.S. Reliability analysis of anchored and cantilevered flexible retaining structures. In Limit State Design in Geotechnical Engineering Practice: (With CD-ROM); World Scientific: Singapore, 2003; pp. 1–38. [Google Scholar] [CrossRef]
- Low, B.; Zhang, J.; Tang, W.H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope. Comput. Geotech. 2011, 38, 196–204. [Google Scholar] [CrossRef]
- GuhaRay, A.; Mondal, S.; Mohiuddin, H.H. Reliability Analysis of Retaining Walls Subjected to Blast Loading by Finite Element Approach. J. Inst. Eng. India Ser. A 2018, 99, 95–102. [Google Scholar] [CrossRef]
- Alghaffar, M.; Wellington, C. Reliability analysis of retaining walls designed to British and European standards. Struct. Infrastruct. Eng. 2005, 1, 271–284. [Google Scholar] [CrossRef]
- Kumar, A.; Roy, P. Reliability analysis of retaining wall using imprecise probability. In Proceedings of the 12th International Conference on Structural Safety and Reliability, Vienna, Austria, 6–10 August 2017; pp. 288–296. [Google Scholar]
- Chouksey, S.K.; Fale, A. Reliability analysis of counterfort retaining wall. Int. J. Civ. Eng. Technol. 2017, 8, 1058–1073. [Google Scholar]
- Cherubini, C. Probabilistic approach to the design of anchored sheet pile walls. Comput. Geotech. 2000, 26, 309–330. [Google Scholar] [CrossRef]
- Yang, Z.; Ching, J. A novel simplified geotechnical reliability analysis method. Appl. Math. Model. 2019, 74, 337–349. [Google Scholar] [CrossRef]
- Menon, D.; Mangalathu, S. Reliability analysis and design of cantilever RC retaining walls against sliding failure. Int. J. Geotech. Eng. 2011, 5, 131–141. [Google Scholar]
- Wang, H.; Chen, H.; Wang, Y.; Han, L.; Li, H. Reliability analysis for stability of the gravity retaining wall under mountain torrent. Syst. Sci. Control Eng. 2020, 8, 434–440. [Google Scholar] [CrossRef]
- Xiao, Z.-Q.; Huang, J.; Wang, Y.-J.; Xu, C.-Y.; Xia, H. Random Reliability Analysis of Gravity Retaining Wall Structural System. In Advances in Engineering Research, Proceedings of the 2014 International Conference on Mechanics and Civil Engineering (ICMCE-14), Wuhan, Chian, 13–14 December 2014; Atlantis Press: Amsterdam, The Netherlands, 2014; pp. 199–204. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.B.; Sun, Z.B.; Zhu, C.Q. Reliability analysis of retaining walls with multiple failure modes. J. Cent. South Univ. 2013, 20, 2879–2886. [Google Scholar] [CrossRef]
- Babu, G.L.S.; Basha, M. Optimum design of cantilever sheet pile walls in sandy soils using inverse reliability approach. Comput. Geotech. 2008, 35, 134–143. [Google Scholar] [CrossRef]
- Low, B.K. Reliability-based design applied to retaining walls. Geotechnique 2005, 55, 63–75. [Google Scholar] [CrossRef]
- Sun, J.; Yuefei, H. Modeling the simultaneous effects of particle size and porosity in simulating geo-materials. Materials 2022, 15, 1576. [Google Scholar] [CrossRef] [PubMed]
- Sun, J. Hard particle force in a soft fracture. Sci. Rep. 2019, 9, 3065. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y. An ensemble method to improve prediction of earthquake-induced soil liquefaction: A multi-dataset study. Neural Comput. Appl. 2020, 33, 1533–1546. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Toufigh, M.M.; Toufigh, V. Application of improved ANFIS approaches to estimate bearing capacity of piles. Soft Comput. 2018, 23, 9537–9549. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A. Multivariate adaptive regression splines for analysis of geotechnical engineering systems. Comput. Geotech. 2012, 48, 82–95. [Google Scholar] [CrossRef]
- Mishra, P.; Samui, P.; Mahmoudi, E. Probabilistic Design of Retaining Wall Using Machine Learning Methods. Appl. Sci. 2021, 11, 5411. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Goh, A.T. Multivariate adaptive regression splines for inverse analysis of soil and wall properties in braced excavation. Tunn. Undergr. Space Technol. 2017, 64, 24–33. [Google Scholar] [CrossRef]
- Xiang, Y.; Goh, A.T.C.; Zhang, W.; Runhong, Z. A multivariate adaptive regression splines model for estimation of maximum wall deflections induced by braced excavation in clays. Geomech. Eng. 2018, 14, 315–324. [Google Scholar]
- Zhang, W.; Zhang, R.; Goh, A.T.C. Multivariate Adaptive Regression Splines Approach to Estimate Lateral Wall Deflection Profiles Caused by Braced Excavations in Clays. Geotech. Geol. Eng. 2017, 36, 1349–1363. [Google Scholar] [CrossRef]
- Mishra, P.; Samui, P. Reliability Analysis of Retaining Wall Using Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS). In Proceedings of the Indian Geotechnical Conference 2019; Springer: Singapore, 2021; pp. 543–557. [Google Scholar] [CrossRef]
- Ghani, S.; Kumari, S.; Bardhan, A. A novel liquefaction study for fine-grained soil using PCA-based hybrid soft computing models. Indian Acad. Sci. 2021, 46, 113. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Gu, X.; Liu, H.; Mei, G.; Zhang, W. Probabilistic stability analysis of earth dam slope under transient seepage using multivariate adaptive regression splines. Bull. Eng. Geol. Environ. 2020, 79, 2763–2775. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Wu, C.; Li, Y.; Liu, Z.; Liu, H. Soft computing approach for prediction of surface settlement induced by earth pressure balance shield tunneling. Undergr. Space 2020, 6, 353–363. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Tang, L.; Zhang, W.; Lacasse, S.; Liu, H.; Gao, L. Efficient reliability analysis of earth dam slope stability using extreme gradient boosting method. Acta Geotech. 2020, 15, 3135–3150. [Google Scholar] [CrossRef]
- Wu, C.; Hong, L.; Wang, L.; Zhang, R.; Pijush, S.; Zhang, W. Prediction of wall deflection induced by braced excavation in spatially variable soils via convolutional neural network. Gondwana Res. 2022, in press. [Google Scholar] [CrossRef]
- Yong, W.; Zhang, W.; Nguyen, H.; Bui, X.-N.; Choi, Y.; Nguyen-Thoi, T.; Zhou, J.; Tran, T.T. Analysis and prediction of diaphragm wall deflection induced by deep braced excavations using finite element method and artificial neural network optimized by metaheuristic algorithms. Reliab. Eng. Syst. Saf. 2022, 221, 108335. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Derivation of fuzzy control rules from human operator’s control actions. IFAC Proc. Vol. 1983, 16, 55–60. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. 2013, 1, 36–50. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Zhou, G.M.; Li, Y.; Zhang, F. Analysis of Reliability Calculation and System Analysis of Gravity Retaining Walls. Appl. Mech. Mater. 2014, 556–562, 862–866. [Google Scholar] [CrossRef]











| Parameters | Cohesion (c) | Unit Weight of Soil (ϒ) | Angle of Shearing Resistance (φ) |
|---|---|---|---|
| Mean | 11 kN/m2 | 16 kN/m3 | 290 |
| Coefficient of variation (%) | 20 | 6 | 12 |
| Standard deviation | 2.2 | 0.96 | 3.48 |
| Minimum | 5.64 kN/m2 | 13.49 kN/m3 | 21.140 |
| Maximum | 16.93 kN/m2 | 17.84 kN/m3 | 37.520 |
| Median | 11.53 | 15.98 | 28.72 |
| Range | 11.29 | 4.34 | 16.39 |
| Standard Error | 0.22 | 0.096 | 0.35 |
| Sample Variance | 5.85 | 0.96 | 11.49 |
| Kurtosis | −0.138 | −0.455 | −0.105 |
| Skewness | −0.097 | −0.019 | 0.286 |
| Parameters | Ideal Value | ANFIS-GA (Training) | ANFIS-PSO (Training) | ANFIS-FFA (Training) | ANFIS-GWO (Training) |
|---|---|---|---|---|---|
| R2 | 1 | 0.984 | 0.997 | 0.995 | 0.897 |
| AdjR2 | 1 | 0.983 | 0.996 | 0.995 | 0.893 |
| RMSE | 0 | 0.025 | 0.012 | 0.014 | 0.063 |
| VAF | 100 | 98.594 | 99.617 | 99.510 | 89.836 |
| WI | 1 | 0.996 | 0.999 | 0.998 | 0.968 |
| LMI | 1 | 0.882 | 0.939 | 0.933 | 0.724 |
| SI | 0.1 | 0.096 | 0.047 | 0.054 | 0.244 |
| a-20 Index | 1 | 0.841 | 0.886 | 0.913 | 0.786 |
| PI | 2 | 1.944 | 1.981 | 1.976 | 1.728 |
| KGE | 1 | 0.936 | 0.994 | 0.922 | 0.762 |
| NMBE | 0 | 3.347 | 0.144 | 0.590 | 2.4062 |
| MAE | 0 | 0.0182 | 0.009 | 0.011 | 0.042 |
| MBE | 0 | 0.009 | 0.001 | 0.002 | 0.006 |
| Parameters | Ideal Value | ANFIS-GA (Testing) | ANFIS-PSO (Testing) | ANFIS-FFA (Testing) | ANFIS-GWO (Testing) |
|---|---|---|---|---|---|
| R2 | 1 | 0.953 | 0.966 | 0.989 | 0.842 |
| AdjR2 | 1 | 0.948 | 0.963 | 0.988 | 0.824 |
| RMSE | 0 | 0.048 | 0.040 | 0.023 | 0.087 |
| VAF | 100 | 95.351 | 96.655 | 99.005 | 84.190 |
| WI | 1 | 0.987 | 0.991 | 0.997 | 0.945 |
| LMI | 1 | 0.784 | 0.842 | 0.900 | 0.656 |
| SI | 0.1 | 0.201 | 0.169 | 0.095 | 0.368 |
| a-20 Index | 1 | 0.767 | 0.733 | 0.867 | 0.767 |
| PI | 2 | 1.853 | 1.889 | 1.955 | 1.579 |
| KGE | 1 | 0.913 | 0.928 | 0.930 | 0.664 |
| NMBE | 0 | 2.265 | 1.374 | 2.401 | 1.279 |
| MAE | 0 | 0.031 | 0.023 | 0.014 | 0.050 |
| MBE | 0 | 0.005 | 0.003 | 0.006 | 0.003 |
| Hybrid Models | Phase | R2 | RMSE | VAF | WI | LMI | SI | a-20 Index | PI | KGE | NMBE | MAE | MBE | Total Rank | Overall Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANFIS-GA | TR | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 4 | 3 | 4 | 36 | 70 |
| TS | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 2 | 34 | ||
| ANFIS-PSO | TR | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 13 | 37 |
| TS | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | 2 | 2 | 1 | 24 | ||
| ANFIS-FFA | TR | 3 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 3 | 2 | 2 | 2 | 25 | 42 |
| TS | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 3 | 17 | ||
| ANFIS-GWO | TR | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 4 | 3 | 46 | 86 |
| TS | 4 | 4 | 4 | 4 | 4 | 4 | 2 | 4 | 4 | 1 | 4 | 1 | 40 |
| Models | Actual β | Actual Pf | Model’s β | Model’s Pf | Rank |
|---|---|---|---|---|---|
| ANFIS-GA | 1.421 | 0.078 | 1.273 | 0.102 | 3 |
| ANFIS-PSO | 1.324 | 0.092 | 1 | ||
| ANFIS-FFA | 1.320 | 0.093 | 2 | ||
| ANFIS-GWO | 1.256 | 0.105 | 4 |
| Error Measuring Parameters | Ideal Value | ANFIS-GA (TR) | Error (εe) | ANFIS-PSO (TR) | Error (εe) | ANFIS-FFA (TR) | Error (εe) | ANFIS-GWO (TR) | Error (εe) |
|---|---|---|---|---|---|---|---|---|---|
| RMSE | 0 | 0.025 | 2.5% | 0.012 | 1.2% | 0.014 | 1.4% | 0.063 | 6.3% |
| SI | 0.1 | 0.096 | 0.4% | 0.047 | 5.3% | 0.054 | 4.6% | 0.244 | 14.4% |
| NMBE | 0 | 3.347 | 3.4% | 0.144 | 14.4% | 0.590 | 0.6% | 2.4062 | 2.4% |
| MAE | 0 | 0.0182 | 1.8% | 0.009 | 0.9% | 0.011 | 1.1% | 0.042 | 4.2% |
| MBE | 0 | 0.009 | 0.9% | 0.001 | 0.1% | 0.002 | 0.2% | 0.006 | 0.6% |
| Error Measuring Parameters | Ideal Value | ANFIS-GA (TS) | Error (εe) | ANFIS-PSO (TS) | Error (εe) | ANFIS-FFA (TS) | Error (εe) | ANFIS-GWO (TS) | Error (εe) |
|---|---|---|---|---|---|---|---|---|---|
| RMSE | 0 | 0.048 | 4.8% | 0.040 | 4% | 0.023 | 2.3% | 0.087 | 8.7% |
| SI | 0.1 | 0.201 | 10.1% | 0.169 | 6.9% | 0.095 | 0.5% | 0.368 | 26.8% |
| NMBE | 0 | 2.265 | 2.3% | 1.374 | 1.4% | 2.401 | 2.4% | 1.279 | 1.3% |
| MAE | 0 | 0.031 | 3.1% | 0.023 | 2.3% | 0.014 | 1.4% | 0.050 | 5% |
| MBE | 0 | 0.005 | 0.5% | 0.003 | 0.3% | 0.006 | 0.6% | 0.003 | 0.3% |
| Trend Measuring Parameters | Ideal Value | ANFIS-GA (TR) | Error (εt) | ANFIS-PSO (TR) | Error (εt) | ANFIS-FFA (TR) | Error (εt) | ANFIS-GWO (TR) | Error (εt) |
|---|---|---|---|---|---|---|---|---|---|
| R2 | 1 | 0.984 | 1.6% | 0.997 | 0.3% | 0.995 | 0.5% | 0.897 | 10.3% |
| AdjR2 | 1 | 0.983 | 1.7% | 0.996 | 0.4% | 0.995 | 0.5% | 0.893 | 10.7% |
| VAF | 100 | 98.594 | 1.4% | 99.617 | 0.3% | 99.510 | 0.5% | 89.836 | 10.2% |
| WI | 1 | 0.996 | 0.4% | 0.999 | 0.1% | 0.998 | 0.2% | 0.968 | 3.2% |
| LMI | 1 | 0.882 | 11.8% | 0.939 | 6.1% | 0.933 | 6.7% | 0.724 | 27.6% |
| a-20 Index | 1 | 0.841 | 15.9% | 0.886 | 11.4% | 0.913 | 8.7% | 0.786 | 21.4% |
| KGE | 1 | 0.936 | 6.4% | 0.994 | 0.6% | 0.922 | 7.8% | 0.762 | 23.8% |
| PI | 2 | 1.944 | 2.8% | 1.981 | 0.9% | 1.976 | 1.2% | 1.728 | 13.6% |
| Trend Measuring Parameters | Ideal Value | ANFIS-GA (TS) | Error (εt) | ANFIS-PSO (TS) | Error (εt) | ANFIS-FFA (TS) | Error (εt) | ANFIS-GWO (TS) | Error (εt) |
|---|---|---|---|---|---|---|---|---|---|
| R2 | 1 | 0.953 | 4.7% | 0.966 | 3.4% | 0.989 | 1.1% | 0.842 | 15.8% |
| AdjR2 | 1 | 0.948 | 5.2% | 0.963 | 3.7% | 0.988 | 1.2% | 0.824 | 17.6% |
| VAF | 100 | 95.351 | 4.7% | 96.655 | 3.3% | 99.005 | 1.0% | 84.190 | 15.8% |
| WI | 1 | 0.987 | 1.3% | 0.991 | 0.9% | 0.997 | 0.3% | 0.945 | 5.5% |
| LMI | 1 | 0.784 | 21.6% | 0.842 | 15.8% | 0.900 | 10% | 0.656 | 34.4% |
| a-20 Index | 1 | 0.767 | 23.3% | 0.733 | 26.7% | 0.867 | 13.3% | 0.767 | 23.3% |
| KGE | 1 | 0.913 | 8.7% | 0.928 | 7.2% | 0.930 | 7.0% | 0.664 | 33.6% |
| PI | 2 | 1.853 | 7.4% | 1.889 | 5.6% | 1.955 | 2.3% | 1.579 | 21.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mustafa, R.; Samui, P.; Kumari, S. Reliability Analysis of Gravity Retaining Wall Using Hybrid ANFIS. Infrastructures 2022, 7, 121. https://doi.org/10.3390/infrastructures7090121
Mustafa R, Samui P, Kumari S. Reliability Analysis of Gravity Retaining Wall Using Hybrid ANFIS. Infrastructures. 2022; 7(9):121. https://doi.org/10.3390/infrastructures7090121
Chicago/Turabian StyleMustafa, Rashid, Pijush Samui, and Sunita Kumari. 2022. "Reliability Analysis of Gravity Retaining Wall Using Hybrid ANFIS" Infrastructures 7, no. 9: 121. https://doi.org/10.3390/infrastructures7090121
APA StyleMustafa, R., Samui, P., & Kumari, S. (2022). Reliability Analysis of Gravity Retaining Wall Using Hybrid ANFIS. Infrastructures, 7(9), 121. https://doi.org/10.3390/infrastructures7090121






