Predictive Stress Modeling of Resilient Modulus in Sandy Subgrade Soils
Abstract
:1. Introduction
2. Materials and Methods
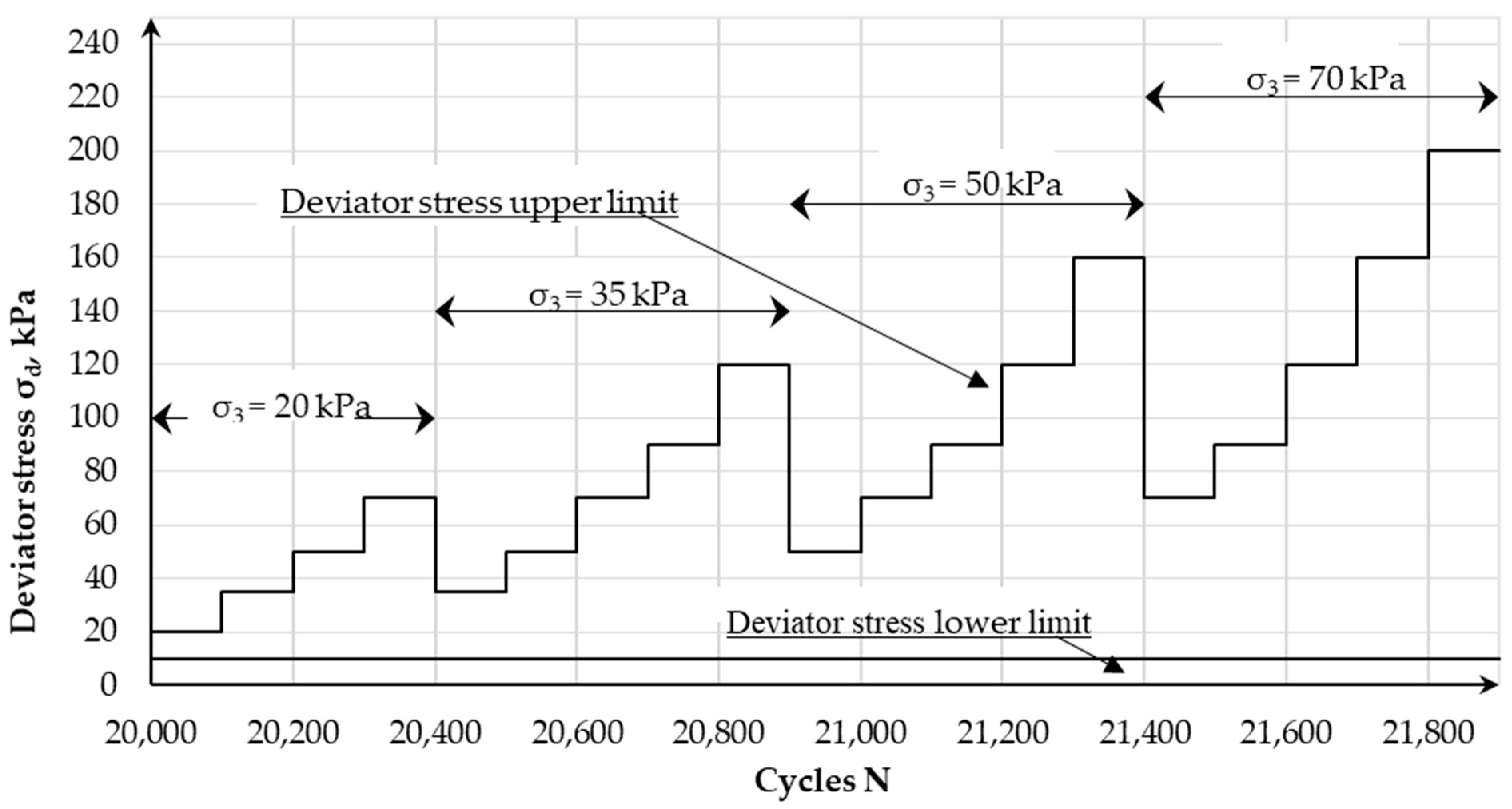
2.1. Test Procedure
2.2. Materials
2.3. Models
3. Results and Discussion
3.1. Test Results
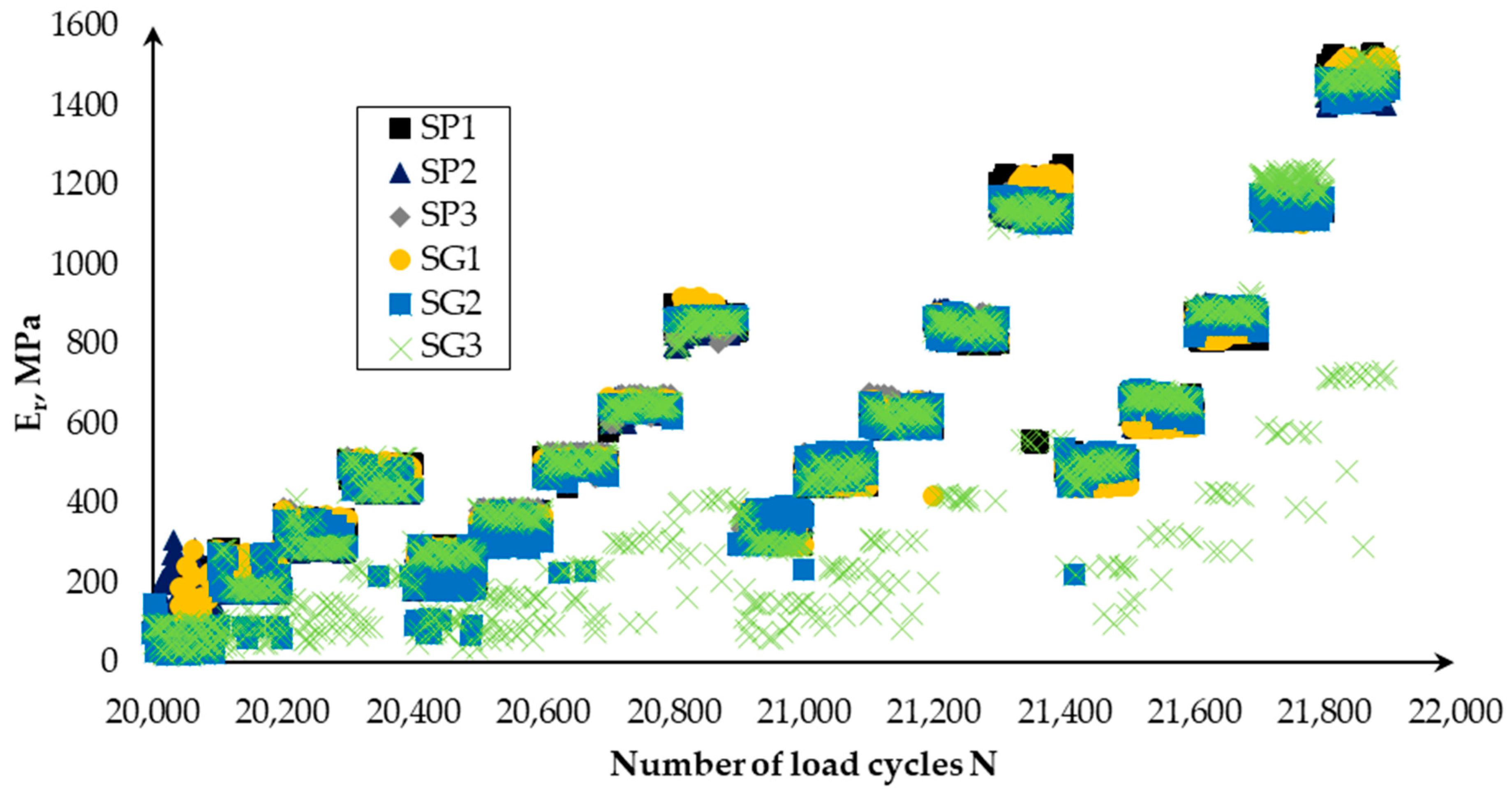
3.2. Modeling Results
3.3. Proposed Model
4. Conclusions
- -
- -
- -
- -
- -
- The Octahedral Shear Stress model, proposed by the authors of the paper, predicts the resilient modulus with a coefficient of determination (R2) ranging from 0.85 to 0.99, using regression coefficients provided in Table 8. The advantage of the model is the use of small-scale data tables, meaning that fixed K1 and K2 regression coefficients can be assigned to a specific specimen type without the need to determine them using specific deviatoric and confining stresses. Additional investigation of the regression coefficient must be performed, separately taking into account different stress states of specimen to avoid overfitting as much as possible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Transportation Officials. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice; AASHTO: Washington, DC, USA, 2008. [Google Scholar]
- EN 13286-7; Unbound and Hydraulically Bound Mixtures–Cyclic Load Triaxial Test for Unbound Mixtures. CEN: Brussels, Belgium, 2004.
- Transportation Officials. AASHTO Guide for Design of Pavement Structures; AASHTO: Washington, DC, USA, 1993. [Google Scholar]
- Kumar, P.; Puppala, A.J.; Tingle, J.S.; Chakraborty, S.; Sarat Chandra Congress, S. Resilient Characteristics of Polymer Emulsion-Treated Sandy Soil. Transp. Res. Rec. 2022, 2676, 526–538. [Google Scholar] [CrossRef]
- Kim, S.S.; Pahno, S.; Durham, S.A.; Yang, J.; Chorzepa, M.G. Prediction of Resilient Modulus from the Laboratory Testing of Sandy Soils; Georgia Department of Transportation, Office of Performance-Based Management and Research: Atlanta, GA, USA, 2019. [Google Scholar]
- Liu, X.; Zhang, X.; Wang, H.; Jiang, B. Laboratory testing and analysis of dynamic and static resilient modulus of subgrade soil under various influencing factors. Constr. Build. Mater. 2019, 195, 178–186. [Google Scholar] [CrossRef]
- Ackah, F.S.; Zhuochen, N.; Huaiping, F. Effect of wetting and drying on the resilient modulus and permanent strain of a sandy clay by RLTT. Int. J. Pavement Res. Technol. 2021, 14, 366–377. [Google Scholar] [CrossRef]
- Yaghoubi, E.; Yaghoubi, M.; Guerrieri, M.; Sudarsanan, N. Improving expansive clay subgrades using recycled glass: Resilient modulus characteristics and pavement performance. Constr. Build. Mater. 2021, 302, 124384. [Google Scholar] [CrossRef]
- Tuan, N.A.; Chieu, P.Q. The Effect of Moisture and Fine Grain Content on the Resilient Modulus of Sandy Clay Embankment Roadbed. Eng. Technol. Appl. Sci. Res. 2021, 11, 7118–7124. [Google Scholar] [CrossRef]
- Behiry, A.E.A.E.M. Fatigue and rutting lives in flexible pavement. Ain Shams Eng. J. 2012, 3, 367–374. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Soból, E.; Bąkowski, J.; Szymański, A. Analysis of the multistage cyclic loading test on resilient modulus value. Ann. Wars. Univ. Life Sci.–SGGW-Land Reclam 2016, 48, 53–65. [Google Scholar] [CrossRef]
- Jin, M.S.; Lee, K.W.; Kovacs, W.D. Seasonal variation of resilient modulus of subgrade soils. J. Transp. Eng. 1994, 120, 603–616. [Google Scholar] [CrossRef]
- Filotenkovas, V.; Vaitkus, A. Influence of the aggregate shape and resistance to fragmentation on unbound base layer resilient modulus. Balt. J. Road Bridge Eng. 2022, 17, 104–119. [Google Scholar] [CrossRef]
- Titi, H.H.; Elias, M.B.; Helwany, S. Determination of Typical Resilient Modulus Values for Selected Soils in Wisconsin; Wisconsin Highway Research Program: Madison, WI, USA, 2006. [Google Scholar]
- Tamošiūnas, T.; Žaržojus, G.; Skuodis, Š. Indirect determination of soil Young’s modulus in Lithuania using cone penetration test data. Balt. J. Road Brodge Eng. 2022, 17, 1–24. [Google Scholar] [CrossRef]
- Fathi, A.; Tirado, C.; Rocha, S.; Mazari, M.; Nazarian, S. A Machine-Learning Approach for Extracting Modulus of Compacted Unbound Aggregate Base and Subgrade Materials Using Intelligent Compaction Technology. Infrastructures 2021, 6, 142. [Google Scholar] [CrossRef]
- Pahno, S.; Yang, J.J.; Kim, S.S. Use of machine learning algorithms to predict subgrade resilient modulus. Infrastructures 2021, 6, 78. [Google Scholar] [CrossRef]
- Skuodis, Š.; Karpis, R.; Zakarka, M.; Gedvilas, M.; Raginis, V.; Orlova, K.; Katauskas, M. Grunto, veikiamo periodinėmis apkrovomis, elgsenos tyrimai. Geol. Geogr. 2018, 4, 159–167. [Google Scholar] [CrossRef]
- LST 1331; Automobilių Kelių Gruntai. Klasifikacija [Soil for roads. Classification]. LSD: Vilnius, Lithuania, 2022.
- Daryati, D.; Widiasanti, I.; Septiandini, E.; Ramadhan, M.A.; Sambowo, K.A.; Purnomo, A. Soil characteristics analysis based on the unified soil classification system. J. Phys. Conf. Ser. 2019, 1402, 022028. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Zeng, L.; Li, J.; Li, F. Rapid estimation of resilient modulus of subgrade soils using performance-related soil properties. Int. J. Pavement Eng. 2021, 22, 732–739. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Liu, W.; Lu, W. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction. Road Mater. Pavement Des. 2021, 22, 703–715. [Google Scholar] [CrossRef]
- Hanandeh, S.; Ardah, A.; Abu-Farsakh, M. Using artificial neural network and genetics algorithm to estimate the resilient modulus for stabilized subgrade and propose new empirical formula. Transp. Geotech. 2020, 24, 100358. [Google Scholar] [CrossRef]
- Hicks, R.G. Factors Influencing the Resilient Properties of Granular Materials; University of California, Berkeley: Berkeley, CA, USA, 1970. [Google Scholar]
- Adomako, S.; Engelsen, C.J.; Thorstensen, R.T.; Barbieri, D.M. Repeated load triaxial testing of recycled excavation materials blended with recycled phyllite materials. Materials 2022, 15, 621. [Google Scholar] [CrossRef]
- Chowdhury, S.R.M. Evaluation of resilient modulus constitutive equations for unbound coarse materials. Constr. Build. Mater. 2021, 296, 123688. [Google Scholar] [CrossRef]
- Rahim, A.M.; George, K.P. Models to estimate subgrade resilient modulus for pavement design. Int. J. Pavement Eng. 2005, 6, 89–96. [Google Scholar] [CrossRef]
- Fedakar, H.I. Developing New Empirical Formulae for the Resilient Modulus of Fine-Grained Subgrade Soils Using a Large Long-Term Pavement Performance Dataset and Artificial Neural Network Approach. Transp. Res. Rec. 2022, 2676, 58–75. [Google Scholar] [CrossRef]
- Uzan, J. Characterization of granular material. Transp. Res. Rec. 1985, 1022, 52–59. [Google Scholar]
- Ni, B.; Hopkins, T.C.; Sun, L.; Beckham, T.L. Modeling the resilient modulus of soils. In Bearing Capacity of Roads, Railways and Airfields; CRC Press: Boca Raton, FL, USA, 2020; pp. 1131–1142. [Google Scholar]
- Yoder, E.J.; Witczak, M.W. Chapter 2: Stresses in flexible pavements. In Principles of Pavement Design; John Wiley and Sons Inc.: New York, NY, USA, 1975; pp. 24–76. [Google Scholar]
- Al-Dulaimi, Y.F.; Awed, A.M.; Gabr, A.R.; El-Badawy, S.M. Predicting Resilient Modulus of Unbound Granular Base/Subbase Material.(Dept. C). MEJ. Mansoura Eng. J. 2022, 47, 1–10. [Google Scholar] [CrossRef]





| Name of Specimen | Cu | Cc | Soil Classification | |
|---|---|---|---|---|
| LST 1331:2022 | USCS | |||
| SP1 | 4.90 | 0.72 | Variously graded sand (SP) | Silty sand (SM) |
| SP2 | 4.74 | 0.75 | Variously graded sand (SP) | Poorly graded sand (SP) |
| SP3 | 4.60 | 0.99 | Variously graded sand (SP) | Silty sand (SM) |
| SG1 | 8.29 | 1.21 | Well-graded sand (SG) | Well-graded sand (SW) |
| SG2 | 17.69 | 1.39 | Well-graded sand (SG) | Well-graded sand (SW) |
| SG3 | 6.23 | 1.07 | Well-graded sand (SG) | Well-graded sand (SW) |
| Start Cycle | No. of Cycles | σd | σ3 | K-θ | Rahim and George | Uzan | Universal Witczak | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K1 | K2 | K1 | K2 | K3 | K1 | K2 | K3 | ||||
| 20,100 | 100 | 20.21 | 20.13 | 0.79 | 1.07 | 0.40 | 0.46 | 1.33 | 0.76 | 0.18 | 0.97 | 1.02 | 0.99 |
| 20,200 | 100 | 34.98 | 20.41 | 0.96 | 1.17 | 0.73 | 0.76 | 2.16 | 0.86 | 0.03 | 1.78 | 0.94 | 1.12 |
| 20,300 | 100 | 49.81 | 21.06 | 1.03 | 1.23 | 1.01 | 1.01 | 3.02 | 1.21 | 0.03 | 2.29 | 1.10 | 1.30 |
| 20,400 | 100 | 69.13 | 22.13 | 1.05 | 1.25 | 1.23 | 1.25 | 3.08 | 1.67 | 0.04 | 2.21 | 1.36 | 1.43 |
| 20,500 | 100 | 35.01 | 35.41 | 0.91 | 1.12 | 0.73 | 0.73 | 1.69 | 1.27 | 0.09 | 1.44 | 1.10 | 1.05 |
| 20,600 | 100 | 49.91 | 35.45 | 0.99 | 1.16 | 0.92 | 0.92 | 1.95 | 1.50 | 0.11 | 1.61 | 1.22 | 1.11 |
| 20,700 | 100 | 69.61 | 35.63 | 1.04 | 1.20 | 1.14 | 1.18 | 2.21 | 1.82 | 0.39 | 1.68 | 1.41 | 1.22 |
| 20,800 | 100 | 89.22 | 35.79 | 1.04 | 1.22 | 1.30 | 1.37 | 2.13 | 1.89 | 0.81 | 1.63 | 1.45 | 1.25 |
| 20,900 | 100 | 116.99 | 38.56 | 1.04 | 1.24 | 1.52 | 1.61 | 1.87 | 1.72 | 1.14 | 1.54 | 1.46 | 1.26 |
| 21,000 | 100 | 49.89 | 50.30 | 0.99 | 1.09 | 0.85 | 0.81 | 1.63 | 1.49 | 0.47 | 1.19 | 1.12 | 1.04 |
| 21,100 | 100 | 69.84 | 50.07 | 1.02 | 1.13 | 1.02 | 1.03 | 1.72 | 1.58 | 0.71 | 1.28 | 1.22 | 1.08 |
| 21,200 | 100 | 89.61 | 49.98 | 1.03 | 1.16 | 1.18 | 1.23 | 1.64 | 1.63 | 0.90 | 1.33 | 1.29 | 1.12 |
| 21,300 | 100 | 118.98 | 50.11 | 1.03 | 1.20 | 1.40 | 1.49 | 1.53 | 1.56 | 1.09 | 1.33 | 1.35 | 1.16 |
| 21,400 | 100 | 155.95 | 53.27 | 1.02 | 1.23 | 1.60 | 1.80 | 1.38 | 1.47 | 1.19 | 1.30 | 1.38 | 1.19 |
| 21,500 | 100 | 70.02 | 69.80 | 1.02 | 1.09 | 0.98 | 0.97 | 1.45 | 1.46 | 0.82 | 1.12 | 1.12 | 1.03 |
| 21,600 | 100 | 89.70 | 70.44 | 1.02 | 1.12 | 1.11 | 1.16 | 1.42 | 1.47 | 0.94 | 1.18 | 1.19 | 1.06 |
| 21,700 | 100 | 119.53 | 69.81 | 1.02 | 1.14 | 1.28 | 1.37 | 1.32 | 1.38 | 1.05 | 1.18 | 1.21 | 1.08 |
| 21,800 | 100 | 158.75 | 69.91 | 1.03 | 1.19 | 1.51 | 1.68 | 1.25 | 1.34 | 1.12 | 1.20 | 1.27 | 1.12 |
| 21,900 | 100 | 196.49 | 71.60 | 1.04 | 1.21 | 1.77 | 1.90 | 1.20 | 1.29 | 1.14 | 1.20 | 1.29 | 1.14 |
| R2 | 0.983835 | 0.984907 | 0.984669 | 0.984817 | |||||||||
| Start Cycle | No. of Cycles | σd | σ3 | K-θ | Rahim and George | Uzan | Universal Witczak | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K1 | K2 | K1 | K2 | K3 | K1 | K2 | K3 | ||||
| 20,100 | 100 | 19.67 | 20.70 | 1.02 | 1.08 | 0.54 | 0.50 | 1.75 | 0.76 | 0.13 | 1.43 | 0.90 | 1.04 |
| 20,200 | 100 | 34.42 | 20.57 | 1.02 | 1.16 | 0.73 | 0.76 | 2.16 | 0.88 | 0.02 | 1.80 | 0.93 | 1.13 |
| 20,300 | 100 | 49.25 | 20.58 | 1.04 | 1.21 | 0.97 | 0.97 | 2.82 | 1.18 | 0.03 | 2.16 | 1.08 | 1.24 |
| 20,400 | 100 | 69.39 | 20.73 | 1.05 | 1.25 | 1.22 | 1.24 | 3.04 | 1.65 | 0.01 | 2.19 | 1.35 | 1.42 |
| 20,500 | 100 | 34.74 | 35.71 | 1.03 | 1.13 | 0.81 | 0.75 | 1.86 | 1.29 | 0.02 | 1.60 | 1.18 | 1.09 |
| 20,600 | 100 | 49.66 | 35.76 | 1.03 | 1.17 | 0.97 | 0.95 | 2.06 | 1.52 | 0.07 | 1.71 | 1.29 | 1.15 |
| 20,700 | 100 | 69.73 | 35.76 | 1.04 | 1.20 | 1.15 | 1.19 | 2.22 | 1.83 | 0.39 | 1.69 | 1.42 | 1.22 |
| 20,800 | 100 | 89.55 | 35.78 | 1.04 | 1.22 | 1.31 | 1.38 | 2.13 | 1.89 | 0.81 | 1.63 | 1.46 | 1.25 |
| 20,900 | 100 | 119.19 | 35.73 | 1.04 | 1.24 | 1.52 | 1.61 | 1.85 | 1.69 | 1.14 | 1.53 | 1.45 | 1.26 |
| 21,000 | 100 | 49.88 | 50.75 | 1.01 | 1.10 | 0.88 | 0.83 | 1.65 | 1.51 | 0.45 | 1.23 | 1.15 | 1.05 |
| 21,100 | 100 | 69.81 | 51.11 | 1.03 | 1.15 | 1.06 | 1.08 | 1.78 | 1.65 | 0.67 | 1.34 | 1.28 | 1.10 |
| 21,200 | 100 | 89.70 | 50.75 | 1.03 | 1.17 | 1.20 | 1.26 | 1.67 | 1.67 | 0.90 | 1.35 | 1.32 | 1.13 |
| 21,300 | 100 | 119.44 | 51.21 | 1.04 | 1.20 | 1.42 | 1.52 | 1.54 | 1.58 | 1.09 | 1.35 | 1.37 | 1.17 |
| 21,400 | 100 | 159.00 | 50.89 | 1.04 | 1.22 | 1.63 | 1.79 | 1.38 | 1.42 | 1.17 | 1.30 | 1.36 | 1.18 |
| 21,500 | 100 | 69.92 | 70.74 | 1.02 | 1.10 | 1.00 | 0.99 | 1.47 | 1.50 | 0.81 | 1.15 | 1.15 | 1.04 |
| 21,600 | 100 | 89.81 | 70.91 | 1.02 | 1.13 | 1.12 | 1.18 | 1.44 | 1.50 | 0.94 | 1.19 | 1.21 | 1.07 |
| 21,700 | 100 | 119.79 | 71.20 | 1.03 | 1.16 | 1.32 | 1.42 | 1.36 | 1.43 | 1.06 | 1.21 | 1.26 | 1.10 |
| 21,800 | 100 | 159.53 | 70.92 | 1.03 | 1.19 | 1.51 | 1.69 | 1.25 | 1.34 | 1.12 | 1.20 | 1.27 | 1.12 |
| 21,900 | 100 | 198.92 | 71.31 | 1.03 | 1.20 | 1.76 | 1.87 | 1.18 | 1.26 | 1.12 | 1.18 | 1.26 | 1.12 |
| R2 | 0.995557 | 0.995565 | 0.995525 | 0.995596 | |||||||||
| Start Cycle | No. of Cycles | σd | σ3 | K-θ | Rahim and George | Uzan | Universal Witczak | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K1 | K2 | K1 | K2 | K3 | K1 | K2 | K3 | ||||
| 20,100 | 100 | 20.06 | 19.92 | 1.00 | 0.98 | 0.38 | 0.39 | 1.40 | 0.89 | 0.28 | 0.84 | 1.04 | 0.99 |
| 20,200 | 100 | 34.74 | 20.06 | 1.03 | 1.14 | 0.71 | 0.73 | 1.96 | 0.91 | 0.00 | 1.67 | 0.95 | 1.10 |
| 20,300 | 100 | 49.84 | 20.28 | 1.04 | 1.21 | 0.97 | 0.97 | 2.74 | 1.16 | 0.00 | 2.13 | 1.08 | 1.23 |
| 20,400 | 100 | 69.53 | 20.20 | 1.05 | 1.24 | 1.21 | 1.22 | 2.98 | 1.61 | 0.02 | 2.14 | 1.33 | 1.39 |
| 20,500 | 100 | 34.91 | 35.68 | 1.03 | 1.13 | 0.81 | 0.76 | 1.85 | 1.28 | 0.02 | 1.60 | 1.18 | 1.09 |
| 20,600 | 100 | 49.83 | 35.74 | 1.03 | 1.17 | 0.97 | 0.96 | 2.07 | 1.52 | 0.06 | 1.71 | 1.29 | 1.15 |
| 20,700 | 100 | 69.60 | 35.68 | 1.04 | 1.20 | 1.15 | 1.19 | 2.22 | 1.83 | 0.38 | 1.69 | 1.42 | 1.22 |
| 20,800 | 100 | 89.55 | 35.68 | 1.04 | 1.22 | 1.31 | 1.38 | 2.13 | 1.89 | 0.81 | 1.63 | 1.46 | 1.25 |
| 20,900 | 100 | 119.55 | 35.56 | 1.04 | 1.24 | 1.53 | 1.61 | 1.86 | 1.70 | 1.14 | 1.54 | 1.46 | 1.26 |
| 21,000 | 100 | 49.88 | 50.90 | 1.02 | 1.10 | 0.89 | 0.83 | 1.66 | 1.52 | 0.44 | 1.24 | 1.16 | 1.05 |
| 21,100 | 100 | 69.86 | 50.88 | 1.03 | 1.14 | 1.05 | 1.07 | 1.77 | 1.64 | 0.68 | 1.33 | 1.27 | 1.10 |
| 21,200 | 100 | 89.70 | 51.16 | 1.03 | 1.17 | 1.21 | 1.28 | 1.68 | 1.69 | 0.89 | 1.37 | 1.33 | 1.14 |
| 21,300 | 100 | 119.74 | 50.79 | 1.04 | 1.20 | 1.41 | 1.51 | 1.53 | 1.57 | 1.09 | 1.34 | 1.36 | 1.16 |
| 21,400 | 100 | 159.51 | 50.80 | 1.04 | 1.22 | 1.63 | 1.79 | 1.38 | 1.42 | 1.17 | 1.30 | 1.36 | 1.18 |
| 21,500 | 100 | 69.95 | 70.69 | 1.02 | 1.10 | 0.99 | 0.99 | 1.47 | 1.50 | 0.81 | 1.15 | 1.15 | 1.04 |
| 21,600 | 100 | 89.92 | 71.23 | 1.02 | 1.13 | 1.13 | 1.19 | 1.44 | 1.50 | 0.94 | 1.20 | 1.22 | 1.07 |
| 21,700 | 100 | 119.84 | 70.90 | 1.03 | 1.16 | 1.31 | 1.41 | 1.36 | 1.42 | 1.06 | 1.21 | 1.25 | 1.09 |
| 21,800 | 100 | 159.55 | 71.21 | 1.03 | 1.19 | 1.52 | 1.69 | 1.25 | 1.34 | 1.12 | 1.21 | 1.27 | 1.12 |
| 21,900 | 100 | 199.62 | 70.94 | 1.03 | 1.21 | 1.76 | 1.88 | 1.18 | 1.26 | 1.12 | 1.18 | 1.26 | 1.12 |
| R2 | 0.997692 | 0.997666 | 0.997671 | 0.997683 | |||||||||
| Start Cycle | No. of Cycles | σd | σ3 | K-θ | Rahim and George | Uzan | Universal Witczak | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K1 | K2 | K1 | K2 | K3 | K1 | K2 | K3 | ||||
| 20,100 | 100 | 20.11 | 20.04 | 0.65 | 1.04 | 0.31 | 0.41 | 1.10 | 0.78 | 0.29 | 0.72 | 1.10 | 0.97 |
| 20,200 | 100 | 34.71 | 20.29 | 0.87 | 1.18 | 0.68 | 0.74 | 2.01 | 0.87 | 0.05 | 1.65 | 0.96 | 1.08 |
| 20,300 | 100 | 50.01 | 20.25 | 0.96 | 1.22 | 0.97 | 0.97 | 2.84 | 1.18 | 0.06 | 2.13 | 1.07 | 1.22 |
| 20,400 | 100 | 69.92 | 20.29 | 1.04 | 1.24 | 1.20 | 1.23 | 3.00 | 1.63 | 0.06 | 2.14 | 1.33 | 1.39 |
| 20,500 | 100 | 35.07 | 35.36 | 3.07 | 1.12 | 0.65 | 0.72 | 1.51 | 1.27 | 0.08 | 1.28 | 1.05 | 1.03 |
| 20,600 | 100 | 50.06 | 35.38 | 0.95 | 1.16 | 0.88 | 0.91 | 1.86 | 1.50 | 0.11 | 1.55 | 1.18 | 1.09 |
| 20,700 | 100 | 70.00 | 35.64 | 1.03 | 1.19 | 1.12 | 1.16 | 2.17 | 1.79 | 0.42 | 1.63 | 1.39 | 1.21 |
| 20,800 | 100 | 89.84 | 35.68 | 1.04 | 1.22 | 1.31 | 1.38 | 2.13 | 1.89 | 0.81 | 1.63 | 1.46 | 1.25 |
| 20,900 | 100 | 119.85 | 35.68 | 1.04 | 1.24 | 1.54 | 1.63 | 1.87 | 1.72 | 1.14 | 1.55 | 1.47 | 1.27 |
| 21,000 | 100 | 50.16 | 50.91 | 0.99 | 1.11 | 0.89 | 0.84 | 1.66 | 1.53 | 0.43 | 1.25 | 1.17 | 1.05 |
| 21,100 | 100 | 70.09 | 50.95 | 1.02 | 1.14 | 1.05 | 1.08 | 1.76 | 1.64 | 0.68 | 1.33 | 1.27 | 1.10 |
| 21,200 | 100 | 89.92 | 50.29 | 1.03 | 1.16 | 1.19 | 1.24 | 1.65 | 1.64 | 0.90 | 1.33 | 1.30 | 1.12 |
| 21,300 | 100 | 119.88 | 50.51 | 1.03 | 1.20 | 1.40 | 1.50 | 1.53 | 1.56 | 1.09 | 1.33 | 1.35 | 1.16 |
| 21,400 | 100 | 159.86 | 50.91 | 1.01 | 1.23 | 1.63 | 1.79 | 1.38 | 1.42 | 1.17 | 1.29 | 1.37 | 1.18 |
| 21,500 | 100 | 70.14 | 70.58 | 0.99 | 1.07 | 0.96 | 0.97 | 1.41 | 1.46 | 0.83 | 1.11 | 1.11 | 1.03 |
| 21,600 | 100 | 90.08 | 71.13 | 1.02 | 1.13 | 1.13 | 1.19 | 1.44 | 1.50 | 0.94 | 1.20 | 1.21 | 1.07 |
| 21,700 | 100 | 119.93 | 70.98 | 9.72 | 1.15 | 1.31 | 1.42 | 1.36 | 1.43 | 1.06 | 1.27 | 1.24 | 1.09 |
| 21,800 | 100 | 160.02 | 70.42 | 1.03 | 1.18 | 1.51 | 1.67 | 1.24 | 1.32 | 1.11 | 1.20 | 1.26 | 1.11 |
| 21,900 | 100 | 199.62 | 70.71 | 1.03 | 1.20 | 1.76 | 1.87 | 1.18 | 1.25 | 1.12 | 1.18 | 1.26 | 1.12 |
| R2 | 0.244736 | 0.991775 | 0.991805 | 0.991622 | |||||||||
| Start Cycle | No. of Cycles | σd | σ3 | K-θ | Rahim and George | Uzan | Universal Witczak | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K1 | K2 | K1 | K2 | K3 | K1 | K2 | K3 | ||||
| 20,100 | 100 | 20.23 | 20.32 | 0.78 | 1.09 | 0.43 | 0.47 | 1.39 | 0.74 | 0.16 | 1.07 | 1.01 | 1.00 |
| 20,200 | 100 | 34.90 | 20.38 | 0.92 | 1.18 | 0.73 | 0.76 | 2.16 | 0.87 | 0.04 | 1.77 | 0.95 | 1.11 |
| 20,300 | 100 | 49.98 | 20.53 | 0.99 | 1.23 | 0.99 | 0.99 | 2.92 | 1.20 | 0.04 | 2.21 | 1.09 | 1.26 |
| 20,400 | 100 | 69.82 | 21.03 | 1.05 | 1.26 | 1.25 | 1.27 | 3.12 | 1.71 | 0.01 | 2.24 | 1.38 | 1.45 |
| 20,500 | 100 | 35.17 | 35.50 | 3.34 | 1.13 | 0.74 | 0.74 | 1.70 | 1.28 | 0.06 | 1.45 | 1.09 | 1.05 |
| 20,600 | 100 | 50.01 | 35.51 | 0.98 | 1.17 | 0.94 | 0.93 | 2.00 | 1.50 | 0.10 | 1.64 | 1.23 | 1.12 |
| 20,700 | 100 | 69.90 | 35.69 | 1.04 | 1.20 | 1.15 | 1.18 | 2.22 | 1.83 | 0.39 | 1.68 | 1.42 | 1.22 |
| 20,800 | 100 | 89.82 | 35.74 | 1.04 | 1.22 | 1.31 | 1.39 | 2.13 | 1.90 | 0.81 | 1.64 | 1.46 | 1.25 |
| 20,900 | 100 | 119.51 | 36.04 | 1.04 | 1.24 | 1.54 | 1.63 | 1.87 | 1.72 | 1.14 | 1.55 | 1.48 | 1.27 |
| 21,000 | 100 | 50.02 | 50.27 | 0.95 | 1.10 | 0.84 | 0.81 | 1.61 | 1.48 | 0.49 | 1.17 | 1.11 | 1.03 |
| 21,100 | 100 | 69.88 | 50.44 | 1.02 | 1.14 | 1.03 | 1.05 | 1.75 | 1.61 | 0.70 | 1.30 | 1.24 | 1.09 |
| 21,200 | 100 | 89.81 | 50.38 | 1.03 | 1.17 | 1.19 | 1.25 | 1.66 | 1.65 | 0.90 | 1.34 | 1.30 | 1.12 |
| 21,300 | 100 | 119.75 | 50.37 | 1.03 | 1.19 | 1.40 | 1.50 | 1.52 | 1.55 | 1.09 | 1.33 | 1.34 | 1.16 |
| 21,400 | 100 | 159.38 | 51.40 | 1.02 | 1.24 | 1.65 | 1.83 | 1.40 | 1.46 | 1.18 | 1.31 | 1.40 | 1.20 |
| 21,500 | 100 | 69.88 | 70.03 | 1.01 | 1.09 | 0.97 | 0.96 | 1.44 | 1.46 | 0.83 | 1.11 | 1.11 | 1.03 |
| 21,600 | 100 | 89.94 | 70.34 | 1.02 | 1.12 | 1.11 | 1.16 | 1.41 | 1.46 | 0.94 | 1.17 | 1.18 | 1.06 |
| 21,700 | 100 | 119.82 | 70.48 | 9.13 | 1.15 | 1.30 | 1.40 | 1.35 | 1.41 | 1.05 | 1.25 | 1.22 | 1.08 |
| 21,800 | 100 | 159.64 | 70.57 | 1.03 | 1.19 | 1.51 | 1.68 | 1.24 | 1.33 | 1.11 | 1.20 | 1.26 | 1.11 |
| 21,900 | 100 | 199.34 | 70.84 | 1.04 | 1.21 | 1.77 | 1.90 | 1.19 | 1.27 | 1.13 | 1.20 | 1.28 | 1.13 |
| R2 | 0.234674 | 0.994574 | 0.994593 | 0.994436 | |||||||||
| Start Cycle | No. of Cycles | σd | σ3 | K-θ | Rahim and George | Uzan | Universal Witczak | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K1 | K2 | K1 | K2 | K3 | K1 | K2 | K3 | ||||
| 20,100 | 100 | 21.18 | 19.94 | 0.61 | 1.01 | 0.32 | 0.41 | 1.13 | 0.82 | 0.51 | 0.73 | 1.09 | 0.97 |
| 20,200 | 100 | 34.91 | 20.40 | 0.76 | 1.16 | 0.58 | 0.71 | 1.79 | 0.88 | 0.15 | 1.39 | 0.98 | 1.03 |
| 20,300 | 100 | 49.65 | 20.32 | 0.83 | 1.20 | 0.81 | 0.93 | 2.44 | 1.17 | 0.19 | 1.77 | 1.06 | 1.17 |
| 20,400 | 100 | 69.70 | 20.65 | 0.96 | 1.23 | 1.09 | 1.22 | 2.81 | 1.56 | 0.20 | 1.95 | 1.31 | 1.37 |
| 20,500 | 100 | 35.49 | 35.62 | 3.49 | 1.12 | 0.68 | 0.71 | 1.58 | 1.26 | 0.12 | 1.32 | 1.08 | 1.04 |
| 20,600 | 100 | 50.51 | 35.63 | 0.83 | 1.14 | 0.78 | 0.91 | 1.70 | 1.46 | 0.19 | 1.39 | 1.18 | 1.09 |
| 20,700 | 100 | 70.05 | 35.70 | 0.91 | 1.18 | 0.98 | 1.15 | 1.94 | 1.70 | 0.48 | 1.42 | 1.37 | 1.20 |
| 20,800 | 100 | 89.57 | 35.75 | 0.99 | 1.21 | 1.22 | 1.37 | 1.98 | 1.86 | 0.82 | 1.51 | 1.45 | 1.24 |
| 20,900 | 100 | 119.07 | 35.77 | 0.99 | 1.23 | 1.42 | 1.58 | 1.72 | 1.68 | 1.14 | 1.43 | 1.43 | 1.24 |
| 21,000 | 100 | 50.37 | 49.76 | 0.78 | 1.01 | 0.68 | 0.73 | 1.34 | 1.32 | 0.65 | 0.95 | 1.01 | 1.00 |
| 21,100 | 100 | 70.17 | 50.61 | 0.92 | 1.09 | 0.91 | 1.01 | 1.53 | 1.54 | 0.74 | 1.15 | 1.17 | 1.06 |
| 21,200 | 100 | 90.01 | 50.74 | 0.95 | 1.14 | 1.08 | 1.22 | 1.50 | 1.60 | 0.91 | 1.22 | 1.27 | 1.11 |
| 21,300 | 100 | 119.80 | 50.87 | 0.99 | 1.19 | 1.32 | 1.50 | 1.43 | 1.56 | 1.09 | 1.26 | 1.34 | 1.16 |
| 21,400 | 100 | 159.56 | 50.86 | 1.00 | 1.22 | 1.58 | 1.78 | 1.34 | 1.41 | 1.17 | 1.25 | 1.36 | 1.18 |
| 21,500 | 100 | 70.23 | 70.54 | 0.87 | 0.99 | 0.83 | 0.89 | 1.23 | 1.33 | 0.88 | 0.96 | 1.02 | 1.00 |
| 21,600 | 100 | 90.12 | 71.26 | 1.00 | 1.13 | 1.09 | 1.18 | 1.39 | 1.49 | 0.94 | 1.16 | 1.21 | 1.07 |
| 21,700 | 100 | 120.09 | 71.32 | 9.72 | 1.05 | 1.14 | 1.28 | 1.18 | 1.29 | 1.04 | 1.11 | 1.11 | 1.04 |
| 21,800 | 100 | 159.61 | 70.99 | 0.97 | 1.18 | 1.46 | 1.68 | 1.21 | 1.32 | 1.11 | 1.16 | 1.26 | 1.11 |
| 21,900 | 100 | 199.78 | 71.17 | 0.93 | 1.17 | 1.59 | 1.79 | 1.07 | 1.20 | 1.09 | 1.06 | 1.21 | 1.10 |
| R2 | 0.221460 | 0.799531 | 0.800532 | 0.802060 | |||||||||
| Name of Specimen | Soil Classification | OSS Model (ER = K1 τoct − K2) | |||
|---|---|---|---|---|---|
| LST 1331:2022 | USCS | K1 | K2 | R2 | |
| SP1 | Variously graded sand (SP) | Silty sand (SM) | 16.08 | 53.90 | 0.98 |
| SP2 | Variously graded sand (SP) | Poorly graded sand (SP) | 15.60 | 19.46 | 0.99 |
| SP3 | Variously graded sand (SP) | Silty sand (SM) | 15.91 | 37.24 | 0.85 |
| SG1 | Well-graded sand (SG) | Well-graded sand (SW) | 16.09 | 56.29 | 0.99 |
| SG2 | Well-graded sand (SG) | Well-graded sand (SW) | 16.24 | 55.74 | 0.99 |
| SG3 | Well-graded sand (SG) | Well-graded sand (SW) | 15.58 | 77.73 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamošiūnas, T.; Skuodis, Š. Predictive Stress Modeling of Resilient Modulus in Sandy Subgrade Soils. Infrastructures 2023, 8, 29. https://doi.org/10.3390/infrastructures8020029
Tamošiūnas T, Skuodis Š. Predictive Stress Modeling of Resilient Modulus in Sandy Subgrade Soils. Infrastructures. 2023; 8(2):29. https://doi.org/10.3390/infrastructures8020029
Chicago/Turabian StyleTamošiūnas, Tadas, and Šarūnas Skuodis. 2023. "Predictive Stress Modeling of Resilient Modulus in Sandy Subgrade Soils" Infrastructures 8, no. 2: 29. https://doi.org/10.3390/infrastructures8020029
APA StyleTamošiūnas, T., & Skuodis, Š. (2023). Predictive Stress Modeling of Resilient Modulus in Sandy Subgrade Soils. Infrastructures, 8(2), 29. https://doi.org/10.3390/infrastructures8020029






