Calibration of Micromechanical Parameters for the Discrete Element Simulation of a Masonry Arch using Artificial Intelligence
Abstract
:1. Introduction
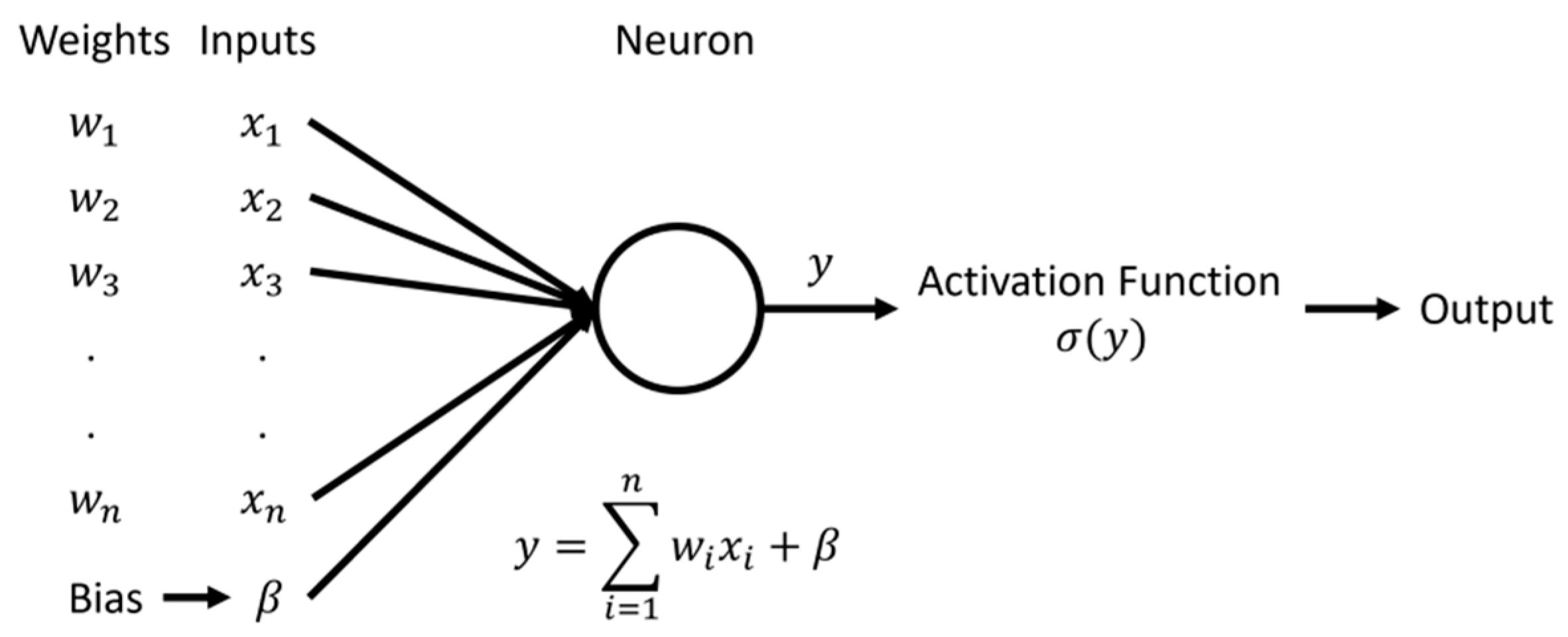
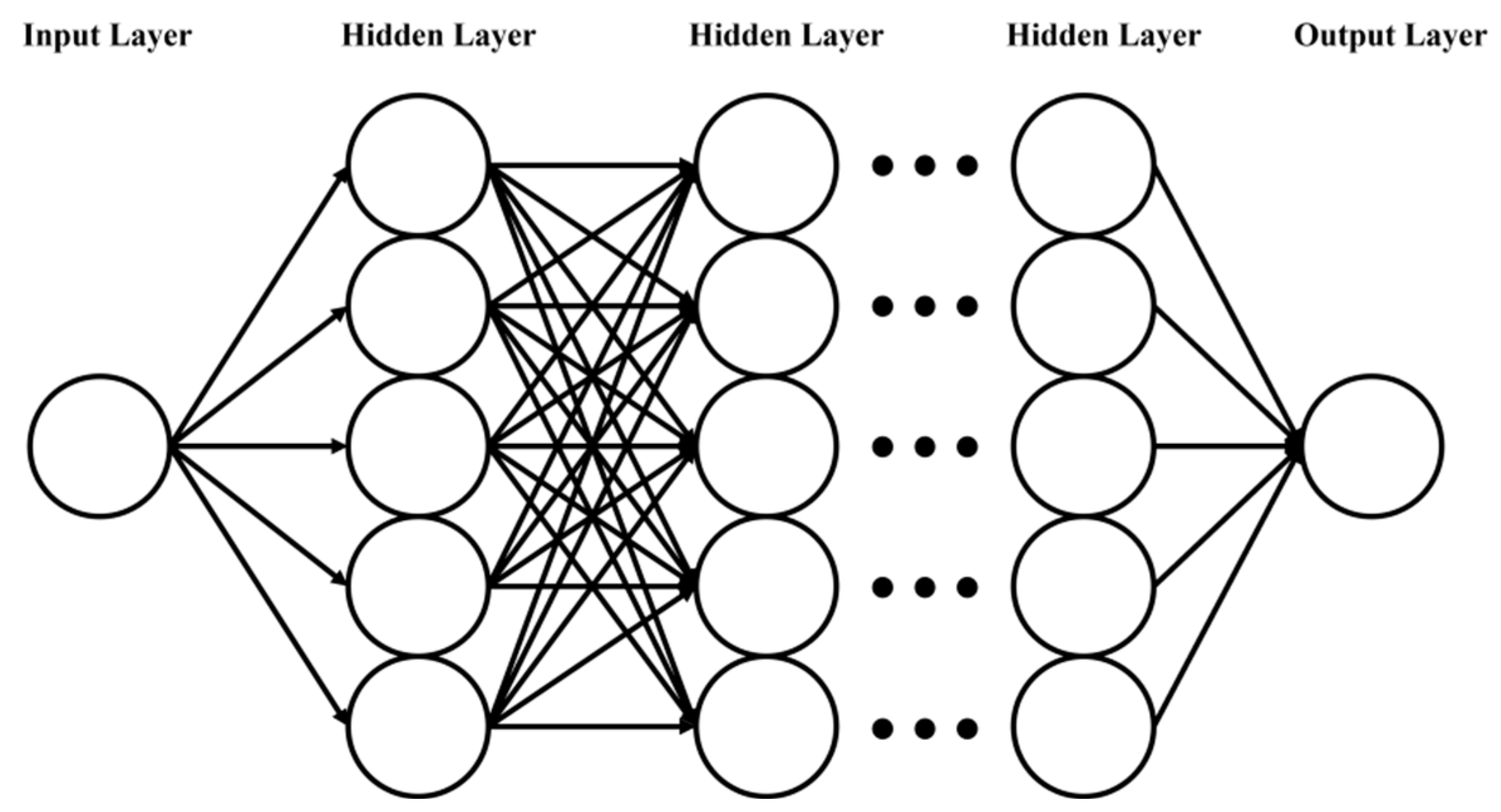
1.1. DEM and Its Applications
1.2. Material Parameters
1.3. Previous Works on Algorithmised Calibration
1.4. Modelling of Masonry Structures
1.5. Aim of Study
2. Prototype Masonry Arch Quasi-Static Experiment and Analysis
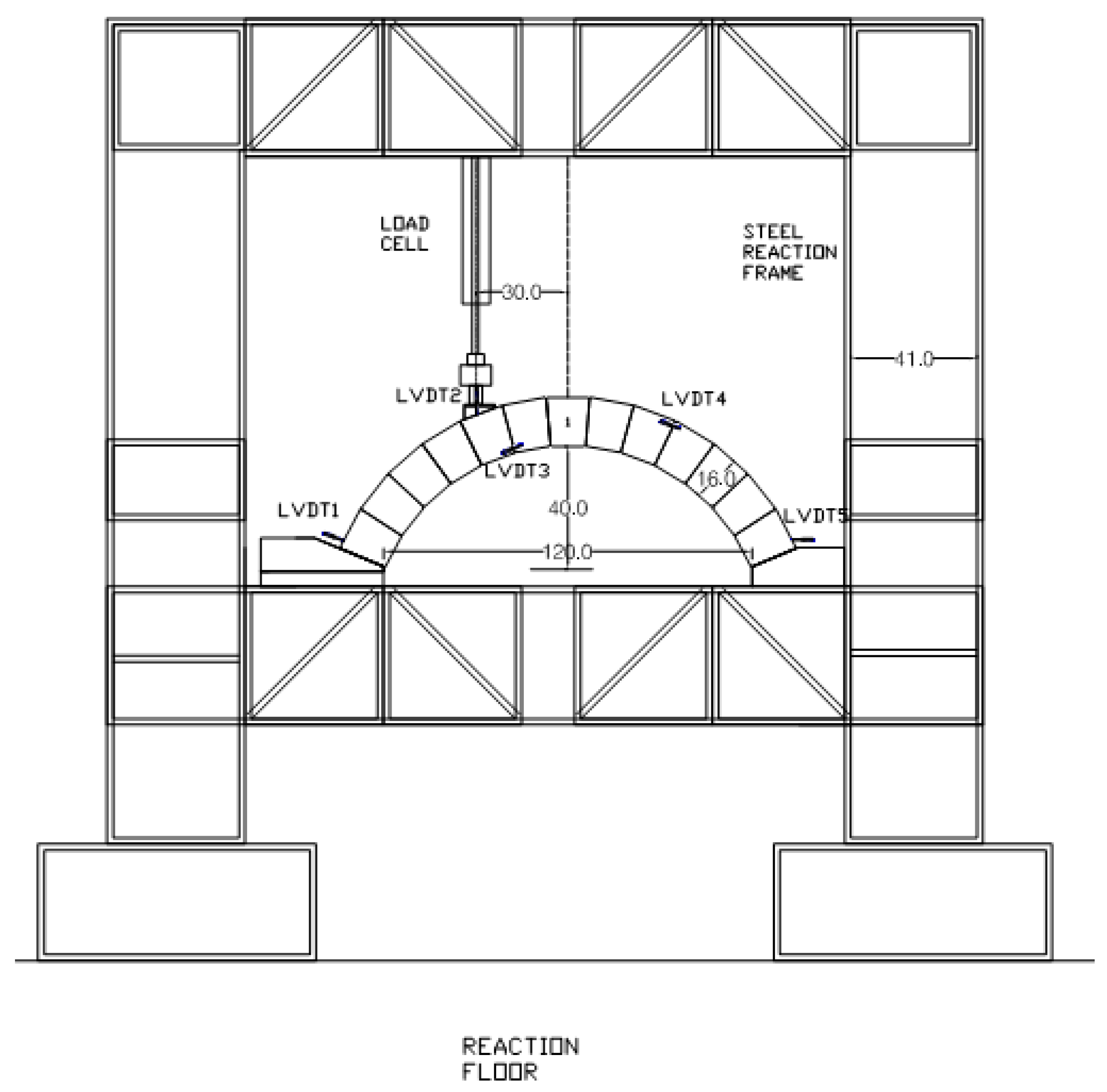
2.1. Experimental Setup of Masonry Arch
2.2. Quasi-Static Experiment and Results
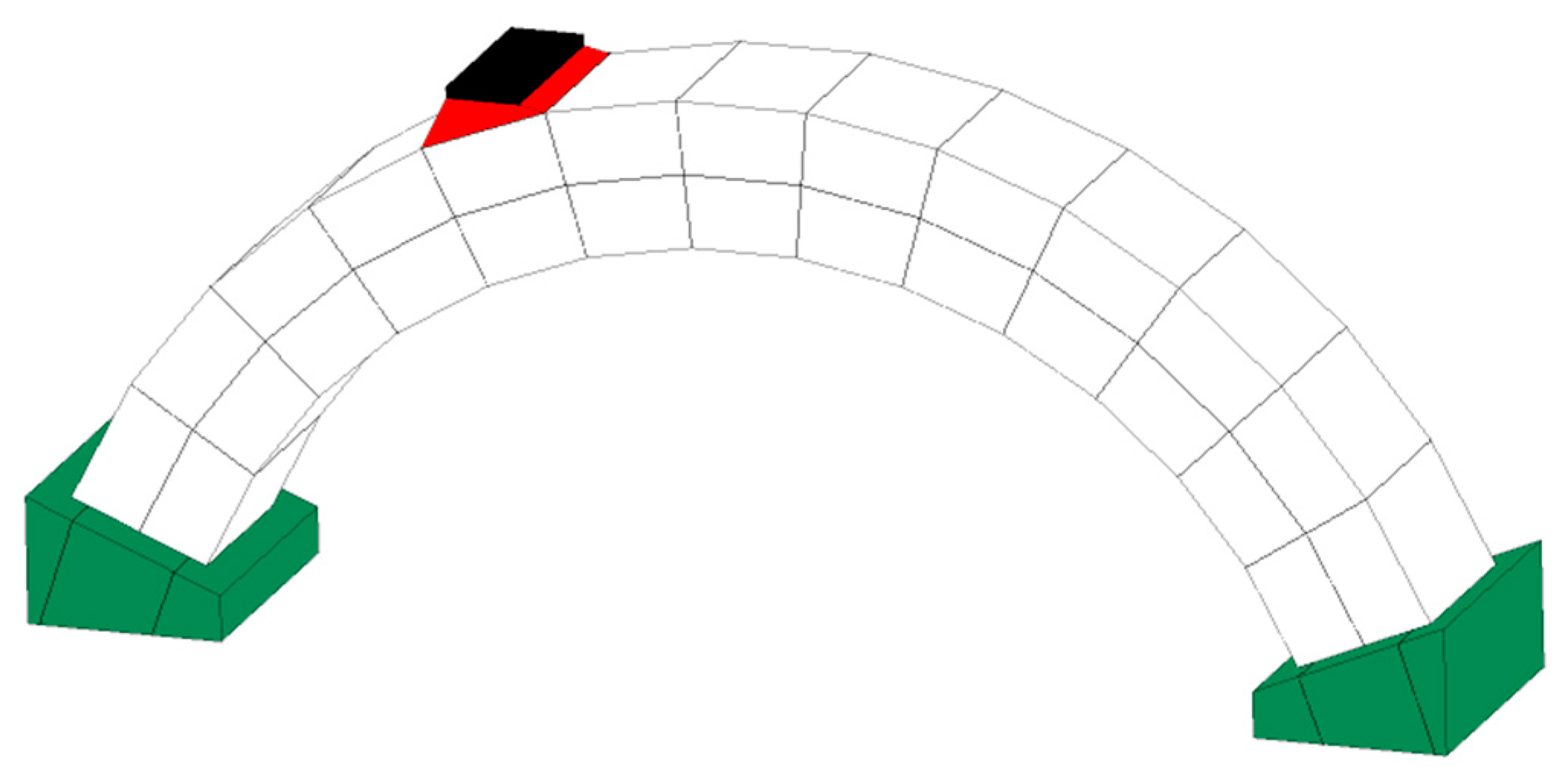
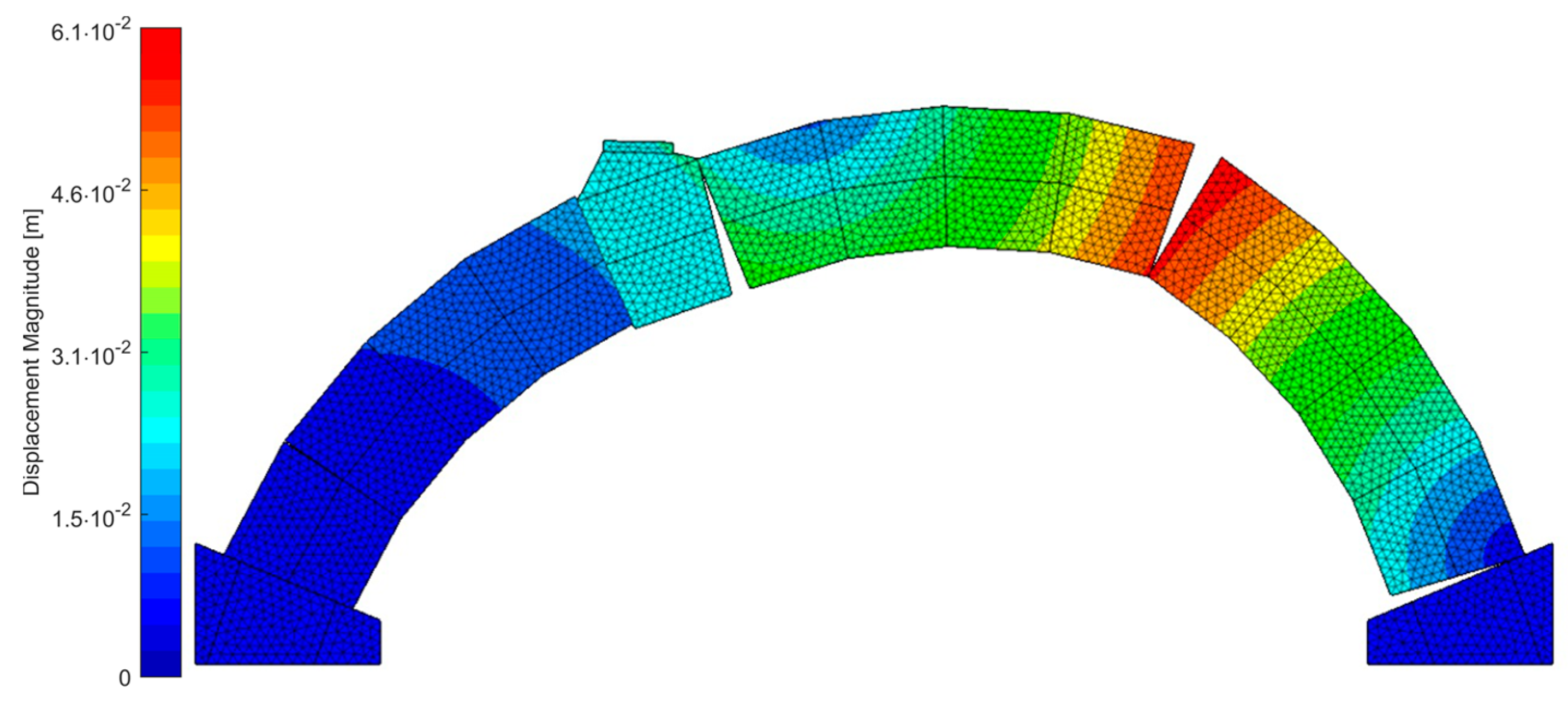
2.3. Discrete Element Modelling of the Quasi-Static Analysis
- Element size along the arch thickness (eight blocks): 10 mm;
- Block material: rigid; eight blocks along the arch thickness (radial direction);
- Loading velocity: 5 mm/s;
- Contact stiffness values: kn = 4 GPa/m; ks = 1.6 Gpa/m;
- Contact friction angle (initial as well as residual): 30.5°.
2.4. Modified Surface Discretisation
2.4.1. Introduction
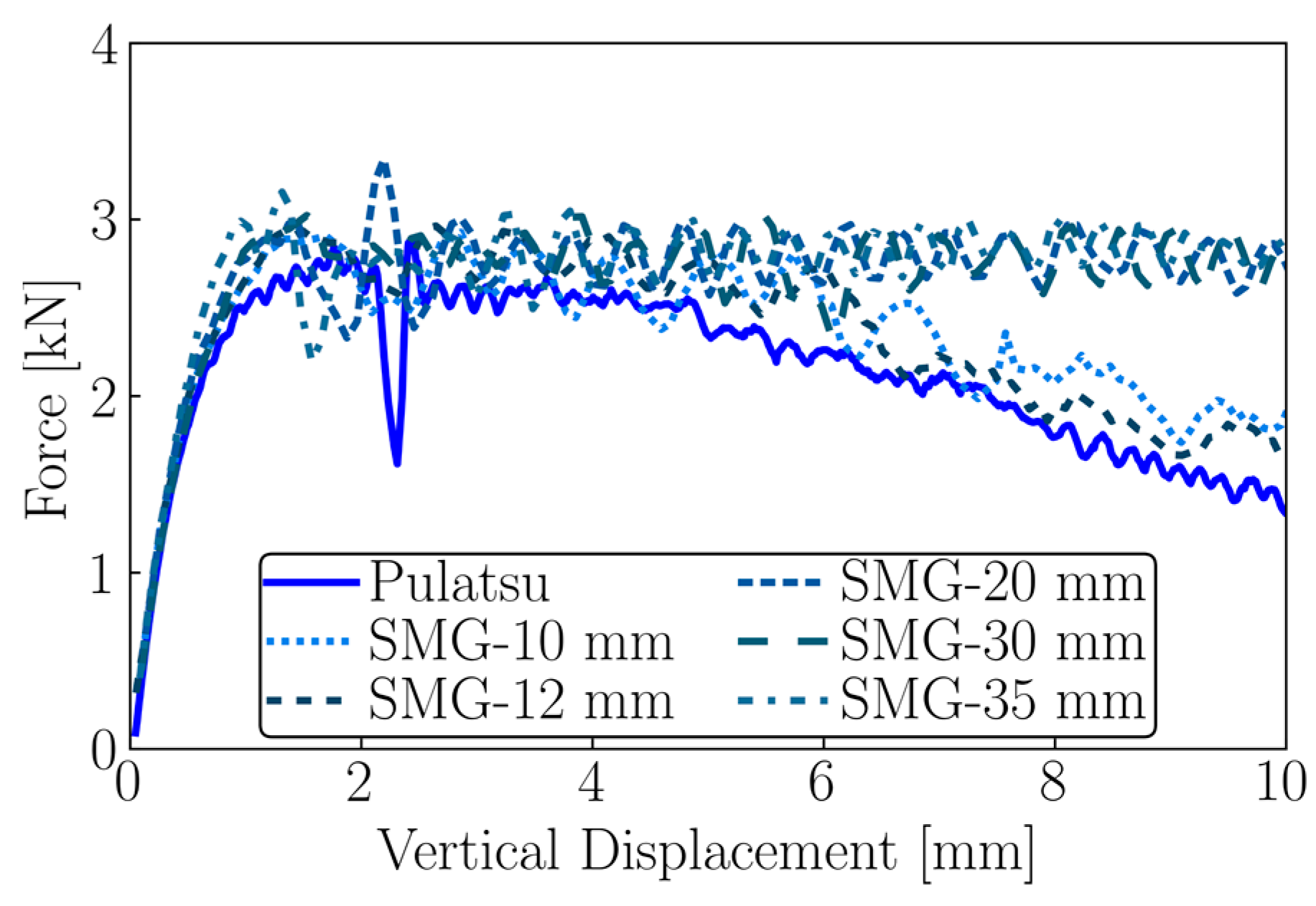
2.4.2. Effect of Loading Velocity
2.4.3. Effect of Mesh Density
3. Calibration Methods for the Model Parameters
3.1. Genetic Algorithm
3.2. Particle Swarm Optimisation
3.3. The Novel Method: TBPSO
3.4. Objective Functions
3.4.1. Objective Function 1
3.4.2. Objective Function 2
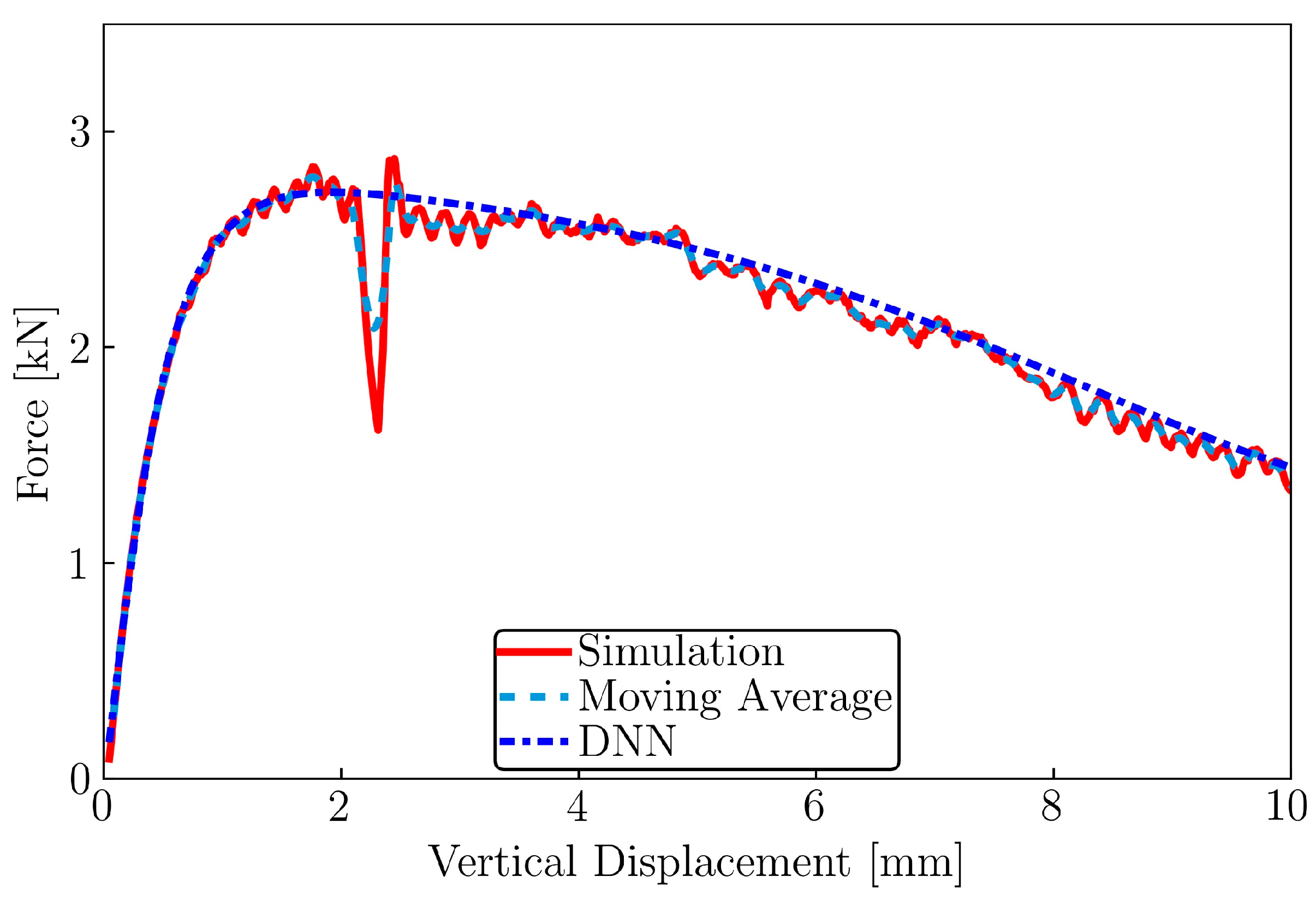
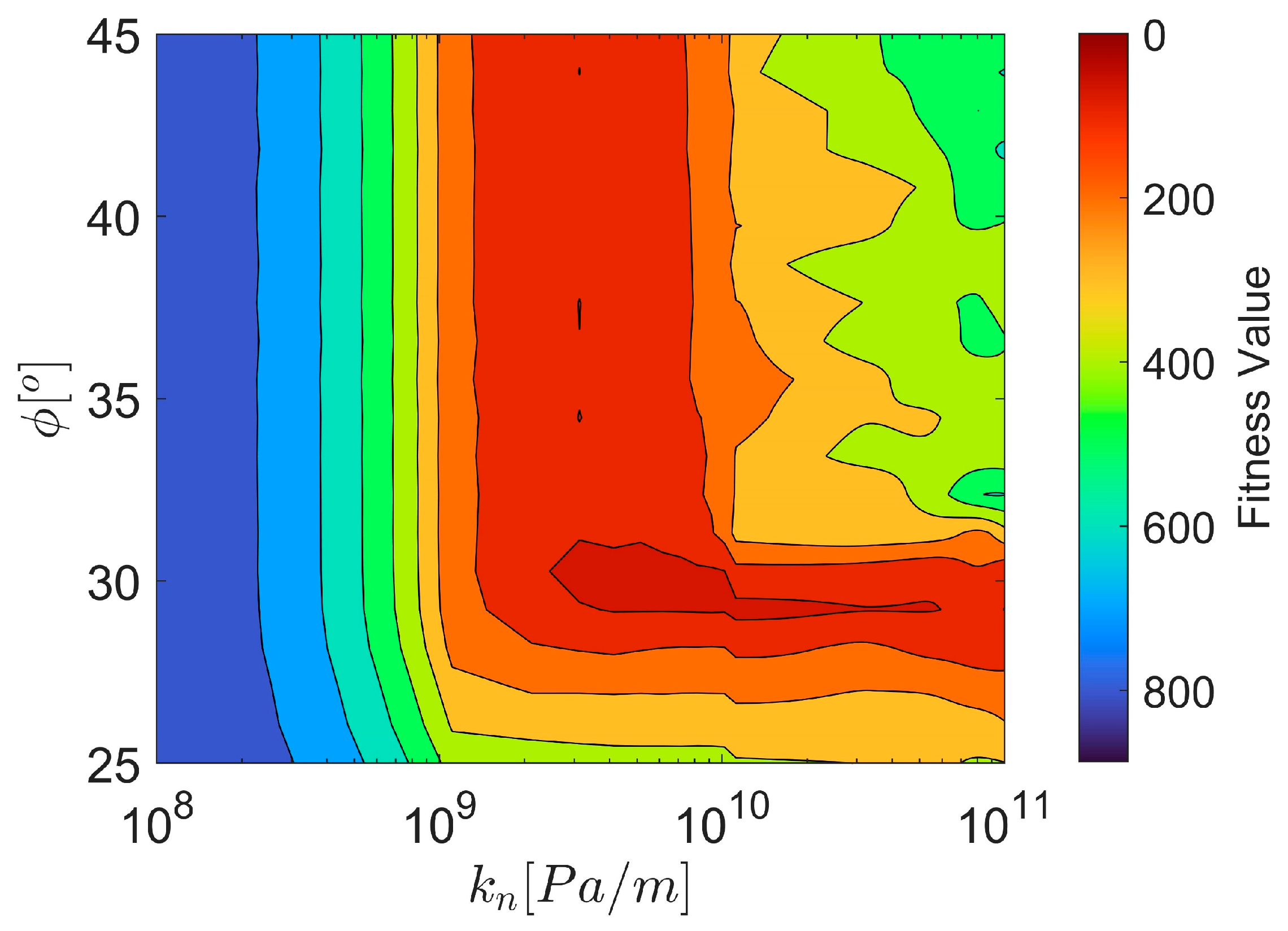
3.4.3. Representation of Objective Function
3.5. Software Background and Workflow
4. Numerical Analysis, Results and Discussion
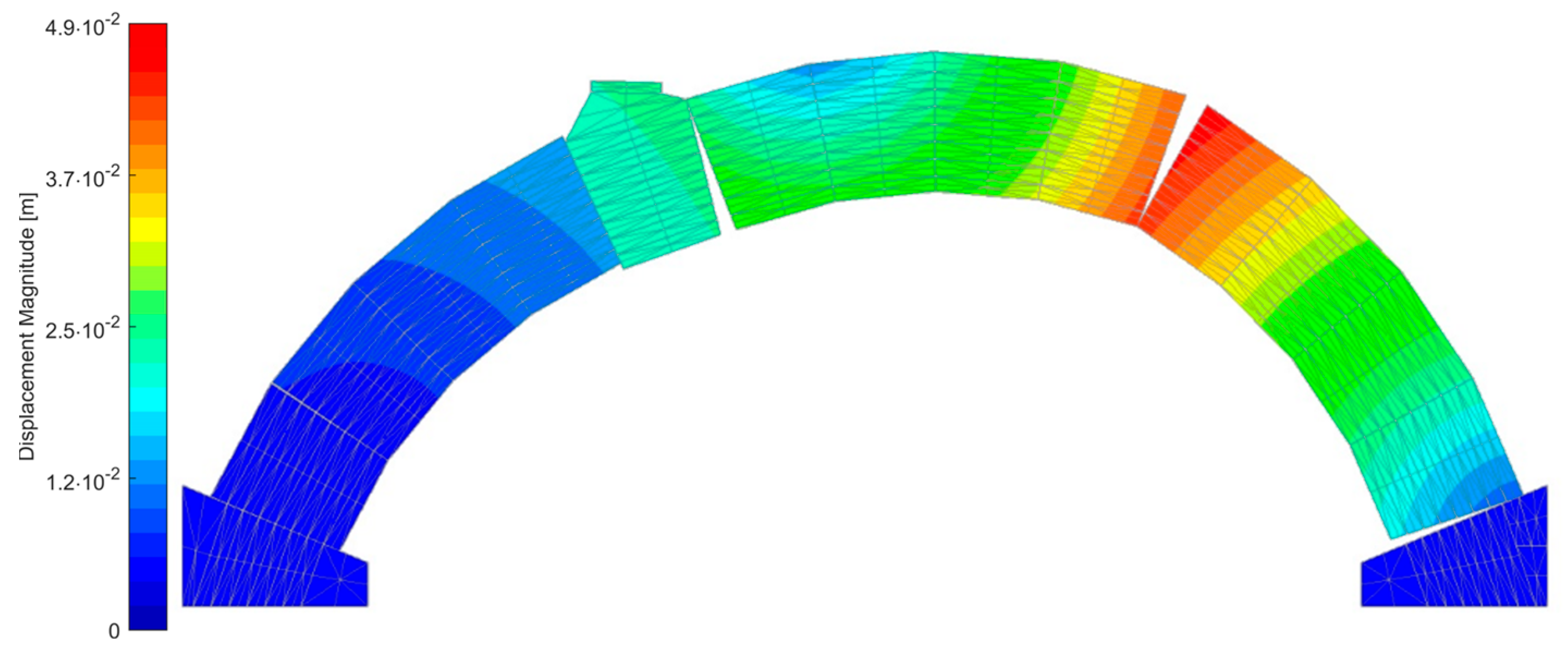
4.1. Pulatsu’s Geometry
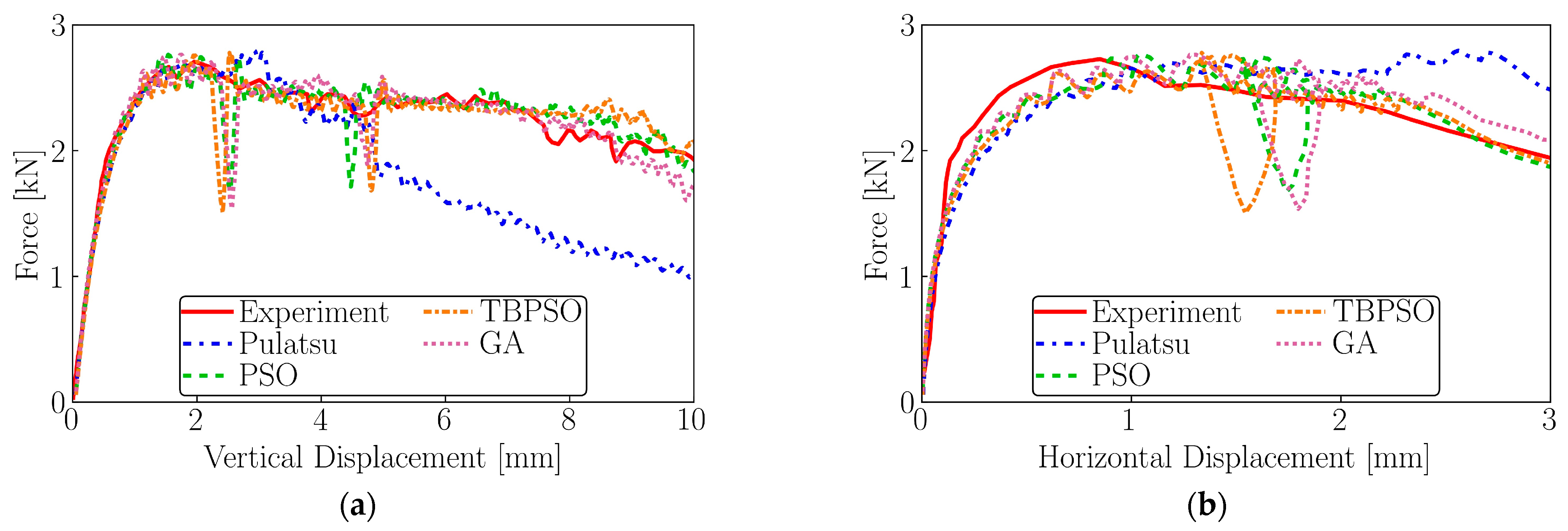
4.1.1. Objective Function 1
4.1.2. Objective Function 2
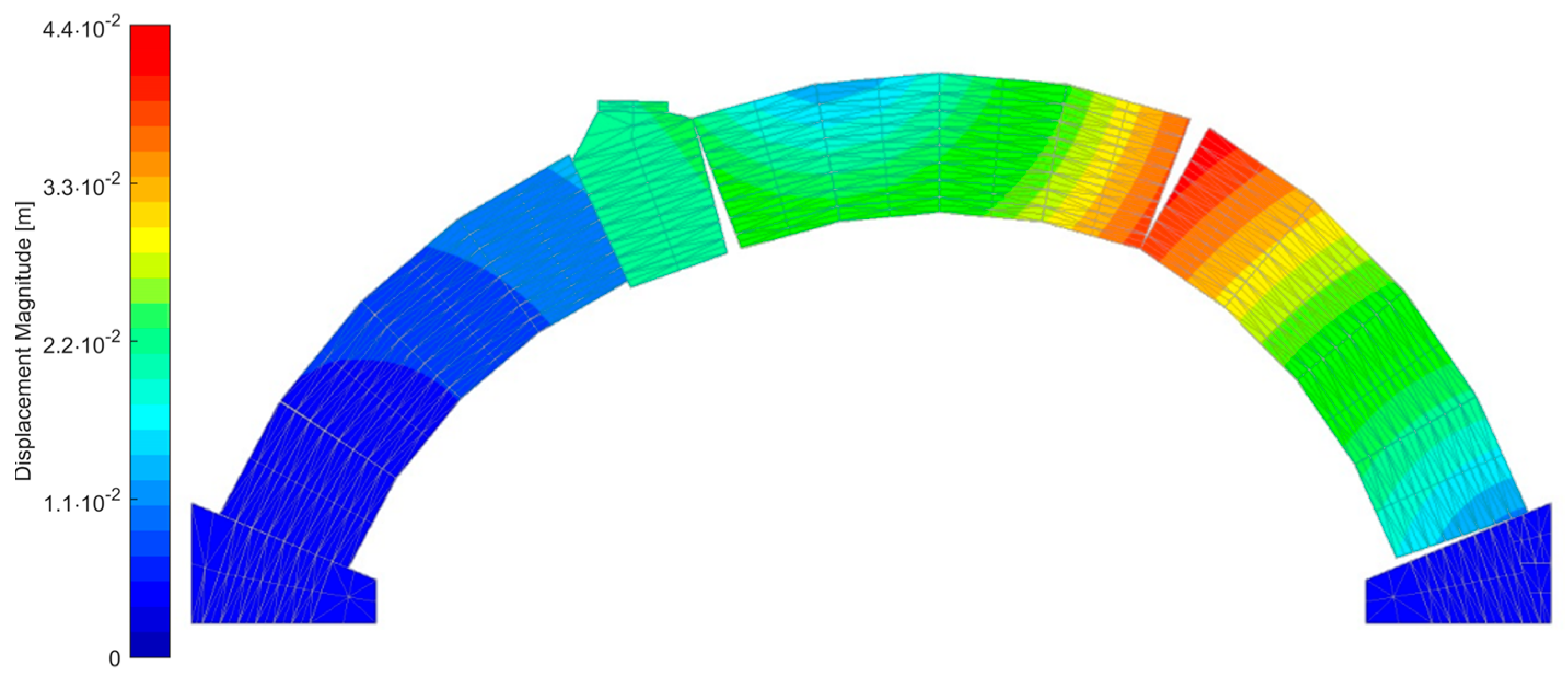
4.2. Surface Densely Meshed Model
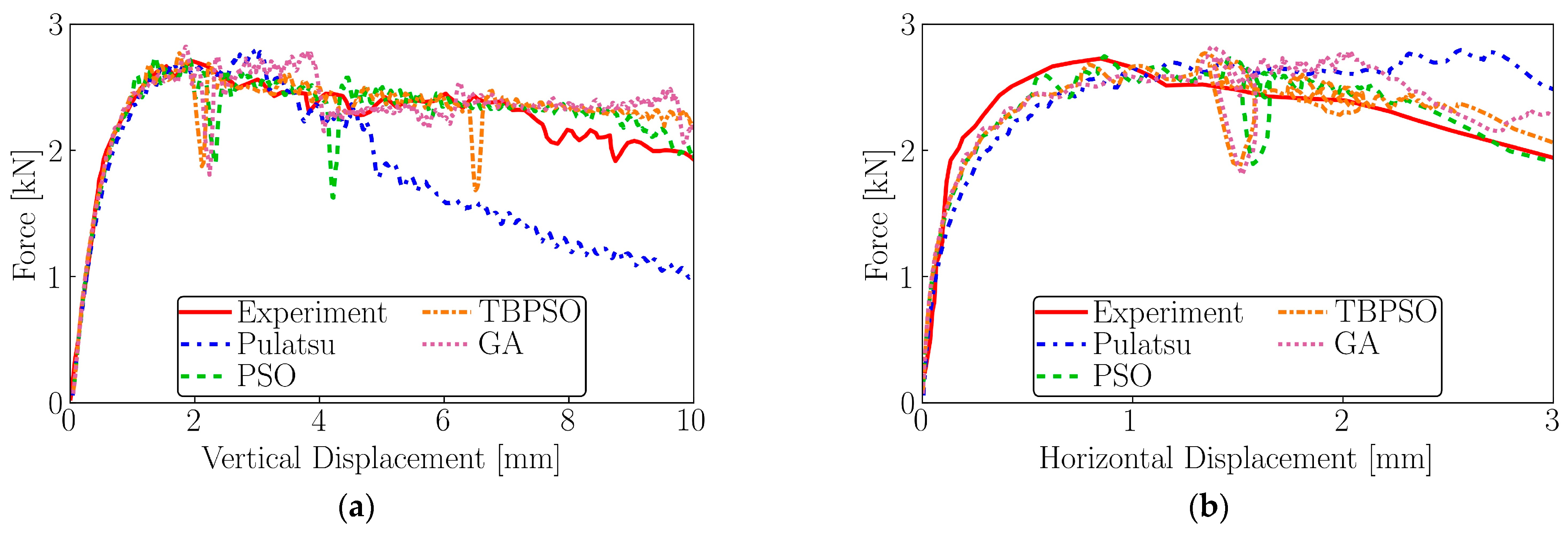
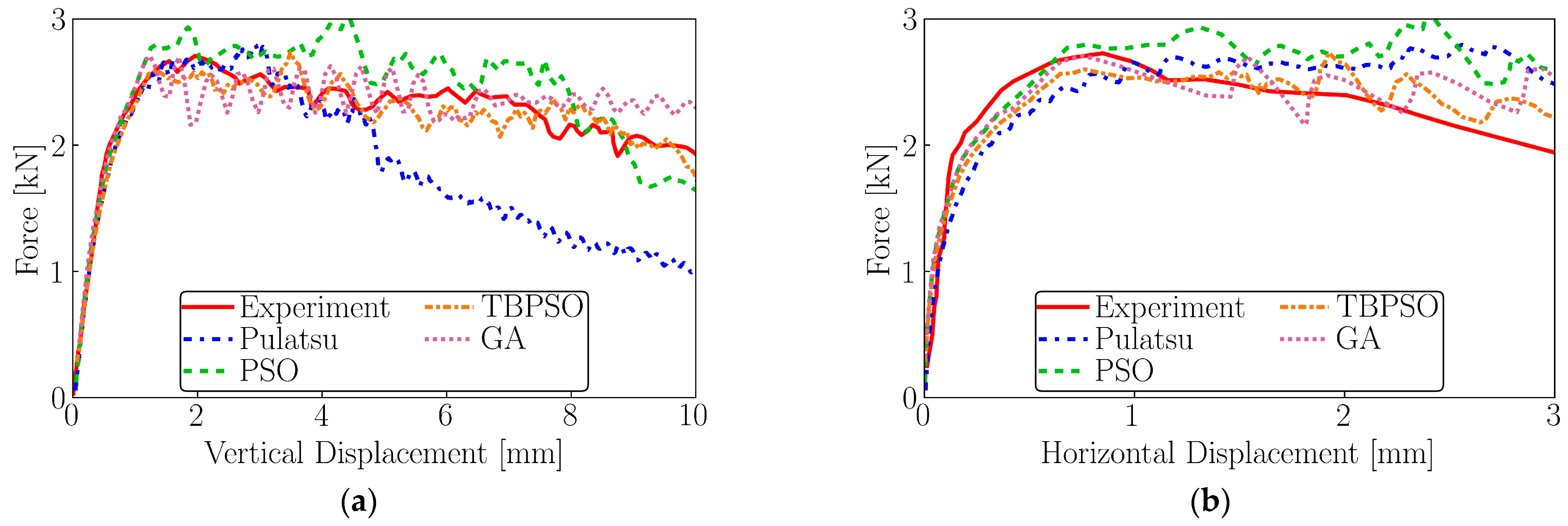
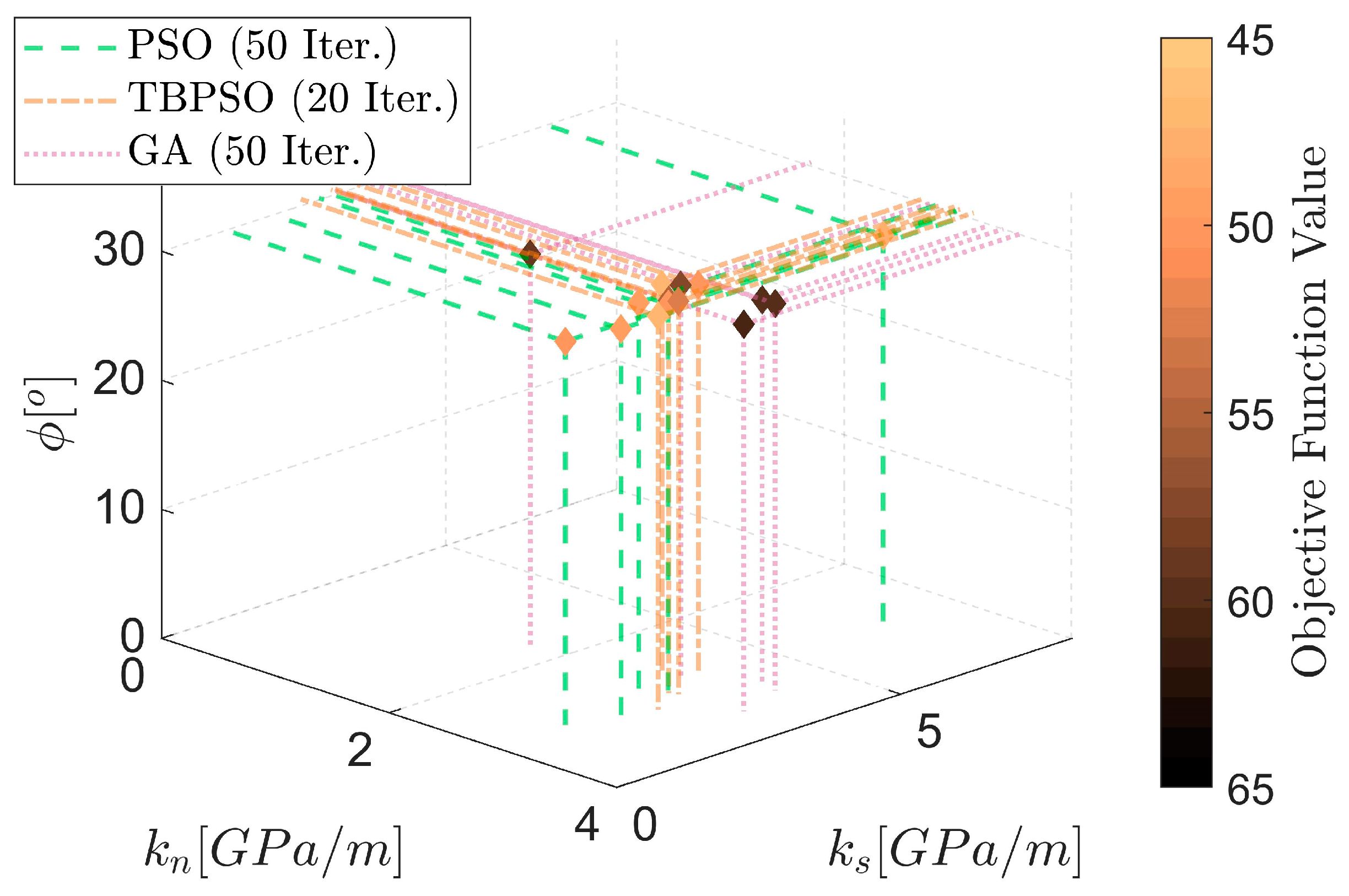
4.2.1. Objective Function 1
4.2.2. Objective Function 2
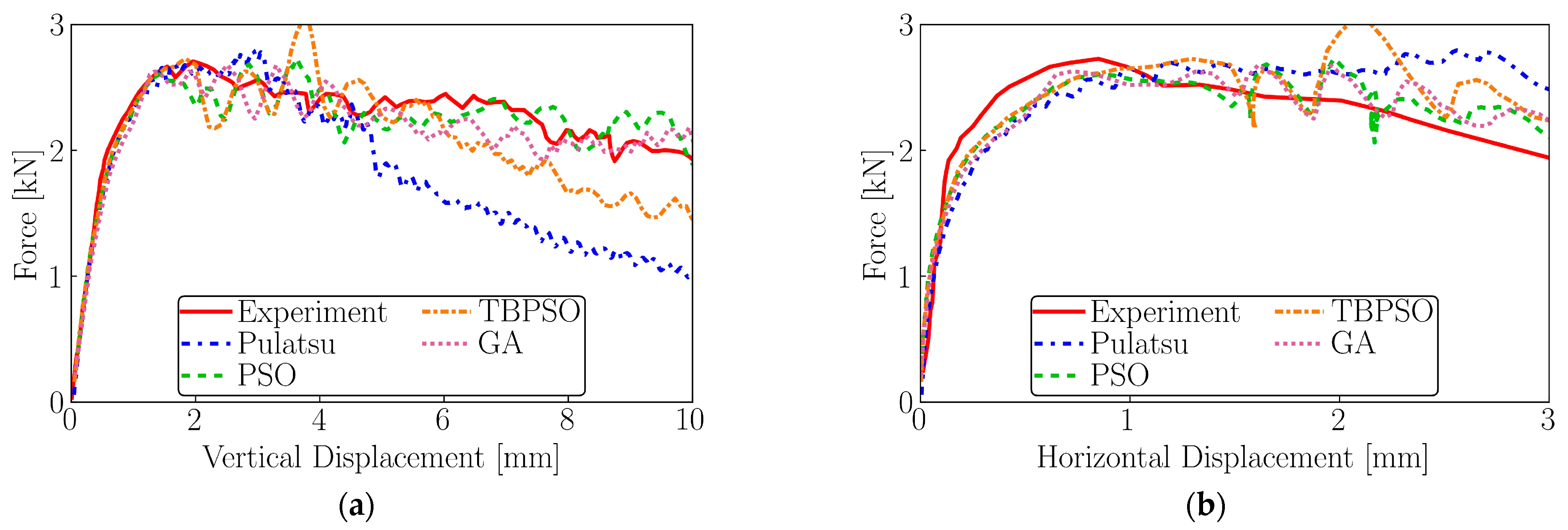
4.2.3. Reduced Loading Plate Velocity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cundall, P.A. A computer model for simulating progressive, large scale movement in blocky rock systems. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971; Volume 2. [Google Scholar]
- Sarhosis, V.; Bagi, K.; Lemos, J.V.; Milani, G. Computational Modeling of Masonry Structures Using the Discrete Element Method; IGI Global: Hershey, PA, USA, 2016. [Google Scholar] [CrossRef]
- Sarhosis, V.; Lemos, J.V.; Bagi, K. Discrete element modeling. In Numerical Modeling of Masonry and Historical Structures; Elsevier: Amsterdam, The Netherlands, 2019; pp. 469–501. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method, 1st ed.; Wiley: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Munjiza, A.; Galić, M.; Smoljanović, H.; Marović, P.; Mihanović, A.; Živaljić, N.; Williams, J.; Avital, E. Aspects of the hybrid finite discrete element simulation technology in science and engineering. Int. J. Eng. Model. 2020, 32, 45–55. [Google Scholar] [CrossRef]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Rackl, M.; Hanley, K.J. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Ben Turkia, S.; Wilke, D.N.; Pizette, P.; Govender, N.; Abriak, N.-E. Benefits of virtual calibration for discrete element parameter estimation from bulk experiments. Granul. Matter 2019, 21, 110. [Google Scholar] [CrossRef]
- Zeng, H.; Xu, W.; Zang, M.; Yang, P.; Guo, X. Calibration and validation of DEM-FEM model parameters using upscaled particles based on physical experiments and simulations. Adv. Powder Technol. 2020, 31, 3947–3959. [Google Scholar] [CrossRef]
- Bhalode, P.; Ierapetritou, M. Discrete element modeling for continuous powder feeding operation: Calibration and system analysis. Int. J. Pharm. 2020, 585, 119427. [Google Scholar] [CrossRef]
- Mohajeri, M.J.; van Rhee, C.; Schott, D.L. Replicating cohesive and stress-history-dependent behavior of bulk solids: Feasibility and definiteness in DEM calibration procedure. Adv. Powder Technol. 2021, 32, 1532–1548. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Spatial Prediction and Kriging. In Statistics for Spatial Data; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 105–209. [Google Scholar] [CrossRef]
- Benvenuti, L.; Kloss, C.; Pirker, S. Identification of DEM simulation parameters by Artificial Neural Networks and bulk experiments. Powder Technol. 2016, 291, 456–465. [Google Scholar] [CrossRef]
- Westbrink, F.; Elbel, A.; Schwung, A.; Ding, S.X. Optimization of DEM parameters using multi-objective reinforcement learning. Powder Technol. 2020, 379, 602–616. [Google Scholar] [CrossRef]
- Do, H.Q.; Aragón, A.M.; Schott, D.L. A calibration framework for discrete element model parameters using genetic algorithms. Adv. Powder Technol. 2018, 29, 1393–1403. [Google Scholar] [CrossRef]
- Mohajeri, M.J.; Do, H.Q.; Schott, D.L. DEM calibration of cohesive material in the ring shear test by applying a genetic algorithm framework. Adv. Powder Technol. 2020, 31, 1838–1850. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; 1st MIT Press, Ed.; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Sarhosis, V. Optimisation procedure for material parameter identification for masonry constitutive models. Int. J. Mason. Res. Innov. 2016, 1, 48–58. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arch. Comput. Methods Eng. 2020, 27, 1153–1185. [Google Scholar] [CrossRef]
- Heyman, J. The stone skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
- Bagi, K. When Heyman’s Safe Theorem of rigid block systems fails: Non-Heymanian collapse modes of masonry structures. Int. J. Solids Struct. 2014, 51, 2696–2705. [Google Scholar] [CrossRef] [Green Version]
- Block, P.; Ochsendorf, J. Thrust Network Analysis: A New Methodology for 3D Equilibrium. J. Int. Assoc. Shell Spat. Struct. 2007, 48, 167–173. [Google Scholar]
- Chiozzi, A.; Milani, G.; Tralli, A. A Genetic Algorithm NURBS-based new approach for fast kinematic limit analysis of masonry vaults. Comput. Struct. 2017, 182, 187–204. [Google Scholar] [CrossRef]
- Nela, B.; Rios, A.J.; Pingaro, M.; Reccia, E.; Trovalusci, P. Masonry Arches Simulations Using Cohesion Parameter as Code Enrichment for Limit Analysis Approach. Int. J. Mason. Res. Innov. 2022, in press. [Google Scholar] [CrossRef]
- Nela, B.; Rios, A.J.; Pingaro, M.; Reccia, E.; Trovalusci, P. Limit analysis of locally reinforced masonry arches. Eng. Struct. 2022, 271, 114921. [Google Scholar] [CrossRef]
- Sinopoli, A.; Rapallini, M.; Smars, P. Plasticity, Coulomb Friction and Sliding in the Limit Analysis of Masonry Arches. In Proceedings of the 4th International Conference on Arch Bridges (ARCH’04), Barcelona, Spain, 17–19 November 2004. [Google Scholar]
- Gilbert, M.; Casapulla, C.; Ahmed, H.M. Limit analysis of masonry block structures with non-associative frictional joints using linear programming. Comput. Struct. 2006, 84, 873–887. [Google Scholar] [CrossRef]
- Casapulla, C.; Argiento, L.U. In-plane frictional resistances in dry block masonry walls and rocking-sliding failure modes revisited and experimentally validated. Compos. Part B Eng. 2018, 132, 197–213. [Google Scholar] [CrossRef]
- Pepe, M.; Pingaro, M.; Trovalusci, P.; Reccia, E.; Leonetti, L. Micromodels for the in-plane failure analysis of masonry walls: Limit Analysis, FEM and FEM/DEM approaches. Frat. E Integrità Strutt. 2019, 14, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Pulatsu, B.; Gonen, S.; Zonno, G. Static and Impact Response of a Single-Span Stone Masonry Arch. Infrastructures 2021, 6, 178. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95 Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. Swarm Intell. 1995, 1, 33–57. [Google Scholar] [CrossRef]
- Birhane, T.H. Blast Analysis of Railway Masonry Bridges. M.Sc. Thesis, University of Minho, Braga, Portugal, 2009. [Google Scholar]
- Vasconcelos, G. Experimental Investigations on the Mechanics of Stone Masonry: Characterization of Granites and Behavior of Ancient Masonry Shear Walls. Ph.D. Thesis, University of Minho, Braga, Portugal, 2005. [Google Scholar]
- Pulatsu, B.; Bretas, E.M.; Lourenco, P.B. Discrete element modeling of masonry structures: Validation and application. Earthq. Struct. 2016, 11, 563–582. [Google Scholar] [CrossRef]
- Godio, M.; Stefanou, I.; Sab, K. Effects of the dilatancy of joints and of the size of the building blocks on the mechanical behavior of masonry structures. Meccanica 2018, 53, 1629–1643. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Oliveira, D.V.; Roca, P.; Orduña, A. Dry Joint Stone Masonry Walls Subjected to In-Plane Combined Loading. J. Struct. Eng. 2005, 131, 1665–1673. [Google Scholar] [CrossRef] [Green Version]
- Pulatsu, B.; Gonen, S.; Erdogmus, E.; Lourenço, P.B.; Lemos, J.V.; Prakash, R. In-plane structural performance of dry-joint stone masonry Walls: A spatial and non-spatial stochastic discontinuum analysis. Eng. Struct. 2021, 242, 112620. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Ramos, L.F. Characterization of Cyclic Behavior of Dry Masonry Joints. J. Struct. Eng. 2004, 130, 779–786. [Google Scholar] [CrossRef]
- Reza, B.M.; Zbigniew, M. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.H.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings IEEE World Congress on Computational Intelligence (Cat No98TH8360), Anchorage, AK, USA, 4–9 May 1998. [Google Scholar] [CrossRef]
- Bergh, F.V.D. An Analysis of Particle Swarm Optimizers. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2002. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation CEC00 (Cat No00TH8512), La Jolla, CA, USA, 16–19 July 2000. [Google Scholar] [CrossRef]
- Chatterjee, A.; Siarry, P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization. Comput. Oper. Res. 2006, 33, 859–871. [Google Scholar] [CrossRef]
- Clerc, M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat No 99TH8406), Washington, DC, USA, 6–9 July 1999. [Google Scholar] [CrossRef]
- Kar, R.; Mandal, D.; Bardhan, S.; Ghoshal, S.P. Optimization of linear phase FIR band pass filter using Particle Swarm Optimization with Constriction Factor and Inertia Weight Approach. In Proceedings of the 2011 IEEE Symposium on Industrial Electronics and Applications, Langkawi, Malaysia, 25–28 September 2011. [Google Scholar] [CrossRef]
- Huang, W.M.; Deng, Z.R.; Li, R.H.; Tang, X.X. Trust-Based Particle Swarm Optimization for Grid Task Scheduling. Appl. Mech. Mater. 2012, 239–240, 1331–1335. [Google Scholar] [CrossRef]
- Deng, L. Deep Learning: Methods and Applications. Found. Trends Signal Process 2013, 7, 197–387. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]






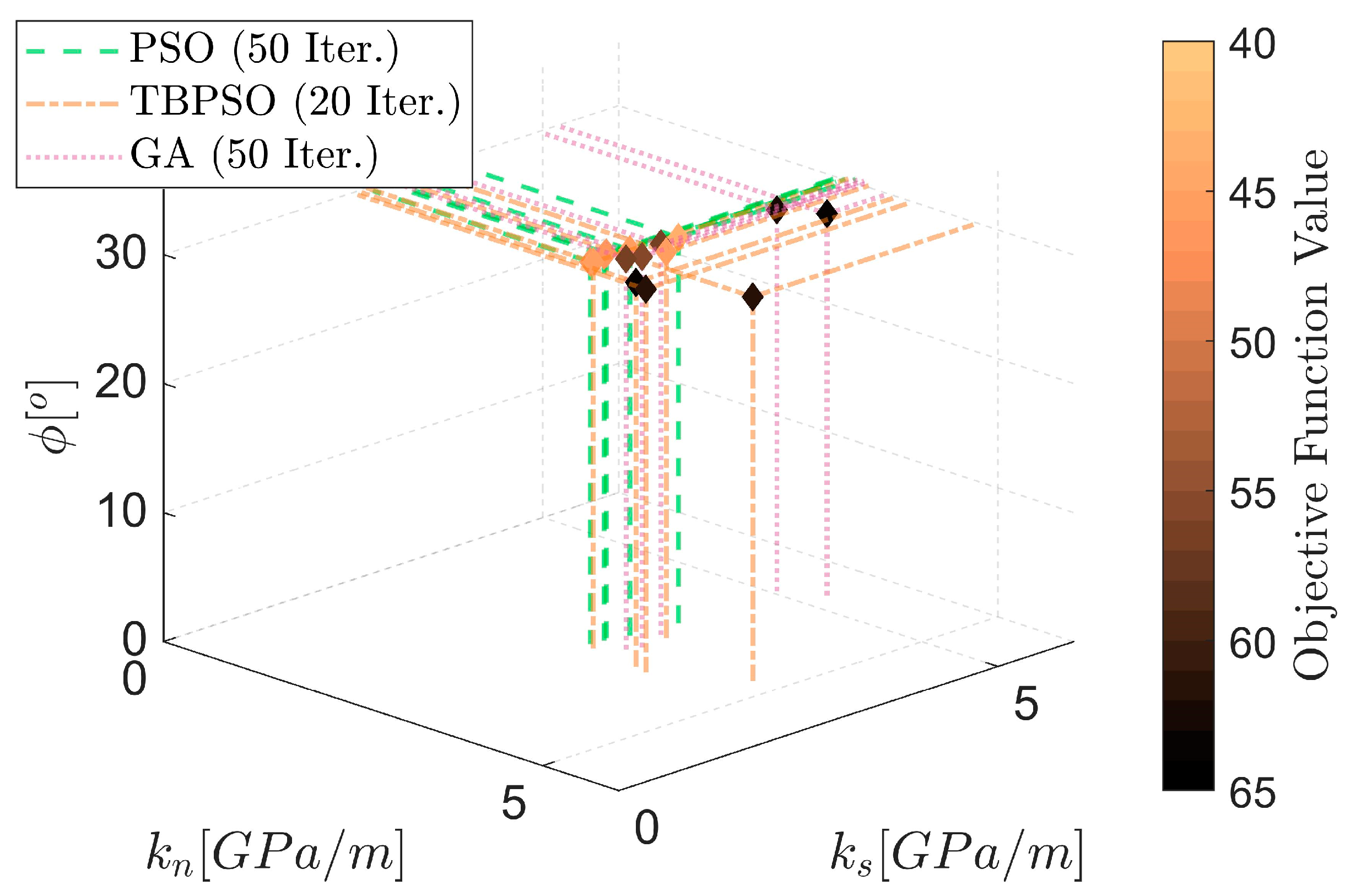

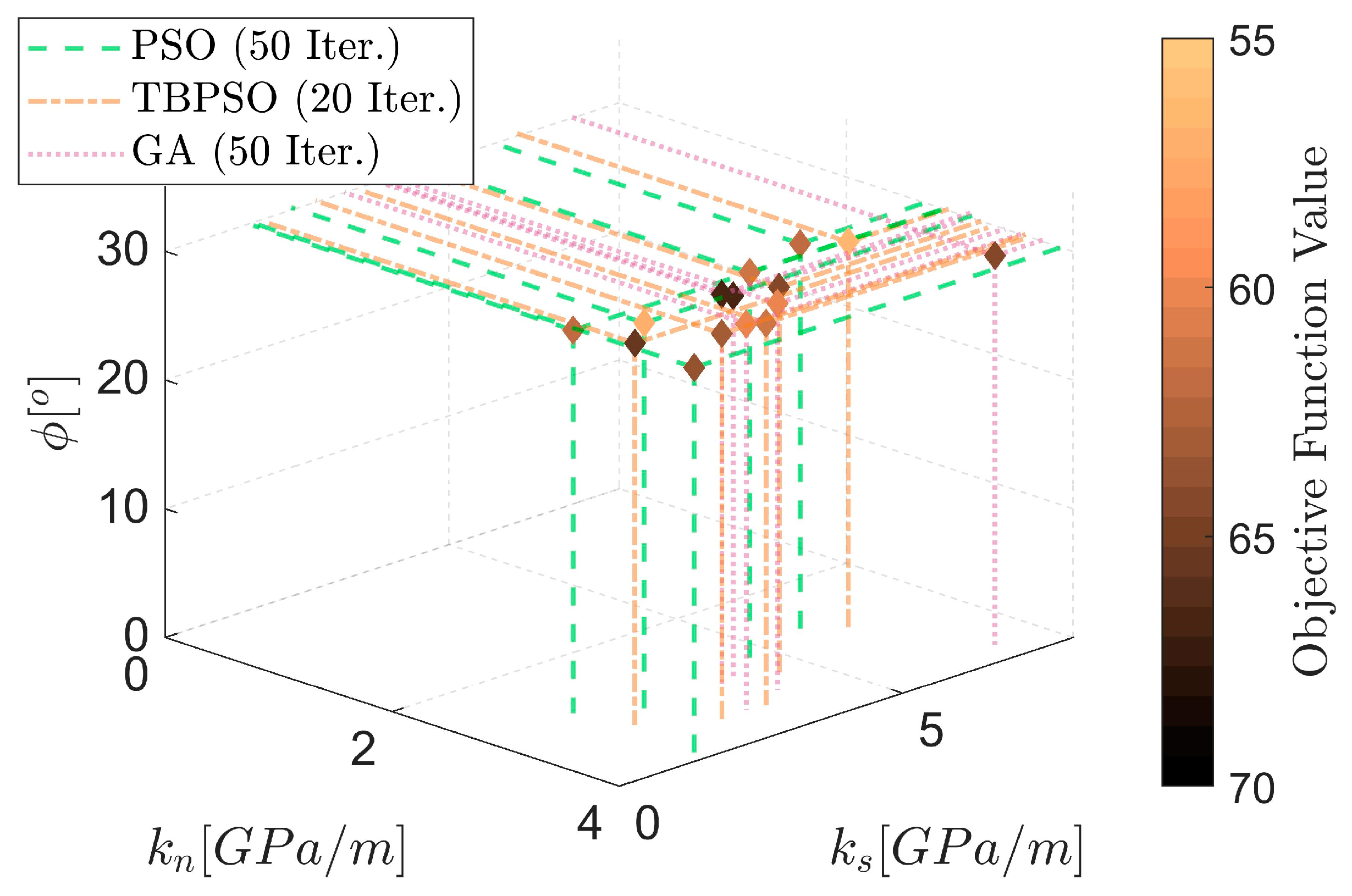


| Calibration Process | Number of Iterations | Run ID | kn (GPa/m) | ks (GPa/m) | ϕ (°) | Fitness (-) |
|---|---|---|---|---|---|---|
| PSO | 50 | 1 | 3.13 | 3.66 | 30.31 | 43.4 |
| 2 | 2.99 | 3.16 | 30.05 | 45.9 | ||
| 3 | 2.89 | 2.92 | 29.89 | 46.0 | ||
| 4 | 2.87 | 2.76 | 29.63 | 46.7 | ||
| 5 | 2.85 | 2.99 | 29.83 | 46.9 | ||
| GA | 50 | 1 | 3.30 | 3.01 | 30.40 | 55.0 |
| 2 | 3.20 | 3.36 | 30.50 | 56.0 | ||
| 3 | 3.24 | 2.86 | 30.40 | 56.3 | ||
| 4 | 3.09 | 5.00 | 29.80 | 62.0 | ||
| 5 | 3.53 | 5.22 | 29.90 | 63.0 | ||
| PSO | 20 | 1 | 4.17 | 1.17 | 29.67 | 63.3 |
| 2 | 4.02 | 1.44 | 29.83 | 63.7 | ||
| 3 | 4.42 | 1.00 | 29.78 | 64.9 | ||
| 4 | 3.09 | 2.54 | 34.68 | 82.4 | ||
| 5 | 3.24 | 3.47 | 39.11 | 85.0 | ||
| TBPSO | 20 | 1 | 3.03 | 2.64 | 30.16 | 45.4 |
| 2 | 3.30 | 3.33 | 30.15 | 45.8 | ||
| 3 | 3.80 | 2.56 | 29.70 | 61.1 | ||
| 4 | 4.68 | 3.09 | 29.78 | 61.9 | ||
| 5 | 3.62 | 2.61 | 29.79 | 63.1 |
| Calibration Process | Number of Iterations | Run ID | kn (GPa/m) | ks (GPa/m) | ϕ (°) | Fitness (-) |
|---|---|---|---|---|---|---|
| PSO | 50 | 1 | 3.18 | 3.58 | 30.19 | 43.4 |
| 2 | 3.34 | 3.26 | 30.27 | 44.9 | ||
| 3 | 3.24 | 2.70 | 30.23 | 45.9 | ||
| 4 | 3.40 | 3.49 | 30.25 | 46.1 | ||
| 5 | 3.37 | 2.80 | 30.32 | 46.3 | ||
| GA | 50 | 1 | 3.13 | 6.68 | 30.2 | 43.9 |
| 2 | 3.05 | 4.15 | 30.2 | 47.7 | ||
| 3 | 2.44 | 4.35 | 30.0 | 54.9 | ||
| 4 | 3.38 | 5.73 | 30.1 | 60.2 | ||
| 5 | 2.54 | 2.97 | 30.1 | 63.7 | ||
| PSO | 20 | 1 | 3.90 | 2.38 | 30.55 | 60.0 |
| 2 | 3.40 | 3.15 | 29.97 | 61.0 | ||
| 3 | 2.93 | 1.95 | 30.08 | 63.1 | ||
| 4 | 5.30 | 0.82 | 29.78 | 65.5 | ||
| 5 | 3.20 | 1.69 | 36.40 | 90.2 | ||
| TBPSO | 20 | 1 | 3.31 | 3.37 | 30.18 | 43.8 |
| 2 | 3.22 | 3.21 | 30.30 | 45.5 | ||
| 3 | 3.42 | 3.63 | 30.45 | 50.5 | ||
| 4 | 3.40 | 2.29 | 30.41 | 53.4 | ||
| 5 | 3.56 | 2.10 | 30.35 | 56.9 |
| Calibration Process | Number of Iterations | Run ID | kn (Gpa/m) | ks (Gpa/m) | ϕ (°) | Fitness (-) |
|---|---|---|---|---|---|---|
| PSO | 50 | 1 | 3.11 | 2.22 | 30.20 | 57.3 |
| 2 | 2.92 | 4.46 | 30.33 | 61.4 | ||
| 3 | 2.82 | 1.55 | 29.76 | 61.7 | ||
| 4 | 2.70 | 5.79 | 30.03 | 61.9 | ||
| 5 | 3.89 | 1.54 | 29.97 | 63.9 | ||
| GA | 50 | 1 | 3.40 | 3.99 | 30.00 | 59.9 |
| 2 | 3.54 | 3.16 | 30.00 | 60.4 | ||
| 3 | 3.75 | 7.12 | 30.20 | 64.6 | ||
| 4 | 3.10 | 3.61 | 30.40 | 66.5 | ||
| 5 | 3.03 | 3.95 | 29.60 | 66.8 | ||
| PSO | 20 | 1 | 3.27 | 3.33 | 30.01 | 66.0 |
| 2 | 7.00 | 0.94 | 28.78 | 67.9 | ||
| 3 | 6.76 | 0.51 | 28.53 | 68.9 | ||
| 4 | 2.11 | 3.23 | 37.38 | 108.2 | ||
| 5 | 2.49 | 2.45 | 36.71 | 112.4 | ||
| TBPSO | 20 | 1 | 2.92 | 6.20 | 30.20 | 56.3 |
| 2 | 3.56 | 3.47 | 29.68 | 61.2 | ||
| 3 | 3.58 | 2.65 | 30.10 | 63.4 | ||
| 4 | 3.19 | 4.44 | 30.00 | 64.2 | ||
| 5 | 3.25 | 1.78 | 29.66 | 65.7 |
| Calibration Process | Number of Iterations | Run ID | kn (GPa/m) | ks (GPa/m) | ϕ (°) | Fitness (-) |
|---|---|---|---|---|---|---|
| PSO | 50 | 1 | 2.99 | 6.71 | 30.19 | 48.1 |
| 2 | 3.07 | 1.94 | 30.04 | 49.0 | ||
| 3 | 2.81 | 2.77 | 30.13 | 49.1 | ||
| 4 | 2.98 | 2.95 | 30.23 | 50.0 | ||
| 5 | 2.94 | 1.22 | 29.74 | 50.5 | ||
| GA | 50 | 1 | 2.79 | 3.55 | 30.31 | 57.4 |
| 2 | 1.71 | 3.06 | 30.30 | 59.1 | ||
| 3 | 3.24 | 4.08 | 29.70 | 59.4 | ||
| 4 | 3.40 | 3.99 | 30.00 | 59.9 | ||
| 5 | 3.54 | 3.16 | 30.00 | 60.4 | ||
| PSO | 20 | 1 | 6.78 | 0.56 | 29.64 | 57.5 |
| 2 | 4.66 | 0.62 | 29.61 | 58.1 | ||
| 3 | 4.96 | 2.69 | 29.45 | 63.2 | ||
| 4 | 2.43 | 2.84 | 36.49 | 71.7 | ||
| 5 | 3.67 | 0.25 | 29.32 | 110.7 | ||
| TBPSO | 20 | 1 | 3.14 | 2.45 | 30.50 | 46.7 |
| 2 | 2.68 | 3.44 | 30.21 | 47.4 | ||
| 3 | 2.84 | 3.76 | 30.18 | 50.4 | ||
| 4 | 3.02 | 3.05 | 30.43 | 52.2 | ||
| 5 | 2.97 | 2.98 | 30.48 | 54.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kibriya, G.; Orosz, Á.; Botzheim, J.; Bagi, K. Calibration of Micromechanical Parameters for the Discrete Element Simulation of a Masonry Arch using Artificial Intelligence. Infrastructures 2023, 8, 64. https://doi.org/10.3390/infrastructures8040064
Kibriya G, Orosz Á, Botzheim J, Bagi K. Calibration of Micromechanical Parameters for the Discrete Element Simulation of a Masonry Arch using Artificial Intelligence. Infrastructures. 2023; 8(4):64. https://doi.org/10.3390/infrastructures8040064
Chicago/Turabian StyleKibriya, Ghulam, Ákos Orosz, János Botzheim, and Katalin Bagi. 2023. "Calibration of Micromechanical Parameters for the Discrete Element Simulation of a Masonry Arch using Artificial Intelligence" Infrastructures 8, no. 4: 64. https://doi.org/10.3390/infrastructures8040064
APA StyleKibriya, G., Orosz, Á., Botzheim, J., & Bagi, K. (2023). Calibration of Micromechanical Parameters for the Discrete Element Simulation of a Masonry Arch using Artificial Intelligence. Infrastructures, 8(4), 64. https://doi.org/10.3390/infrastructures8040064







