Track Deterioration Model—State of the Art and Research Potentials

Abstract

Track deterioration models (TDMs) help to allocate maintenance work (direct costs) to vehicle runs. Furthermore, these models demonstrate the impact of rolling stock properties on infrastructure. This paper review provides an overview of the state of the art in railway track deterioration modelling and outlines the research potential in this domain. The main focus lies on ballast degradation, rail surface wear and fatigue, and their description in an empiric analytic wear formula. The basis for discussion is the wear formula of the Graz University of Technology. While the TDM demonstrates effectiveness, enhancements are sought, particularly with regard to adjusting the track parameters that vary across railway networks. Further exploration aims to refine the description of rail surface wear and rolling contact fatigue (RCF), incorporating factors such as traction energy and short-wave effects and adapting mathematical functions such as the t-Gamma function. This review underscores the need for ongoing research to develop TDMs that are both simple and detailed enough to encourage track-friendly rolling stock design.

1. Introduction

Existing Track Deterioration Models aim to link vehicles’ input on tracks with the deterioration or damage of track components. All these models have two common basic principles: (1) The damage terms describe an average situation, as they are based on empirical and, thus, statistical analyses, so varying boundary conditions, especially track conditions, are not addressed. (2) The aim of these models is foremost to allocate track costs accordingly to vehicle properties and train speeds. Thus, the models need to support usability for this main task and, consequently, focus on the main or dominant effects and mechanisms. Using such models or single damage terms for the modelling deterioration of tracks and/or their components needs both challenging the results achieved with the averaged approaches with measured in situ conditions and adopting the analytic damage mechanisms based on these findings. This paper provides an overview on the most frequently used damage mechanisms on ballasted tracks and discusses possible adoptions, further developments and adjustments.

This review is structured as follows:

• The model’s methodology is explained in Section 2.
• The motivation and aim can be found in Section 3.
• A declaration of the foundations and alternative/further approaches of the damage terms:

  ▪

  D1 (ballast deterioration in straight and curved lines) is conducted in Section 4,

  ▪

  D2 (rail fatigue in straight lines) is conducted in Section 5,

  ▪

  D3 (rail wear in straight lines) is conducted in Section 6, and

  ▪

  D4 (rail wear and fatigue in curved lines) can be found in Section 7.

• A discussion of the future potential of each deterioration term is explored in Section 8.
• The conclusion is given in Section 9.

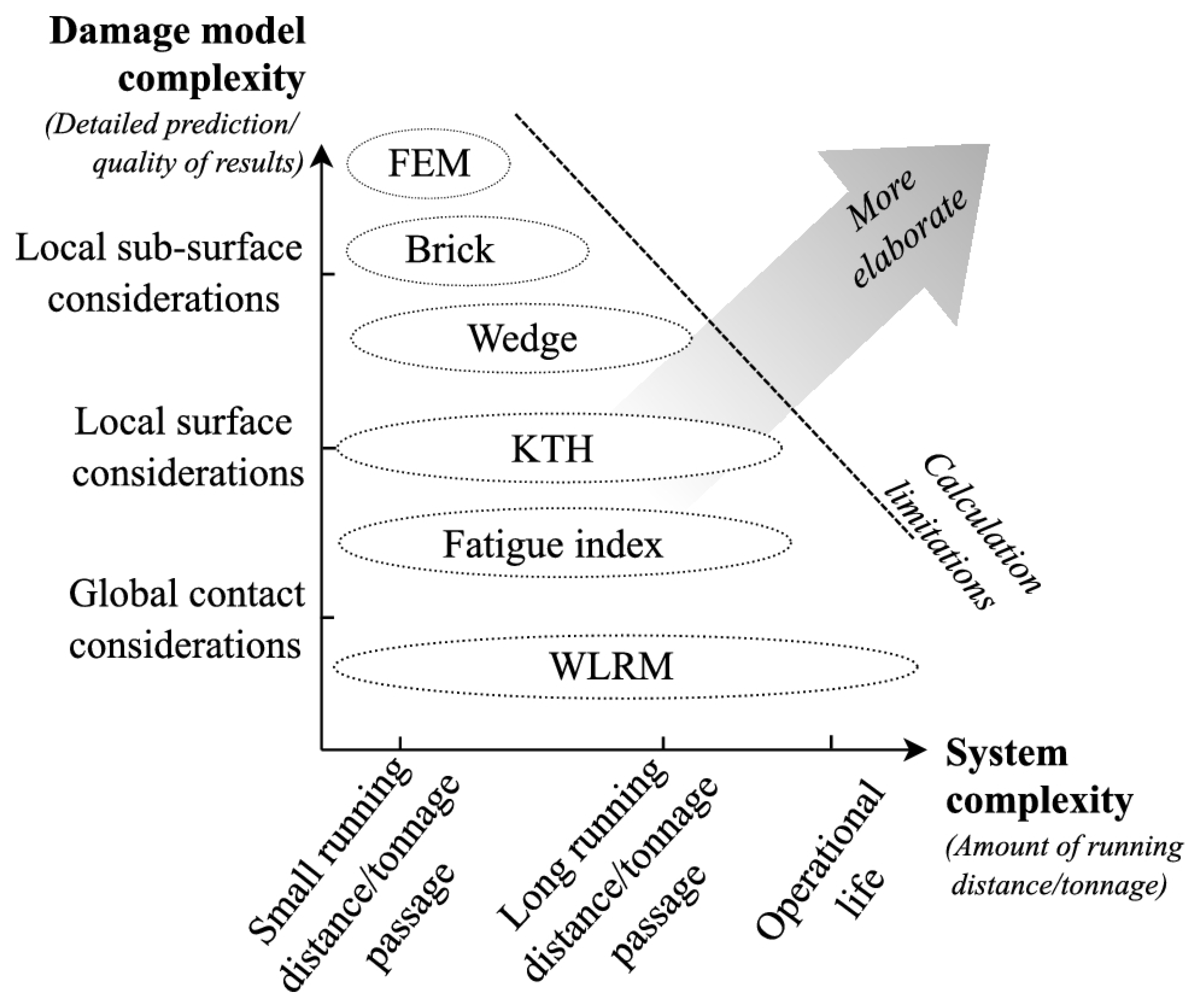
2. Methodology of the TUG Track Deterioration Model

The Track Deterioration Model (TDM) this paper focuses on is published and explained in depth by Marschnig et al. [1]. The discussed model is a further development of and is based on the Swiss TDM that was implemented in the network of the Swiss Federal Railways (SBB) as a track access charging tool in 2017 [2]. However, the former model was implemented by the Graz University of Technology (TUG) in cooperation with the Swiss Federal Railways. Since then, the TUG has added two more terms to the damage function (D6 and D7).

The basic idea of this TDM is to combine maintenance costs, frequencies, and investment costs with empiric-analytical descriptions of track component deterioration on ballasted tracks, which include vehicle and infrastructure parameters in their formulas. In Equation (1), the general methodology of the TUG TDM is depicted. The aim of this formula is to calculate/estimate the total costs per vehicle kilometre that are induced by a certain vehicle on a certain track segment. As the damage terms $D_n$ consist of different units, maintenance and investment costs are recalculated as “cost calibration factors” ($c_1$ to $c_6$ for maintenance costs and $c_7$ for investment costs). These cost calibration factors have, therefore, different units that fit to the according damage term $D_n$. The product of each $D_n\times c_n$ lead to costs per kilometre. Further details on the general model approach and the cost calibration factors $c_n$ can be found in [1,3], as this review focuses on the description of damage mechanisms on ballasted tracks and, therefore, on the damage terms $D_n$. In Equation (2), the complete wear formula is depicted, whereas in Equation (3), an equation of units is added to clarify the methodology of the TUG TDM.

$${\mathrm{C}}_{{\mathrm{V}\mathrm{e}\mathrm{h}}_{\mathrm{S},\mathrm{R}}}=\sum _{\mathrm{n}=1}^7{\mathrm{c}}_{\mathrm{n}}\times {\mathrm{D}}_{\mathrm{n}}$$

(1)

$$\begin{gathered} C_{{Veh}_{S,R}}=c_1\times \stackrel{D1}{\overbrace{{P_{2,S}}^3}}+c_2\times \stackrel{D2}{\overbrace{{P_{2,S}}^{1.2}}}+c_3\times \stackrel{D3}{\overbrace{\mathit{TPV}}}+c_{4.1}\times D4.1+c_{4.2}\times D4.2 \\ +c_5\times \stackrel{D5}{\overbrace{\sqrt{\left(0.5 \times {P_{2,S}}^2+0.5 \times {Y_R}^2\right)}}}+c_6\times \stackrel{D6}{\overbrace{{P_{1,S}}^3}} \\ +c_7\times \stackrel{D7}{\overbrace{{\sqrt{\left(f_{7_{1,R}} \times {{ P}_{2,S}}^2+f_{7_{2,R}} \times {Y_R}^2\right)}}^3}} \end{gathered}$$

(2)

Equation of units:

$$\begin{gathered} \stackrel{C_{Veh}}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}}\right]}}=\stackrel{c_1}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}\times {\mathrm{k}\mathrm{N}}^3}\right]}}\times \stackrel{D1}{\overbrace{\left[{\mathrm{k}\mathrm{N}}^3\right]}}+\stackrel{c_2}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}\times {\mathrm{k}\mathrm{N}}^{1.2}}\right]}}\times \stackrel{D2}{\overbrace{\left[{\mathrm{k}\mathrm{N}}^{1.2}\right]}} \\ +\stackrel{c_3}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}\times \mathrm{k}\mathrm{W}/{\mathrm{m}\mathrm{m}}^2}\right]}}\times \stackrel{D3}{\overbrace{\left[\mathrm{k}\mathrm{W}/{\mathrm{m}\mathrm{m}}^2\right]}}+\stackrel{c_{4.1}}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}}\right]}}\times \stackrel{D4.1}{\overbrace{[-]}} \\ +\stackrel{c_{4.2}}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}}\right]}}\times \stackrel{D4.2}{\overbrace{[-]}}+\stackrel{c_5}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}\times \mathrm{k}\mathrm{N}}\right]}}\times \stackrel{D5}{\overbrace{\left[\mathrm{k}\mathrm{N}\right]}}+\stackrel{c_6}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}\times {\mathrm{k}\mathrm{N}}^3}\right]}}\times \stackrel{D6}{\overbrace{\left[{\mathrm{k}\mathrm{N}}^3\right]}} \\ +\stackrel{c_7}{\overbrace{\left[\frac{costs}{\mathrm{k}\mathrm{m}\times {\mathrm{k}\mathrm{N}}^3}\right]}}\times \stackrel{D7}{\overbrace{\left[{\mathrm{k}\mathrm{N}}^3\right]}} \end{gathered}$$

(3)

$C_{{Veh}_{S,R}}$	costs per vehicle kilometre depending on speed and radius	costs/km
$c_n$	cost calibration factor (n = 1, 2, 3, 4.1, 4.2, 5, 6, 7)	costs/(km unit *)
$D_n$	damage term (n = 1, 2, 3, 4.1, 4.2, 5, 6, 7)	Unit *
$P_{2,S}$	dynamic vertical wheel force (long-waved)	kN
$P_{1,S}$	dynamic vertical wheel force (short-waved)	kN
$Y_R$	lateral force of the guiding wheel on the outer rail within radius R	kN
$TPV$	traction power value	kW/mm2
$D4.1$	damage index for rolling contact fatigue (RCF)	-
$D4.2$	damage index for plastic deformation/rail abrasion	-
$f_{7_{1,R}}$	weighting factor for vertical dynamic wheel force depending on radius R	-
$f_{7_{2,R}}$	weighting factor for lateral wheel force depending on radius R	-
* Unit of the damage term: kN3 for D1, D6 and D7, kN1.2 for D2, kW/mm2 for D3, kN for D5, and D4.1 and D4.2 are dimensionless

In the TUG TDM, every track deterioration term $D_n$ in Equation (2) represents the description of a specific track component damage or wear that leads to track component maintenance (D1–D6). The deterioration of vertical track geometry (ballast bed), wear and damage of the rail surface, and wear of turnout components are covered in this approach.

Table 1. Overview of TUG’s TDM damage terms with their deterioration description.

Dn	Description	Track Curvature
D1	Track geometry and ballast deterioration	Straight and curved
D2	Rail surface fatigue due to vertical force	Straight
D3	Rail surface wear due to traction power	Straight
D4.1	Rail surface fatigue	Curved
D4.2	Rail surface wear	Curved
D5	Wear of turnout components: switch, guard rail, and sleeper	Independent 1
D6	Wear of turnout component: crossing nose	Independent 2
D7	Track renewal (ballast, sleeper, and rail)	Straight and curved

¹ D5 is calculated at 40 km/h and radius 190 m. ² D6 corresponds to the average speed in a certain track segment.

gives an overview of each damage term with a description of its component damage. Furthermore, the model distinguishes between track curvature.

The model approach with its methodology (combining maintenance and investment costs with damage calculations) enables the estimation of track damage costs caused by a vehicle run over the track. Due to this model approach, the track deterioration values and cost calibration factors vary under the following vehicle and infrastructure parameters, as well as maintenance actions and frequencies:

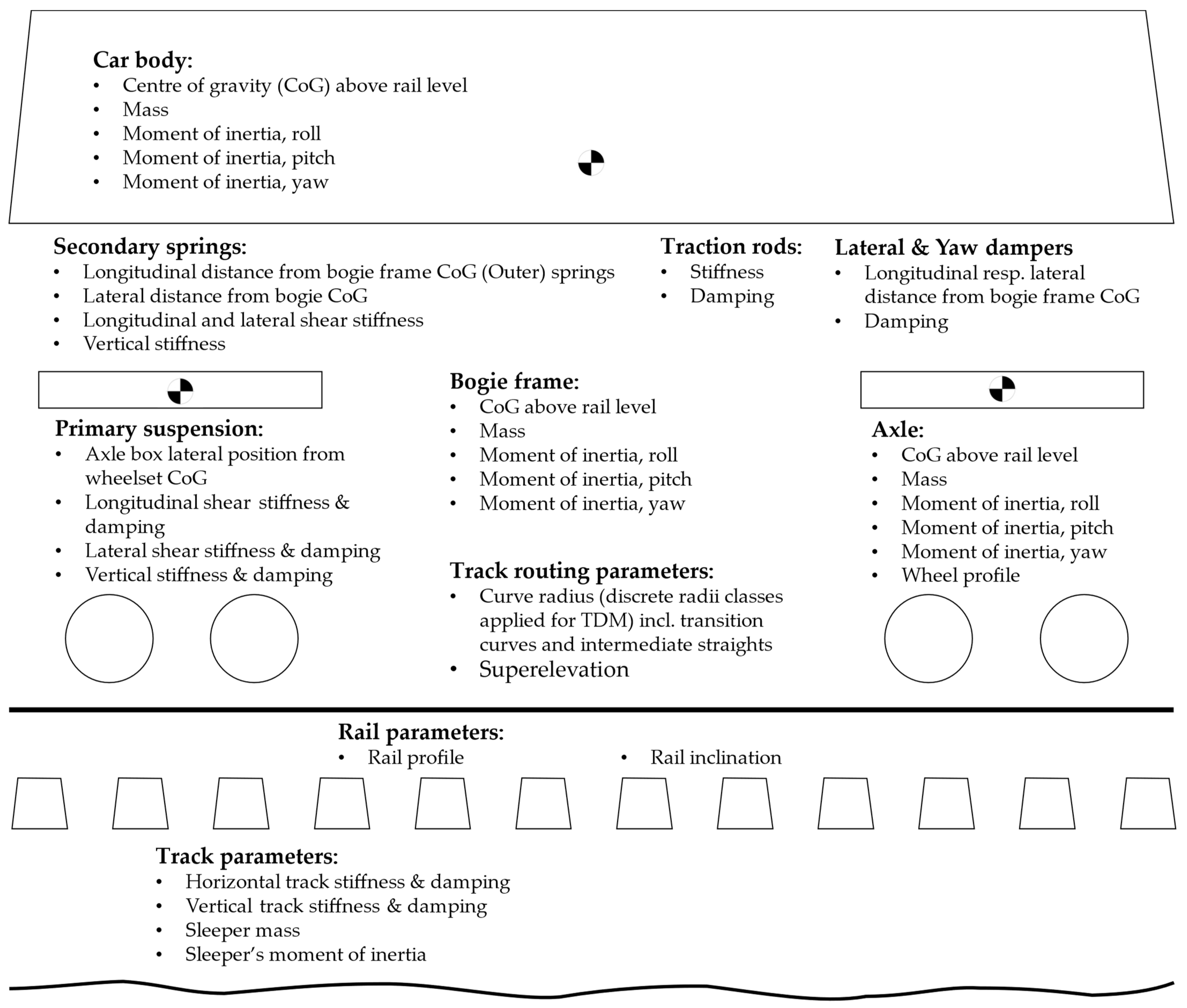
• Vehicle:

• Number of vehicles going over track sections
• Number of powered and unpowered axles per vehicle
• Speed
• Unsprung mass
• Wheel radii
• Vertical forces
• Lateral forces
• Traction power

• Infrastructure:

• Radii
• Superstructure components and their masses, damping, and stiffness parameters
• Rail surface failure (angle)
• Maintenance:
• Average maintenance actions and costs by using standard elements [3]

TDMs that include wear-inducing parameters and distinguish between boundary conditions (track radii, vehicle speed, and superstructure, etc.) describe the wear of track components in more detail compared with load by the means of tonnage and weight.

In terms of growing capacity and the necessity for system optimisation—as will be the situation for the Austrian railway network in the coming decades [4]—such TDMs have huge potential. These models can be applied as track access charging tools, as already implemented at Swiss Federal Railways (SBB) since 2017 [2]. Additionally, TDMs enable scenario analyses that allow for estimations regarding future track behaviour and maintenance effort:

• “What does a change in infrastructure components mean for the maintenance effort?”
• “What does a change in rolling stock (loco hauled vs. multiple units) mean for the maintenance effort?”
• “What does a change in the amount of trains mean for the maintenance effort?”
• “What does a change in axle load mean for the maintenance effort?”
• “What does a change in speed mean for the maintenance effort?”
• “What do irregularities in the superstructure or in rail surface (failure, insulated, or welded rail joints) mean for the maintenance effort?”

To answer such questions and perform analyses in these directions as accurately as possible, there is not only a need to understand the model approaches of each damage term, but also to realise their limitations and possibly improve them by further investigations. As the deterioration of track components is driven by multiple inherent and external influences, two main questions need to be answered for an analytic description of track component deterioration:

(A)

Which parameters have a significant impact on the associated track component?

(B)

Which of these parameters can be influenced and also described by an analytic approach?

In the following, we explain the motivation and aim of this paper, and afterwards, we discuss, analyse, and name the potential of the model’s damage terms.

3. Motivation and Aim of This Paper

The aim of this paper is to discuss and analyse the damage terms of the TUG’s TDM and their approaches. Furthermore, additional methodologies from the literature are examined. In the end, this discussion should present further potential for the TUG TDM and possible areas of investigation.

This paper focuses on a discussion of the damage terms that deal with ballast deterioration (D1), as well as rail surface wear and fatigue (D2, D3, and D4). The formula terms that represent wear of turnout elements (D5 and D6) are excluded in this paper, as well as term D7, which represents track renewal.

4. Damage Term D1—Deterioration of Ballast and the Vertical Track Geometry (Straight and Curved Lines)

The damage term D1 represents the analytical description of the vertical track geometry deterioration of ballasted tracks and, therefore, wear and settlement in the ballast bed. D1 consists of a dynamic vertical wheel force $P_2$, which is weighted by the exponent 3, as depicted in Equation (2).

This chapter briefly summarises the main tasks of the superstructure component ballast in a railway track (functions, causes, and dependencies for deterioration). Furthermore, the model’s foundations (Jenkins [5] and ORE [6]) are discussed.

4.1. Functions of Ballast in the Track System

The ballast bed, as part of the superstructure in a railway track, transfers and distributes load and high stresses at the bottom of the sleeper to a larger area of the substructure. This load distribution in the ballast bed strongly depends on the ballast characteristics themselves: the shape, surface roughness, sharp edges, and stability of the grain edges. Furthermore, the load distribution prevents subgrade from high deformation and failures. The ballast bed also provides stability and displacement resistance for the sleepers against vertical, lateral, and longitudinal forces. Due to load and track settlement, the ballast bed also enables restoring the track geometry and the required elasticity and dynamic resilience of the entire track system. Another main function of the ballast bed is to ensure drainage and prevent accumulation and vegetation [7,8].

The geometrical and physical requirements for railway ballast are prescribed by the European Standard EN 13450 [9].

4.2. Causes and Dependencies of Ballast Deterioration

The behaviour of the ballast bed concerning all the above-mentioned requirements depends on inherent characteristics, as well as external factors and the track structure [8,10].

Table 2. Causes and dependencies of ballast bed deterioration.

Inherent characteristics of ballas	Physical and mechanical particle characteristics
		Size
		Shape
		Surface roughness
		Parent rock strength
		Particle crushing strength
	Aggregate characteristics
		Particle size distribution
		Density/void ratio
		Degree of saturation
	Ballast processing
		Maintenance
External factors	Loading characteristics
		Load history
		Current state of stress
		Frequency of load
		Amplitude of vertical loads
		Load cycles
	Vehicle
		Speed
		Wheel flats
Track structure	Subsoil
	Ballast bed thickness

summarises causes and dependencies of ballast bed deterioration.

The inherent characteristics of ballast in railway tracks can be controlled by parent rock material and ballast processing (fracturing) before and after installation. In most cases, the choice of the parent rock material is driven by quality requirements, but local geologies and climate environment also affect this decision. However, hard rocks (e.g., igneous rock, such as basalt and granite) are better suited for the ballast bed in the railway track system than soft rocks (e.g., sedimentary rocks, such as limestone and dolomite). When it comes to physical and mechanical particle characteristics, hard rocks display better properties than soft rocks—therefore, parent rock is one aspect that has a significant impact on the ballast bed behaviour over time [11].

After the installation of the ballast bed, the ballast characteristics change due to ballast processing, e.g., maintenance work. The primary maintenance action employed to provide quality and durable track geometry is tamping. Tamping compacts and stabilises the ballast under the sleeper to ensure elasticity in the track system and optimise the load transfer from the sleeper to the substructure [12,13,14]. Even though tamping actions are needed for re-adjusting the target track geometry, every tamping action causes wear of the ballast grain and changes the ballast characteristics, as vibration leads to ballast friction [8,15,16]. Also, ballast stabilisation actions that restore the track’s resistance to lateral forces have an impact on the ballast grain, as horizontal vibrations are induced [17]. In the case of high ballast contamination and ballast wear, the cleaning of the ballast is performed as a maintenance operation. Ballast cleaning restores the shear strength and drainage capability of the ballast [17].

The inherent ballast characteristics that are set with the parent rock properties in a first instance (installing track) also change over the course of time due to external factors. External factors, which summarise vehicle properties, loading, and speed in this article, have a variable impact on the ballast over time. This topic is summarised in the following.

Recent laboratory tests of Gu et al. [18] show that ballast breakage significantly increases with an increase in axle load from 17 to 25 tons. Additionally, the number of tiny particles under the concrete sleepers increases dramatically with this increase in load. In addition, Stewart [19] found that high amplitudes in vertical load as a cyclic influence lead to increased vertical strain: once a level of strain is reached due to high amplitudes, this strain level is held—even if the amplitude of load (cyclic) is decreased.

Indraratna et al. [8,20] showed in laboratory tests that higher numbers of load cycles and frequency of loading lead to an increase in the permanent deformation of the ballast bed (settlement and lateral deformation). Nevertheless, Indraratna et al. [20] reported that cyclic densification of the ballast bed occurs without notable additional ballast breakage within the range from 20 Hz to 30 Hz. The majority of breakage occurs within the initial loading cycles and initial settlement after tamping.

According to Diyaljee [21] and the ORE question 117 report 5 [22], load history plays a significant role regarding plastic deformation in the ballast bed. Diyaljee’s laboratory examinations showed that the behaviour of similar samples differs if they are exposed to a variety of stress differences or if they are exposed to a single magnitude of stress. Furthermore, he investigated different load scenarios in which (a) a high load (140 kN/m²) followed by a low load (70 kN/m²) and (b) a low load followed by a high load were applied. The greatest plastic deformation occurred, in general, in the high-load phase, with deformations in the load phases with low loads being negligible. Additionally, scenario a), involving a high load followed by a low load, caused greater plastic deformation in the end. This investigation is in line with earlier findings of the ORE question 117 report 5 [22], which also showed that, within a ratio of 1 high-load amplitude to 100 low-load amplitudes (where the low load is 50% of the high load), the low load contributes less than 20% to the total settlement. High loads, therefore, lead, in any case, to greater plastic deformation.

Other external influencing factors for ballast deterioration are the vehicle properties and its operation. According to recent laboratory tests of Gu et al. [18], ballast particle acceleration and movement under the sleeper increase by over eight times within a train speed increase from 100 to 300 km/h. Time series analyses of track geometry data showed that an increase in line speed led to higher track deterioration rates [15]. Also, vehicle properties such as wheel flats not only cause a higher dynamic impact force, but also high frequent vibration, which both lead to damage to the rail surface and track structure. Bian et al. [23] investigated the amplitude of the dynamic impact force, as well as the vibration frequency, on the rail and sleeper using the finite element method (FEM). With the size of the wheel flat, the impact force on the rail and sleeper increased steadily. The rail force was more than 2.6 times higher in a 60 mm flat spot compared with a 30 mm flat spot.

Besides parent rock and external impact factors, the track structure itself also affects ballast deterioration. Kuttelwascher [7] found that hard subsoil leads to higher stress in the ballast bed, whereas soft subsoil leads to higher stress in rails due to deformation in the subsoil. Furthermore, a recent analysis by Marschnig et al. [24] showed that track segments with a 20 cm ballast bed thickness under the lower sleeper edge deteriorated faster regarding the track’s longitudinal level compared to tracks with a 30 cm ballast bed thickness. In addition, track segments with a smaller ballast bed thickness were more susceptible to singular failures.

As demonstrated in the above-mentioned findings, the degradation of the ballast bed is influenced not only by its inherent characteristics, but also by external factors. When describing ballast bed deterioration, TDMs should strive to incorporate all these influences to the fullest extent possible. However, it is important to acknowledge that TDMs have limitations, thus, the guiding principle becomes “TDM should strive for maximum accuracy while accepting the necessary level of inaccuracy”. In the subsequent discussion, we explore the model approach of D1 of the TUG TDM in greater detail.

4.3. Foundations and Adaptions of D1

The formula approach of D1 dates back to investigations in the 1980s: Jenkins [5] formulated an expression for determining the vertical dynamic wheel force $P_2$ caused by a track irregularity (rail joint) and depending on the vehicle properties. This approach excludes the occurrence of dynamic vertical forces due to rolling stock (e.g., wheel flats), but focuses on the vehicle stimulation due to rail surface irregularities. The ORE question D161.1 report 4 [6] provides the basis for the over-linear $P_2$ force approach, characterised by an exponent of 3. Equation (4) illustrates the content of the damage term D1, expressed in kN³. D1 represents a dynamic vertical wheel force subject to cubic weighting. The analytical approach for calculating the dynamic vertical wheel force $P_2$, as derived from Jenkins’ investigation, is provided in Equation (5). The coefficients $m_t$ (track mass per vehicle wheel), $c_t$ (track damping per vehicle wheel), and $K_t$ (track stiffness per vehicle wheel) are calculated as given in Equations (6)–(9).

$$D1={P_{2,s}}^3$$

(4)

$$P_{2,S}=\stackrel{static}{\overbrace{P_0}}+\stackrel{dynamic}{\overbrace{S\times 2\alpha \times \sqrt{\frac{m_u}{m_u+m_t}}\times \left(1-\frac{c_t\times \pi }{4\times \sqrt{K_t\times \left(m_u+m_t\right)}}\right)\times \sqrt{K_t\times m_u}}}$$

(5)

$$\mathrm{with}: m_t=\frac{3}{2\lambda }\left(m_r+\frac{m_s}{l}\right)$$

(6)

$$c_t=\frac{3c_s}{2\lambda l}$$

(7)

$$K_t=\frac{2k_s}{\lambda l}$$

(8)

$$\lambda ={\left(\frac{k_s}{4EIl}\right)}^{0.25}$$

(9)

$D1$	damage term 1 for ballast deterioration	N3
$P_{2,S}$	dynamic vertical wheel force (long-waved)	N
$P_0$	vehicle static wheel force	N
$S$	relevant speed (limited by vehicle or track alignment)	m/s
$2\alpha$	total joint angle	rad
$m_u$	unsprung mass per vehicle wheel	kg
$m_t$	effective vertical track mass per vehicle wheel	kg
$c_t$	effective track damping per vehicle wheel	Ns/m
$K_t$	effective track stiffness per vehicle wheel	N/m
$m_r$	rail mass per unit length	kg/m
$m_s$	mass of half a sleeper	kg
$c_s$	ballast damping per sleeper end	Ns/m
$k_s$	ballast stiffness per sleeper end	N/m
$l$	sleeper spacing	m
$\lambda$	coefficient	1/m
$EI$	rail bending stiffness	Nm2

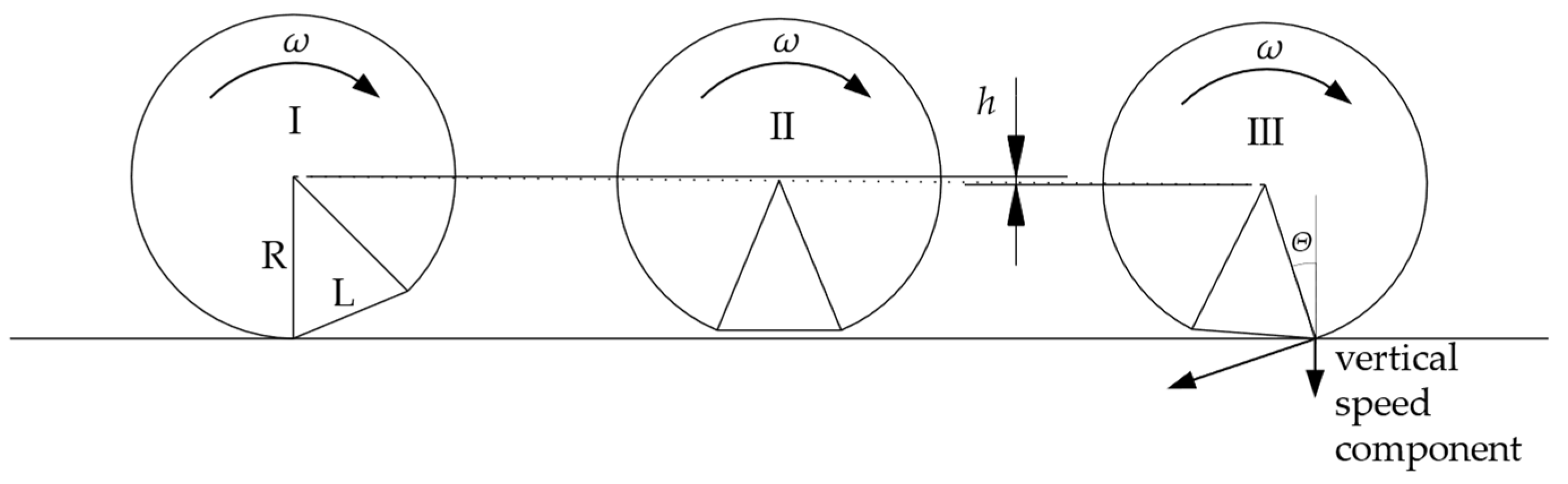
4.3.1. P₂—Dynamic Vertical Wheel Force

As early as the 1980s, Jenkins et. al. [5] emphasised that, due to imperfections in tracks and wheels, dynamic rather than static wheel forces are manifested on the track, constrained by failure criteria and maintenance economics. Track degradation, in practice, leads to a gradual increase in forces, speeding up track component deterioration until maintenance is required. Furthermore, they state that, as maintenance intervals cannot become too short, introduced forces need to be reduced and/or track deformation resistance enhanced.

As both the infrastructure but also rolling stock play significant roles in the wheel–rail interaction, investigations have been carried out in both areas since then: on vehicle development (e.g., minimising vertical forces by lightweight car bodies, bogie frames, and hollow axles [25,26,27]) and track component improvements (e.g., elastic track layers in ballasted tracks as under sleeper pads [28,29]). Jenkins’ mathematical formula methodology enables calculating vertical forces at dipped rail joints, considering vehicle as well as infrastructure parameters. This approach focuses, therefore, on vertical force occurrence due to irregularities in the infrastructure and not due to vehicle irregularities.

As depicted in Equation (5), $P_2$ consists of static ($P_{\mathit{stat}}$) and dynamic ($P_{dyn}$) force components. $P_{dyn},$ in turn, depends on six parameters that can be assigned either to the infrastructure or vehicle framework as follows:

• Infrastructure:

• Total joint angle $2\alpha$
• Effective vertical track mass per vehicle wheel $m_t$, Equation (6)
• Effective track damping per vehicle wheel $c_t$, Equation (7)
• Effective track stiffness per vehicle wheel $K_t$, Equation (8)

• Vehicle:

• Unsprung mass $m_u$
• Speed $S$

In the TUG TDM, the parameters m_u and $S$ depend on the rolling stock, track curvature, and/or transport mode ($S_{max}$ = 90 km/h for freight traffic). In contrast to the vehicle parameters, the infrastructure parameters (mentioned above) are taken as constant values. These values are equal to those proposed in the British Railway Group Standard of 1993 for their ballasted track [30]. The total joint angle $2\alpha$ is set to 0.02 rad and implies a vertical ramp discontinuity (e.g., rail joint). The effective vertical track mass m_t is set to 245 kg per vehicle wheel. According to Jenkins [5], the vertical track mass m_t implies half a sleeper and a unit length of one rail side. The effective damping $c_t$ is set to 55.4 × 10³ Ns/m per wheel and the effective track stiffness $K_t$ is set to 6.2 × 10⁷ N/m per wheel. Concerning the named parameters and Jenkins’ formula for calculating $P_2$, the Group Standard provides the following limitations for the $P_2$ force:

• The static wheel load should not exceed 125 kN or 0.13 × D (tread diameter D should not be less than 250 mm).
• A vehicle must be able to traverse a vertical ramp discontinuity in the rail top profile (e.g., dipped rail joint) on a straight track at its highest operational velocity. In this scenario, the $P_2$ force per wheel, comprising both static and dynamic components, does not exceed 322 kN.

In the Austrian federal railway network, we do not have these limitations for calculated vertical dynamic forces such as $P_2$, which are caused by discontinuities in tracks, e.g., rail surface or stiffness changes in the transition to bridges. A force limitation exists according to the European Standard 14363 [31] for static vertical forces: the maximum nominal static wheelset contact force of a vehicle must not exceed 200 kN (~20.4 tonnes of a wheelset). This includes the vehicle mass under load, however, it is a static force value for a wheelset. Dynamic forces caused by irregularities in the rail or track are, therefore, neither regulated by any force limitation (vehicle) nor by clear shape specifications/limitations of anomalies (infrastructure).

Furthermore, in Austria, rail joints have a small appearance compared with welded joints. In the Austrian railway network OeBB-Infrastruktur AG, the amount of insulated rail joints is estimated to be about 33,000 [32]. Current research activities on a few welded joints in the Austrian railway network indicate that the average total angle $2\alpha$ is far less than the value provided in the British Railway Group Standard (from about 25% to 75% of 0.02 rad). These investigations need to be expanded and also transferred to insulated rail joints to make verifiable statements.

Additionally, both the effective track stiffness $K_t$ value in the amount of 6.2 × 10⁷ N/m per wheel and the effective damping value $c_t$ of 55.4 × 10³ Ns/m per wheel are based on the infrastructure parameters of the British railway system [30]. As $K_t$ is a function of the ballast stiffness per sleeper end $k_s$, this parameter is discussed in more detail. The value for ballast stiffness $k_s$ can be estimated based on the product of the bedding modulus $C$ [N/m³] and the effective contact area between the ballast and sleeper $A_{\mathit{sleeper}}$ [m²], as shown in Equation (10). The bedding modulus number indicates the surface pressure (in N/m²), which lowers the sleeper by 1 m (or 1 cm when pressure is given in N/cm² etc.) [33].

$$k_S=C\times A_{sleeper}$$

(10)

$k_s$	stiffness per sleeper end	N/m
$C$	bedding modulus	N/m3
$A_{\mathit{sleeper}}$	effective contact area between sleeper and ballast bed	m2

Lichtberger [33] gives some guideline values for the bedding modulus $C$ in a ballasted superstructure, depending on the subsoil. According to Lichtberger, $C$ values of 2.0 × 10⁷ N/m³ indicate very poor subsoil and values of 1.5 × 10⁸ N/m³ indicate very good subsoil. Loy [34] classifies bedding modulus values of 5.0 × 10⁷ N/m³ as very soft and those of more than 4.0 × 10⁸ N/m³ as very hard and emphasises that this value strongly depends on the installation conditions, e.g., new rail lines tend to show higher stiffness values if the substructure is compacted and anti-frost-layers are installed.

Table 3. Bedding modulus $C$ and calculated ballast stiffness $k_s$ per wheel for different subsoil conditions and sleeper types.

Subsoil	$\mathit{C}$ [N/m3]	${\mathit{k}}_{\mathit{s},\mathit{concrete}}$ [N/m] ${0.5\times \mathit{A}}_{\mathit{s}\mathit{l}\mathit{e}\mathit{e}\mathit{p}\mathit{e}\mathit{r}}$ 2	${\mathit{k}}_{\mathit{s},\mathit{wood}}$ [N/m] $0.5\times {\mathit{A}}_{\mathit{s}\mathit{l}\mathit{e}\mathit{e}\mathit{p}\mathit{e}\mathit{r}}$ 3
Very poor subsoil	2.00 × 107	6.36 × 106	5.20 × 106
Poor subsoil	5.00 × 107	1.59 × 107	1.30 × 107
Good subsoil	1.00 × 108	3.18 × 107	2.60 × 107
Very good subsoil	1.50 × 108	4.77 × 107	3.90 × 107
Concrete substructure 1	3.00 × 108	9.54 × 107	7.80 × 107

¹ Tunnel or bridges, for example. ² Sleeper’s half effective supportive area of a concrete sleeper K1 (2.6 m length); $A_{\mathit{sleeper}}/2$ = 0.318 m². ³ Sleeper’s half effective supportive area of a wooden sleeper EI-1 (2.6 m length); $A_{\mathit{sleeper}}/2$ = 0.260 m².

shows the bedding modulus in a ballasted superstructure according to Lichtberger and gives some exemplary calculations for the ballast stiffness per sleeper end due to the subsoil conditions and sleeper type (concrete and wood).

With the intention of recalculating $k_s$ from the effective track stiffness $K_t$ value of 6.2 × 10⁷ N/m for the British railway system, this leads to a ballast stiffness parameter $k_{s,\mathit{British}}$ of approximately 2.3 × 10⁷ N/m. For this recalculation, a sleeper spacing $l$ of 0.7 m and a rail bending stiffness $EI$ of 6.4 × 10¹² Nm² (60 × 10¹ rail) were considered. Comparing this recalculated $k_{s,\mathit{British}}$ value of approximately 2.3 × 10⁷ N/m with the values in Table 3, rather poor subsoil might be the basis for the $K_t$ value of 6.2 × 10⁷ N/m in the British railway system. Furthermore, Lichtberger [33] states that the optimal track stiffness is somewhere between 5.0 × 10⁷ N/m and 10.0 × 10⁷ N/m according to simulations in the past.

On the basis of the analytical approach in Equation (10), the ballast stiffness per sleeper end $k_s$ can have a huge range. As $k_s$ depends on the sleeper type and subsoil conditions, these dependencies should be considered in calculating the dynamic vertical force $P_2$. In the end, this and also other infrastructure values should fit to the network the model is applied to (in average).

The effective track damping coefficient $c_t$ of 55.4 × 10³ Ns/m per wheel is a function of the ballast damping parameter $c_s$. The recalculation of c_s on the basis of $c_t$ under the same conditions, as was performed for $k_s,$ yields a value of c_s 27.5 × 10³ Ns/m. Determining ballast damping values is not that easy, however, Zhai et al. [35] used 58.8 × 10³ Ns/m as a ballast damping value in their model. This value was the result of a wheelset-dropping test in the Japanese railway system.

Giving an overview and indicative impression of the influence of each parameter on the vertical dynamic force $P_2$, some calculations are performed that are depicted in Figure 1. This figure illustrates the increase in $P_2$ due to increasing or decreasing each parameter’s initial value by 25%. As the speed $S$ and the total joint angle $2\alpha$ have a linear influence on the $P_2$ force share, $P_2$ increases by 17% compared with the reference value $P_2$. The other five depicted parameters have a non-linear influence on the $P_2$ force. The static vertical wheel force $P_0$, effective track stiffness per vehicle wheel $K_t,$ and unsprung mass m_u lead to a higher $P_2$ force of between 8 to 10%. Decreasing the effective track damping $c_t$ and track mass m_t by 25% causes increases in $P_2$ of 1 and 2%, respectively. According to the evaluations in Figure 1, not all parameters affect the vertical dynamic force $P_2$ based on Jenkins’ [5] approach to the same extent. Nevertheless, for a valid model, these parameters should ideally represent reality by using corresponding values.

4.3.2. Superlinearity—Exponent 3

Back in 1987, the Office for Research and Experiments (ORE) investigated the increase in track maintenance costs for ballasted tracks due to higher axle loads in the ORE question D161.1 report 4 [6]. Therefore, comparative measurements for 20 t and 22.5 t axle loads were performed on the railway test circuit in Velim (Czech) on the one hand. The vertical acceleration on the wood and concrete sleepers, as well as in the ballast bed, for axle loads of 20 t and 22.5 t was measured. On the other hand, the effect of a higher axle load on maintenance (costs) was analysed using three main parameters, even if other parameters (e.g., vehicle type) also have an influence:

• Traffic load $T$
• Representative dynamic wheel load $P$
• Speed $V$
• Quality index $e$
• Maintenance costs for ballasted tracks $C_m$

ORE’s investigations in the past have shown that, by using the product of “power functions”, as depicted in Equation (11), the deterioration laws of a superstructure parameter can be described on the basis of these main parameters.

$$e_{\left(Ti\right)}-e_{0\left(Ti\right)}=k_i{\times T_i}^{\alpha }\times {P_i}^{\beta }\times {S_i}^{\gamma }$$

(11)

$$\frac{C_{m,2}}{C_{m,1}}={\left(\frac{P_2}{P_1}\right)}^{\beta /\alpha }$$

(12)

$e$	quality level of a certain track quality parameter, e.g., longitudinal level
$e_{\left(T\right)}$	value for the quality level corresponding to traffic load T
$e_0$	value for the initial quality level (T = 0)
$k$	calibration factor
$T$	traffic load
$P$	dynamic vertical wheel load
$S$	speed
$C_m$	maintenance costs
$\mathsf{\alpha },\mathsf{\beta },\mathsf{\gamma }$	exponents for parameter weighting
$\mathrm{i}$	index i (1, 2) describes different traffic scenarios that lead to different cost levels C

The superstructure maintenance costs per traffic unit are proportional to the frequency of maintenance activities required to enable such traffic. These costs are inversely proportional to the maximum traffic load $T$ that can be travelled before this value is reached. This leads to Equation (12), which describes the relative change in costs as a function of the change in the dynamic vertical wheel force if the other parameters (track quality $e$, speed $S$, and traffic load $T$) stay the same. Analyses of historical data concerning track geometry have shown that the quality of the track geometry due to the traffic load $T$ can be assumed as linear ($\alpha$ = 1.00 or 0.80), whereas the quality of the track geometry due to the dynamic wheel load $P$ can be assumed to be superlinear ($\beta$ = 3.00). This leads to a $\beta$-to-$\alpha$ ratio of 3.00 (or 3.75) and provides the basis for the TUG TDM approach D1.

As this method strongly depends on track maintenance costs and the behaviour of a track segment, the ratio of $\beta$ to $\alpha$ might differ between varying track segments. The parameters of traffic load $T$, dynamic wheel load $P$, speed $S$, quality index e, and maintenance costs $C_m$ might be the main parameters, and it is expected that traffic mix (vehicle type) plays a key role.

5. Damage Term D2—Rail Surface Fatigue (Straight Lines)

The damage term D2 represents rail surface failure in straight tracks (radius > 1 km) caused by rolling stock parameters. Even the TUG TDM uses D2 for ballasted tracks, and this term is transferable to slab tracks—under the condition that the formula parameters are adapted.

This chapter explains the TUG TDM foundation of the damage term D2 concerning the approach for the dynamic vertical force and the exponent. This chapter also provides an alternative description of the dynamic force impact on the rail surface due to track irregularities. Furthermore, a suggestion for describing the force impact due to wheel flats as a vehicle property is given.

5.1. Foundations of D2 (Force and Exponent Approach)

The calculation of D2 is given in Equation (13), where the force $P_{2,}$ corresponds to Equation (5) of the damage term D1. The approach of ORE question 161.1 [6] and ORE question 141 [36] for estimating rail wear in straight track segments is similar to the exponent of 3.0 in D1, however, the costs for the rail surface are limited to fatigue damage on the rail surface, as fatigue dominates in straight tracks. Investigations of ORE [6,36] and investigations according to the former wear formula (FOT [2]) led to $\alpha$ values between 3.0 and 3.5, $\beta$ values between 3.0 and 4.5, and an average $\beta$-to-$\alpha$ ratio of 1.2.

$$D2={P_{2,s}}^{1.2}$$

(13)

D2	damage term 2 for rail surface fatigue	N1.2
$P_{2,s}$	dynamic vertical wheel force (long-waved)	N

The main idea of the damage term D2 is to describe rail surface failure in straight ballasted tracks that leads to fatigue, e.g., Squats, Head Checks, or Corrugation. The reasons for higher vertical wheel–rail forces leading to fatigue in rail surfaces can be various. Areas of discontinuity (e.g., welded or insulated rail joints or stiffness changes) in tracks cause stimulation of the rolling stock, which leads to higher dynamic forces and, consequently, to fatigue in the rail surface. Also, defects in the rolling stock (e.g., wheel flats) lead to fatigue and also plastic deformation in the rail surface. All these scenarios are irregularities that speed up rail deterioration in the context of fatigue.

5.2. Alternative Description of the Dynamic Vertical Force Impact (Caused by Infrastructure)

The $P_2$ force approach in Equation (13) is based on Jenkins’ [5] investigations. In his investigations, he describes the occurrence of vertical dynamic force peaks that are caused by insulated rail joints. He indicates the two forces, $P_1$ and $P_2$, which occur at a different amplitudes and different times after a wheel passes an insulated rail joint. $P_1$ is a high-frequency (short duration) and high-amplitude force that occurs 0.25–0.50 ms after passing the rail joint. $P_2$ is the second force peak that occurs within several ms after passing the rail joint. $P_2$ is a lower-frequency (longer duration) and lower-amplitude load.

As $P_2$ is transmitted to the track ballast and, therefore, mainly contributes to track geometry degradation, whereas the $P_1$ force peak mainly affects the rail surface, the description of rail surface fatigue in straight tracks of the damage term D2 could consist of the $P_1$ force. In Equations (14)–(17), the formula with its parameters is given according to Jenkins’ [5] model set-up. In the formula for calculating $P_1$ parameters, such as the wheel radius, the rail and sleeper mass play roles rather than track damping or track stiffness ($P_2$).

$$Iteration: P_{1,S}=\stackrel{static}{\overbrace{P_0}}+\stackrel{dynamic}{\overbrace{S\times 2\alpha \times \sqrt{\frac{K_H \times m_e}{1+\raisebox{1ex}{$m_e$}\!\left/ \!\raisebox{-1ex}{$m_u$}\right.}}}}$$

(14)

$$m_e\approx 0.4\times \left(m_r+\frac{m_s}{l}\right)$$

(15)

$$K_H=\frac{P_{1,est}-P_0}{G\times \left(P_{1,est}^{2/3}-P_0^{2/3}\right)}$$

(16)

$$G=\frac{3.86}{{R_{Wheel}}^{0.115}}\times {10}^{-8}$$

(17)

$P_{1,s}$	vehicle dynamic wheel forces	N
$P_0$	vehicle static wheel force	N
$S$	relevant speed (limited by vehicle or track alignment)	m/s
$2\alpha$	total joint angle	rad
$m_u$	unsprung mass per vehicle wheel	kg
$m_e$	effective track mass per vehicle wheel	kg
$m_r$	rail mass per unit length	kg/m
$m_s$	mass of half a sleeper	kg
$l$	sleeper spacing	m
$P_{1,est}$	estimated vertical dynamic wheel force	N
$G$	Hertzian flexibility constant (for worn tyre profiles)	m/N2/3
$R_{wheel}$	wheel radius	m
$K_H$	linearised hertzian contact stiffness per vehicle wheel	N/m

5.3. Vertical Force Impact (Caused by Vehicle)

As already mentioned before, higher vertical dynamic forces that harm the rail surface can also be induced by defective rolling stock wheels, for example, wheel flats. Bian et al. [23] examined the dynamic impact of a wheel flat on the railway track using a finite element analysis. They showed that the dynamic impact force increases monotonically with the size of the wheel flats. To evaluate their study, they used a simplified equation for calculating the wheel–rail impact force due to wheel flats. This formula is given in Equations (18)–(20) and could be another approach to representing the wheel flats of rolling stock and the force impact on the rail surface in the TDM.

$$P_{wheel-flat}=P_0\left(1+\sqrt{1+\frac{2h+\frac{{\left(\omega R\mathit{sin}\theta \right)}^2}{g}}{P_0}\times \frac{K_p{K}_b}{K_p+K_b}}\right)$$

(18)

$$\theta =arccos\left(1-\frac{h}{R}\right)$$

(19)

$$\omega \sqrt{\frac{2h}{g}}=2arcsin\left(\frac{L}{2R}\right)-arccos\left(1-\frac{h}{R}\right)$$

(20)

$P_{wheel-flat}$	vertical force per vehicle wheel due to wheel flat	N
$P_0$	vehicle static wheel force	N
$h$	dropping distance of wheelset	m
$v$	vehicle speed	m/s
$\omega$	rotation speed	1/s
$g$	gravity acceleration	m/s2
$L$	length of wheel flat	m
$R$	rolling radius	m
$ϴ$	angle	rad
$K_p$	stiffness of rail pad	N/m
$K_b$	stiffness of railroad bed incl. ballast, capping, and formation layer	N/m

As can be seen in Figure 2, the formula approach represents the vertical force impact that is induced according to the wheel flat because of a wheel drop from point I to III. In the formula approach, the static wheel force $P_0$, vehicle speed $v$, wheel radius $R$, stiffness of rail pad ${\mathrm{K}}_{\mathrm{p}}$ and ballast bed $K_b,$ and length of wheel flat $L$ represent the input parameters for the calculation.

Until now, the TUG TDM has been based on perfect rolling stock conditions. It was not the model’s core intention to represent vehicle failures. However, as such models have the potential to be used as supportive tools for scenario analyses, extending the model by another term that describes the influence of wheel flats on the rail surface could be useful.

The damage term D2 is not the only term that describes rail surface failure in straight tracks, as term D3 does so as well. The main idea of D3 is the description of rail surface wear induced by traction power. This is discussed in the following chapter.

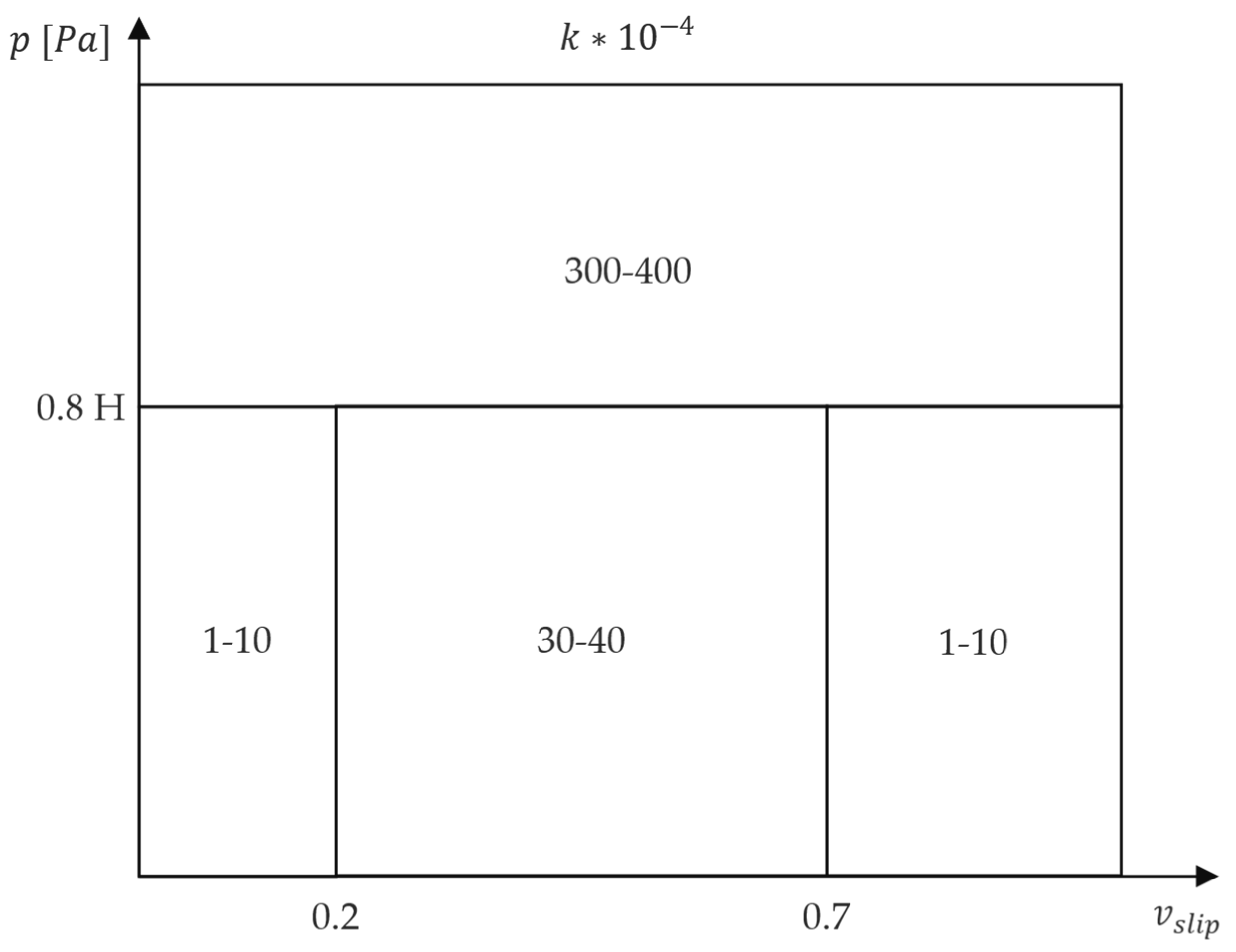
6. Damage Term D3—Rail Surface Wear (Straight Lines)

The combined effect of D3 and D2 (the latter discussed in the previous chapter) pertains to the depiction of surface damage along straight track sections. This includes fatigue-related phenomena, such as head checks, squats, and corrugation. The combined effect of these factors contributes to a comprehensive understanding of rail surface degradation and its prediction.

The damage term D3 characterises rail surface damage resulting from the influence of vehicle power. The TUG’s TDM is meant to be used for ballasted tracks, but this term is also transferable to slab tracks. The traction power value ($TPV$) is calculated by determining the power of a vehicle relative to the contact area between the rail and wheel, as Equation (21) shows. It is important to note that $TPV$ is only applicable to powered wheelsets [1].

$$D3=TPV=\frac{P_{installed}}{A_{eff}} \left[\mathrm{k}\mathrm{W}/{\mathrm{m}\mathrm{m}}^2\right]$$

(21)

TPV serves as a simple method for integrating traction into the rail degradation model. It describes the area-specific power density by using the nominal power of the vehicle and an area according to Hertzian theory [37,38]. The corresponding formula is given by Equation (22), and additional calculation factors by Equation (23).

The leading factor of $2/3$ is necessary to absorb any uncertainties.

$$A_{\mathit{eff}}=\frac{2}{3}\pi \xi \eta {\left(\frac{3 \left(1-{\nu }^2\right) }{E}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\times {\left(\frac{ P_0}{\left(\frac{1}{R_{Wheel}}+\frac{1}{R_{Rail}}\right)}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{\times 10}^6$$

(22)

$$\begin{gathered} \xi \left(\vartheta \right)=1.5281739\times {\vartheta }^{-0.8571601} \\ \eta \left(\vartheta \right)=0.4724037\times \vartheta +0.2366389 \\ \mathsf{\vartheta }=\arccos \left(\frac{R_{\mathit{Wheel}}-R_{Rail}}{R_{\mathit{Wheel}}+R_{Rail}}\right) \end{gathered}$$

(23)

The parameters required for the calculations shown above are as follows:

• Installed traction power $P_{installed}$.
• Static wheel force $P_0$.
• Material properties: modulus of elasticity $E$ and Poisson’s ratio $\nu$. It is assumed that these properties apply both to the wheel and the rail.
• Geometrical properties: radii of wheel $R_{Wheel}$ and railhead $R_{Rail}$.

According to Villwock et al. [39], Hertz’s theory has some limitations on its applicability:

• It is valid for homogeneous, isotropic material. This does not apply to the railhead due to the plastically deformed and aligned microstructure near the rail surface.
• It is conditioned on the validity of Hooke’s law. Thus, pure elastic deformation is assumed, which is not true in wheel–rail contact due to high contact pressure.
• It only considers the effect of normal stresses on the contact surface. This does not apply to the consideration of traction.
• It is valid for small deformation of both bodies in relation to body dimensions. This is true for wheel–rail contact.

Although Hertz’s theory has limitations, it can accurately calculate the contact area between the wheel and rail under a vertical load. Research [40] pointed out that Hertzian theory gives quite accurate results regarding contact area calculations compared with Kalker’s CONTACT algorithm [41]. However, for combined loads and especially their load distribution in the contact area, more complex methods (mostly numerical) are required. These methods are also necessary to determine the slip distribution in the contact surface.

7. Damage Term D4—Rail Surface Wear and Fatigue (Curved Lines)

In the context of curved tracks, where D4.1 and D4.2 are applied, three distinct types of damage can occur in ballasted as well as unballasted tracks: rolling contact fatigue (RCF), rail abrasion/plastic deformation, or a combination of both. To assess these types of damage, multi-body simulation (MBS) is used to calculate the frictional energy $T\gamma$ (T-Gamma) in the contact patch. The evaluation function, which connects contact patch frictional energy ($T\gamma$) to fatigue damage, is derived from insights provided by Burstow [42], described in more detail in Section 7.2. For application in the track deterioration model, some adaptions were performed, which are explained later in Section 7.3.

Marschnig et al. [1] provide the calculation for D4.1 in Equation (24) and for D4.2 in Equation (25).

$$\begin{array}{ll}D4.1=0& for T\gamma <15 \mathrm{N}\mathrm{m}/\mathrm{m} and T\gamma \ge 175 \mathrm{N}\mathrm{m}/\mathrm{m}\\ D4.1=n \times \left(0.02 \times T\mathsf{\gamma }-0.3\right)& for 15\le T\gamma <65 \mathrm{N}\mathrm{m}/\mathrm{m}\\ D4.1=n \times \left(\frac{-T\gamma +175}{110}\right)& for 65\le T\gamma <175 \mathrm{N}/\mathrm{m}\end{array}$$

(24)

$$\begin{array}{ll}D4.2=0& for T\gamma <65 \mathrm{N}\mathrm{m}/\mathrm{m}\\ D4.2=n \times \left(\frac{T\gamma -65}{110}\right)& for T\gamma \ge 65 \mathrm{N}\mathrm{m}/\mathrm{m}\end{array}$$

(25)

Thus, the calculation for D4 includes only the parameter $T\gamma$ as a vehicle-specific parameter and $n$ as the number of leading wheelsets of a bogie, because only these are relevant for the damage considered. However, the multi-body simulation that this is based on requires a significant number of parameters from both the infrastructure and vehicle sides. System parameters are also defined, such as the coefficient of friction. Figure 3 shows the required vehicle-related and infrastructure parameters for the MBS to calculate the wear number $T\gamma$. Further system parameters are required, for example:

• vehicle speed (to be chosen according to the curve radius, superelevation, and resulting free lateral acceleration, respectively), and
• coefficient of friction (assumption: constant coefficient of friction for whole simulation process, e.g., constant over time, location, and state of motion).

The sections below first deal with the basics—what damage looks like, what causes it, and what mechanisms are at work. Furthermore, the foundation of the model used, its adaptations for the TDM, and further investigations are presented.

7.1. Damage, Forces, and Mechanisms

The following paragraphs outline the basics of damage, forces, and stresses, as well as the underlying damage mechanisms.

Rails can suffer from visible damage, for example, surface cracks such as gauge corner cracking or head checking, as noted by Cannon et al. [43]. Furthermore, material loss leads to a reduction in cross-section and changes in profile, as noted by Lewis et al. [44]. This damage can compromise the structural integrity of the tracks and pose safety risks to train operations.

Head checks, gauge-corner cracks, and squats represent surface-initiated Rolling Contact Fatigue (RCF) defects resulting from high normal and tangential stresses between the wheel and rail. These stresses cause severe shearing of the rail’s surface layer, leading to fatigue or ductility exhaustion. Microscopic cracks propagate at a shallow angle through plastic-deformed surface layers until reaching a depth at which the steel retains its original properties. These cracks may lead to surface spalling, but in rare cases, they can turn down into the rail, posing a risk of rail breakage if undetected. The continuous formation of RCF cracks at a site increases this danger, as fractures at one crack increase the stress in the vicinity, escalating the risk of further breaks and rail disintegration. RCF initiation typically lacks a specific association with metallurgical, mechanical, or thermal faults; instead, it stems from the steel’s inability to withstand the operating conditions it faces. This issue is observed across a broad spectrum of rail-steel types commonly used today. In certain scenarios, the manifestation of this problem is evident in the formation of countless fine surface head checks on the high rail of curves, with some potentially giving rise to deep transverse head cracks. This underscores the widespread nature of RCF-related challenges in rail infrastructure. The squat defect represents another form of fatigue damage, occurring more unpredictably in very shallow curves and tangent tracks. These surface-initiated RCF issues, including head checks and squats, present particular challenges for inspection. In both cases, the development of a downward-turning fatigue crack ultimately results in rail failure. The issue can be mitigated by grinding the rail running surfaces to eliminate fatigue-damaged material.

In wheel–rail contact, both rolling and sliding occur in the contact area. On straight tracks, the wheel tread contacts the railhead, but in curves, the wheel flange may contact the gauge corner, leading to significant sliding motion. The contact area is segmented into regions of stick and others with slip occurring. Increasing the tangential load enlarges the slip region and reduces the stick region, resulting in a combined rolling and sliding contact. Once the tangential load becomes saturated, the stick region disappears, transitioning the entire contact area into a state of pure sliding. Curves, in particular, exhibit a significant sliding component, especially at the gauge corner of the railhead’s contact patch. The sliding in the wheel–rail contact, intensified by often non-existing lubrication, results in wear. This wear phenomenon exhibits a noteworthy characteristic: an escalation in the severity of loading, encompassing factors such as normal load, sliding velocity, or surface temperature, triggering a sudden change in the wear rate, marked by an abrupt increase in the volume loss per sliding distance. These jumps between the “wear regimes” are described below in the “Mechanisms” section.

Bolton et al. [45] employed an alternative method for analysing wheel–rail wear data. This method entails graphing the wear rate in grams of mass loss per metre rolled per square millimetre of contact area against $T\gamma /A$, where T represents the tractive force, γ denotes the slip, and A signifies the contact area. Through the twin disc testing of rail materials, this approach revealed three discernible wear regimes: mild, severe, and catastrophic. This method is based on an approach to friction work similar to the Burstow model.

For railway engineering, it is crucial to consider the forces that act on the rail and the resulting stresses. Grassie et al. [46] investigated the impact of traction and curving on the tangential forces between railway rails and wheels. Calculations for a two-axle bogie in curved tracks of varying radii revealed that traction significantly influences tangential forces, particularly on high rail wheels. The study observed that the ability of a bogie to steer diminishes with increased tractive effort, and low inter-axle yaw stiffness improves steering in non-powered bogies but worsens it under traction. Cant deficiency was identified as a factor that redistributes tangential loads among the four wheels, offering benefits in load distribution and reduction under various traction conditions.

According to Grassie [47], it is important to examine the tangential forces on a rail that arise from the interplay of traction and curving. These forces play a substantial role in wear and shakedown processes, providing insights into the various types of damage occurring on both rails and wheels. The study explored the rail damage associated with curves, emphasising tangential forces from curving and traction, which can alter rail shapes. High rail gauge corners align with passing wheels, while plastic flow is common in low rails. Periodic wear and plastic deformation occur due to dynamic vehicle behaviour. Reprofiling offers a solution to reducing damage and flow, especially in high rails, which is well understood and documented.

Damage mechanisms explain what happens within the rail structure under different operational conditions and stresses.

Rolling contact fatigue (RCF)

According to Kapoor et al. [48] RCF is a phenomenon that occurs in various mechanical components, such as railways, gears, and bearings, due to combined rolling and sliding contact. Cyclic loading induces crack-like flaws in the material, which can progress into larger cracks if subjected to continued loading. This can potentially result in fractures, such as rail breaks in railway systems.

In the contact patch between the wheel and rail, pressures of up to 1500 MPa and even higher can occur. Therefore, high resistance to these loads is crucial. Frequent cycles of wheel passage with high contact pressures can create crack-like flaws that subsequently evolve into small cracks. These small cracks typically grow at shallow angles, ranging between 0 and 40 degrees relative to the surface. This “crack initiation phase” is shown in Figure 4a. These cracks advance with repeated loading and may merge, as shown in Figure 4b. The branch crack can extend either upward to the rail surface or downward into the rail foot. During upward propagation, a portion of the rail surface may detach or spall, resulting in a rough surface along the rail, as shown in Figure 4c. Conversely, if the branch crack extends downward, it poses the risk of a rail break (Figure 4d), potentially leading to derailment or a severe accident.

Head checks are small surface defects that resemble hairline cracks and appear on the railhead (described and depicted in detail, for example, by Kapoor et al. [48]). These defects are typically located at the wheel–rail contact points and occur at the top of the railhead on straight tracks and in curves with gentle curvature. In sharper curves, head checks develop at the gauge corner. Gauge-corner cracking refers to the development of cracks at the corner of the rail, which are open to the surface. Transverse cracks in the rail direction have the potential to cause a rail break.

There are various models for describing the damage mechanism of RCF on the rail surface. These have different approaches and, therefore, require a different depth of the boundary conditions and input parameters, but also lead to different results. The Burstow approach ($T\gamma$ model) was chosen for the application of the TDM, as it allows for the entire life cycle to be modelled (refer to Figure 5).

On the one hand, it is possible to use highly sophisticated models like the Finite Element Method (FEM) to calculate the load and damage within a single wheel–rail contact. Therefore, detailed knowledge of the boundary conditions and parameters for simulation is required. On the other hand, there is the “Whole Life Rail Model” (Burstow’s $T\gamma$ model) for modelling rail damage across the whole life cycle of the rail. The latter is used in the TDM by TUG.

Wear

Archard’s Simple Theory of Mechanical Wear [50] and Rabinowicz’ Theory of Adhesive Wear [51,52,53,54] are two fundamental theories that provide a quantitative understanding of wear in sliding or rolling contacts.

According to Archard [50], wear is directly proportional to the product of the normal load and sliding distance, known as the Archard wear equation. This theory assumes that wear occurs due to the removal of asperities (small irregularities) from the contacting surfaces. Archard’s approach considers wear as a result of plastic deformation and material removal. The wear rate is proportional to the hardness of the softer material and inversely proportional to its elastic modulus. Archard’s model is a widely used simplification for estimating the wear in various mechanical systems. It offers a practical and accessible framework for wear analysis.

Rabinowicz’ Theory of Adhesive Wear [51,52,53,54] focuses on situations where surfaces experience adhesion due to attractive forces between atoms or molecules. Adhesive wear occurs when micro-welding and material transfer take place between the contacting surfaces. Rabinowicz proposed a critical load for adhesion, beyond which, permanent bonding occurs, leading to increased wear. This theory emphasises the role of temperature in adhesive wear and highlights the importance of effective lubrication in reducing direct metal-to-metal contact.

Both theories described above are valid for pure sliding motion. The effects of combined rolling/sliding motion on the wheel–rail contact are more complex.

The wheel–rail system is one of the most commonly used rolling pairs in rail-based transportation systems, as Sommer et al. [55] state. It is typically used without lubrication, with a few exceptions such as flange and switch lubrication. This pairing utilises the conical profile of the tread surfaces of railway wheels, which includes the transition radii to the flange, and the curved profile of railheads. These contact areas can range from being initially point-like to 100 to 200 mm², varying in size and not always maintaining an elliptical shape. The stress factors that are crucial in the context of a wheel–rail system include Hertzian pressure, tangential forces, and lateral guiding forces. The wear in this system is determined by frictional slip behaviour, which is influenced by the relative movements of the wheelset. The contact area experiences various types of friction, including adhesive, sliding, and rolling friction, which emphasise force closure.

Three wear mechanisms occur in the wheel–rail system: surface fretting, continuous wear due to slip processes, and wear influenced by adhesion and tribology. These mechanisms result in different types of wear, with rolling wear being predominant on tread surfaces and sliding wear prevailing in the flange area and corresponding rail flanks.

Jendel’s [56] wear regime models classify wear into different categories or stages, each associated with specific operating conditions and wear mechanisms. These categories may include adhesive wear, abrasive wear, fatigue wear, and others, depending on the nature of the contact and the relative motion between surfaces. As demonstrated in Figure 6, the wear coefficient experiences a sudden increase with small increments in load, whether caused by the contact load $p$ or slip $v_{slip}$.

Krause et al. [57] exposed similar findings by showing the results as wear rates of twin-disc tests at a constant slip over area-specific friction power. It is evident that wear increases significantly when the friction power surpasses a threshold value.

Due to this wear behaviour, it is essential to be able to draw conclusions about the acting wear regime when evaluating the wear. The erratic, non-linear behaviour of the relationship between the contact load and wear rate requires comprehensive knowledge of the effective wear mechanism.

Interaction of rolling contact fatigue and wear

The wear of a rail surface can be beneficial in managing cracks by removing small cracks and slowing the advancement of larger ones [58]. In Figure 7, the crack extending into a railhead is depicted. The rate of crack growth at the tip, labelled $dc$, is countered by a wear-induced reduction in the crack length at the crack mouth, labelled $dw$, during the passage of a wheel. The net crack growth, represented as $dc-dw$, reflects the combined effect of crack advancement and wear-induced reduction. The reduction in crack length due to wear depends on the angle of the crack beneath the rail surface. Cracks at shallower angles experience amplified wear rates, especially below 30°, resulting in significant reductions in crack length with each wheel passage.

When the wear rate reaches a certain level, it can decrease the net crack growth rate to zero, halting the advancement of existing cracks, or even make it negative, signifying the erosion of existing cracks. Burstow’s model demonstrates this effect as well. Figure 8 displays the individual damage functions (RCF and wear) as a function of the wear number $T\gamma$. In the damage model (refer to Figure 9), these two functions are superimposed, with wear mitigating or even reversing the damage caused by RCF [59].

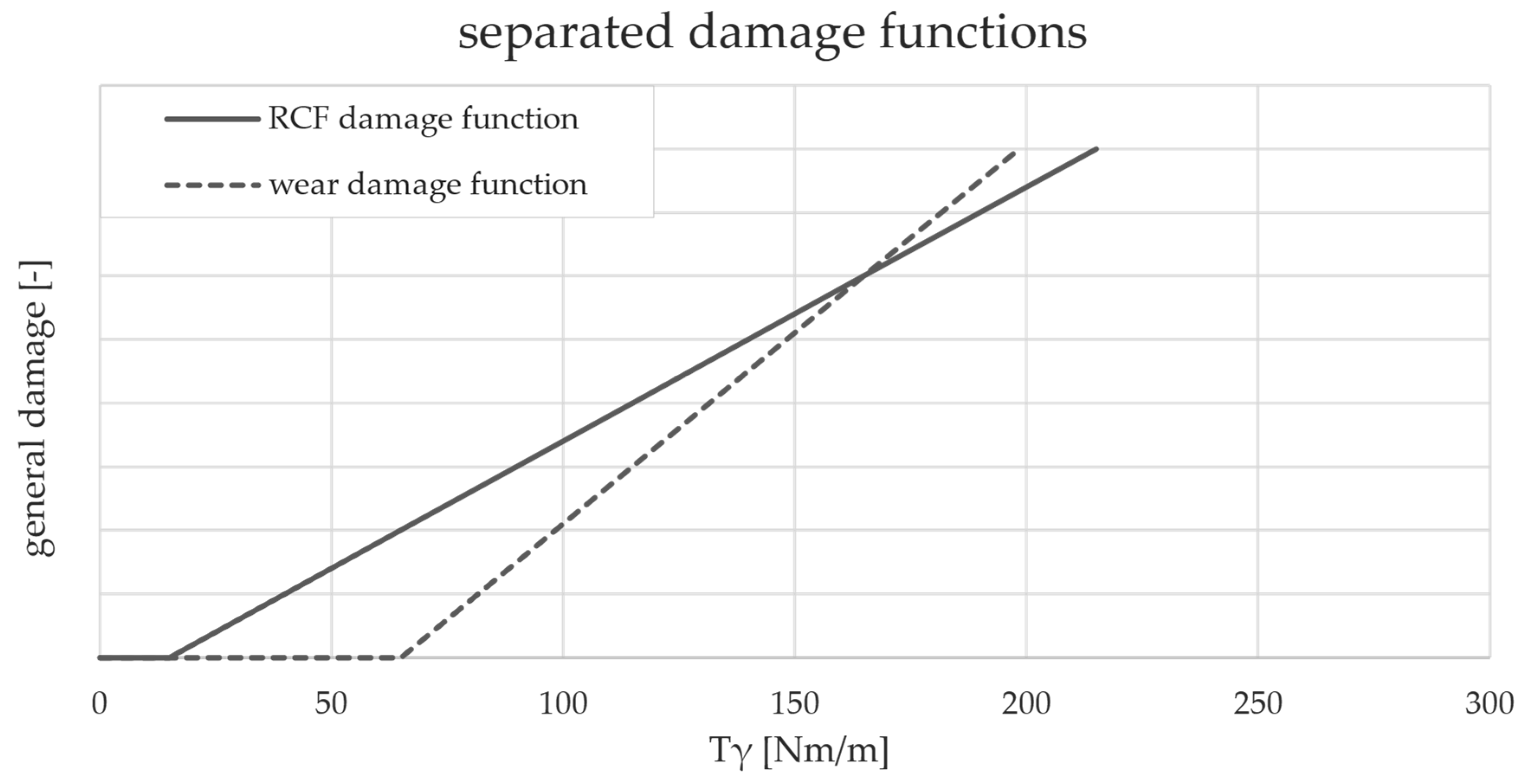
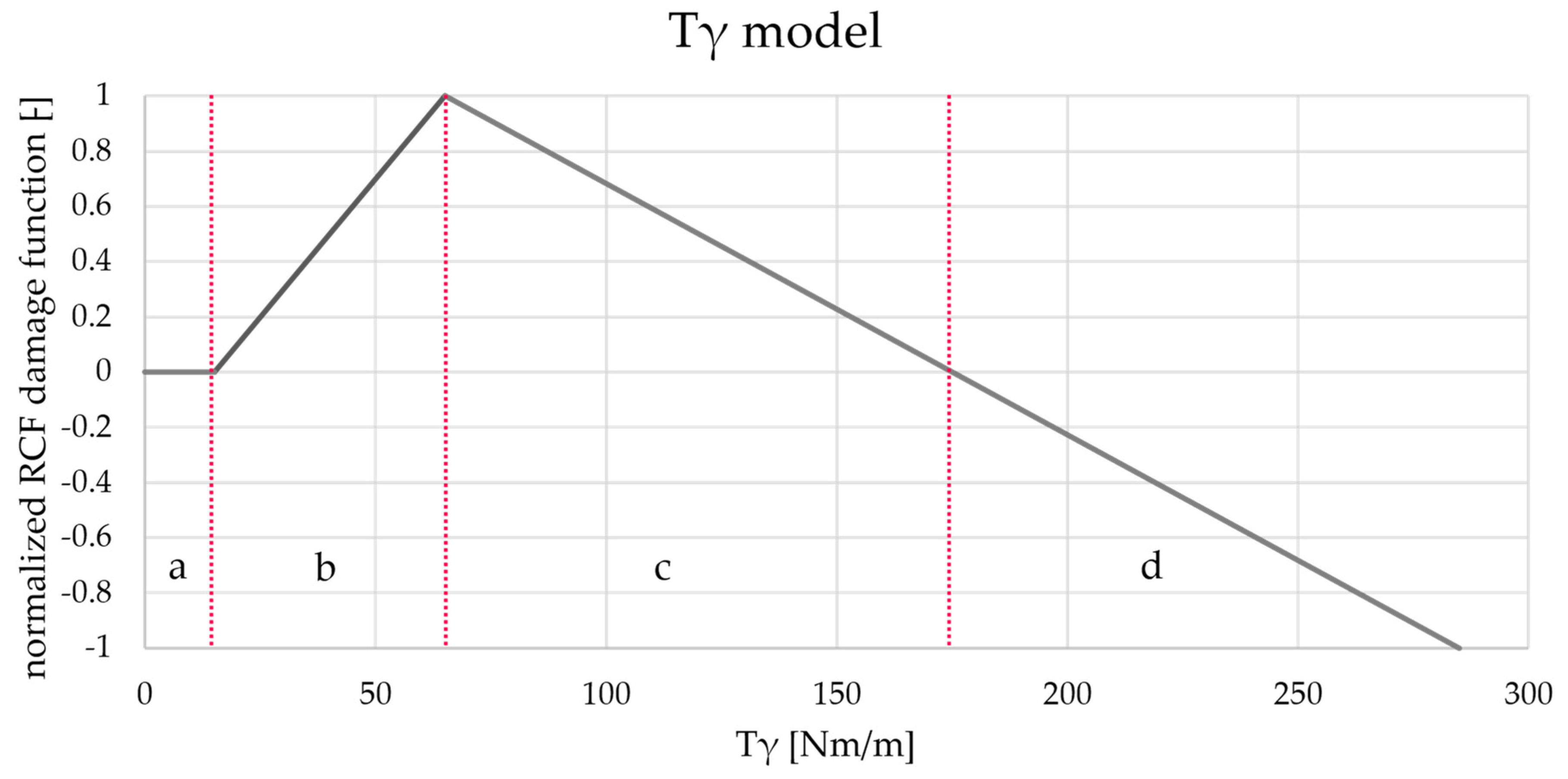
7.2. Foundations of D4—Tγ Model by Burstow

The aforementioned Burstow model [42] acts as the basis for D4 and relates the “wear number” ($T\gamma$) to RCF crack initiation fatigue damage. The wear index is calculated by summing the friction work per length of contact. This is the result of multiplying the shear force (tangential to the railhead), denoted by T, by the creep, denoted by γ, and is obtained through a multi-body simulation using vehicle dynamics software. This value is then converted into a fatigue damage index that represents the number of cycles before visible RCF cracks (approximately 2 mm in length) appear. Miner’s rule adds up the fatigue damage that results in visible RCF damage when the index limit is reached.

Burstow’s [42] definition illustrates that cracks on the rail surface grow because of the existence of crack-opening shear forces induced by traction forces on the railhead, which generate positive shear force coefficients.

The behaviour of the overall rolling contact fatigue (RCF) damage function shown in Figure 9 is influenced by individual linear damage functions for both wear and RCF (refer also to Figure 8). Below the fatigue threshold (zone a), no RCF (and no wear) occurs. As the slope increases (zone b), RCF damage develops due to plastic ratcheting. As energy dissipation increases, the wear rate increases and RCF damage is eliminated (descending slope, zone c). When the damage function becomes negative (zone d), wear completely suppresses RCF damage. Corresponding to the range boundaries are the threshold values in Equations (24) and (25).

Burstow’s function for damage caused by Rolling Contact Fatigue (RCF) [42] is linked to Miner’s rule of damage accumulation [60] in fatigue analysis. Miner’s rule is a widely used principle in fatigue studies to determine the cumulative effect of multiple loading cycles on a structure or material. The same principle is applied by Burstow for the cumulative damage of rolling contact fatigue on the rail surface due to the cyclical load of the wheel rollovers.

7.3. Burstow’s Model vs. TDM

Burstow explains that the $T\gamma$ model has been calibrated for crack initiation and its dependence on wear and is, therefore, suitable for predicting and evaluating head checks. In contrast, the TDM additionally uses the same model to evaluate wear.

For RCF assessment in the original, the decreasing range of the damage function for high-wear figures extends into a negative range (zone d—see Figure 9). This would mean that vehicles with a high $T\gamma$ reduce the overall RCF risk due to the high wear caused. This consideration was not taken into account in the TDM, as the same result is achieved by calibrating the actual maintenance costs using the fleet collective.

One limitation is that Burstow originally designed the model for rail grade R220. According to Hiensch et al. [59], the same values and characteristics also appear to be valid for naturally hard rails of grade R260 (standard rail in Austria). Nowadays, heat-treated rails of higher grades are used, especially in tight bends, for which the $T\gamma$ model must be adapted accordingly. Approaches to this are described in the Section 8.4.

7.4. Other Investigations

Bolton et al. [45] studied wear mechanisms using twin-disk tests and identified mild, severe, and catastrophic wear regimes based on wear rate, contact surface appearance, and wear debris. Burstow associated mild wear with the RCF-dominated regime and transitions to severe wear with the wear-dominated regime.

Lewis et al. [44,61] associated the mild to severe transition with the onset of full sliding contact conditions. Burstow’s RCF damage index is effective in predicting damage in locations affected by track irregularities and quasi-static curves. However, certain assumptions, such as limited wheel profiles and fixed track geometry conditions, affect the reliability of the model. Despite these limitations, the model shows good correlations between predictions and field observations of track locations with RCF.

8. Discussion and Future Potentials

8.1. D1

As evidenced by previous research, the deterioration of the ballast bed is impacted by its inherent traits (e.g., parent rock and rock processing) and track structure. These inherent traits are defined based on quality requirements, as well as local geologies. However, the properties of the parent rock and track structure further influence the behaviour of ballast bed deterioration immensely. Furthermore, ballast bed deterioration is also affected by external factors (e.g., load cycles and amplitudes, speed, and vehicle properties). At best, Track Deterioration Models (TDMs) seek to integrate the influence of inherent traits, external factors, and track structure on ballast bed deterioration.

The approach of Jenkins for describing the vertical wheel force due to jointed tracks includes many essential vehicle and infrastructure parameters. However, these parameters need to represent, on the one hand, the described infrastructure, but also the vehicle properties. As not only rail joints in the form of insulated joints occur, but welded joints also have a high incidence, the shape of these rail surface phenomena in combination with vehicle reactions due to vehicle properties (e.g., stiffnesses and damping, wheel radii, and unsprung mass) should be investigated. Furthermore, distinguishing between different superstructure conditions (e.g., rail type, sleeper type, and ballast conditions) can lead to a more precise TDM.

As the speed and total joint angle linearly influence the dynamic force part of $P_2$, these two parameters affect the total $P_2$ force most of all parameters: a 17% higher $P_2$ force by increasing either the total joint angle $2\alpha$ or speed $S$ by 25%. This linear relation between the dynamic vertical force and speed and rail surface failure needs to be investigated in more detail.

Since dynamic forces do not only occur due to track irregularities, but also due to vehicle conditions, the model could be advanced with terms that describe such impacts. For example, wheel flats cause an increased vertical impact force with the length of the wheel flat and particularly affect the rail surface. Even wheel flats are not a default case, as they do appear and not only cause rail surface failure, but also affect the ballast bed.

Parameters such as maintenance costs, traffic load, dynamic wheel load, speed, track quality, and traffic mix (vehicle types) are significant for estimating the weighting factor (exponent) of ballast deterioration according to ORE [6]. This aspect can lead to a different $\beta$-to-$\alpha$ ratio (exponent of $P_2$) between different railway networks and possibly even within a railway network. By taking historical measurement data, maintenance frequencies, and costs in consideration, it should be possible to enable a validation of the influence of the dynamic wheel force on track maintenance.

8.2. D2

The current description of rail surface fatigue in straight tracks belongs to Jenkins’ [5] $P_2$ force approach, as it is also used for the damage term D1. However, the $P_2$ force approach represents the second dynamic force peak that occurs when a wheel passes a point of discontinuity in the rail surface (e.g., an insulated rail joint). $P_2$ is, furthermore, the lower-frequency and lower-amplitude force that is transmitted to the ballast layer and the main reason for track geometry degradation. This characteristic fits to the damage term D1 rather than D2.

Better suited for the description of rail surface fatigue due to vertical force impact might be the dynamic force peak $P_1$. $P_1$ represents the high-frequency and high-amplitude force that occurs immediately (0.25–0.50 ms) after a point of discontinuity in the rail surface and affects the rail surface.

So far, the TUG TDM has been designed on the premise of ideal rolling stock conditions, with its primary focus not being to represent failures in rolling stock. Nevertheless, given the potential for such models to serve as supportive tools for scenario analyses, an expansion of the model to incorporate a term describing the impact of wheel flats on the rail surface could prove beneficial. Therefore, the equations of Bian et al. [23] offer an alternative approach to modelling wheel flats in rolling stock and to assessing their impact on the rail surface within the framework of the TDM.

Concluding the description of rail surface fatigue, it should be mentioned here that the interactions of damage mechanisms in the railway system are not covered in this TDM. Even though it has already been shown, e.g., by Loidolt et al. [62], that spots of discontinuity on the rail surface lead to a worse track quality (up to 50% worse on average), the interaction between damage mechanisms is very challenging for TDM.

8.3. D3

The current TPV approach is a simple method for including traction in damage assessment. However, there is potential for further development to consider the specific traction applied in greater detail, particularly in relation to rail surface damage. Possible expansion steps are listed in the following.

A step towards further development could be to consider traction slippage. By considering the stable (rising) range of the traction–slip curve, the utilisation of the friction coefficient can be included in the evaluation. This means that, in addition to the surface-specific power, the (micro-)slip generated at the wheel–rail contact is also used for damage assessment. This makes it necessary to define a fixed traction–creepage curve. Magel [63], for example, has conducted studies in this area. Further exploration could involve examining the unstable (falling) segment of the friction–slip curve, e.g., the area of higher slip. This includes the effect of temperature input into the rail surface. This requires extensive knowledge of the vehicle-specific slip behaviour (slip control) and the actual behaviour of the coefficient of friction.

Several approaches can be considered for further development:

• Integrating traction into the $T\gamma$ model and applying it to both straight and curved tracks could improve the assessment of rail damage.
• Investigations of alternative models that incorporate traction to assess rolling contact fatigue (RCF) and wear, such as those proposed by Six et al. [64], may offer improvements in combined damage assessment.
• Extending Hertzian theory to include rail deflection is an open research topic and offers a promising avenue for advancing the theoretical framework.
• Investigations of the influence of weather conditions, particularly the effect of water on adhesion levels, as emphasised by Buckley-Johnstone et al. [65], could provide valuable improvements in the assumption of friction coefficients and their behaviour.

8.4. D4 in General

There are several ways to develop the D4 damage term, for which in-depth research is required. In general, the $T\gamma$ model used should be adapted to the higher rail steel grades used today compared with the past. It is, therefore, necessary to adjust the formula accordingly. The basis for this is provided by empirical data. There have been attempts to adapt to higher rail grades, see Burstow [66] and Hiensch et al. [59], but there is not yet a complete model. For proper results, more empirical data and their evaluation are necessary.

As mentioned above, investigating alternative combined damage assessment models [64] that include traction may be a way to assess more aspects of rail damage in one model. This would have the advantage that the same damage model could be used, regardless of the wheelset type (driven or free rolling) and the alignment (straight or curved). Nevertheless, all operating cases (rolling, driving, and braking) could be mapped.

In the European Standard EN 14363 [31], a method to approximate $T\gamma$ is described. This procedure is based on measured values collected during a registration test drive and, therefore, can only be used without simulation for registered (and, therefore, already existing) vehicles [67].

A damage term for short pitch corrugation (e.g., D4.3) could be included in order to map a part of the rail surface damage that has not been considered yet. This damage phenomenon occurs on the inner rail of medium to sharp curves and requires maintenance (grinding) if it becomes too intense. Therefore, in terms of damage assessment, the complete mapping of all occurring damage mechanisms is necessary.

As mentioned in the previous section, weather conditions have a major influence on the water or moisture in the wheel–rail contact. Not only is the coefficient of friction (and its behaviour) affected, but also crack propagation. Water penetration up to the crack tip has a crack-opening effect when a wheel is rolled over it and can significantly accelerate the crack growth rate. Variation in the coefficient of friction due to water or other media as an intermediate layer can cause a significant change in the micro-slip in the contact area. This, in turn, has a significant effect on the wear number $T\gamma$ [68].

8.4.1. D4.1—RCF Assessment

The $T\gamma$ model developed by Burstow is an established method for obtaining reliable results for the assessment (or prediction) of RCF-related damage. This is particularly true for crack initiation and growth. By adapting the wheel and rail profiles used for simulation, away from design profiles which are currently assumed and towards real wear profiles, more realistic results can be obtained. There is certainly a need for research in this area.

Currently, the coefficient of friction is assumed to be constant (both temporally and spatially in contact) for the application of the TDM. The Swiss Federal Office of Transport (FOT) [2] specifies 0.3 as the coefficient of friction for vehicle dynamics simulations. However, it is known that the actual friction conditions have a significant influence on the wear number [69]. Further research in this area could extend the model to account for non-constant friction coefficients.

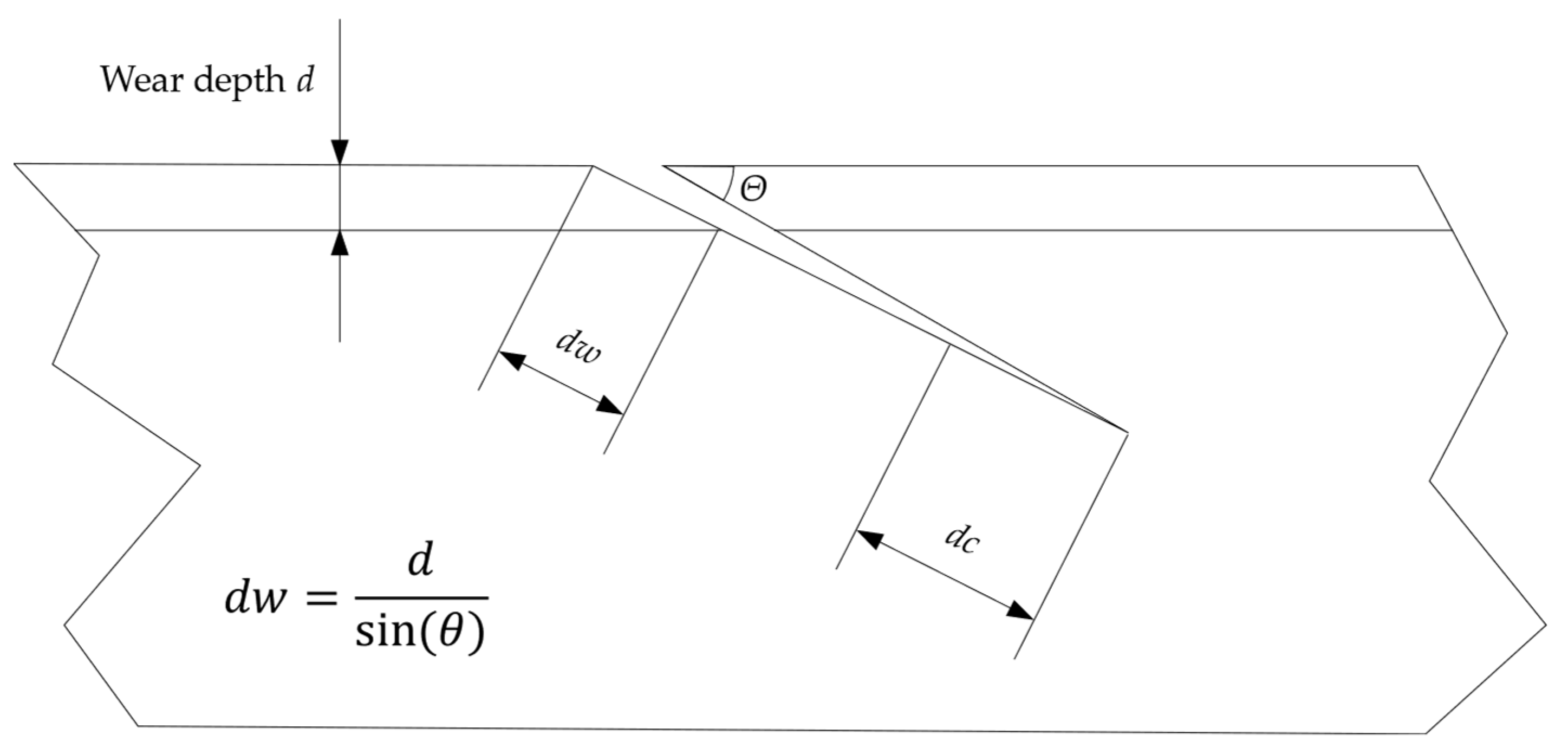
8.4.2. D4.2—Wear Assessment

Currently, the TDM uses the same model, e.g., the same parameters, for wear evaluation as RCF. As described above, the $T\gamma$ model was not originally developed for the sole purpose of modelling wear. Due to the strong interaction between the two types of damage (superposition), in principle, they cannot be separated and must always be considered together. However, it could be useful to use other relevant parameters (especially vehicle parameters) for wear. Other influences on rail wear are obviously not yet known and are, therefore, not considered in the wear model.

Understanding wear in railway infrastructure is a complex topic that involves considering numerous boundary conditions. The influences of all these conditions (see Figure 10) are not fully known, with some factors remaining completely unknown. Ongoing research aims to shed light on these aspects. The parameters influencing wear can be broadly categorised into three main groups: vehicle parameters, infrastructure parameters, and operating parameters. Each of these factors contributes to the level of wear experienced by railway tracks and their associated components.

On the vehicle side, wear is primarily caused by horizontal guiding forces and tangential forces in conjunction with their respective slips. However, to investigate individual influences on wear, it is necessary to consider all other factors. This opens up a broad field for future research on rail wear. To properly evaluate these impacts, it is crucial to separate them from one another, so that each influence can be considered separately.

8.5. Further Scope of Application

Even if the track deterioration model has only been applied for ballasted tracks so far and the infrastructure parameter discussion was about ballasted tracks in this paper, we want to emphasise that the model’s damage terms from D1 to D6 are transferrable to slab tracks too. When conducting this, of course, the infrastructure parameter values need to be adapted for slab tracks. Furthermore, the relevance of each damage term will be different between ballasted and unballasted tracks due to different maintenance actions, costs, and frequencies. For example, when assessing ballasted tracks, D1 is the most relevant damage term because of the ballast bed maintenance frequency and costs. Ballast bed maintenance is comparable costlier, but does not exist in slab tracks. In slab tracks, elastic layers need to be replaced instead, being less costly compared to ballast maintenance.

The only term that is not transferrable to slab tracks is damage term D7, as D7 represents track renewal. Track renewal and track service life in ballasted tracks are strongly driven by track components (e.g., sleeper type and parent rock material, etc.), loading, and radii. This relation does not apply for slab tracks in this form.

Summing up, even though there are some differences in the application of the model, the model methodology and damage terms from D1 to D6 also work for slab tracks.

9. Conclusions

The examination of damage terms D1, D2, D3, and D4 underscores the efficacy of the Track Deterioration Model (TDM). Nevertheless, despite its notable performance, the model still shows areas with potential for enhancement.

Belonging to the damage term D1, the approach of the dynamic vertical force impact $P_2$ integrates numerous critical parameters related to both vehicle and infrastructure aspects. These critical parameters should be adjusted. For example, the total joint angle seems to be overestimated for the Austrian track network in the case of welded joints. Furthermore, track parameters such as stiffness values and track mass vary within the network according to different substructure conditions and superstructure components. Adjusting these parameters, on the one hand, requires studying the current track situation in the Austrian railway network (joint angles, frequency, and shape of rail surface effects, stiffnesses, and subsoil conditions, etc.). On the other hand, a cross-check with track measurement data has to be carried out to calibrate the model approach with reality.

Regarding the damage term D2, the description of rail surface fatigue in straight tracks, further exploration is worthwhile to assess the suitability of utilising $P_1$ instead of $P_2$ for describing rail surface damage. Furthermore, one aim could be to extend the model with exogenous impact forces due to rolling stock failures (wheel flats).

Further research on rail surface fatigue and wear—covered by the damage terms D3 and D4—will lead to a better understanding of the relationships between “load on the rail” and “damage to the rail”. On the one hand, the influence of the traction energy input itself will be analysed in more detail and, on the other hand, vehicle-describing parameters will be investigated. Taken together, the damage terms D3, D4.1, and D4.2 will be analysed for their validity or further developed and adapted to current standards.

By analysing empirical data, e.g., track measurement data, and comparing them with vehicle collectives to be studied in detail, it will be possible to draw conclusions about the effect of the individual vehicle (or vehicle axle) on the track. By including an analysis of the track surface signal, short-wave effects such as short pitch corrugation could also be considered and formulated as a further damage term in the TDM (e.g., D4.3).