Buckling Instability of Monopiles in Liquefied Soil via Structural Reliability Assessment Framework
Abstract
:1. Introduction
1.1. Overview
1.2. The Aftermath Impact of Earthquakes on a Transport Network
2. Literature Review
Text Structure
3. Methodology
3.1. Mathematical Formulation Framework
3.2. Critical Pile Length Formulation
3.3. Unsupported Pile Length Formulation
3.4. Limit State Function Formulation Using the Hasofer–Lind Reliability Index
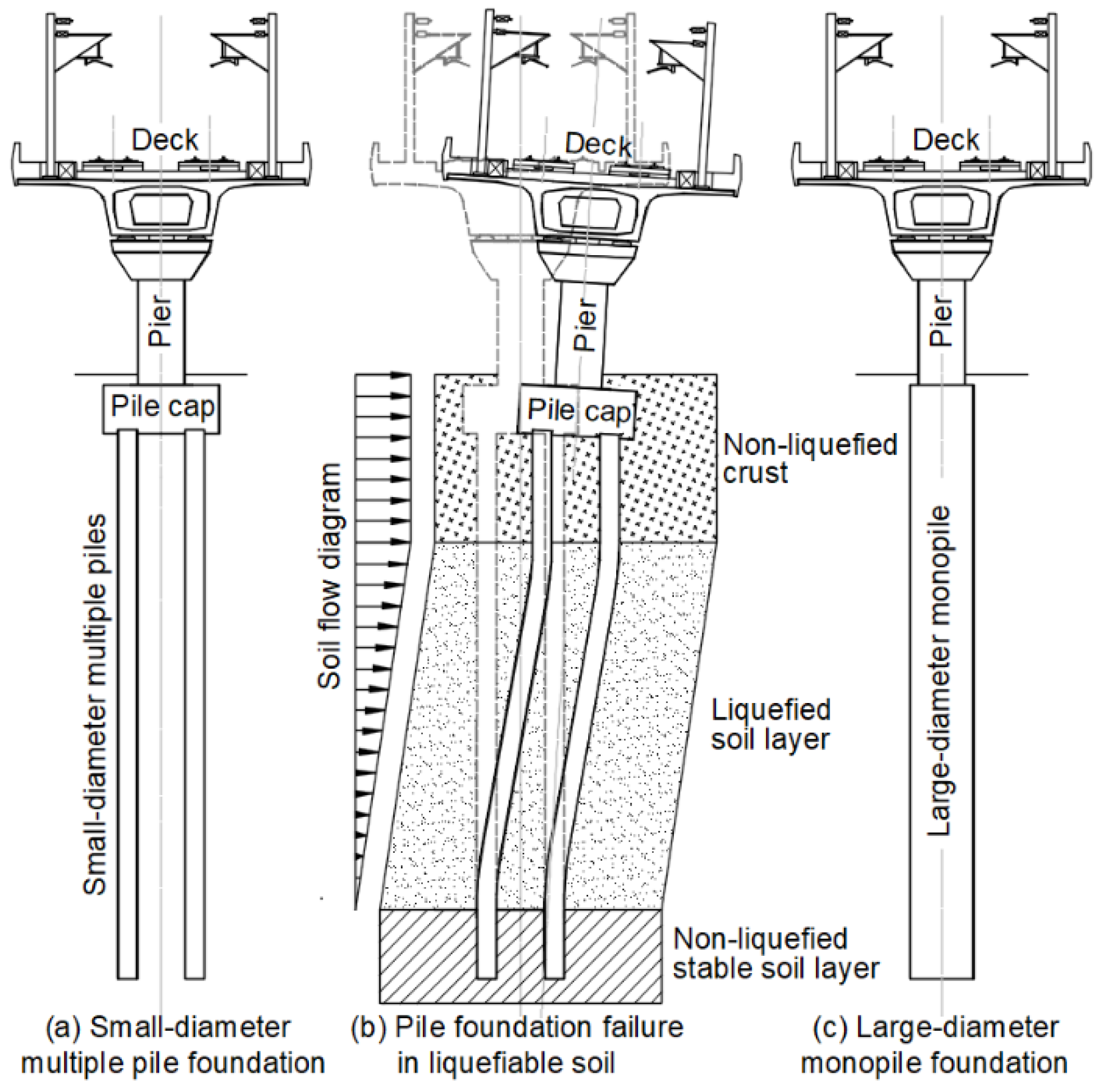
4. Case Study
5. Results and Discussion
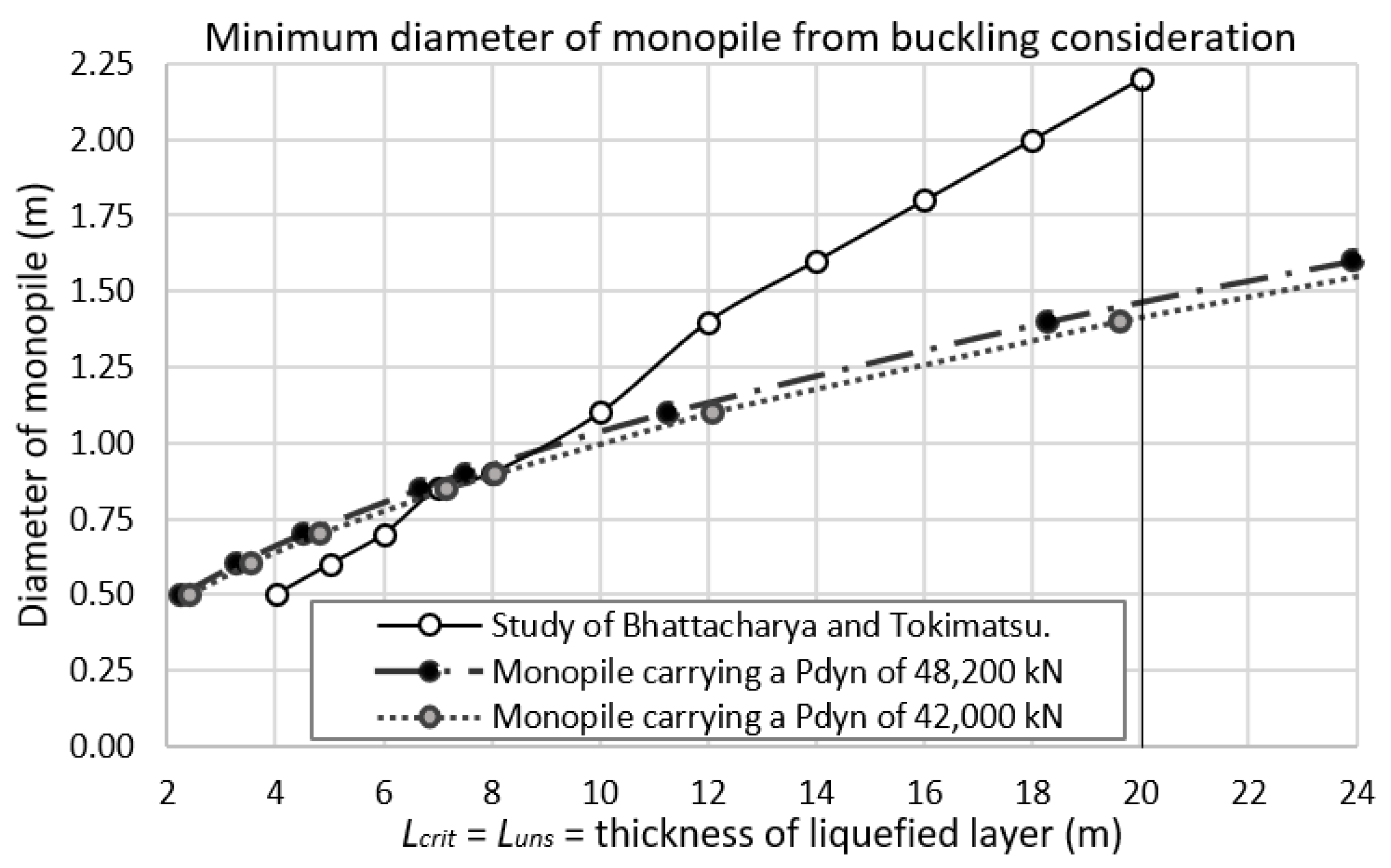
5.1. Current Study Validation
5.2. Current Study’s Pile Length Comparison
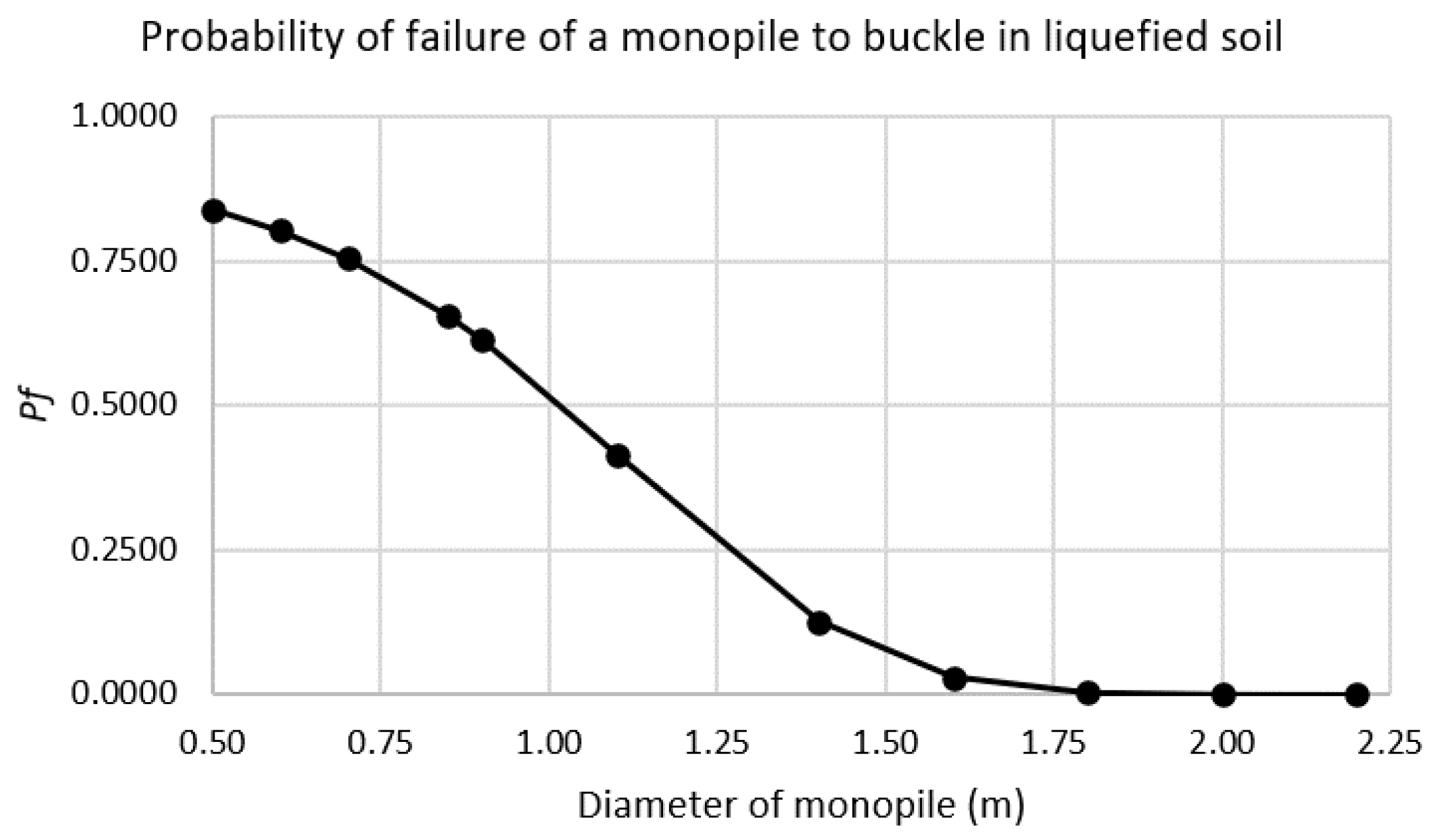
5.3. Current Study’s Probability of Failure Analysis
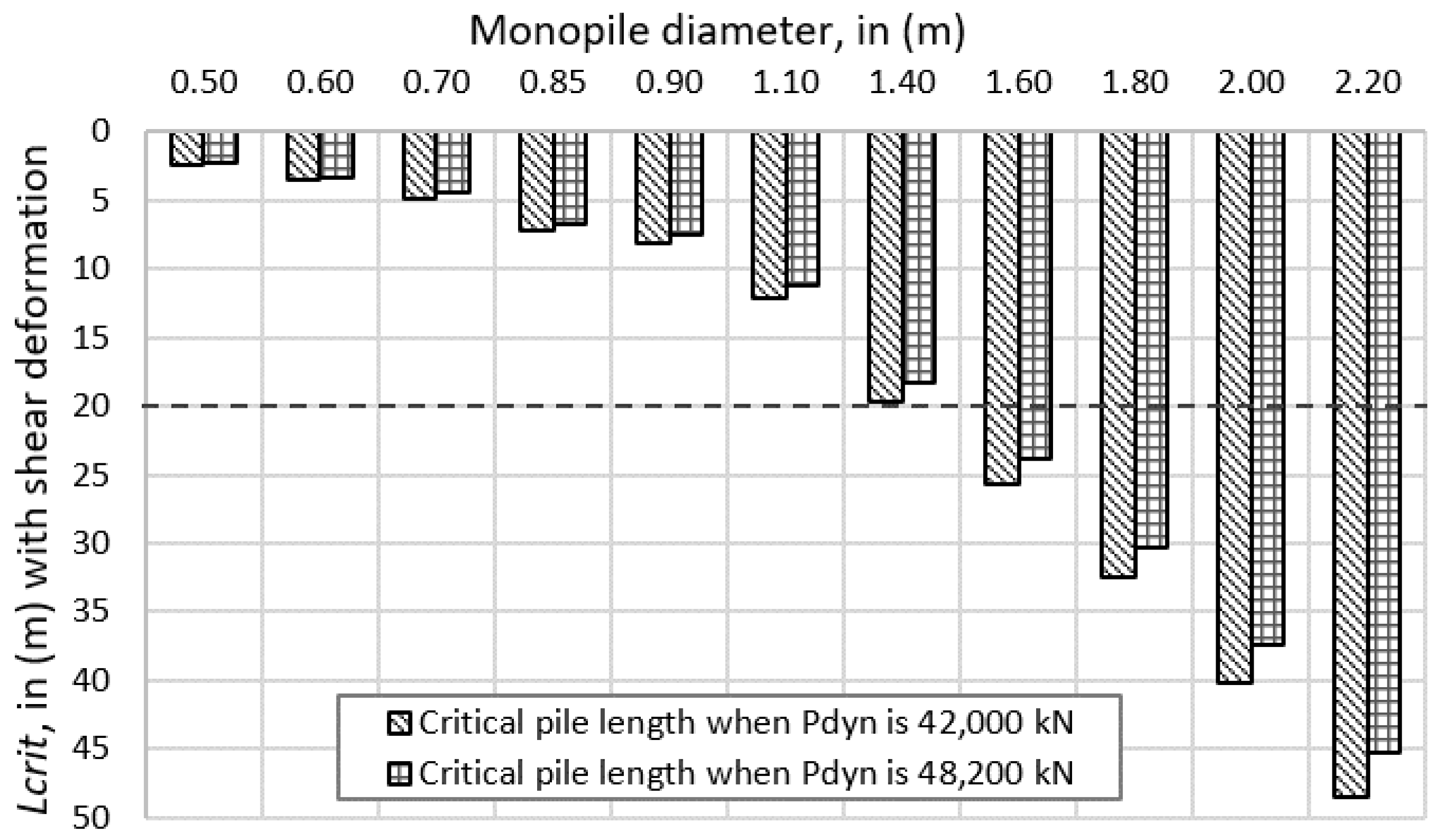
5.4. Current Study’s Shear Deformation Effect Analysis
6. Conclusions
- The validation using the study of Bhattacharya and Tokimatsu [40] showed good agreement for 0.85–0.90 m monopile diameters, where the condition of Lcrit = Luns occurred at 6.69–8.05 m depths from the ground level. However, with a smaller diameter than 0.85 m, the estimated Lcrit = Luns condition was at lesser depths, while for a larger diameter than 0.90 m, the estimated Lcrit = Luns condition was at deeper depths.
- The increase in Pdyn significantly affected the large-diameter monopiles because the movement of Lcrit required a longer range than the monopiles with smaller diameters.
- Buckling will likely occur in monopiles with diameters of 0.5–1.60 m in fully liquefied soil because the Pf value is nearly one. On the other hand, buckling will likely not happen in monopiles with diameters of 1.80–2.20 m because the Pf value is zero. Hence, the reliable monopile diameter was 1.80 m for the current study’s HSR bridge model.
- The current study also analyzed the effect of shear deformation on large-diameter monopiles. The difference in the analysis outcome was 0.30% of Lcrit, indicating that shear deformation has less of an effect on large-diameter monopile buckling.
- The transformed coordinate system, illustrated in Figure 4b, by Hasofer and Lind can be further developed to visually indicate the limit state surface because it is an isosceles triangle representation. If the perpendicular distance from the longest side of the triangle to the (0,0) origin is farther, then this might indicate a lower likelihood of failure. However, if the perpendicular distance from the longest side of the triangle to the origin is too close, then this might indicate a greater likelihood of failure.
- Treating the monopile as a beam element might oversimplify the structural reliability assessment and neglect important considerations related to the monopile’s axial response. The technical reason for this is that beam element analysis typically involves studying bending moments, shear forces, and deflections, which may not be as relevant in liquefied soil conditions, where the primary concern is often the monopile’s axial capacity to support vertical loadings without buckling instability.
- The monopile may fail due to combined failure mechanisms, such as buckling, bending, and torsion, in which axial compression, lateral deformation, and rotational loading act simultaneously on the pile during the transient stage, a short period from the phase with no soil liquefaction to the fully liquefied soil phase [55].
- The research considered a pile fixity depth (Dfix) sufficiently anchored on hard strata to secure the pile bottom while considering no settlement and overturning. The complex behavior of liquefied soil is challenging to model accurately, and it can vary depending on factors such as the soil type, density, and initial conditions.
- The HSR bridge model assumed a fully fixed rigid connection between the pier column and monopile foundation, in which the pier column remained elastic during earthquake shaking. The fixed connection means that the two elements (the bridge pier and monopile) did not rotate or move relative to each other.
- The current study did not consider the transient stage of liquefaction. During a short period from no soil liquefaction to fully liquefied soil, the monopile experiences a range of loading conditions. The dynamics of soil liquefaction may significantly impact the pile’s behavior and resistance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Description |
|---|---|
| A | Cross-sectional area |
| d | Minimum pile diameter |
| Dfix | Pile fixity depth or additional length for anchor the pile in hard strata |
| E | Elastic modulus |
| FS | Factor of safety |
| Fz | Severity function |
| I | Moment of inertia |
| G | Shear modulus |
| g(x) | Limit state function and the basis in assessing reliability |
| g(y) | Transformed limit state function |
| K | Column’s effective length factor |
| L | Unsupported column length |
| Lcrit | Critical pile length and the capacity for reliability assessment |
| Luns | Unsupported pile length and the demand for reliability assessment |
| LPI | Liquefaction potential index |
| M | Bending moment |
| N | Numerical factor |
| P | Axial force |
| Pstat | Static axial load |
| Pdyn | Dynamic axial load |
| Pcr | Critical axial load |
| Pcr+s | Critical axial load with the effect of shear deformation |
| Pe | Euler’s buckling |
| Pfail | Monopile’s actual failure axial load due to buckling instability |
| PL | Probability of liquefaction |
| PG | Probability of ground failure |
| Pf | Probability of failure of a monopile in liquefied soil conditions |
| Q | Shearing force |
| Soilliquid | Liquefied soil profile |
| Soilhard | Non-liquefied hard strata |
| w(z) | Weighting factor |
| Z | Liquefiable soil depth, which should not exceed 20 m |
| α | Dynamic amplification factor |
| β | Reliability index |
| δ − x | Displacement at any cross-section a-b within the column element |
| Reduction factor | |
| μ | Mean |
| σ | Standard deviations |
| Φ (.) | Standard normal distribution’s cumulative distribution function |
| ν | Poisson’s ratio |
References
- Bachinilla, B.; Evangelista, A.; Siddhpura, M.; Haddad, A.N.; da Costa, B.B.F. High-Speed Railway Bridge and Pile Foundation: A Review. Infrastructures 2022, 7, 154. [Google Scholar] [CrossRef]
- Mallick, M.; Mandal, K.K.; Sahu, R.B. A Case Study of Liquefaction-Induced Damage to a Port Building Supported on Pile Foundation. In Dynamics of Soil and Modelling of Geotechnical Problems; Satyanarayana Reddy, C.N.V., Krishna, A.M., Satyam, N., Eds.; Springer: Singapore, 2022; pp. 319–330. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice-Hall Civil Engineering and Engineering Mechanics Series; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Wang, C.-Y.; Manga, M. Liquefaction. In Water and Earthquakes; Wang, C.-Y., Manga, M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 301–321. [Google Scholar]
- Cubrinovski, M.; Ntritsos, N. 8th Ishihara lecture: Holistic evaluation of liquefaction response. Soil Dyn. Earthq. Eng. 2023, 168, 107777. [Google Scholar] [CrossRef]
- Selcukhan, O.; Ekinci, A. Assessment of Liquefaction Hazard and Mapping Based on Standard Penetration Tests in the Long Beach and Tuzla Regions of Cyprus. Infrastructures 2023, 8, 99. [Google Scholar] [CrossRef]
- Taftsoglou, M.; Valkaniotis, S.; Karantanellis, S.; Goula, E.; Papathanassiou, G. Preliminary Mapping of Liquefaction Phenomena Triggered by the February 6, 2023, M7.7 Earthquake, Türkiye/Syria, based on Remote Sensing. Zenodo 2023. [Google Scholar] [CrossRef]
- Dal Zilio, L.; Ampuero, J.-P. Earthquake doublet in Turkey and Syria. Commun. Earth Environ. 2023, 4, 71. [Google Scholar] [CrossRef]
- Liu-Zeng, J.; Wang, P.; Zhang, Z.; Li, Z.; Cao, Z.; Zhang, J.; Yuan, X.; Wang, W.; Xing, X. Liquefaction in western Sichuan Basin during the 2008 Mw 7.9 Wenchuan earthquake, China. Tectonophysics 2017, 694, 214–238. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, X.; Mou, T.; Liu, Z. Analysis of the Prevention Measures for Earthquake Damage and Flood Disasters of Bridges in Mountainous Areas of Sichuan. J. Phys. Conf. Ser. 2020, 1624, 042042. [Google Scholar] [CrossRef]
- Finn, W.D.; Fujita, N. Piles in liquefiable soils: Seismic analysis and design issues. Soil Dyn. Earthq. Eng. 2002, 22, 731–742. [Google Scholar] [CrossRef]
- Madabhushi, G.; Knappett, J.; Haigh, S. Design of Pile-Foundations in Liquefiable Soils; Imperial College Press: London, UK, 2010. [Google Scholar]
- Hsu, J.T.; Aila, W.; Chang, C.H. Monopile design applied in the Panama metro line 2. In Proceedings of the 16th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, ARC 2019, Taipei, Taiwan, 14–18 October 2019; Volume 2, pp. 2–4. Available online: https://yo-1.ct.ntust.edu.tw:8887/tgssp/file/16ARC/file/YGES-003_YGES15.pdf (accessed on 13 March 2022).
- Gauthier, Y.; Montens, S.; Paineau, T.; Arnaud, P. Dubai metro challenge for a fast track construction. In Tailor Made Concrete Structures; CRC Press—Taylor and Francis Group: Boca Raton, FL, USA, 2008; pp. 982–997. [Google Scholar]
- Empelmann, M.; Whittaker, D.; Los, E.; Dorgarten, H.-W. Taiwan High-Speed Rail Project—Seismic Design of Bridges across the Tuntzuchiao Active Fault. In Proceedings of the 13th World Conference on Earthquake, Vancouver, BC, Canada, 1–6 August 2004; pp. 1–14. Available online: https://www.iitk.ac.in/nicee/wcee/thirteenth_conf_Canada/ (accessed on 12 August 2023).
- Adak, G.; Bhattacharya, G.; Bhattacharya, S. Failure Mechanisms of Piles in Liquefiable Soils. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; IOS Press: Amsterdam, The Netherlands, 2009; Volume 1–4, pp. 1177–1180. [Google Scholar] [CrossRef]
- Fardis, M.; Carvalho, E.; Elnashai, A.; Faccioli, E.; Pinto, P.; Plumier, A.; Gulvanessian, H. Designers’ Guide to EN 1998-1 and 1998-5. Eurocode 8: Design Provisions for Earthquake Resistant Structures; Thomas Telford Ltd.: London, UK, 2005. [Google Scholar]
- JRA. “Specifications for Highway Bridges, Part 5, Seismic Design”. Japanese Road Association. 2012, p. 402. Available online: https://www.road.or.jp/english/publication/index.html (accessed on 12 August 2023).
- NEHRP. NEHRP Recommended Seismic Provisions for New Buildings and Other Structures (FEMA P-2082-1). Vol. 1 and 2. Federal Emergency Management Agency (FEMA), 25 February 2020. Available online: https://www.fema.gov/node/nehrp-recommended-seismic-provisions-new-buildings-and-other-structures (accessed on 12 August 2023).
- Adhikari, S.; Bhattacharya, S. Dynamic Instability of Pile-Supported Structures in Liquefiable Soils during Earthquakes. Shock Vib. 2008, 15, 665–685. [Google Scholar] [CrossRef]
- Rostami, R.; Mickovski, S.B.; Hytiris, N.; Bhattacharya, S. The Dynamic Behaviour of Pile Foundations in Seismically Liquefiable Soils: Failure Mechanisms, Analysis, Re-Qualification. In Earthquakes—From Tectonics to Buildings; Salazar, W., Ed.; IntechOpen: Rijeka, Croatia, 2021; p. 32, Chapter 8. [Google Scholar]
- Mohanty, P.; Xu, D.; Biswal, S.; Bhattacharya, S. A shake table investigation of dynamic behavior of pile supported bridges in liquefiable soil deposits. Earthq. Eng. Eng. Vib. 2021, 20, 1–24. [Google Scholar] [CrossRef]
- Mokhtar, A.-S.A.; Abdel-Motaal, M.A.; Wahidy, M.M. Lateral displacement and pile instability due to soil liquefaction using numerical model. Ain Shams Eng. J. 2014, 5, 1019–1032. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, L.; Ling, X.; Chan, A. Critical buckling load of pile in liquefied soil. Soil Dyn. Earthq. Eng. 2020, 135, 106197. [Google Scholar] [CrossRef]
- Bhattacharya, S. Safety Assessment of piled Buildings in Liquefiable Soils: Mathematical Tools. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Au, I.S.-K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–16. [Google Scholar]
- Basavana Gowda, G.M.; Dinesh, S.V.; Govindaraju, L.; Babu, R.R. Effect of Liquefaction Induced Lateral Spreading on Seismic Performance of Pile Foundations. Civ. Eng. J. 2021, 7, 58–70. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Adhikari, S.; Alexander, N.A. A simplified method for unified buckling and free vibration analysis of pile-supported structures in seismically liquefiable soils. Soil Dyn. Earthq. Eng. 2009, 29, 1220–1235. [Google Scholar] [CrossRef]
- Fernández-Escobar, C.J.; Vega-Posada, C.A.; Garcia-Aristizábal, E.F. Lateral deformation and buckling analysis of piles including shear effects: Numerical analysis. Eng. Struct. 2023, 277, 115416. [Google Scholar] [CrossRef]
- Han, J.; Frost, J.D. Load-Deflection response of transversely isotropic piles under lateral loads. Int. J. Numer. Anal. Methods Geomech. 2000, 24, 509–529. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Applicability of Timoshenko, Euler–Bernoulli and rigid beam theories in analysis of laterally loaded monopiles and piles. Géotechnique 2018, 68, 772–785. [Google Scholar] [CrossRef]
- Bechtel, A.J.; Krstic, V.; Hyde, A.; LaRegina, A. Importance of modelling shear effects for flexure of laterally loaded polymer piles. Int. J. Geotech. Eng. 2022, 16, 606–615. [Google Scholar] [CrossRef]
- Melchers, R.; Andre, T. Structural Reliability Assessment. In Structural Reliability Analysis and Prediction, 3rd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2017; pp. 31–61. [Google Scholar]
- Verma, A.K.; Srividya, A.; Karanki, D.R. (Eds.) Structural Reliability; Springer: London, UK, 2010; pp. 267–303. [Google Scholar]
- Guan, X.; He, J. Probabilistic Models for Reliability Analysis Using Safe-Life and Damage Tolerance Methods; Pham, H., Ed.; Springer: London, UK, 2023; pp. 965–979. [Google Scholar]
- Djami, A.B.N.; Samon, J.B.; Ousman, B.; Nguelcheu, U.N.; Nzié, W.; Ntamack, G.E.; Kenmeugne, B. Evaluation of the Reliability of a System: Approach by Monte Carlo Simulation and Application. Open J. Appl. Sci. 2024, 14, 721–739. [Google Scholar] [CrossRef]
- Ou, Y.; Wu, Y.; Cheng, J.; Chen, Y.; Zhao, W. Response Surface Method for Reliability Analysis Based on Iteratively-Reweighted-Least-Square Extreme Learning Machines. Electronics 2023, 12, 1741. [Google Scholar] [CrossRef]
- Thai, H.-T.; Thai, S.; Ngo, T.; Uy, B.; Kang, W.-H.; Hicks, S.J. Reliability considerations of modern design codes for CFST columns. J. Constr. Steel Res. 2021, 177, 106482. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and Invariant Second-Moment Code Format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Huang, J.; Griffiths, D.V. Observations on FORM in a simple geomechanics example. Struct. Saf. 2011, 33, 115–119. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Tokimatsu, K. Essential Criteria for design of piled foundations in seismically liquefiable areas. In Proceedings National Geotechnical Conference of Japan; Japanese Geotechnical Society: Niigata, Japan, 2004; pp. 1–2. [Google Scholar]
- Euler, L. A Method of Finding Curved Lines Enjoying the Maximum-Minimum Property, or the Solution of the Isoperimetric Problem in the Broadest Sense. Geneva, Switzerland. 1744, pp. 267–268. Available online: https://archive.org/details/methodusinvenie00eule/page/266/mode/2up (accessed on 27 August 2023).
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; McGraw-Hill Book Company, Inc.: New York City, NY, USA, 1963. [Google Scholar]
- Dong, Y.; Feng, Z.; He, J.; Chen, H.; Jiang, G.; Yin, H. Seismic Response of a Bridge Pile Foundation during a Shaking Table Test. Shock Vib. 2019, 2019, 9726013. [Google Scholar] [CrossRef]
- Fletcher, G.F.A. Standard Penetration Test: Its Uses and Abuses. J. Soil Mech. Found. Div. 1965, 91, 67–75. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified Procedure for Evaluating Soil Liquefaction Potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Iwasaki, T.; Arakawa, T.; Tokida, K.-I. Simplified procedures for assessing soil liquefaction during earthquakes. Int. J. Soil Dyn. Earthq. Eng. 1984, 3, 49–58. [Google Scholar] [CrossRef]
- Galupino, J.; Dungca, J. Estimating Liquefaction Susceptibility Using Machine Learning Algorithms with a Case of Metro Manila, Philippines. Appl. Sci. 2023, 13, 6549. [Google Scholar] [CrossRef]
- Sonmez, H. Modification of the liquefaction potential index and liquefaction susceptibility mapping for a liquefaction-prone area (Inegol, Turkey). Environ. Geol. 2003, 44, 862–871. [Google Scholar] [CrossRef]
- Subedi, M.; Acharya, I.P. Liquefaction hazard assessment and ground failure probability analysis in the Kathmandu Valley of Nepal. Geoenviron. Disasters 2022, 9, 1. [Google Scholar] [CrossRef]
- Li, D.; Juang, C.H.; Andrus, R. Liquefaction potential index: A critical assessment using probability concept. J. Geoengin. 2006, 1, 11–24. [Google Scholar] [CrossRef]
- Chen, L.-K.; Jiang, L.-Z.; Guo, W.; Liu, W.-S.; Zeng, Z.-P.; Chen, G.-W. The seismic response of high-speed railway bridges subjected to near-fault forward directivity ground motions using a vehicle-track-bridge element. Shock Vib. 2014, 2014, 985602. [Google Scholar] [CrossRef]
- Moayedi, H.; Kalantar, B.; Abdullahi, M.M.; Rashid, A.S.A.; Nazir, R.; Nguyen, H. Determination of Young Elasticity Modulus in Bored Piles Through the Global Strain Extensometer Sensors and Real-Time Monitoring Data. Appl. Sci. 2019, 9, 3060. [Google Scholar] [CrossRef]
- Pal, P. Dynamic Poisson’s Ratio and Modulus of Elasticity of Pozzolana Portland Cement Concrete. Int. J. Eng. Technol. Innov. 2019, 9, 131–144. Available online: https://ojs.imeti.org/index.php/IJETI/article/view/3132 (accessed on 10 September 2023).
- Aziz, H.Y.; Ma, J. Design and analysis of bridge foundation with different codes. J. Civ. Eng. Constr. Technol. 2011, 2, 101–118. Available online: https://api.semanticscholar.org/CorpusID:55998119 (accessed on 10 September 2023).
- Rouholamin, M.; Lombardi, D.; Bhattacharya, S. Experimental investigation of transient bending moment of piles during seismic liquefaction. Soil Dyn. Earthq. Eng. 2022, 157, 107251. [Google Scholar] [CrossRef]





| Date | Location | Magnitude | Comments |
|---|---|---|---|
| 1925 | California | 6.3 | The liquefaction during the Santa Barbara earthquake caused damage to the Sheffield Dam. |
| 1964 | Alaska | 9.2 | The effect of liquefaction during the Good Friday earthquake resulted in landslides and severe damage. |
| 1964 | Japan | 7.5 | Due to liquefaction, extensive damage to bridges, buildings, and port facilities in Niigata occurred. |
| 1971 | California | 6.6 | During the San Fernando earthquake, tremendous damage to the highway and buildings occurred. |
| 1989 | California | 7.1 | In San Francisco Bay, the Loma Prieta earthquake generated substantial ground amplification and damages due to liquefaction. |
| 1994 | California | 6.8 | The Northridge earthquake produced extreme shaking at various sites. |
| 1995 | Japan | 6.9 | The Hyogo-Ken Nanbu earthquake produced massive damage to Kobe. |
| 1999 | Turkey | 7.4 | The Kocaeli earthquake resulted in thousands of fatalities. |
| 2008 | China | 7.9 | A liquefaction event occurred in a densely populated area during the Wenchuan earthquake. |
| 2010 | New Zealand | 7.1 | Liquefaction happened during the Darfield earthquake, causing damage to a city. |
| 2011 | New Zealand | 6.2 | The Christchurch earthquake also caused damage to cities due to liquefaction. |
| 2023 | Turkey and Syria | 7.7 | On 6 February 2023, a strong earthquake doublet of Mw 7.7 and Mw 7.6 occurred in Turkey and Syria, respectively. The earthquake caused liquefaction and lateral spreading, resulting in a death toll of over 52,000 and making it the fifth-deadliest earthquake of the 21st century. |
| Parameters | Value |
|---|---|
| Length of girder | 32 m |
| Width of girder | 12 m |
| Height of girder | 3.05 m |
| Area of girder | 8.6597 m2 |
| Linear mass of girder | 2.19 × 104 kg/m |
| Length of pier column in cross-section | 6.20 m |
| Width of pier column in cross-section | 2.20 m |
| Height of pier column nos. 1–6 | 10 m, 12 m, 14 m, 16 m, 18 m, and 20 m |
| Area of solid pier (round-shaped) | 11.141 m2 |
| Unit weight of concrete | 24 kN/m3 |
| Superimposed dead load | 184 kN/m |
| Parameters | Value | From the Study by |
|---|---|---|
| E | 25,000,000 KPa | Moayedi et al. [52] |
| 0.35 | Bhattacharya [25] | |
| n | 1.11 | Timoshenko and Gere [42] |
| α | 1.32 | Dong et al. [43] |
| ν | 0.2 | Pal [53] |
| K | 1.00 | Madabhushi et al. [12] |
| Train load | 83.60 kN/m | Aziz and Ma [54] |
| Parameters | Value |
|---|---|
| μLcrit | Based on the calculated Lcrit, which depends on various pile diameters, and Pdyn generated from Table 2. |
| μLuns | 10.00 m |
| σLcrit | Based on the calculated Lcrit, which depends on various pile diameters, and Pdyn generated from Table 2. |
| σLuns | 7.74798 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachinilla, B.; Siddhpura, M.; Evangelista, A.; Hammad, A.W.; Haddad, A.N. Buckling Instability of Monopiles in Liquefied Soil via Structural Reliability Assessment Framework. Infrastructures 2024, 9, 123. https://doi.org/10.3390/infrastructures9080123
Bachinilla B, Siddhpura M, Evangelista A, Hammad AW, Haddad AN. Buckling Instability of Monopiles in Liquefied Soil via Structural Reliability Assessment Framework. Infrastructures. 2024; 9(8):123. https://doi.org/10.3390/infrastructures9080123
Chicago/Turabian StyleBachinilla, Brian, Milind Siddhpura, Ana Evangelista, Ahmed WA Hammad, and Assed N. Haddad. 2024. "Buckling Instability of Monopiles in Liquefied Soil via Structural Reliability Assessment Framework" Infrastructures 9, no. 8: 123. https://doi.org/10.3390/infrastructures9080123








