Novel Single-Shot Diagnostics for Electrons from Laser-Plasma Interaction at SPARC_LAB
Abstract
:1. Introduction
2. EOS Diagnostics for fs Resolution Probing High Intensity Laser–Solid Target Interaction
2.1. Experimental Setup
2.2. Experimental Results
3. Correlation Term Reconstruction for Single-Shot Emittance Measurements through Incoherent OTR
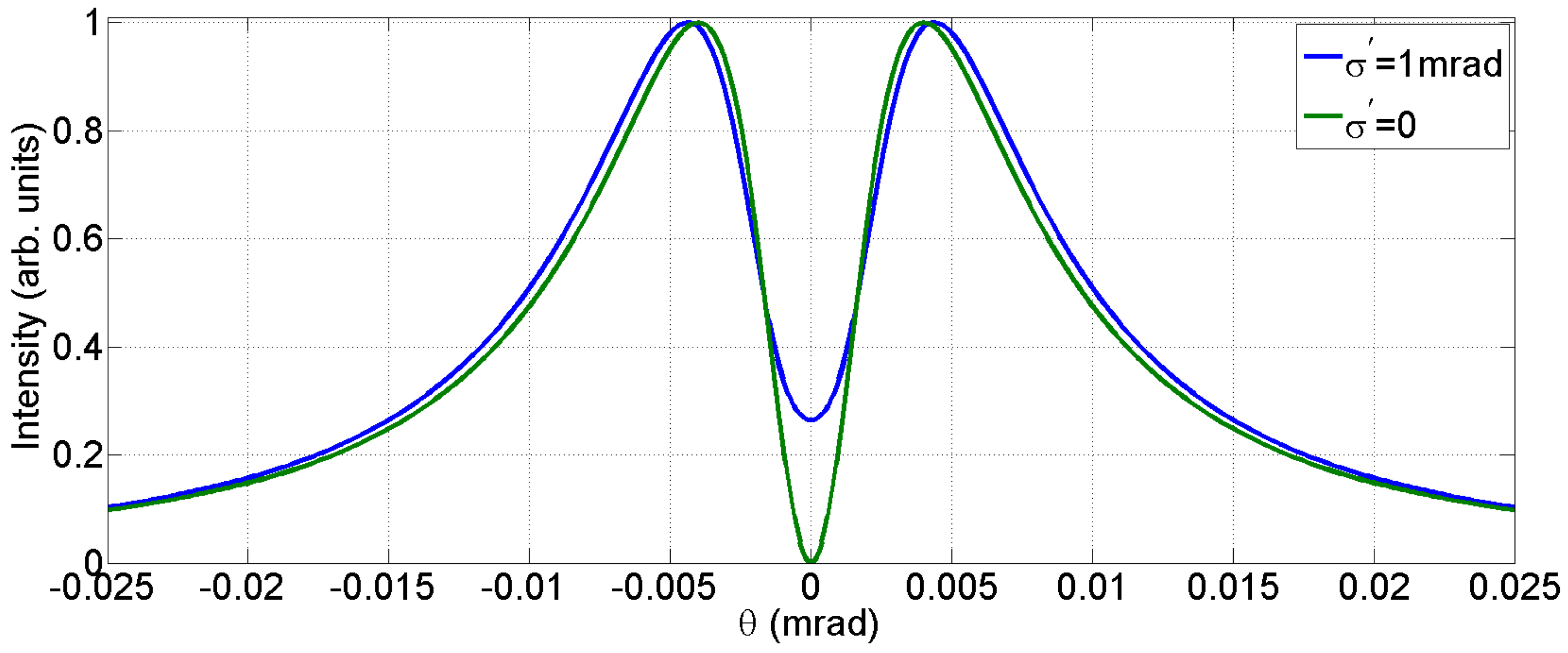
Experimental Setup
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Remington, B.A.; Arnett, D.; Paul, R.; Takabe, H. Modeling astrophysical phenomena in the laboratory with intense lasers. Science 1999, 284, 1488–1493. [Google Scholar] [CrossRef]
- Roth, M.; Cowan, T.; Key, M.; Hatchett, S.; Brown, C.; Fountain, W.; Johnson, J.; Pennington, D.; Snavely, R.; Wilks, S.; et al. Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 2001, 86, 436. [Google Scholar] [CrossRef] [PubMed]
- Rousse, A.; Phuoc, K.T.; Shah, R.; Pukhov, A.; Lefebvre, E.; Malka, V.; Kiselev, S.; Burgy, F.; Rousseau, J.P.; Umstadter, D.; et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys. Rev. Lett. 2004, 93, 135005. [Google Scholar] [CrossRef] [PubMed]
- Curcio, A.; Anania, M.; Bisesto, F.; Chiadroni, E.; Cianchi, A.; Ferrario, M.; Filippi, F.; Giulietti, D.; Marocchino, A.; Petrarca, M.; et al. Trace-space reconstruction of low-emittance electron beams through betatron radiation in laser-plasma accelerators. Phys. Rev. Accel. Beams 2017, 20, 012801. [Google Scholar] [CrossRef]
- Curcio, A.; Anania, M.; Bisesto, F.; Faenov, A.; Ferrario, M.; Galletti, M.; Giulietti, D.; Kodama, R.; Petrarca, M.; Pikuz, T.; et al. Characterization of X-ray radiation from solid Sn target irradiated by femtosecond laser pulses in the presence of air plasma sparks. Laser Part. Beams 2016, 34, 533–538. [Google Scholar] [CrossRef]
- Tajima, T.; Dawson, J. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Geddes, C.; Toth, C.; Van Tilborg, J.; Esarey, E.; Schroeder, C.; Bruhwiler, D.; Nieter, C.; Cary, J.; Leemans, W. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 2004, 431, 538–541. [Google Scholar] [CrossRef] [PubMed]
- Leemans, W.; Nagler, B.; Gonsalves, A.; Tóth, C.; Nakamura, K.; Geddes, C.; Esarey, E.; Schroeder, C.; Hooker, S. GeV electron beams from a centimetre-scale accelerator. Nat. Phys. 2006, 2, 696–699. [Google Scholar] [CrossRef]
- Maksimchuk, A.; Gu, S.; Flippo, K.; Umstadter, D.; Bychenkov, V.Y. Forward ion acceleration in thin films driven by a high-intensity laser. Phys. Rev. Lett. 2000, 84, 4108. [Google Scholar] [CrossRef] [PubMed]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751. [Google Scholar]
- Ferrario, M.; Alesini, D.; Anania, M.; Bacci, A.; Bellaveglia, M.; Bogdanov, O.; Boni, R.; Castellano, M.; Chiadroni, E.; Cianchi, A.; et al. SPARC_LAB present and future. Nucl. Instrum. Methods Phys. Res. Sec. B Beam Interact. Mater. At. 2013, 309, 183–188. [Google Scholar] [CrossRef] [Green Version]
- Jamison, S.P.; Shen, J.; MacLeod, A.M.; Gillespie, W.; Jaroszynski, D.A. High-temporal-resolution, single-shot characterization of terahertz pulses. Opt. Lett. 2003, 28, 1710–1712. [Google Scholar] [CrossRef] [PubMed]
- Helle, M.; Gordon, D.; Kaganovich, D.; Ting, A. Extending electro-optic detection to ultrashort electron beams. Phys. Rev. Spec. Top.-Accel. Beams 2012, 15, 052801. [Google Scholar] [CrossRef]
- Popescu, H.; Baton, S.; Amiranoff, F.; Rousseaux, C.; Le Gloahec, M.R.; Santos, J.; Gremillet, L.; Koenig, M.; Martinolli, E.; Hall, T.; et al. Subfemtosecond, coherent, relativistic, and ballistic electron bunches generated at ω 0 and 2 ω 0 in high intensity laser-matter interaction. Phys. Plasmas 2005, 12, 063106. [Google Scholar] [CrossRef]
- Jung, R.; Osterholz, J.; Löwenbrück, K.; Kiselev, S.; Pretzler, G.; Pukhov, A.; Willi, O.; Kar, S.; Borghesi, M.; Nazarov, W.; et al. Study of electron-beam propagation through preionized dense foam plasmas. Phys. Rev. Lett. 2005, 94, 195001. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.; Amiranoff, F.; Baton, S.; Gremillet, L.; Koenig, M.; Martinolli, E.; Le Gloahec, M.R.; Rousseaux, C.; Batani, D.; Bernardinello, A.; et al. Fast electron transport in ultraintense laser pulse interaction with solid targets by rear-side self-radiation diagnostics. Phys. Rev. Lett. 2002, 89, 025001. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.; Debayle, A.; Nicolaï, P.; Tikhonchuk, V.; Manclossi, M.; Batani, D.; Guemnie-Tafo, A.; Faure, J.; Malka, V.; Honrubia, J. Fast-electron transport and induced heating in aluminum foils. Phys. Plasmas 2007, 14, 103107. [Google Scholar] [CrossRef]
- Storm, M.; Solodov, A.; Myatt, J.; Meyerhofer, D.; Stoeckl, C.; Mileham, C.; Betti, R.; Nilson, P.; Sangster, T.; Theobald, W.; et al. High-current, relativistic electron-beam transport in metals and the role of magnetic collimation. Phys. Rev. Lett. 2009, 102, 235004. [Google Scholar] [CrossRef] [PubMed]
- Bellei, C.; Nagel, S.; Kar, S.; Henig, A.; Kneip, S.; Palmer, C.; Sävert, A.; Willingale, L.; Carroll, D.; Dromey, B.; et al. Micron-scale fast electron filaments and recirculation determined from rear-side optical emission in high-intensity laser–solid interactions. New J. Phys. 2010, 12, 073016. [Google Scholar] [CrossRef]
- Pompili, R.; Anania, M.; Bisesto, F.; Botton, M.; Castellano, M.; Chiadroni, E.; Cianchi, A.; Curcio, A.; Ferrario, M.; Galletti, M.; et al. Sub-picosecond snapshots of fast electrons from high intensity laser-matter interactions. Opt. Express 2016, 24, 29512–29520. [Google Scholar] [CrossRef] [PubMed]
- Bisesto, F.; Anania, M.; Chiadroni, E.; Cianchi, A.; Costa, G.; Curcio, A.; Ferrario, M.; Galletti, M.; Pompili, R.; Schleifer, E.; et al. Innovative single-shot diagnostics for electrons accelerated through laser-plasma interaction at FLAME. In Proceedings of the 2017 SPIE Optics + Optoelectronics, Prague, Czech Republic, 24–27 April 2017; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; p. 102400. [Google Scholar]
- Pompili, R.; Anania, M.; Bisesto, F.; Botton, M.; Castellano, M.; Chiadroni, E.; Cianchi, A.; Curcio, A.; Ferrario, M.; Galletti, M.; et al. Femtosecond dynamics of energetic electrons in high intensity laser-matter interactions. Sci. Rep. 2016, 6, 35000. [Google Scholar] [CrossRef] [PubMed]
- Bisesto, F.; Anania, M.P.; Chiadroni, E.; Cianchi, A.; Curcio, A.; Ferrario, M.; Pompili, R.; Zigler, A. Innovative single-shot diagnostics for electrons from laser wakefield acceleration at FLAME. In Proceedings of the 8th International Particle Accelerator Conference (IPAC’17), Copenhagen, Denmark, 14–19 May 2017; JACoW: Geneva, Switzerland, 2017; pp. 1727–1730. [Google Scholar]
- Cianchi, A.; Anania, M.; Bellaveglia, M.; Bisesto, F.; Castellano, M.; Chiadroni, E.; Di Giovenale, D.; Di Pirro, G.; Ferrario, M.; Gatti, G.; et al. Transverse emittance diagnostics for high brightness electron beams. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 2017, 865, 63–66. [Google Scholar] [CrossRef]
- Clark, E.; Krushelnick, K.; Zepf, M.; Beg, F.; Tatarakis, M.; Machacek, A.; Santala, M.; Watts, I.; Norreys, P.; Dangor, A. Energetic heavy-ion and proton generation from ultraintense laser-plasma interactions with solids. Phys. Rev. Lett. 2000, 85, 1654. [Google Scholar] [CrossRef] [PubMed]
- Snavely, R.; Key, M.; Hatchett, S.; Cowan, T.; Roth, M.; Phillips, T.; Stoyer, M.; Henry, E.; Sangster, T.; Singh, M. Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys. Rev. Lett. 2000, 85, 2945. [Google Scholar] [CrossRef] [PubMed]
- Mackinnon, A.; Sentoku, Y.; Patel, P.; Price, D.; Hatchett, S.; Key, M.; Andersen, C.; Snavely, R.; Freeman, R. Enhancement of proton acceleration by hot-electron recirculation in thin foils irradiated by ultraintense laser pulses. Phys. Rev. Lett. 2002, 88, 215006. [Google Scholar] [CrossRef] [PubMed]
- Dubois, J.L.; Lubrano-Lavaderci, F.; Raffestin, D.; Ribolzi, J.; Gazave, J.; La Fontaine, A.C.; d’Humières, E.; Hulin, S.; Nicolaï, P.; Poyé, A. Target charging in short-pulse-laser-plasma experiments. Phys. Rev. E 2014, 89, 013102. [Google Scholar] [CrossRef] [PubMed]
- Wilks, S.; Langdon, A.; Cowan, T.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.; Pennington, D.; MacKinnon, A.; Snavely, R. Energetic proton generation in ultra-intense laser-solid interactions. Phys. Plasmas 2001, 8, 542–549. [Google Scholar] [CrossRef]
- Mora, P. Plasma expansion into a vacuum. Phys. Rev. Lett. 2003, 90, 185002. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.K.; Cui, Y.; Chatterjee, G.; Adak, A.; Wang, W.; Ahmed, S.; Lad, A.D.; Sheng, Z.; Kumar, G.R. Direct observation of ultrafast surface transport of laser-driven fast electrons in a solid target. Phys. Plasmas 2013, 20, 110701. [Google Scholar] [CrossRef]
- Poyé, A.; Hulin, S.; Bailly-Grandvaux, M.; Dubois, J.L.; Ribolzi, J.; Raffestin, D.; Bardon, M.; Lubrano-Lavaderci, F.; D’Humières, E.; Santos, J.J. Physics of giant electromagnetic pulse generation in short-pulse laser experiments. Phys. Rev. E 2015, 91, 043106. [Google Scholar] [CrossRef] [PubMed]
- Jäckel, O.; Polz, J.; Pfotenhauer, S.; Schlenvoigt, H.; Schwoerer, H.; Kaluza, M. All-optical measurement of the hot electron sheath driving laser ion acceleration from thin foils. New J. Phys. 2010, 12, 103027. [Google Scholar] [CrossRef]
- Nilson, P.; Davies, J.; Theobald, W.; Jaanimagi, P.; Mileham, C.; Jungquist, R.; Stoeckl, C.; Begishev, I.; Solodov, A.; Myatt, J. Time-resolved measurements of hot-electron equilibration dynamics in high-intensity laser interactions with thin-foil solid targets. Phys. Rev. Lett. 2012, 108, 085002. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, A.; Dharmadhikari, A.; Rajeev, P.; Kumar, G.R.; Sengupta, S.; Das, A.; Kaw, P. Laser-generated ultrashort multimegagauss magnetic pulses in plasmas. Phys. Rev. Lett. 2002, 89, 225002. [Google Scholar] [CrossRef] [PubMed]
- Key, M.; Cable, M.; Cowan, T.; Estabrook, K.; Hammel, B.; Hatchett, S.; Henry, E.; Hinkel, D.; Kilkenny, J.; Koch, J.; et al. Hot electron production and heating by hot electrons in fast ignitor research. Phys. Plasmas 1998, 5, 1966–1972. [Google Scholar] [CrossRef]
- Ping, Y.; Shepherd, R.; Lasinski, B.; Tabak, M.; Chen, H.; Chung, H.; Fournier, K.; Hansen, S.; Kemp, A.; Liedahl, D.; et al. Absorption of short laser pulses on solid targets in the ultrarelativistic regime. Phys. Rev. Lett. 2008, 100, 085004. [Google Scholar] [PubMed]
- Santala, M.; Zepf, M.; Watts, I.; Beg, F.; Clark, E.; Tatarakis, M.; Krushelnick, K.; Dangor, A.; McCanny, T.; Spencer, I.; et al. Effect of the plasma density scale length on the direction of fast electrons in relativistic laser-solid interactions. Phys. Rev. Lett. 2000, 84, 1459. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Shepherd, R.; Chung, H.; Kemp, A.; Hansen, S.; Wilks, S.; Ping, Y.; Widmann, K.; Fournier, K.; Dyer, G.; et al. Fast-electron-relaxation measurement for laser-solid interaction at relativistic laser intensities. Phys. Rev. E 2007, 76, 056402. [Google Scholar] [CrossRef] [PubMed]
- Wilke, I.; MacLeod, A.M.; Gillespie, W.; Berden, G.; Knippels, G.; Van Der Meer, A. Single-shot electron-beam bunch length measurements. Phys. Rev. Lett. 2002, 88, 124801. [Google Scholar] [CrossRef] [PubMed]
- Steffen, B.; Arsov, V.; Berden, G.; Gillespie, W.; Jamison, S.; MacLeod, A.M.; Van Der Meer, A.; Phillips, P.; Schlarb, H.; Schmidt, B. Electro-optic time profile monitors for femtosecond electron bunches at the soft X-ray free-electron laser FLASH. Phys. Rev. Spec. Top.-Accel. Beams 2009, 12, 032802. [Google Scholar] [CrossRef]
- Pompili, R.; Anania, M.P.; Bellaveglia, M.; Biagioni, A.; Castorina, G.; Chiadroni, E.; Cianchi, A.; Croia, M.; Giovenale, D.D.; Ferrario, M.; et al. Femtosecond timing-jitter between photo-cathode laser and ultra-short electron bunches by means of hybrid compression. New J. Phys. 2016, 18, 083033. [Google Scholar] [CrossRef]
- Cavalieri, A.L.; Fritz, D.; Lee, S.; Bucksbaum, P.; Reis, D.; Rudati, J.; Mills, D.; Fuoss, P.; Stephenson, G.; Kao, C. Clocking femtosecond X-rays. Phys. Rev. Lett. 2005, 94, 114801. [Google Scholar] [CrossRef] [PubMed]
- Löhl, F.; Schreiber, S.; Castellano, M.; Di Pirro, G.; Catani, L.; Cianchi, A.; Honkavaara, K. Measurements of the transverse emittance at the FLASH injector at DESY. Phys. Rev. Spec. Top.-Accel. Beams 2006, 9, 092802. [Google Scholar] [CrossRef]
- Mostacci, A.; Bellaveglia, M.; Chiadroni, E.; Cianchi, A.; Ferrario, M.; Filippetto, D.; Gatti, G.; Ronsivalle, C. Chromatic effects in quadrupole scan emittance measurements. Phys. Rev. Spec. Top.-Accel. Beams 2012, 15, 082802. [Google Scholar] [CrossRef]
- Ter-Mikaelian, M.L. High Energy Electromagnetic Processes in Condensed Media; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Rule, D. Transition radiation diagnostics for intense charged particle beams. Nucl. Instrum. Methods Phys. Res. Sec. B Beam Interact. Mater. At. 1987, 24, 901–904. [Google Scholar] [CrossRef]
- Castellano, M.; Verzilov, V. Spatial resolution in optical transition radiation beam diagnostics. Phys. Rev. Spec. Top.-Accel. Beams 1998, 1, 062801. [Google Scholar] [CrossRef]
- Bosser, J.; Mann, J.; Ferioli, G.; Warts, L. Optical transition radiation proton beam profile monitor. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 1985, 238, 45–52. [Google Scholar] [CrossRef]
- Wartski, L.; Marcou, J.; Roland, S. Detection of optical transition radiation and its application to beam diagnostics. IEEE Trans. Nucl. Sci. 1973, 20, 544–548. [Google Scholar] [CrossRef]
- Chiadroni, E.; Castellano, M.; Cianchi, A.; Honkavaara, K.; Kube, G. Effects of transverse electron beam size on transition radiation angular distribution. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 2012, 673, 56–63. [Google Scholar] [CrossRef]
- Feldman, R.; Lumpkin, A.; Rule, D.; Fiorito, R. Developments in on-line, electron-beam emittance measurements using optical-transition radiation techniques. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 1990, 296, 193–198. [Google Scholar] [CrossRef]
- Zemax 13 Optical Design Program User’s Manual; Zemax LLC: Seattle, WA, USA, 2014.
- Castellano, M.; Cianchi, A.; Orlandi, G.; Verzilov, V. Effects of diffraction and target finite size on coherent transition radiation spectra in bunch length measurements. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 1999, 435, 297–307. [Google Scholar] [CrossRef]
- Bisesto, F.; Anania, M.; Bacci, A.; Bellaveglia, M.; Chiadroni, E.; Cianchi, A.; Curcio, A.; Di Giovenale, D.; Di Pirro, G.; Ferrario, M.; et al. Laser-capillary interaction for the EXIN project. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 2016, 829, 309–313. [Google Scholar] [CrossRef]
- Rossi, A.; Anania, M.; Bacci, A.; Belleveglia, M.; Bisesto, F.; Chiadroni, E.; Cianchi, A.; Curcio, A.; Gallo, A.; Di Giovenale, D.; et al. Stability study for matching in laser driven plasma acceleration. Nucl. Instrum. Methods Phys. Res. Sec. A Accel. Spectrom. Detect. Assoc. Equip. 2016, 829, 67–72. [Google Scholar] [CrossRef]










© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bisesto, F.; Anania, M.P.; Botton, M.; Chiadroni, E.; Cianchi, A.; Curcio, A.; Ferrario, M.; Galletti, M.; Pompili, R.; Schleifer, E.; et al. Novel Single-Shot Diagnostics for Electrons from Laser-Plasma Interaction at SPARC_LAB. Quantum Beam Sci. 2017, 1, 13. https://doi.org/10.3390/qubs1030013
Bisesto F, Anania MP, Botton M, Chiadroni E, Cianchi A, Curcio A, Ferrario M, Galletti M, Pompili R, Schleifer E, et al. Novel Single-Shot Diagnostics for Electrons from Laser-Plasma Interaction at SPARC_LAB. Quantum Beam Science. 2017; 1(3):13. https://doi.org/10.3390/qubs1030013
Chicago/Turabian StyleBisesto, Fabrizio, Maria Pia Anania, Mordechai Botton, Enrica Chiadroni, Alessandro Cianchi, Alessandro Curcio, Massimo Ferrario, Mario Galletti, Riccardo Pompili, Elad Schleifer, and et al. 2017. "Novel Single-Shot Diagnostics for Electrons from Laser-Plasma Interaction at SPARC_LAB" Quantum Beam Science 1, no. 3: 13. https://doi.org/10.3390/qubs1030013
APA StyleBisesto, F., Anania, M. P., Botton, M., Chiadroni, E., Cianchi, A., Curcio, A., Ferrario, M., Galletti, M., Pompili, R., Schleifer, E., & Zigler, A. (2017). Novel Single-Shot Diagnostics for Electrons from Laser-Plasma Interaction at SPARC_LAB. Quantum Beam Science, 1(3), 13. https://doi.org/10.3390/qubs1030013








