1. Spatial Energy Distribution Released by High Energy Particle in Organic Substances
Since the dawn of quantum mechanical aspects of atoms and molecules, interactions of ionizing radiations with condensed matters has been at the center of analytical techniques, in order to determine the electronic structures of them [
1,
2,
3,
4]. Particularly the Coulombic interactions between charged particles with a relatively high momentum and electrons confined in their orbitals have been discussed precisely in terms of the experimental energy loss of the incident charged particles, and/or cross section of ionization events induced in the target condensed matters [
5,
6]. For the quantitative experimental analysis of the loss/events in the system, X-rays/γ-rays and high energy electron beams have often been popular choices because of the homogeneity of the released energy from the ionizing radiation into the target matters, which helps statistical counting of the events/resulting products and intermediates by conventional analysis protocols such as spectroscopic/microscopic techniques [
7,
8]. In contrast to the classical ionizing radiation applied to reveal atomic/molecular structures, heavy charged particles also play a significant role to clarify the structures, as evident in the initial success of Rutherford scattering experiments via momentum transfer from an incident charged particle to the target atoms. Thus, the energy dissipation processes from the incident charged particles draw the attention of scientists working on condensed matter physics, nuclear physics, astrophysics, etc. For instance, the visualization of high energy charged particle tracks in organic/inorganic matters was successfully applied to assess the energy/momentum of the incident charged particles, giving clear evidence of nuclear reactions caused by the particles [
9]. By 20th century, the theoretical background used for interpreting these interactions has been well developed in correlation with experimental observation, leading to sophisticated formulations. The initial benchmark of the formulation was first established by Bethe [
10,
11], starting from a simple binary elastic collision model in terms of transferred energy (
) from one particle to the other. When we consider elastic collisions between an incident particle and an electron in the target atoms, its differential cross section (
) of the incident particle can be represented as,
where
and
are the atomic number and the velocity of the incident particle, while
and
are mass of electron and an elementary charge, respectively.
Now, the ionization events in the condensed phases as well as successive chemical reaction in the matter are considered as inelastic collision events for an incident particle [
12]. Ionization cross section in classical Thomson model could be delivered by Equation (1) based on the Rutherford scattering scheme [
2,
13]. However, more detailed discussions were initiated by Born with quantum mechanical views of target substances with a general wave function of their frontier orbital:
which can be derived by a general Schrödinger equation as,
and the solutions of Equation (2) are given with the use of Green’s function of
and an incident plane-wave function
as [
14],
Here we obtain,
under the following requirements for
and
of
and
Considering only the contribution of the outgoing wave function from
leading to
, the solution of the above Schrödinger equation is given by Lippmann-Schwinger equation as [
15],
Here, we presume
, the norm of displacement vector can be represented by,
then we obtain a simplified expression of form for Green’s function as,
By substituting this into Equation (7), the resulting wave function of the target is represented as,
To lead an explicit analytical solution for
of electrons responsible to the first ionization energy of the target materials, we use the Born approximation to Equation (7), expanded with Born series [
16], and take the first order expansion as an approximate as follows,
By comparing Equation (11) to (10), provisionally, the solution has been obtained as,
Here,
is a unit vector. The wave vectors in the integrant can be substituted by,
and the simplified wave function is given by,
The second term in Equation (14) is responsible for the inelastic energy loss of an incident particle which can be transferred to the target. If we discuss the term separatory as a function of
, Equation (14) can be rewritten as,
and
respectively. Now the differential inelastic cross section of
can be formulated clearly as,
where
is the differential solid angle. With the measure of momentum of the incident particle prior after the collision events as
and
, respectively, Equation (17) can be derived as,
where
is the Coulombic potential between the particles as represented simply by,
Then, the integration over
r can be written by,
Thus, Equation (18) transforms into follows with an atomic matrix element called as the Fano factor:
[
17,
18].
and
where
u is the eigenfunction of electron orbital in the target. Considering the energy and momentum consevation law, we obtain a relationship between
and
given as,
Therefore Equation (21) is eqivalent to:
The given kinetic energy transferred to an electron as
into Equation (24),
can be finally appeared as,
Now, we have obtained the theoretical differential cross section of the incident particle in an inelastic collision event [
18].
The statistical treatment of the collision events within the matter will lead to an overall energy loss of an incident particle along the particle trajectory. Now, the averaged energy loss (
) of the particle per unit length of the trajectory is defined by:
where
is the number density of atoms in the target. In this study, the energy delivered by the incident particle to the molecular materials is predominantly consumed as ionization events, where the velocity of an incident particle is relatively larger than the angular momentum of electrons bound to the molecules. Here, we only treat the case of the larger velocity than the Massey’s criterion [
19],
is given from Equation (1) by,
where
equals to
, and
depends on the ionization potentials of chemical substances in the target. If the discrete energy levels of electrons bound in the target molecule are given by
, an accurate expression of the integration in the above equation should be,
Now, the density of states for electrons in the target matter are high enough to average by numerical integration over the range of
, and the summation can be parameterized by an averaged ionization potential of
as [
20],
Then,
can be expressed with
as,
The direct energy transfer from the incident particle to the target matter below its ionization potentials can be calculated based on the total transition dipoles of the target molecular substances. The generalized oscillator strength (
) corresponding to a discrete energy level with a quantum number of
can be represented by
as,
Here, the oscillator strength is defined as a function of transferred energy to the molecular substances (
). Thus, the total energy loss by this scheme can be calculated by,
For
, it’s summing up should be equal to the total number of electrons in the target, i.e., Fermi’s golden rule. This can be simply represented by,
and again the oscillator strength is correlated directly to
as,
Substituting Equation (34) into Equation (31), we obtain,
This shows a striking contrast to Equation (30), showing an equal contribution of energy transfer above and below
, the averaged ionization potential. Finally, the overall value of
can be,
Based on this equation, the spatial distribution of released energy by an incident particle is discussed in an isolated particle track.
Since the quantum mechanical description of electronic stopping was proposed for the first time by Bethe [
10,
11] in 1930′s, a number of further theoretical approaches have been continuously discussed, aiming for a more precise estimation of stopping power within variable energy regimes of the incident charged particles. Particularly in the high-velocity regime (above 1 MeV/u), the relativistic effects were taken into accounts by Bloch [
21], the shell correction and the density effect correction by Fano [
22], and the effective charge correction by Bohr and Northcliff [
23,
24], respectively. In the low-velocity regime (significantly below 1 MeV/u), nuclear stopping becomes predominant resulting in developments of the non-perturbative stopping models based on the electron exchange within the collision events by Firsov [
25], the Thomas-Fermi model by Lindhard and Scharff [
26], and the electron gas model by Fermi and Teller [
27]. At the later stage of the collision cascades, a high energy charged particle penetrates the target with slowing down to as represented by
in Equation (27). Here, the electronic stopping can no longer be derived from a series of separable binary collisions because of the complicated energy exchange between the particle and the target electrons, which is often referred to as “electron–phonon coupling”. Several theories have therefore been proposed, embedding new electronic and nuclear stopping mechanisms: two-temperature models [
28], the Coulomb explosion model [
29], and thermal spike model [
30].
Overcoming these complexities due to variable velocity-dependent electronic stopping processes, quantum-mechanical descriptions by the use of first-principle calculations have attracted attention since the 1980s [
31,
32,
33,
34]. These approaches have striking advantages in terms of the non-empirical calculation of electronic stopping over a wide range of particle velocities, including the stopping power maximum. The rapid development of computational capabilities, such as peta-scale or exa-scale supercomputers, have also realized the direct simulation of the electron dynamics of the system incorporating the quantum-mechanical effects, which now allows us to estimate precisely the mean energy transfer within many-body and complicated molecules with time-dependent density functional theory (TDDFT) simulations. The protocols to assess the energy transfer are based on a simple scheme to predict the distinct initial and final states of the systems with Kohn–Sham orbitals as:
and the dynamic potential of
has been simulated in every step with short enough time intervals. In the most recent cases, the steps were divided into 2 at, revealing gradual changes of the energy state of each target molecule [
35]. In this regard, further detailed models were developed rapidly in sequence, taking self-consistent, non-perturbative, and time-lapse treatment of electron dynamics into account for metals [
36,
37,
38], semiconductors [
39,
40], and biomolecules [
41,
42].
The origin of the organic molecules on Earth, eventually “D’où venons-nous?”, has been a long-lasting unsolved fundamental question and remains worth discussing to date. Since a model reported for the origin of biomolecular homochirality involving extraterrestrial source of circularly polarized light by Rubinstein et al. [
43], the polarized UV light has been regarded as the likeliest and most powerful energy source to initiate an imbalance in the enantiomers of organic molecules both in space and on Earth. The scenario has been widely supported and developed by numerous experimental evidences [
44,
45]. In reality, enantiomeric excesses were actually induced in solid-state leucine samples by circularly polarized synchrotron radiation, simulating astronomical sources such as neutron stars/magnetic white dwarfs [
46].
One of the other plausible scenarios is related to radiation-induced reactions in the context of X-, and γ-rays, high energy electrons/protons in solar radiations, and heavy charged particles from our galaxy: a full stream of ionizing radiations. Various organic molecules have been found in space. Even complex organic molecules were detected from the dusts blasted out from comets. It has been considered that small molecules such as H
2O, CO, and NH
3 frozen at the surface of interstellar dusts cause chemical reactions by cosmic radiation to generate organic molecules. A simulating experiment revealed that amino acids were generated by irradiating these small molecules with ultraviolet radiations at 12 K [
47].
The other important and attractive topic yet unsolved is the origin of homochirality in the earth—why natural amino acids are the L-form while D-forms are enriched for sugars [
48]. Since the enrichment of one isomer was found not only in the earth, but also in some meteorites [
49], the cosmic scenario has been supported by many works, and may give a convincing answer to the origin of homochirality. In light of the higher angular momentum of non-spherical multi-atomic particles than that of ultra-violet light or spin-polarized electrons, the particle induced intra-track chemical reactions will be a powerful candidate to lead an excess of one enantiomer, approaching the start of life.
2. Single Particle Nanofabrication Technique (SPNT) as a Versatile Tool for Nanofabrication
Ionizing radiations including high energy charged particles are ubiquitous in our daily life, particularly the later present in solar radiations. Quantitative analysis of the energy deposition by the ionizing radiations is crucial for sustainability of lives and materials, however the dosimetry of cosmic rays with a variety of particles and a broad energy spectrum have been challenging to date. Ionizing radiation met polymeric materials in the beginning of 20th century [
50,
51] as a powerful tool of functionalization by chemical reactions induced via reactive intermediates such as ions, ion radicals, and neutral radials. The reactive intermediates, distributed homogeneously in the bulk polymeric materials, promote crosslinking, main chain scission, and subsequent graft polymerization reactions, which often dramatically improve the physical and mechanical properties of the polymeric materials [
52]. Focusing on the functionalization of tons of polymeric materials, the primary choices of the ionizing radiations to lead the intermediates have been γ-rays and/or high energy electrons because of their high permeability into the materials with the lower
, securing the homogeneity of spatial distribution of the intermediates [
53]. In contrast, a high energy heavy charged particle with higher orders of
has attracted much attention because of the intensive spatial distribution of the released energy, and hence the intermediates, leading to a unique chemical reaction which has never been realized in the context of bulk thermal/mechanical/photo-induced chemical reactions [
54].
The severe damage to organic substances induced by the particle have been of particular interest to visualize the particle track in the materials for a long time as noted, and area of the latent tracks in the materials can be facilely etched, modified, and re-filled by the chemical protocols after irradiation [
55]. The resulting nano/micro holes and beers provide unique nanospaces with an extremely high aspect ratio, and are developed as platforms for a variety of functional materials [
56].
In view of the dosimetry of cosmic rays of high energy charged particles, several calculation codes such as CREME96 have been developed based on the numerical modelling of events caused by ionizing radiations to predict cosmic ray effects onto materials and devices in the last decade [
57]. The rapid development of such calculation codes allows us to evaluate separately and precisely the effects of a variety of charged particles with a broad energy spectrum. An experimental approach to micro-dosimetry for a charged particle has been also investigated vigorously as seen in the “ion track membrane” works, where each latent track of a charged particle in a polymeric film could be etched chemically and visualized microscopically [
58]. Numerous information concerning an incident charged particles such as momentum, charged state, and kinetic energy could be delivered by the size and direction of the visualized “nano holes”.
Generally, the kinetic energy loss of the particle is negligible in a target of μm-thick organic polymer film for the heavy charged particle with tens MeV kinetic energy, preserving the linearity and uniformity of a latent track and the resulting “etched nanoholes”. The engineering of the sizes and shapes of the “nano holes” has also been widely studied and developed by the subsequent chemical etching protocols to the latent track formation. The linearity of a “nano hole” reflects precisely the momentum of an incident particles, thus the network structure of the “nano hole” aggregates with controlled orientation can be applicable to form 3D holographic structures [
59]. A simple approach to utilize “nano holes” is the formation of polymeric nano-porous membranes with selective ion transport and tuned permeability to the solutions. In the nano-porous membrane systems, the ion selectivity is engaged in interplay with the solvent permeability, and it is indispensable to tune the size and uniformity of the nano-pore precisely to overcome the above interplay and realize the sharp selectivity with high enough permeability [
60]. The “nano holes” given by the high energy charged particles have been regarded as ideal platforms to solve the above issues in nano-porous membranes, of which application to those for fuel cells has been launched recently [
61].
Functionalization of the “nano holes” has been of interest since the first discovery of particle tracks. The “nano holes” formed by the track etching could be worked as nano channels responding to external stimuli such as an electric field and/or ion (proton) strength (concentration) [
62]. This type of responsive property could be applied to nanofluidic devices (diodes) to rectify the transport of ions [
63]. The surfaces of the nano cannels also have been functionalized by metal oxides [
64], and the functionalized nanopores by thermo-responsive molecules have also been demonstrated as ion pumping channels [
65]. The morphological change induced by “nano holes” is also crucial to control the surface properties of the membranes, for instance, the precise modulation of the optical reflectance could be obtained [
66].
All these applications of the latent tracks given by the high energy charged particles are based on “damages” of molecular materials, and only few reports are on the materials fabrication such as target polymers/molecular materials. In many cases, physical/chemical properties of the latent tracks are missed and utilized simply as a platform for chemical reactions, leads to the formation of nanomaterials in the templated surface. The question is whether it is possible to produce nanomaterials confined in a nanospace of a particle track, retaining the physico-chemical properties of the target organic substances. The value of
S of a high energy heavy charged particle often reaches up to 3–4 orders of magnitude higher than the conventional γ-rays and high energy electrons in organic substances with a typical gravitational density of 1 g cm
−3, but considering the efficiency of chemical reactions represented by
G-values [
67], the overall yield of chemical reactions is still insufficient to cause dynamic changes to the properties of molecular materials. This is the answer for the question that was initial encountered for radiation effecting the matter. Polymeric materials with long linear chain like structures exhibit exceptional physical/mechanical properties, known as “plastics”, and especially the rheological properties depend strongly on the chain length both in solutions and condensed phases [
68]. Excellent theoretical formulations on the properties of polymeric materials have been successfully developed by Flory [
69], deGenne [
70,
71], etc., suggesting the feasibility of a limited number of crosslinks/chain scissions in an isolated particle track, leading to nanomaterials formation along the particle trajectory [
72].
To date, lithographic techniques are the primary choice to fabricate nanostructures based on organic substances, and most of the semiconductor devices are now patterned by replicating the structure of thin organic layers (resist materials in micro-nano lithography) where the nano-structures are formed via photo- or radiation- induced reactions in the layer [
73]. In this context, the most important factor is the determining the size and its accuracy to generate patterns by the intensive deposition of the released energy from incident photons/particles, and precision optics and focusing systems are indispensable to confine the chemical reaction into nm-sized spaces. However, the intra-track reactions based on the released energy from an isolated single particle provides intrinsically an ultimate limit of the “intensive deposition” into real nm-sized cylindrical spaces, without using any optics and focusing systems.
The sizes of a particle track are defined precisely by the theoretically derived value of
for an incident particle with certain kinetic energy, and the dissipation process occur by knocking out electrons through ionization events [
74,
75,
76,
77]. Here, we start from the equipartition theorem of energy released from a charged particle given by Equations (30) and (35), showing the inelastic collision processes, which can be divided into two kinds of collisions: indirect (ionizing) and direct energy transfer processes. The later are often referred to as “knock-on” collision events, in contrast to the Columbic force mediated interactions between the charges of an incident particle and electrons in the target media, which result in knocked-out secondary electrons, which is referred as “glancing” collision events. Here, the value of
is dissipated equally to the processes, and the size of “knock-on” collision depends only on the velocity of an incident charged particle, defined as
. The upper limit (
) of the size of the “glancing” collision can be given by the highest energy of knocked-out electrons. The spatial distributions are presumed to be constant for the former, and obey a conventional inverse square law for the letter as,
and
where
and
are the distribution function of the released energy in two area, often called as “core” and “penumbra(halo)” areas. Evidently, the former is far higher than the latter in the orders, and typically
~a few nm or less. The range of secondary electrons is 2–3 orders of magnitude larger than
, however for high energy heavy charged particles in non-relativity energy range, the value of
~100 nm at the largest. In solid phase of organic substances, limited diffusive motion of chemical intermediates secure their spatial distribution roughly proportional to the initial energy distribution represented particularly Equation (39): and this is the largest limit of the sizes of reaction field, which is also suggestive of the field well confined into nm-sized cylindrical area.
In order to cause a significant mechanical/rheological change of polymeric materials within the area, it is necessary to estimate the criterion for the density of chemical reactions (chemical core). Assuming cross-linking reactions as a key to immobilize the molecules in the chemical core and produce nanogels, we can easily calculate the required density of energy to produce sufficient crosslinks for polymer gelation based on the value of crosslinking efficiency;
. Generally, for gel formation in a polymer system, it is necessary to introduce one crosslink per polymer molecule. Assuming a sole contribution from the crosslinking reactions in the chemical core, the threshold density of
is given by,
where
,
d,
, and
are Avogadro’s number, gravitational density of polymer solids, mass of monomer unit, and the degree of polymerization, respectively. By substituting
in Equation (39) with
gives the following requirement for
r as [
78],
This gives a clear estimate of the chemical core size. If we employ a heavy particle with ~4000 eV nm−1 and chose the polymer target with ~0.1 (100 eV)−1, ~10000 g mol−1, Equation (41) leads to an estimate of r as ~5 nm, which is competitive or even smaller than the typical sizes of nanostructures fabricated by present lithographic techniques. The sizes of the nanostructures fabricated by the present scheme, SPNT, are discussed quantitatively based on this theoretical aspect.
Crosslinking reactions confined in the above cylindrical area were successfully visualized for polysilanes upon irradiation to MeV order charged particles. The visualization could be done in the following simple steps: (1) irradiation of thin solid films of polysilanes of ~1-μm thickness where the energy loss of incident particle is negligible to the initial kinetic energy, (2) immersing in the solvent which can dissolve the polymers prior to crosslinking reactions, and (3) visualization by the cylindrical crosslinked nano-gels by atomic force microscopy (AFM). The images obtained by AFM are shown in
Figure 1. The thickness of the nanowires changed significantly by the modulation of
of incident charged particles, which is clearly shown in the dependence of
on
as summarized in
Table 1.
Fine patterns of chemical cores in the AFM micrographs reveal clear 1D rod-like structures (nanowires) on the substrate. It should be noted that the density of the nanowires on the substrate increased clearly with an increase in the number of the incident particles, and the observed number density of the nanowires coincided with the number density of the incident particle. This is also suggestive that “one nanowire” is produced, corresponding incident particle along its trajectory, which is a clear evidence of the model described above. The length of the nanowires is uniform in each image, and is consistent precisely with the initial thickness of the film. This is due to the geometrical limitation of the distribution of crosslinking reaction: the gelation occurs from the top-surface to bottom of the polymer film. Thus, the length of the nanowires can be perfectly controlled by the present technique. Based on the measurement of cross-sectional trace of the nanowires by AFM, the radial distribution of crosslinks in the nanowires is discussed in terms of , defined as the radius of the cross-section. This strongly supports the hypothesis of theoretical Equation (41), where the value of is determined primarily by the molecular weight of the target polymer, the values of , and .
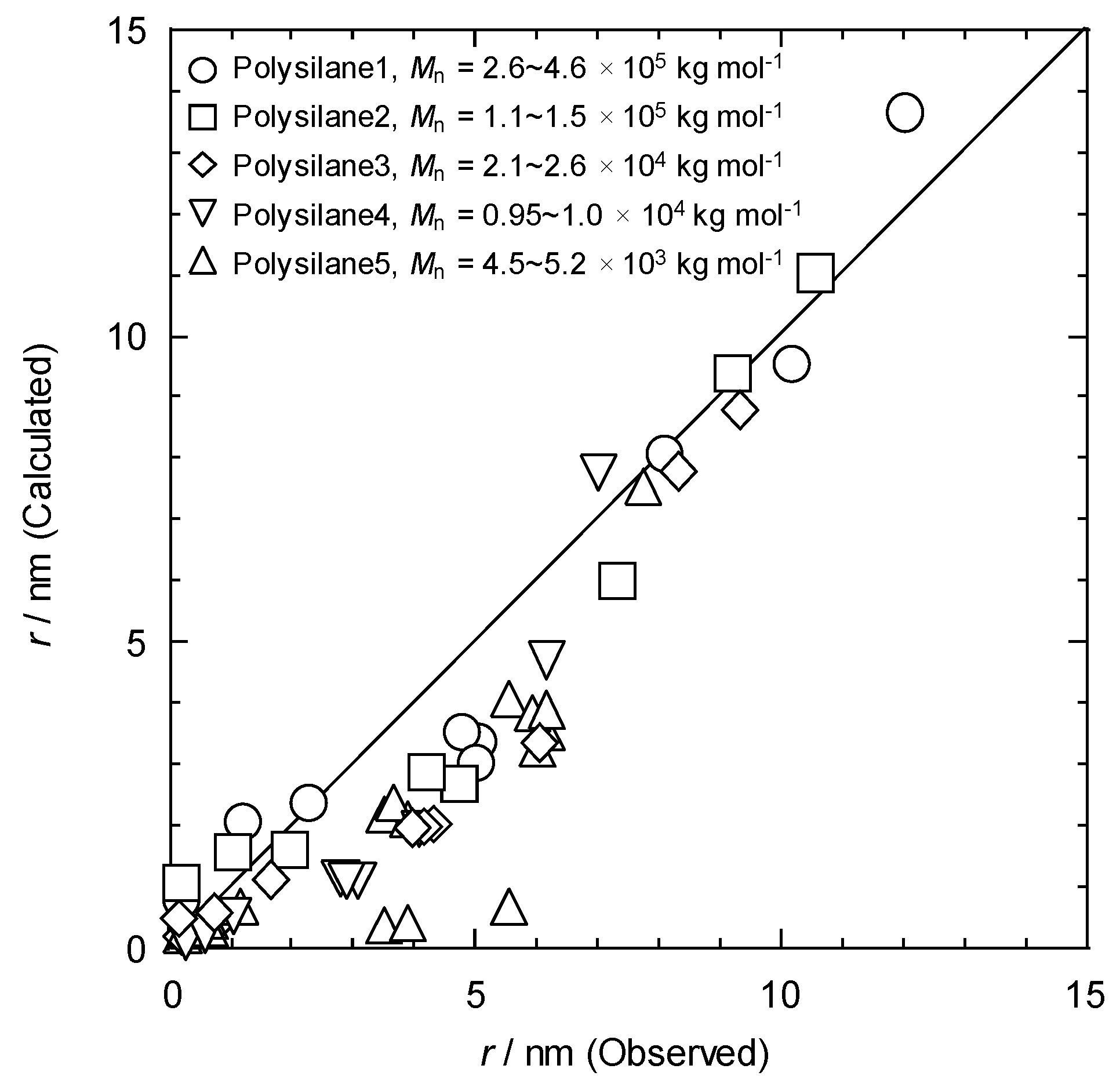
Upon extension of the SPNT to a wider range of polymeric systems with a variety of backbone structures, some discrepancy was found between predicted and measured values of r respectively by Equation (41) and the direct AFM traces. For instance in case of polysilane, using the reported value of = 0.12 derived from radiation-induced changes in molecular weight, the values of calculated by Equation (41) were compared with the experimental values, showing a good consistency with the experimental values for polymers with sufficient chain length ( > 104 kg mol−1). However, a considerable discrepancy occurs between the calculated and experimental results for the polymer with shorter chain lengths.
The global configuration of the polymers depends heavily on the length of the polymer chains, leading to transformation from random coil (long chain) to rod-like (short chain) conformations. The gyration radius of a polymers, which determines the size of a polymer spreading in the media, is correlated with this transformation. The correlation function between
Rg and
is provided by the well-established Flory–Huggins theory [
80] as given in the following simple form,
where
is the Flory–Huggins parameter,
is the molecular weight of the polymer, and
. Based on the persistence length of the target polymer materials, the scaling law for a helical worm-like chain model results directly in an index α from Equation (42). Thus, the effective volume of a polymer chain can be simply calculated as
, and the substitution of
in Equation (41) with the effective volume leads the next final expression [
78],
where
is the effective density parameter of the monomer unit (kg m
−3). Based on Equation (43), the calculated value of
is plotted again the experimental values in
Figure 2.
All the polymers with different molecular weights, follow a linear trend, and the calculated values display good correspondence in the range > 7 nm. The underestimated values of by Equation (42) for < 7 nm suggests that the initial deposition of energy and the radial dose distribution estimated by Equation (39), which do not account for the radial distribution of chemical intermediates and thus cannot model the concentration of crosslinking in the core of the ion track. The value of increases dramatically with an increase in the density of reactive intermediates. Based on the assumption that is a function of the density of deposited energy, the present results indicate that the yield of the chemical reaction is dependent on the energy density. Cross-linking reactions in ion tracks therefore have potential for not only single particle fabrication with sub-nanometer-scale spatial resolution for any kind of cross-linking polymer, but also the study of nanoscale distributions of radial dose and chemical yield in an ion track.
The successful fit between the experimental values and Equation (42) is not perfectly matched since the values of r were determined experimentally in air by tracing the morphology of the nanowire surfaces by a scanning probe microscope, while the Equation (42) was derived directly from the solution-based theory of polymer backbone conformations represented by Equation (41). The deviation of the measured radii from the theoretical predictions stems from the theoretically neglected nanowires–solvent interactions during the isolation of the nanowires from the non-irradiated polymer. The so-called “development” isolation was carried out by the washing out of non-crosslinked polymer materials by a “rich” solvent that interacts not only with the pristine polymer, but also to the nanowires themselves. The nanowires also interact strongly with the surfaces during these procedures and the subsequent drying processes, and this is a case of the “memorized” shape of macromolecules in solution even at the air-substrate interfaces. The dominance of crosslinking reaction upon irradiation to the charged particle is the only prerequisite for the polymeric materials to give nanowires via intra-track reactions by SPNT. This simple requirement presents us with an extremely wide range of applicability of SPNT to construct 1D nanostructure formation based on a variety of polymeric materials.
2.1. 1D Nanostructures Based on a Variety of Polymers
SPNT is applicable to various synthetic polymers other than polysilanes. The key to afford insoluble 1D nanostructures is to realize sufficient crosslinking reaction efficiency,
, that is mostly determined by chemical structures of polymers and energy/species of heavy ions. For example, polystyrene derivatives were extensively studied, and the formation of clear nanowires were confirmed after the development with aliphatic or aromatic hydrocarbon solvents [
81,
82]. Halogenated derivatives, poly(4-chlorostyrene) and poly(4-bromostyrene), were also irradiated with
129Xe ion beams, giving thicker nanowires with larger cross-sectional diameters [
83,
84]. The possible reason for the increase in diameters of nanowires resulted not only from the molecular weight of initial polymers, but also the dissociative electron attachment reactions often observed for halogenated hydrocarbons [
85,
86]. Reactive chemical species such as radicals are generated with a higher rate, because the nucleophilic attack of secondary electrons to a halogenated core to release a halide ion and leave neutral radical. In the classical radiation chemical processes, one of the typical primary processes to lead stable neutral radicals is the dehalogenation reaction through electron dissociative attachments. This process could be implemented to a substituent of the representative crosslinking type polymers: poly(chlorostyrene)s. Upon irradiation with high energy charged particles, significant jump in the yield of neutral radicals was observed as well as the dehydrogenation reaction of α protons, resulting in increase in both of crosslinking efficiency and of the cross-sectional diameter. Conjugated polymers such as polyaniline (PANi) and poly(3-hexylthiophene) (P3HT) were also studied as starting materials for SPNT [
87], where the absorption and photoluminescent spectra of the resulting nanowires are similar to those of the starting polymer films.
The capability of post-functionalization and post-treatment of nanowires is worth noting for the extension of the SPNT protocol. Polycarbosilane (PCS) is known as a precursor polymer for silicon carbide (SiC), a material with high mechanical properties and thermal conductivity, having chemical stability. Mechanical properties can be strengthened through the fiber-reinforced composite ceramics. To access fibrous SiC from PCS precursors, SPNT and following calcination process was demonstrated [
88]. PCS nanowires were fabricated by 450 MeV
129Xe beam irradiation to afford uniform nanowires with controlled number density. Then, pyrolysis was performed at 1000 °C under Ar atmosphere, resulting in SiC with the shrinkage of the nanowires. Considering the densities of PCS and SiC, the observed shrinkage of 33%–44% is reasonable for the conversion from PCS to SiC nanowires. XRD analysis of the nanowires supported the formation of both α and β phases of SiC, which suggests the structural difference between core and penumbra regions.
Another feature of SPNT include block-
co-nanowire formation by simply applying SPNT to multilayer films. By using hydrophobic/hydrophilic multilayer polymer films, the morphology control of segmented nanowires was reported [
89]. In this work, PCS and poly(methylphenylsilane) (PMPS) were chosen as hydrophobic polymers while poly(hydroxystyrene) (PHS) was used as a hydrophilic one. PCS and PMPS are soluble in toluene but insoluble in isopropylalcohol (IPA), while PHS has the opposite solubility. This orthogonal solubility enables the preparation of multilayer films by a simple spin-coating method without affecting lower layers. PCS-PHS-PMPS films were irradiated with heavy ions and developed with toluene/IPA (2/1 v/v) mixtures. AFM observation disclosed that the obtained nanostructures adopt unique octopus-like morphology, where the central PHS segments selectively aggregate among adjacent nanowires (
Figure 3). It is suggested that the bindings of the different polymer segments at their interfaces play an important role in the tangling of hydrophilic polymer segments with stretched hydrophobic polymer legs. The heteromolecular cross-linking reactions at the interfaces of PHS/PCS or PHS/PMPS would be key for the bindings of the multi-segment nanowires.
2.2. 1D Nanostructures Responsive to External Stimuli
If the starting polymers exhibit changes in conformation upon applying the external stimulus (thermal- or photo- induced stimuli), the corresponding nanowires developed by SPNT should retain such responsiveness that can be visualized by microscopies as a nanoscale event. Poly(
N-isopropylacrylamide) (PNIPAAm) is a famous thermoresponsive polymer having a lower critical solution temperature (LCST). This polymer is hydrated and swelled below 32 °C, but shrinks and finally segregated over that temperature by releasing the water molecules. The temperature-responsive swelling–shrinking behavior was clearly visualized in the form of nanowires. Although pure PNIPAAm films failed to form nanowires via 490 MeV
192Os
30+ ion beam and following development with IPA, the thick nanowires were successfully obtained from a hybrid film of PNIPAAm/
N,
N′-methylene-bis-acrylamide (MBAAm) cross-linker (100/20 wt/wt) [
90]. After the resultant nanowires on substrates are placed in water at controlled temperatures, the nanowires shrank under the conditions of 40 and 50 °C, whereas no distinct change was observed at 25 °C in water (
Figure 4). From a more quantitative aspect, the increase in cross-sectional diameter and decrease in length were revealed in the PNIPAAm/MBAAm nanowire system. Nanowires fabricated by SPNT are insoluble nano-size gels. This work showed the temperature responsiveness of PNIPAM is preserved in the nanogel form. The temperature responsive was further controlled in a reversible way by PNIPAAm–poly(vinylpyrrolidone) (PVP) block nanowires where the latter as an internal standard [
91]. Irresponsive nature of PVP segments against temperature modulation gave a clear contrast to the morphological changes of PNIPAAm segments, and the changes induced by LCST of the base polymer: PNIPAAm were confirmed to demonstrate high reversibility under the sequential cycles of temperature modulation. This is suggestive of the future application of the present combined nanowires acting as stimuli-responsive containers such as drug carriers.
Photoresponsive properties were also imparted into nanowires by incorporating azobenzene moieties into the target polymers [
92]. Azobenzene is a representative molecule undergoing a reversible photo-isomerization between its -
cis and -
trans isomers. Random copolymers of 9,9′-dioctylfluorene and 4,4′-azobenzene were prepared by Suzuki cross-coupling reactions. The electronic absorption spectral changes upon 401 nm light exposure were confirmed for the condensed phase. The copolymer films were successfully converted to nanowires by SPNT, and their photoresponsive property was directly investigated by morphological trace. Upon
trans-to-
cis isomerization, a clear transformation from a straight to wavy morphology was visualized, associated with an enhancement of roughness of the surface. Simultaneously, end-to-end distance of the nanowires increased with photoisomerization into
cis-form. This implies that the microscopic isomerization in a molecular level could be reflected and scaled into the statistical changes of global configurations of the nanowires.
2.3. 1D Nanostructures with Optoelectronic Activities
The cross-sectional sizes of nanowires given by SPNT are ranging from few nm to …, suggesting their possible application as electronic conductive wires and/or platforms for quantum confinements of elemental excitation energies. The electrical conductivity of an isolated nanowire was measured by nano-gap devices with Pt electrodes [
93]. Note that the electrodes were fabricated by a conventional electron-beam assisted lithographic technique followed by the vacuum deposition of Pt and lifting-off of resist materials used, and the nanowires produced by crosslinking reactions in polysilanes showed high enough tolerance for all the above processes, as seen in
Figure 5. Current-voltage measurements of the nanowires bridged between the electrodes showed clearly the semi conductive nature of charge carriers, and a potential as electronic conductive nanowires.
The interplay of electronic and optical properties in isolated nanowires was examined for a series of conjugated polymers as the targets. Reflecting efficient radiative/non-radiative energy dissipation processes through the higher density of states in conjugated polymer main chains, the efficiency of main chain scission reactions is often suppressed, and surpassed by side chain crosslinking reactions. All conjugated polymers examined, namely Poly(9,9′-di-n-octylfluorene) (PFO), regioregular poly(3-hexylthiophene) (rrP3HT), and poly[2-methoxy-5-(2′-ethylhexyloxy)-ethylhexyloxy)-1,4-phenylenevinylene] (MEH-PPV), gave successfully corresponding nanowires with a high aspect ratio of ~200, suggesting high enough mechanical strength without fragmentation during isolation (development) processes by solvents with high affinity for the initial polymer materials [
94]. Particularly PFO-based nanowires exhibited clear signature of fluorescence from singlet excited state of PFO backbone conjugated systems with remarkably high quantum efficiency which was still observable for isolated nanowires on the substrates. The high quantum efficiency is also suggestive of disappearance of bulk quenching pathways for the excited states which had been often observed in condensed phase of luminescent organic materials.
“Intra-nanowire” Förster resonance energy transfer (FRET) from the energy harvesting nanowire body to tetramethylrhodamine (TAMRA) was demonstrated using fluorescent nanowires based on poly(9,9′-dialkylfluorene)s [
95]. Random copolymers of (9,9′-dioctylfluorene) and (9,9′-di(5-hexynyl)fluorene) carrying terminal alkyne groups was synthesized. After formation of nanowires by SPNT, blue fluorescence from polyfluorene backbone was confirmed. TAMRA was attached by post-functionalization of the terminal alkyne groups via “click” chemistry on the surface of nanowire. After TAMRA-functionalization, fluorescence from the nanowires was turned into red as evident from confocal fluorescence microscopy, which indicates efficient FRET from polyfluorene-based nanowire body to TAMRA as schematized in
Figure 6. Although this case reports the covalent conjugation between the nanowire surface and analyte (=TAMRA), the concept can be extended to the noncovalent interaction-based sensing systems with the extremely wide surface area of nanowires.
2.4. 1D Nanostructures from Biomacromolecules
Inspired by the successful formation of stimuli-responsive nanomaterials and facile combination/joint of nanowire segments, SPNT has been extended to bio-macromolecules towards the future diagnostic/therapeutic/medical application of the nanowires. The first example of bio-macromolecular nanowires was given based on proteins [
96].
Figure 7 shows bovine serum albumin-based nanowires isolated and visualized clearly by AFM. Crosslinking efficiency in protein molecules strongly depends on the composition/arrangement of amino acid in their chains, and albumin revealed to be an ideal platform to give nanowires through SPNT protocols. The length of the nanowires reached over 10 μm with extremely high aspect ratio of ~1000. The presumed high mechanical strength from the aspect ratio could be ascribed to the competitive/higher density of crosslinks in protein nanowires. The high inter- and intra-chain reactions of amino acids arranged in albumin, allowing us the further functionalization of the nanowire surfaces. The dense distribution of amine groups on the nanowire surfaces could be biotinylated, and through biotin-streptavidine interactions, a variety of biologically active groups can be decorated on the surface of nanowire. It is noteworthy to mention that protein nanowires were digested by enzymes such as trypsin, suggesting principally that the nanowires are composed of peptide linkages.
Facile surface modification of nanowires allows us to impart biocompatibility to nanowires of commercially available polymers with the higher mechanical and/or optoelectronic properties. For instance, the surface of polystyrene nanowires could be activated through copolymerization of styrene with ethynylstyrene as represented in
Figure 8, and grafting protocol using Click chemistry was applied to introduce terminal alkyne functional groups [
97]. Antigen–antibody interactions, as in the above case, were well demonstrated to decorate the nanowires surfaces by bio-compatible molecules and macromolecules, such as proteins.
Another challenging target is “sugar” to give nanowires by SPNT [
98]. As revealed previously, an efficient DNA damage can be done by radiations in cancer radio therapy. Polysaccharides suffer significantly from main chain scission reactions, which make it challenging to promote crosslinking reactions in these materials. The primary process of the reaction was known to be triggered by the deprotonation reaction of hydroxy groups in sugar molecules, thus methylated polysaccharides were employed and led into nanowires successfully. Although fragmentation occurred relatively in the higher ratio, this was due to the lower crosslinking density.
2.5. 1D Nanostructure Formation for Visualization of Ion Tracks
One of the major/most critical issues in SPNT is spatial resolution/position sensitivity of “single” particle competitive to the size of nanowires. As demonstrated in the dosimetry of galactic cosmic rays in
Section 2, the hitting position by a particle could be visualized clearly by subsequent chemical etching processes. However, the decomposition of the target organic substances simultaneously spoils the spatial resolution of an exact center of hitting position due to inhomogeneity/fluctuation of chemical reactions in the slow-wet processes. The direct visualization of the “latent” particle tracks was realized by a simple protocol: exposure to a humid environment soon after the irradiation of high energy charged particles [
99]. Intra-track chemical reactions caused dramatic changes in the diffusion constant for small molecules, and herein water molecules penetrating selectively in the latent track led to a significant volume expansion only in the latent track area. Morphological traces on the surface allows for the precise determination of the hitting position of each charge particle with less than a few nm spatial resolution.
3. Single Particle Triggered Linear Polymerization (STLiP): Facile and Universal Polymerization Confined into nm-scaled Area
Macromolecules become insoluble with several crosslinking points, which makes them advantageous as starting materials for SPNT. Also, polymer materials are beneficiary due to easy film-formation capability. In contrast, small molecular materials require not only crosslinking but also chain-like polymerization reactions in order to afford insoluble nanogels. In addition, small molecules often cause crystallization that is sometimes disadvantage for film preparation. However, by the recent examinations using particular molecular design and solvent for development, small molecular materials have now been suitable candidate for ion beam triggered nanostructure formation. The method using small molecules was distinguished from SPNT and thus named as “single particle triggered linear polymerization (STLiP)”.
Silsesquioxanes are small molecular analogues of polysiloxanes and have amorphous nature to yield smooth films by spin-coating. Films of two silsesquioxane derivatives were exposed to 450 MeV
129Xe beams, and uniform nanowires were obtained [
100]. By comparing the two derivatives, the derivative carrying vinyl termini resulted nanowires with a large cross-sectional radius (
= 10.1) than that of the hydroxy-terminated derivative (
= 7.0 nm). Therefore, vinyl groups may be the key to efficient radiation-induced chemical reactions [
83]. The information worth noting that includes the larger cross-sectional radius of the resultant nanowires from poly(silsesquioxanes) (
= 14.3 nm) than those from monomeric silsesquioxanes (
= 10.1 nm). This fact is reasonable, considering the size of the initial molecules.
Not only vinyl, but also other unsaturated bonds were found to be effective starting materials for STLiP method. Pentacene derivatives, 6,13-bis(triethylsilylethynyl)pentacene and 6,13-bis((triisopropylsilyl)ethynyl)pentacene were successfully converted to nanowires by the irradiation with 490 MeV
192Os and developed with
n-hexane [
101]. The absence of nanowires from simple pristine pentacene implied the importance of unsaturated bonds, inner alkyne groups. One of the ultimately unsaturated carbon allotropes is fullerene derivatives. In fact, polymerization of C
60 films by UV light [
102] or electron beam [
103], and their enhanced electrical conductivity [
104] were reported previously. Furthermore, intra-track polymerization was also achieved by irradiation with swift heavy ions at the fluence of 1 × 10
12 cm
−2 [
105]. Although isolation of polymerized carbon nanowires has not been done, the track-shaped 1D nanostructures were evidenced by conducting-mode AFM measurements [
106,
107,
108]. The isolation of fullerene derivatives nanowires was reported by Seki et al. [
109].
Figure 9 shows a clear rod-like shape of nanowire as well as high resolution image of a nanowire representing polymerized fullerene molecules by irradiation with high energy heavy ions. The fullerene-based nanowires were incorporated in the active layer of P3HT/PCBM in photovoltaic devices. The role of unsaturated carbon–carbon bonds on the efficient nanowire formation by swift heavy ion irradiations could be explained on the basis of bond energy. The bond energy of a C–H bond is higher than that of C–C, C=C, and C≡C bonds, and the cleavage of a C–H bond releases a hydrogen radical or proton that is soon removed from the system. On the other hand, the cleavage of a carbon–carbon bond generates reactive radical species capable of polymerizations. The absence of terminal C–H–– and the presence of unsaturated bond––may be the key for high reactivity upon irradiations. This hypothesis is related to the notion of hydrogen loss energy [
110].
Aromatic amines are the candidates for the starting materials of STLiP technique. Motivated by the easy radical cation formation of aromatic amines [
111], STLiP was demonstrated for amorphous solid films of a series of aromatic amines [
112]. The distribution of the cross-sectional radii of the nanowires is small that reflecting the size of the molecules, which is also discussed in the field of resist materials for lithography [
113]. Pristine nanowires were obtained by irradiation with high energy heavy ions and following solvent treatment with aliphatic hydrocarbon solvents such as hexane and cyclohexane. When the isolated nanowires were immersed in CHCl
3, time-dependent fragmentation of the nanowires were monitored (
Figure 10). This observation suggested that that the nanowires were formed not only by crosslinking (complete covalent bondings) but also by entanglement (multiple noncovalent interactions) of the polymerized products.
Further analyses from the mechanistic and quantitative aspects were performed by employing 9,9′-spirobi[9
H-fluorene] (SBF) and its brominated derivatives [
114]. Spin-coated films of SBF, 2-bromo-SBF (2Br-SBF), 4-bromo-SBF (4Br-SBF), 2,2′-dibromo-SBF (2,2′Br
2-SBF), 2,7-dibromo-SBF (2,7Br
2-SBF), 2,2′,7,7′-tetrabromo-SBF (Br
4-SBF), 2,2"-bi-9,9’-spirobi[9
H-fluorene] (SBF
2), and 2,2":7",2""-ter-9,9′-spirobi[9
H-fluorene] (SBF
3) were irradiated with 350 MeV
129Xe
26+ ions, and their nanowires were isolated after development with toluene.
Figure 11 shows a series of AFM micrographs visualizing the SBF-based nanowires with a variety of thickness and length, and apparently the thinner nanowires from SBF, 2,7Br
2-SBF, and 2Br-SBF suffered significant fragmentation during development processes under the strong solvent: toluene.
The values were evaluated by cross-sectional views in AFM, revealing the order of (SBF) < (SBF2) < (SBF3) and (SBF) < (2,7Br2-SBF) < (2Br-SBF) ~ (4Br-SBF) < (2,2′Br2-SBF) < (Br4-SBF). The order of the former can be interpreted as the effect of molecular size on the oligomerization/crosslinking reactions; the starting larger oligomers reach the polymerized products more easily. Larger observed in Br-substituted SBFs reflects the dissociative electron attachment of the generated secondary electrons to the halogenated compounds and preferential cleavage of C6H5–Br due to its smaller bond energy (~336 kJ mol−1) than that of C6H5–H (~472 kJ mol−1). This explanation is supported by X-ray photoelectron spectroscopy (XPS) measurements, suggesting a significant reduction of the photoelectron signals, and hence composition, of Br atoms in the nanowires.
Based on Equation (39), the energy density at the surface of nanowires (
) was calculated as summarized in
Table 2, by using the averaged cross-sectional radius of nanowires for each starting compound and the stopping power simulated by Monte-Carlo code (SRIM2008). The given energy per molecule around the nanowire surface (
) is also summarized in
Table 2. These values were calculated from
and molecular volumes estimated from the crystal structures of the SBF derivatives. Most likely at the nanowire surface, at least one chemical bond is formed to immobilize the molecule. The reported crystal structures denoted that one SBF molecule is surrounded by six nearest neighbor molecules capable of bond formation, and the SBF molecule at the nanowire surface should react with either of the three inner molecules, in order to immobilized to a nanowire. Consequently, the
values for bond formation with the inner nearest neighbors are roughly estimated to be in the range of 8.6–9.7 (100 eV)
−1 for the monomeric SBF derivatives in this irradiation condition, whereas the dimer and trimer yielded smaller
values of 5.4 and 3.9 (100 eV)
−1, respectively. These values are larger than that for the case of polymers, revealing efficient solid-state polymerization of the SBF derivatives upon high-energy particle irradiation. Although this analysis does not take account competitive bond cleavages by irradiations, the solid-state intra-track polymerization reaction efficiency,
, was estimated for the first time to address the feasibility of organic molecules for the STLiP technique, leading to corresponding 1-D nanomaterials.
Sublimation is one of the remarkable characters for small molecules. The nanowires fabricated via SPNT or STLiP are always isolated by the development process. Development with organic solvents is an easy method that accelerates the throughput of various nanowires from variety of materials. At the same time, the isolated nanowires are always parallel to substrates due to the tensile force of solvent liquid and irreversible adhesion to the substrate. As an orthogonal isolation process toward development, sublimation has been tried recently. For example, vapor-deposited smooth films of C
60 were irradiated with high energy heavy ions at relatively high fluence (>10
11 cm
−2) to form nanowires perpendicular to the substrate. When the film was developed with 1,2-dichlorobenzene, bundled nanowires were lying down to the substrate. In contrast, subsequent sublimation after irradiation afforded a different morphology. AFM measurements unveiled that the C
60-based nanowires were vertically oriented to the substrate, and the length of the nanowires correspond to the initial thickness of the films (
Figure 12). The sublimation process is an alternative way to development, which opens another possibility for the orientation control of the nanowires developed by STLiP.