Time-Of-Flight ERDA for Depth Profiling of Light Elements
Abstract
:1. Introduction
2. Principle of ERDA
3. Principle and Measurement System of the TOF-ERDA
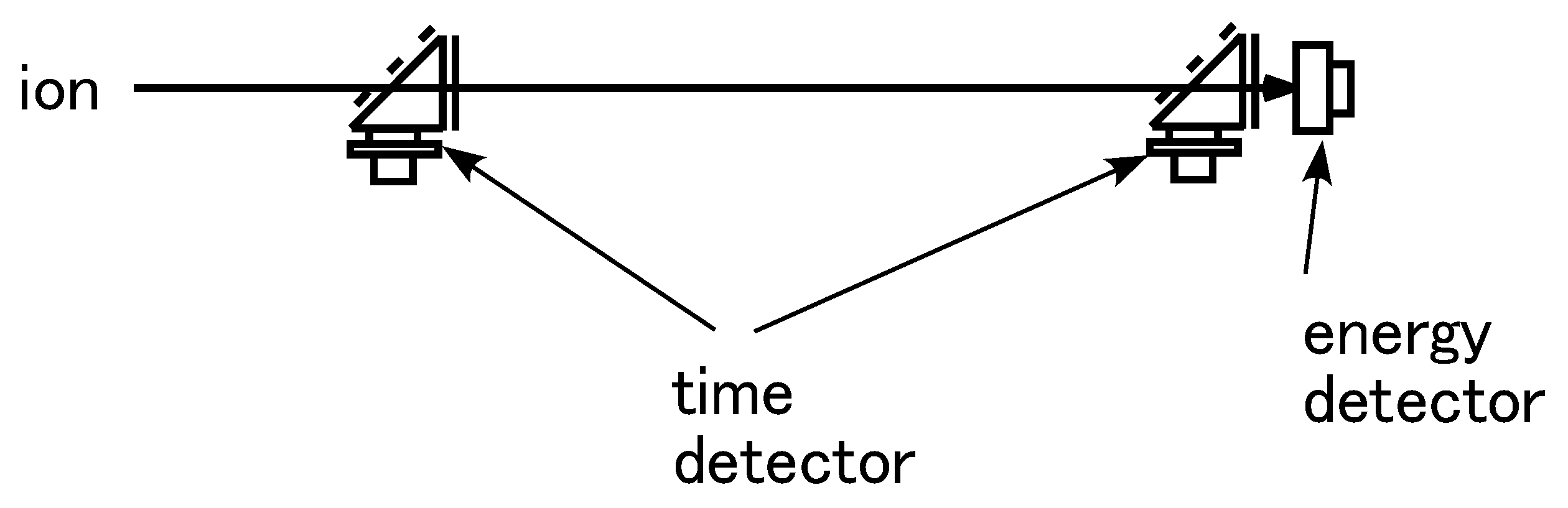
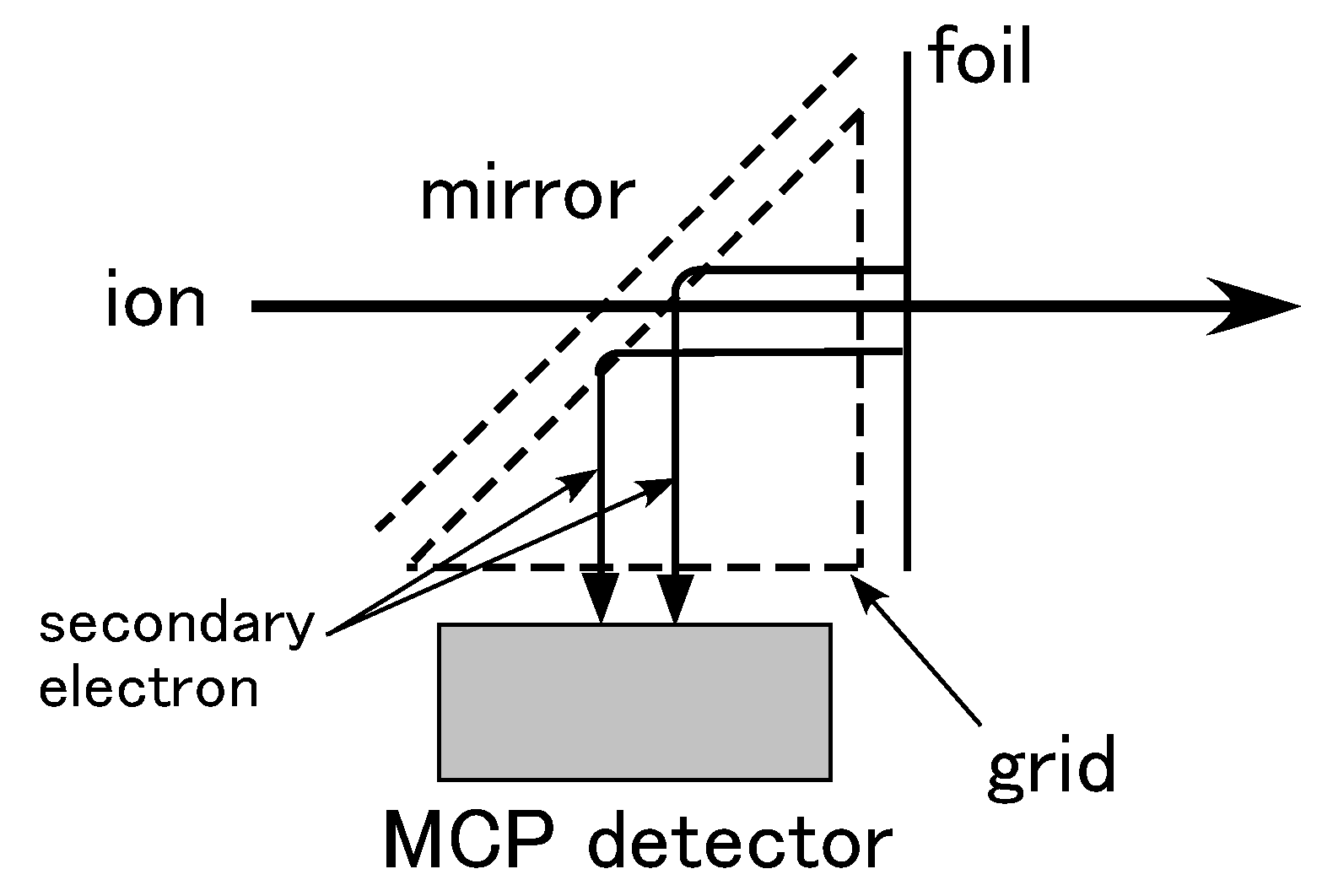
3.1. Overview
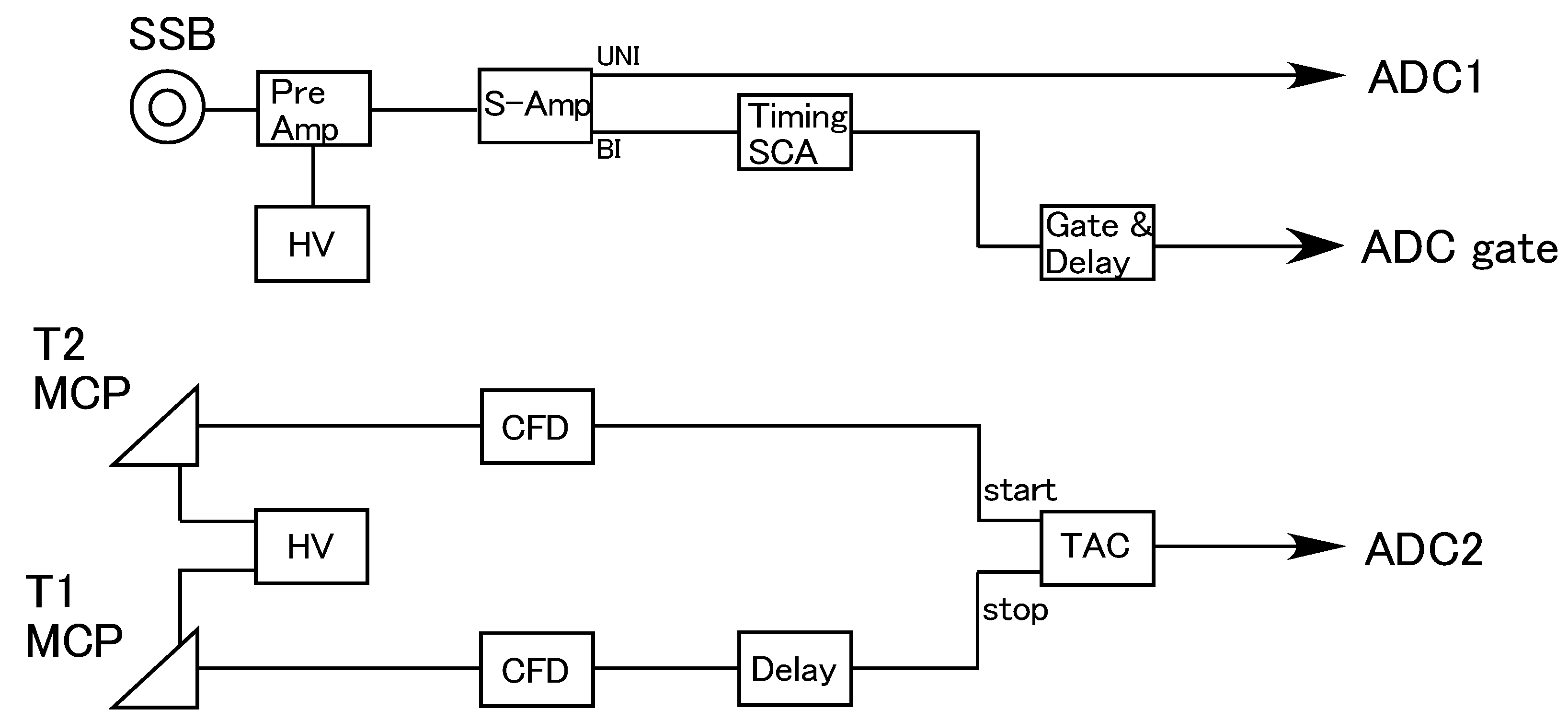
3.2. Measurement Set-Up
4. System Performance
4.1. Time Resolution
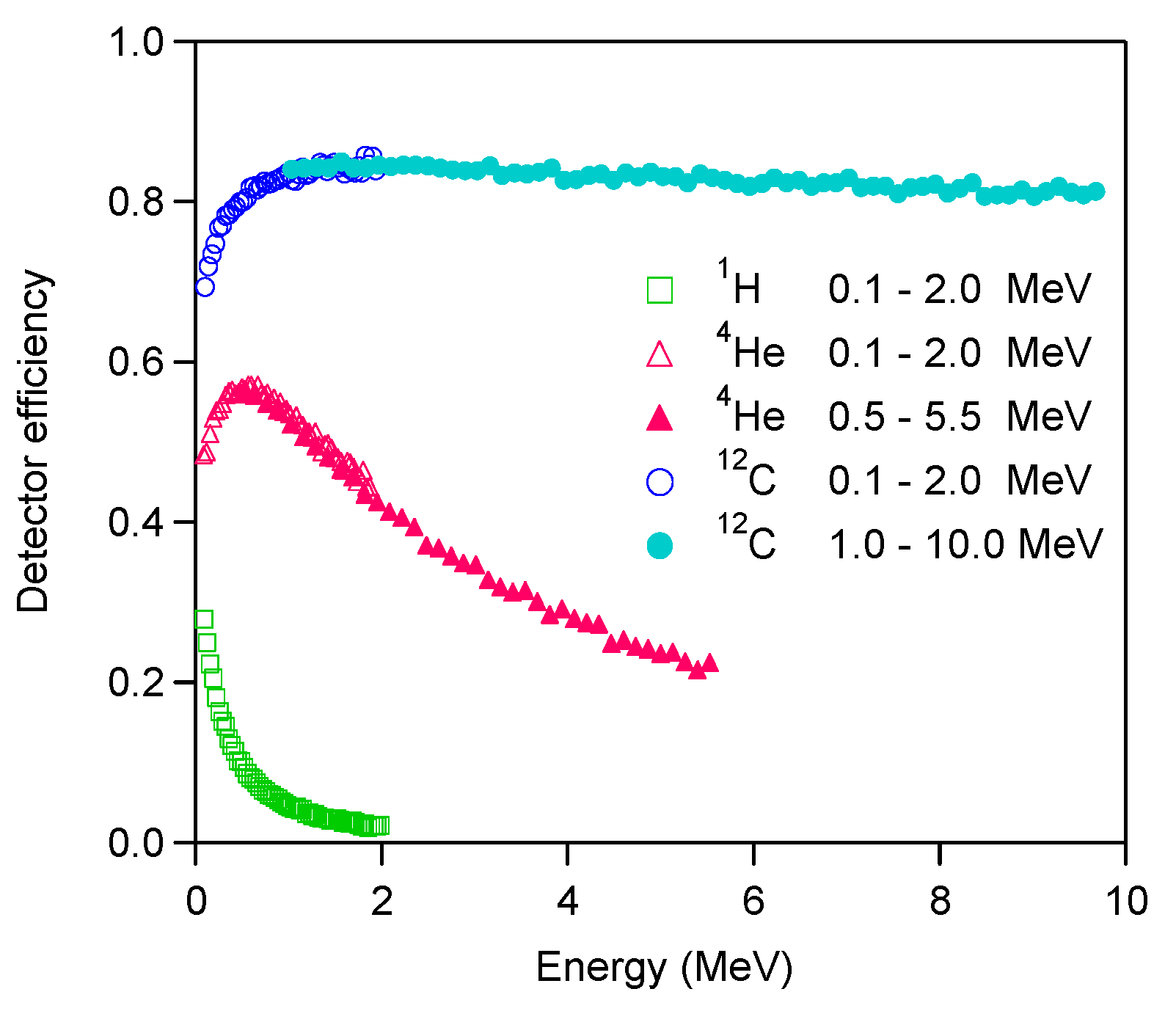
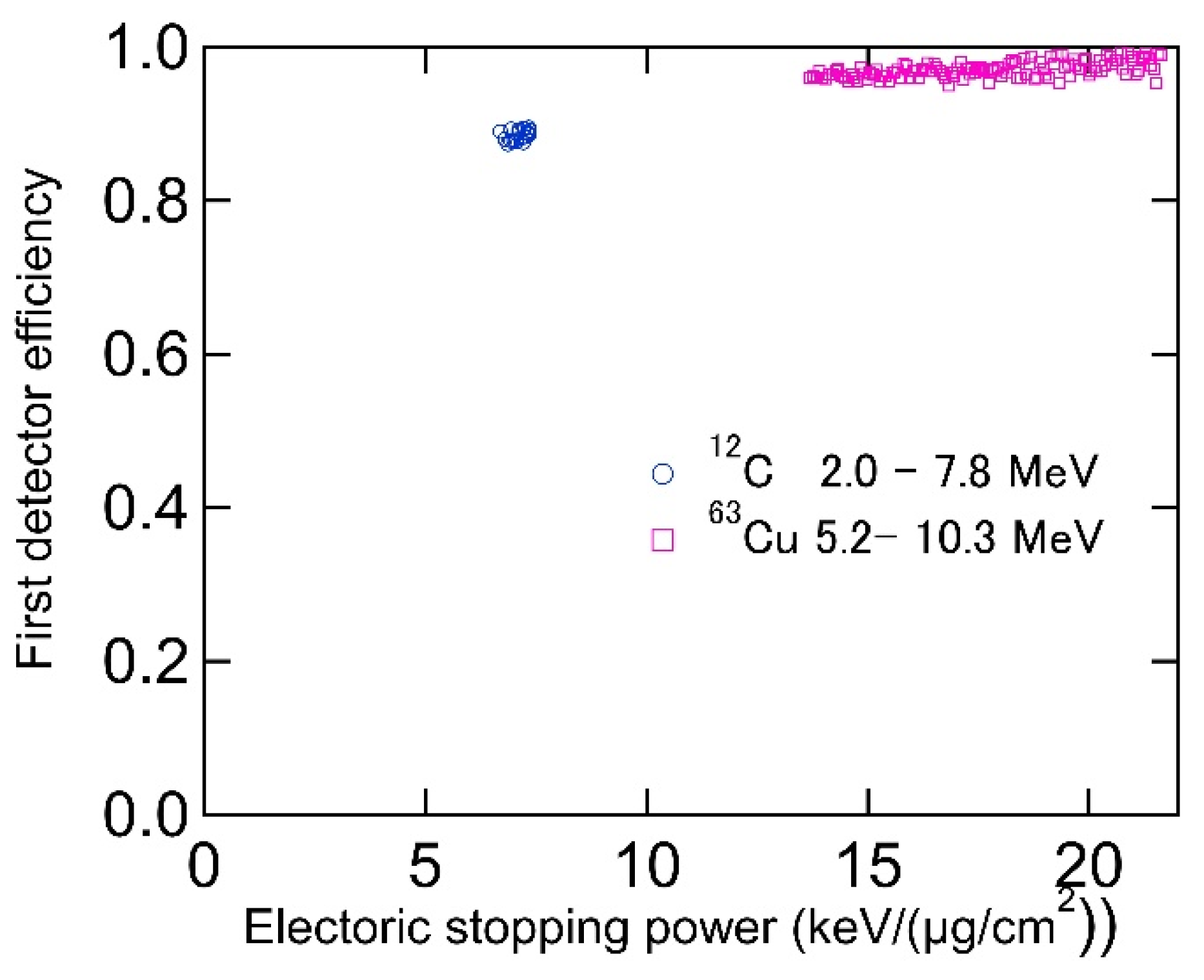
4.2. Detection Efficiency
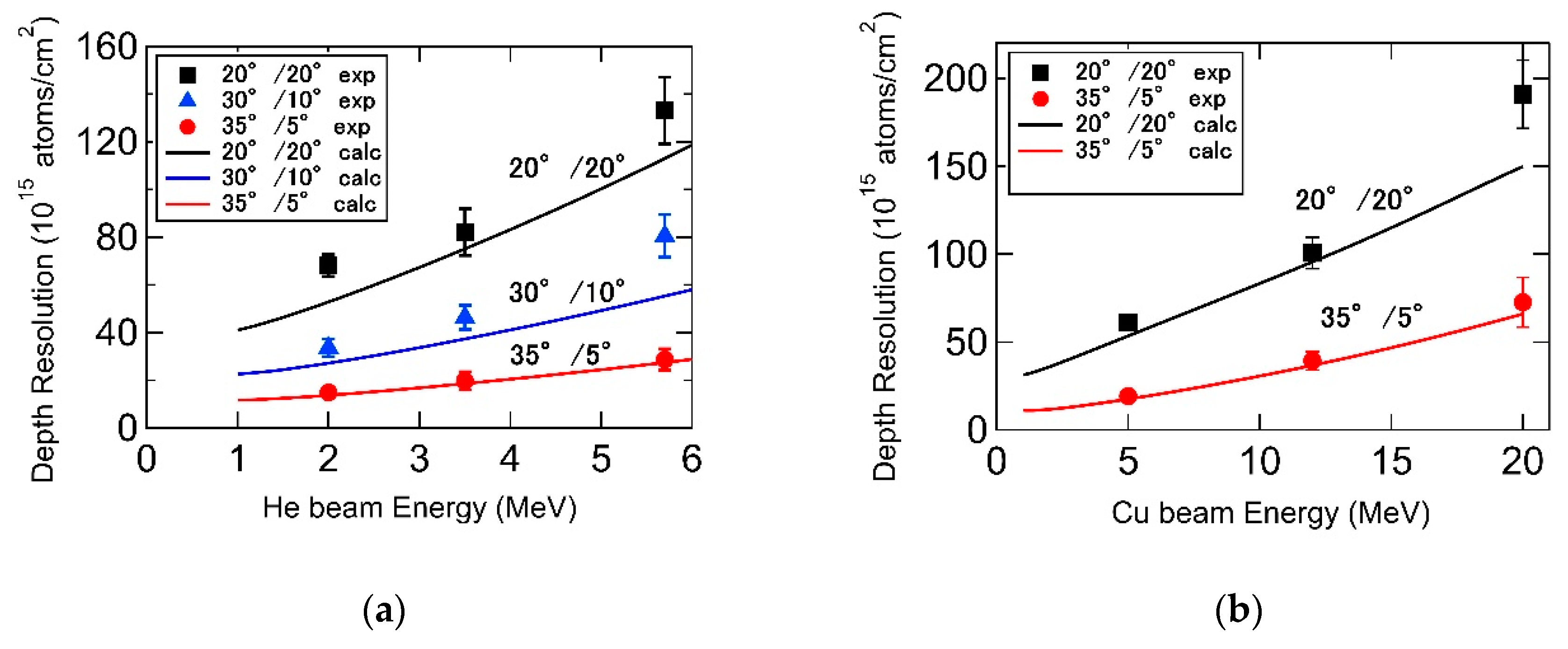
4.3. Depth Resolution
4.4. Sensitivity
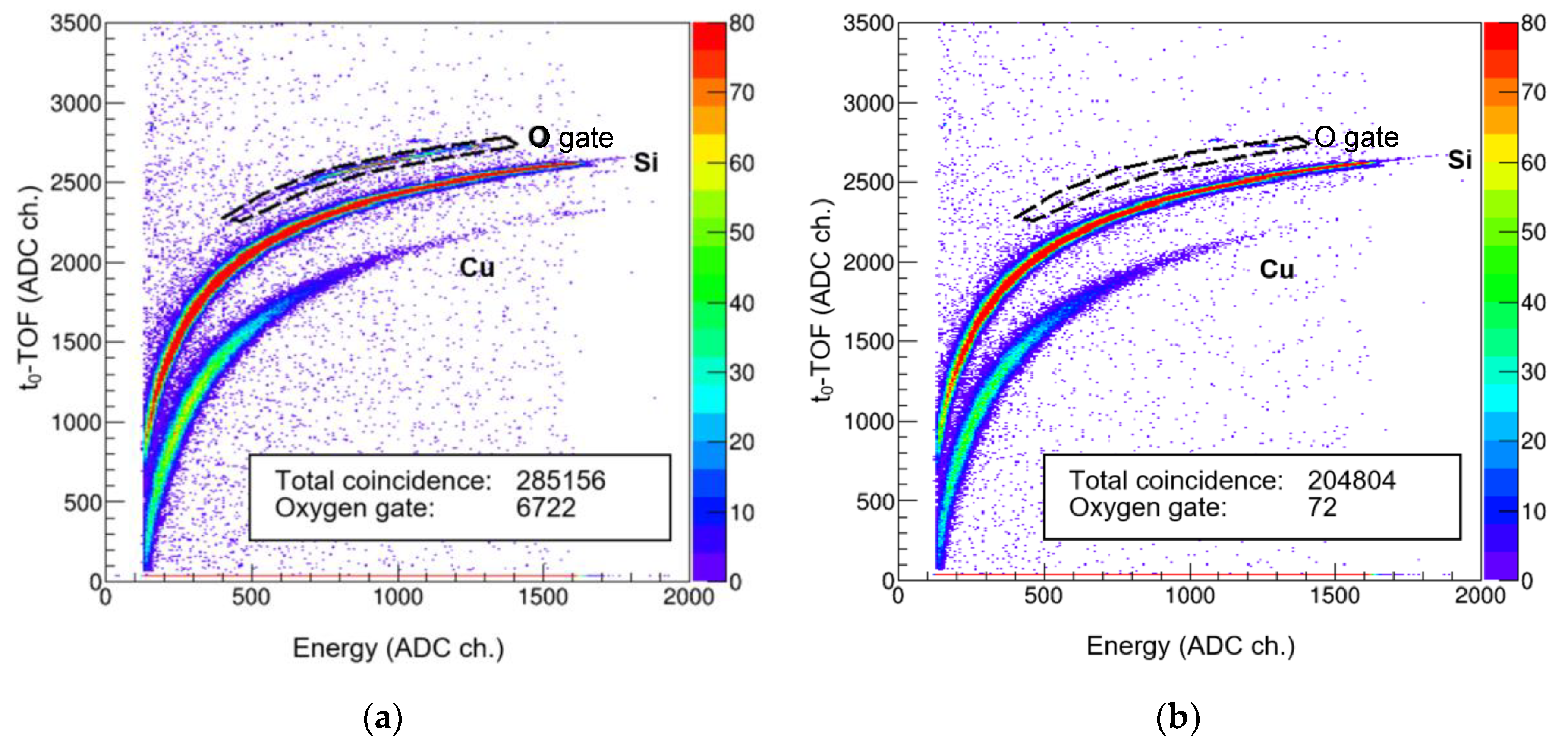
5. Example
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Robertson, J. High dielectric constant gate oxides for metal oxide Si transistors. Rep. Prog. Phys. 2005, 69, 327. [Google Scholar] [CrossRef]
- Gusev, E.P.; Cartier, E.; Buchanan, D.A.; Gribelyuk, M.; Copel, M.; Okorn-Schmidt, H.; D’Emic, C. Ultrathin high-K metal oxides on silicon: Processing, characterization and integration issues. Microelectron. Eng. 2001, 59, 341–349. [Google Scholar] [CrossRef]
- Wang, Y.; Nastasi, M. Handbook of Modern Ion Beam Materials Analysis; MRS: Warredale, PA, USA, 2009. [Google Scholar]
- Kottler, C.; Döbeli, M.; Glaus, F.; Suter, M. A spectrometer for low energy heavy ion ERDA. Nucl. Instrum. Methods Phys. Res. Sect. B 2006, 248, 155–162. [Google Scholar] [CrossRef]
- Siketić, Z.; Radović, I.B.; Jakšić, M. Development of a time-of-flight spectrometer at the Ruder Bošković Institute in Zagreb. Nucl. Instrum. Methods Phys. Res. Sect. B 2008, 266, 1328–1332. [Google Scholar] [CrossRef]
- Giangrandi, S.; Sajavaara, T.; Brijs, B.; Arstila, K.; Vantomme, A.; Vandervorst, W. Low-energy heavy-ion TOF-ERDA setup for quantitative depth profiling of thin film. Nucl. Instrum. Methods Phys. Res. Sect. B 2008, 266, 5144–5150. [Google Scholar] [CrossRef]
- Msimanga, M.; Wamwangi, D.; Comrie, C.M.; Pineda-Vargas, C.A.; Nkosi, M.; Hlatshwayo, T. A Time of Flight-Energy spectrometer for stopping power measurements in Heavy lon-ERD analysis at iThemba LABS. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 2671–2674. [Google Scholar] [CrossRef]
- Laitinen, M.; Rossi, M.; Julin, J.; Sajavaara, T. Time-of-flight—Energy spectrometer for elemental depth profiling—Jyväskylä design. Nucl. Instrum. Methods Phys. Res. Sect. B 2014, 337, 55–61. [Google Scholar] [CrossRef] [Green Version]
- Chicoine, M.; Schiettekatte, F.; Laitinen, M.I.; Sajavaara, T. Oxy-nitrides characterization with a new ERD-TOF system. Nucl. Instrum. Methods Phys. Res. Sect. B 2017, 406, 112–114. [Google Scholar] [CrossRef]
- L’Ecuyer, J.; Brassard, C.; Cardinal, C.; Chabbal, J.; Deschênes, L.; Labrie, J.P.; Terreault, B.; Martel, J.G.; St.-Jacques, R.J. An accurate and sensitive method for the determination of the depth distribution of light elements in heavy materials. Appl. Phys. 1976, 47, 381–382. [Google Scholar]
- Doyle, B.L.; Peercy, P.S. Technique for profiling 1H with 2.5-MeV Van de Graaff accelerators. App. Phys. Lett. 1979, 34, 811–813. [Google Scholar] [CrossRef]
- SRIM2008. Available online: http://www.srim.org (accessed on 17 November 2020).
- IBANDL. Available online: https://www-nds.iaea.org/exfor/ibandl.htm (accessed on 17 November 2020).
- SigmaCalc. Available online: http://sigmacalc.iate.obninsk.ru (accessed on 17 November 2020).
- Gurbich, A.F. SigmaCalc recent development and present status of the evaluated cross-sections for IBA. Nucl. Instrum. Methods Phys. Res. Sect. B 2016, 371, 27–32. [Google Scholar] [CrossRef]
- Pászti, F.; Szilágyi, E.; Kótai, E. Optimization of the depth resolution in elastic recoil detection. Nucl. Instrum. Methods Phys. Res. Sect. B 1991, 54, 507–512. [Google Scholar] [CrossRef]
- Razpet, A.; Pelicon, P.; Rupnik, Z.; Budnar, M. Development of a time-of-flight telescope for ERDA at the Jožef Stefan Institute. Nucl. Instrum. Methods Phys. Res. Sect. B 2003, 201, 535–542. [Google Scholar] [CrossRef]
- Hong, W.; Hayakawa, S.; Maeda, K.; Fukuda, S.; Yanokura, M.; Aratani, M.; Kimura, K.; Gohshi, Y.; Tanihata, I. Development of a high mass-resolution TOF-ERDA system for a wide mass range. Nucl. Instrum. Methods Phys. Res. Sect. B 1997, 124, 95–99. [Google Scholar] [CrossRef]
- Busch, F.; Pfeffer, W.; Kohlmeyer, B.; Schull, D.; Puhlhoffer, F. A position-sensitive transmission time detector. Nucl. Instrum. Methods 1980, 171, 71–74. [Google Scholar] [CrossRef]
- Döbeli, M.; Kottler, C.; Stocker, M.; Weinmann, S.; Synal, H.-A.; Grajcar, M.; Suter, M. Gas ionization chambers with silicon nitride windows for the detection and identification of low energy ions. Nucl. Instrum. Methods Phys. Res. Sect. B 2004, 219–220, 415–419. [Google Scholar]
- Yasuda, K.; Batchuluun, C.; Ishigami, R.; Hibi, S. Development of a TOF-ERDA measurement system for analysis of light elements using a He beam. Nucl. Instrum. Methods Phys. Res. Sect. B 2010, 268, 2023–2027. [Google Scholar] [CrossRef]
- Yasuda, K.; Batchuluun, C.; Ishigami, R.; Hibi, S. Depth resolution of TOF-ERDA using a He beam. Nucl. Instrum. Methods Phys. Res. Sect. B 2011, 269, 1019–1022. [Google Scholar] [CrossRef]
- Yasuda, K.; Tsuchida, H.; Majima, T. Cross-section measurements of α+ 14N elastic scattering for He beam TOF-ERDA. Nucl. Instrum. Methods Phys. Res. Sect. B 2015, 343, 1–5. [Google Scholar] [CrossRef]
- Yasuda, K.; Kajitori, Y.; Oishi, M.; Nakamura, H.; Haruyama, Y.; Saito, M.; Suzuki, K.; Ishigami, R.; Hibi, S. Upgrades of a time-of-flight elastic recoil detection analysis measurement system for thin film analysis. Nucl. Instrum. Methods Phys. Res. Sect. B 2019, 442, 53–58. [Google Scholar] [CrossRef]
- Saito, M.; Fujita, M.; Aoki, Y.; Yoshikawa, M.; Yasuda, K.; Ishigami, R.; Nakata, Y. Effect of water on solid electrolyte interphase formation in Li-ion batteries. Nucl. Instrum. Methods Phys. Res. Sect. B 2015, 371, 273–277. [Google Scholar] [CrossRef]
- Suzuki, K.; Tsuchiya, B.; Yasuda, K.; Nakata, Y. Light element analysis of ceramics using in-air ERDA and TOF-ERDA. Nucl. Instrum. Methods Phys. Res. Sect. B 2020, 478, 169–173. [Google Scholar] [CrossRef]
- Suzuki, K.; Oshigami, R.; Yasunaga, K.; Yasuda, K. Quantitative Ion Beam Analysis for Light Elements using In-air and High Depth Resolution Systems. Trans. Mater. Res. Soc. Jpn, in press.
- Hatori, S.; Kurita, T.; Hayashi, Y.; Yamada, M.; Yamada, H.; Mori, J.; Hamachi, H.; Kimura, S.; Shimoda, T.; Hiroto, M.; et al. Developments and applications of accelerator system at the Wakasa Wan Energy Research Center. Nucl. Instrum. Methods Phys. Res. Sect. B 2005, 241, 862–869. [Google Scholar] [CrossRef]
- Zhang, Y.; Whitlow, H.J.; Winzell, T.; Bubb, I.F.; Sajavaara, T.; Arstila, K.; Keinonen, J. Detection efficiency of time-of-flight energy elastic recoil detection analysis systems. Nucl. Instrum. Methods Phys. Res. Sect. B 1999, 149, 477–489. [Google Scholar] [CrossRef]
- Leo, E.R. Techniques for Nuclear and Particle Physics Experiments; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Bergmaier, A.; Dollinger, G.; Frey, C.M. A compact ΔE-Eres detector for elastic recoil detection with high sensitivity. Nucl. Instrum. Methods Phys. Res. Sect. B 1998, 136–138, 638–643. [Google Scholar]
- Dollinger, G.; Boulouednine, M.; Bergmaier, A.; Faestermann, T.; Frey, C.M. Limits in elastic recoil detection analysis with heavy ions. Nucl. Instrum. Methods Phys. Res. Sect. B 1996, 118, 291–300. [Google Scholar] [CrossRef]






| Facility | Recoil Angle | Flight Length (mm) | T1 Foil | T2 Foil | Solid Angle (msr) | Energy Detector |
|---|---|---|---|---|---|---|
| Zurich [4] | 26°–46° | 950 | 0.5 μg/cm2 Diamond-like carbon (DLC) | 3.0 μg/cm2 Carbon | 0.26 | Gas ionization chamber (GIC) |
| Zagreb [5] | 37.5° | 520 | 0.5 μg/cm2 DLC + LiF | 0.11 | Silicon semiconductor detector (SSD) | |
| Leuven/IMEC [6] | 38.5° | 570 | 3.0 μg/cm2 Carbon | 10.0 μg/cm2 Carbon | 0.44 | SSD |
| Jyväskylä [7] | 41.3° | 623 | 3 μg/cm2 Carbon + 1 nm Al2O3 | 7 μg/cm2 Carbon | 0.29 | SSD |
| WERC [22] | 40° | 589 | 3 μg/cm2 Carbon | 10 μg/cm2 Carbon | 0.09 | SSD |
| Beam | Sample | Count Rate (cps) | Beam Current (Particle nA) | ||
|---|---|---|---|---|---|
| T1 | T2 | SSD | |||
| 12 MeV 63Cu | implant | 1.5 × 104~2.5 × 104 | 1.7 × 102~2.6 × 102 | 60~90 | 0.09~0.15 |
| pure | 1.0 × 104~1.8 × 104 | 1.4 × 102~2.3 × 102 | 50~70 | 0.09~0.14 | |
| 8 MeV 12C | implant | 3.0 × 104 | 7.7 × 102 | 2.9 × 102 | 3.3 |
| pure | 3.2 × 104 | 8.6 × 102 | 3.7 × 102 | 3.3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasuda, K. Time-Of-Flight ERDA for Depth Profiling of Light Elements. Quantum Beam Sci. 2020, 4, 40. https://doi.org/10.3390/qubs4040040
Yasuda K. Time-Of-Flight ERDA for Depth Profiling of Light Elements. Quantum Beam Science. 2020; 4(4):40. https://doi.org/10.3390/qubs4040040
Chicago/Turabian StyleYasuda, Keisuke. 2020. "Time-Of-Flight ERDA for Depth Profiling of Light Elements" Quantum Beam Science 4, no. 4: 40. https://doi.org/10.3390/qubs4040040
APA StyleYasuda, K. (2020). Time-Of-Flight ERDA for Depth Profiling of Light Elements. Quantum Beam Science, 4(4), 40. https://doi.org/10.3390/qubs4040040





