Fast Neutron Scintillator Screens for Neutron Imaging Using a Layered Polymer-Phosphor Architecture
Abstract
:1. Introduction
1.1. Background
1.2. Theory
2. Materials and Methods
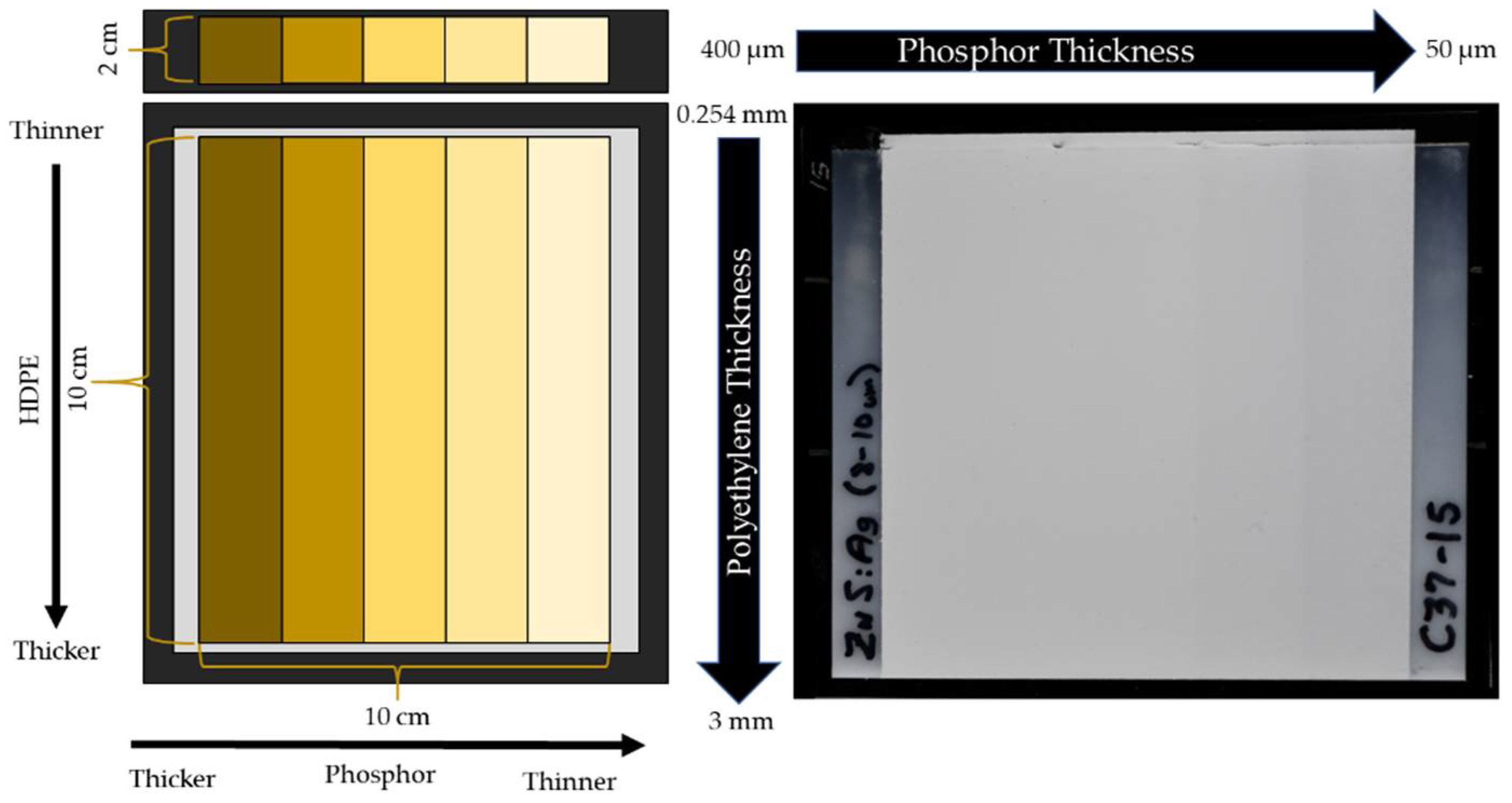
2.1. Layered Scintillator Screens
2.2. Neutron Sources
2.2.1. Idaho National Laboratory’s Neutron Radiography Reactor
2.2.2. Technical University of Munich’s Heinz Maier-Leibnitz Zentrum Reactor
3. Results
3.1. SRIM Simulation Results
3.2. Experimental Results
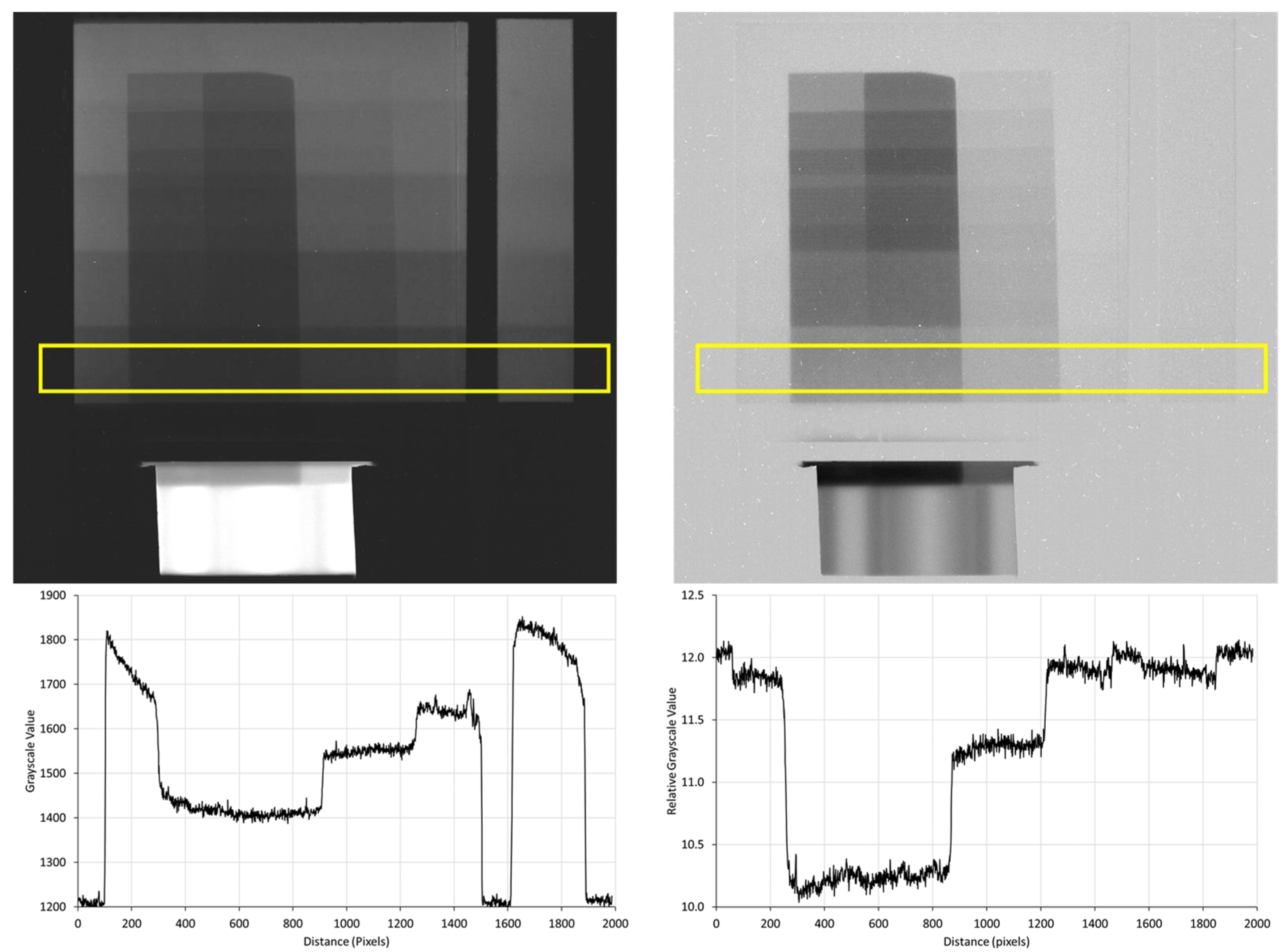
3.2.1. Determination of the Fast Neutron Signal
3.2.2. Imaging with Layered Fast Neutron Screens
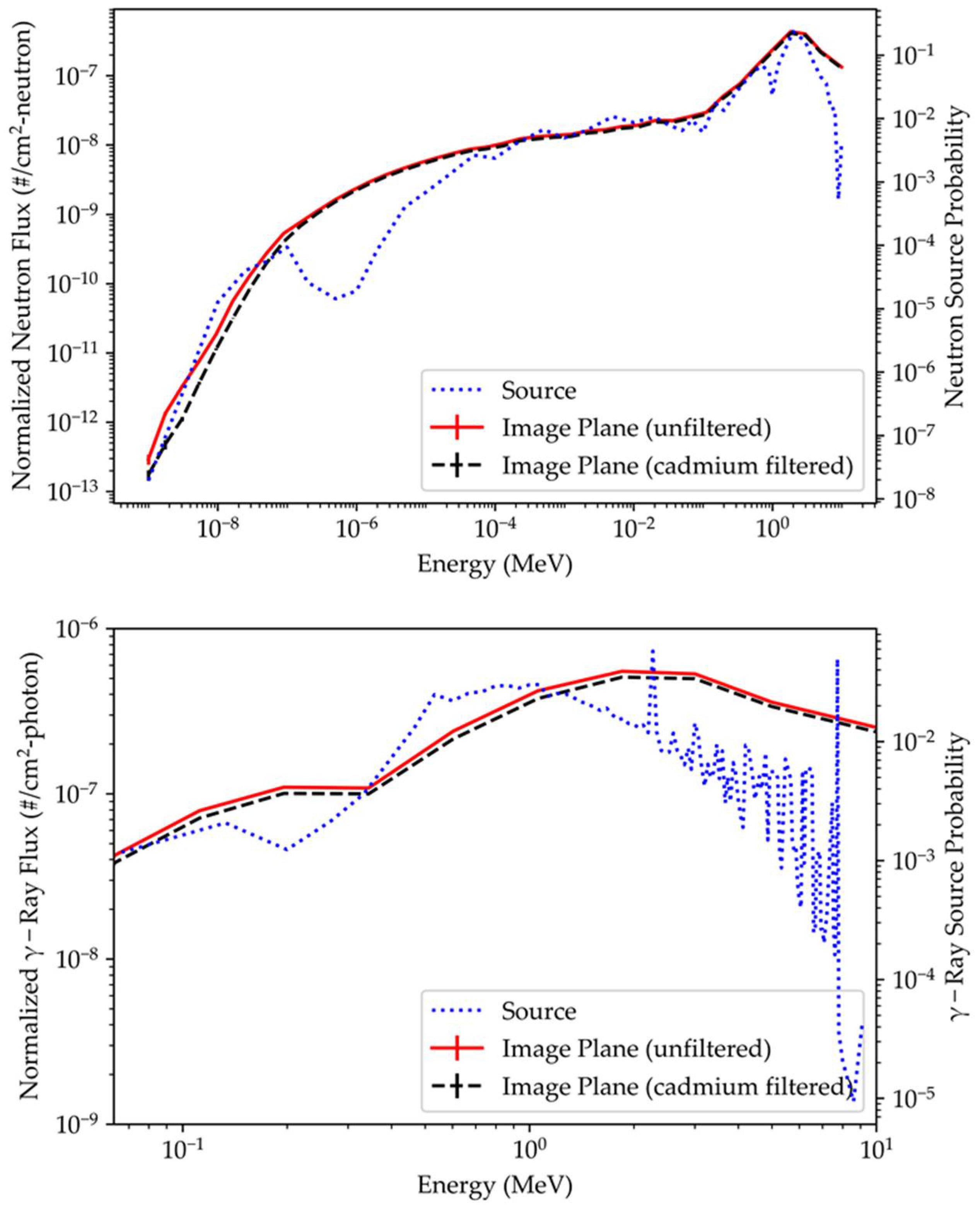
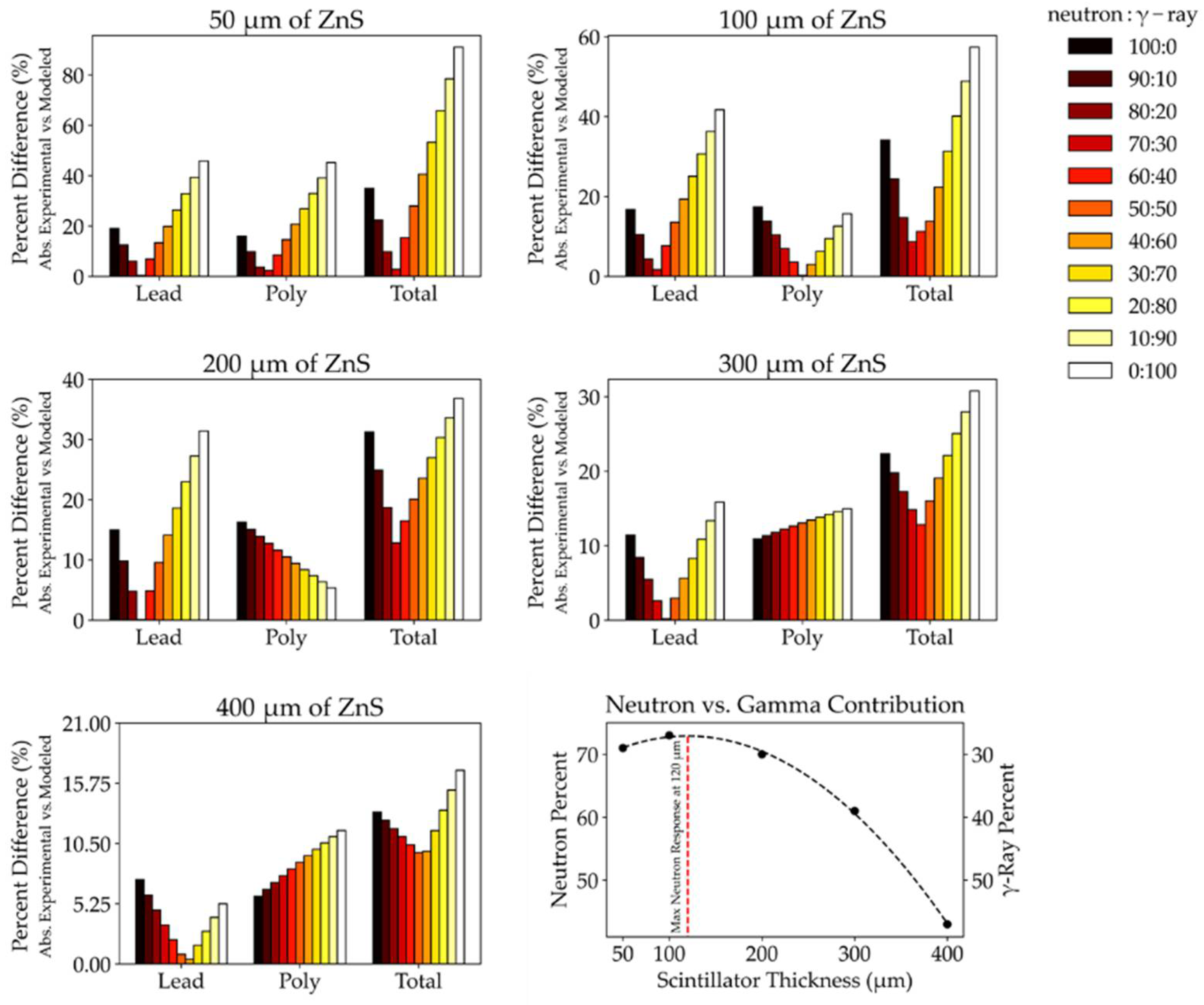
3.3. MCNP Simulation Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Österlund, M.; Blomgren, J.; Donnard, J.; Flodin, A.; Gustafsson, J.; Hayashi, M.; Mermod, P.; Nilsson, L.; Pomp, S.; Wallin, L.; et al. Tomography of canisters for spent nuclear fuel. Proc. Sci. 2006, 25, 030. [Google Scholar] [CrossRef] [Green Version]
- Craft, A.E.; Wachs, D.M.; Okuniewski, M.A.; Chichester, D.L.; Williams, W.J.; Papaioannou, G.C.; Smolinski, A.T. Neutron Radiography of Irradiated Nuclear Fuel at Idaho National Laboratory. Phys. Procedia 2015, 69, 483–490. [Google Scholar] [CrossRef] [Green Version]
- Craft, A.E.; Barton, J.P. Applications of Neutron Radiography for the Nuclear Power Industry. Phys. Procedia 2017, 88, 73–80. [Google Scholar] [CrossRef]
- Eberhardt, J.E.; Rainey, S.; Stevens, R.J.; Sowerby, B.D.; Tickner, J.R. Fast neutron radiography scanner for the detection of contraband in air cargo containers. Appl. Radiat. Isot. 2005, 63, 179–188. [Google Scholar] [CrossRef]
- Buffler, A.; Tickner, J. Detecting contraband using neutrons: Challenges and future directions. Radiat. Meas. 2010, 45, 1186–1192. [Google Scholar] [CrossRef]
- Dangendorf, V.; Kersten, C.; Laczko, G.; Vartsky, D.; Mor, I.; Goldberg, M.B.; Feldman, G.; Breskin, A.; Chechik, R.; Jagutzkyd, O.; et al. Detectors for energy-resolved fast-neutron imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 535, 93–97. [Google Scholar] [CrossRef]
- MacGillivray, G.M. Imaging with neutrons: The other penetrating radiation. Penetrating Radiat. Syst. Appl. II 2000, 4142, 48. [Google Scholar]
- Fujine, S.; Yoneda, K.; Yoshii, K.; Kamata, M.; Tamaki, M.; Ohkubo, K.; Ikeda, Y.; Kobayashi, H. Development of imaging techniques for fast neutron radiography in Japan. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 424, 190–199. [Google Scholar] [CrossRef]
- Bravar, U.; Bruillard, P.J.; Flückiger, E.O.; Macri, J.R.; McConnell, M.L.; Moser, M.R.; Ryan, J.M.; Woolf, R.S. Design and testing of a position-sensitive plastic scintillator detector for fast neutron imaging. IEEE Trans. Nucl. Sci. 2006, 53, 3894–3903. [Google Scholar] [CrossRef]
- Seki, Y.; Taketani, A.; Hashiguchi, T.; Wang, S.; Mizuta, M.; Wakabayashi, Y.; Otake, Y.; Yamagata, Y.; Baba, H.; Kino, K.; et al. Fast neutron transmission imaging of the interior of large-scale concrete structures using a newly developed pixel-type detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2017, 870, 148–155. [Google Scholar] [CrossRef]
- Bertrand, G.H.V.; Hamel, M.; Normand, S.; Sguerra, F. Pulse shape discrimination between (fast or thermal) neutrons and gamma rays with plastic scintillators: State of the art. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2015, 776, 114–128. [Google Scholar] [CrossRef]
- Brooks, F.D. A scintillation counter with neutron and gamma-ray discriminators. Nucl. Instrum. Methods 1959, 4, 151–163. [Google Scholar] [CrossRef]
- Normand, S.; Mouanda, B.; Haan, S.; Louvel, M. Discrimination methods between neutron and gamma rays for boron loaded plastic scintillators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 484, 342–350. [Google Scholar] [CrossRef]
- Feng, P.L.; Villone, J.; Hattar, K.; Mrowka, S.; Wong, B.M.; Allendorf, M.D.; Patrick Doty, F. Spectral-and pulse-shape discrimination in triplet-harvesting plastic scintillators. IEEE Trans. Nucl. Sci. 2012, 59, 3312–3319. [Google Scholar] [CrossRef]
- Lim, A.; Mahl, A.; Latta, J.; Yemam, H.A.; Greife, U.; Sellinger, A. Plastic scintillators with efficient light output and pulse shape discrimination produced via photoinitiated polymerization. J. Appl. Polym. Sci. 2019, 136, 47381. [Google Scholar] [CrossRef]
- Rahmanian, H.; Ambrosi, R.M.; Watterson, J.I.W. Optimisation of resolution in accelerator-based fast neutron radiography. Nucl. Instrum. Methods Phys. Res. A 2002, 477, 378–382. [Google Scholar] [CrossRef]
- Rahmanian, H.; Watterson, J.I.W. Optimisation of light output from zinc sulphide scintillators for fast neutron radiography. Nucl. Instrum. Methods Phys. Res. A 1998, 139, 466–470. [Google Scholar] [CrossRef]
- Zou, Y.; Guo, Z.; Tang, G.; Guo, J.; Bu, T. Comparison of the performance of different converters for neutron radiography and tomography using fission neutrons. Nucl. Instrum. Methods Phys. Res. A 2009, 605, 69–72. [Google Scholar]
- Chuirazzi, W.C. Combinatorial Optimization of Scintillator Screens for Digital Neutron Imaging; The Ohio State University: Columbus, OH, USA, 2020. [Google Scholar]
- Lehmann, E.H.; Mannes, D.; Strobl, M.; Walfort, B.; Losko, A.; Schillinger, B.; Schulz, M.; Vogel, S.C.; Schaper, D.C.; Gautier, D.C.; et al. Improvement in the spatial resolution for imaging with fast neutrons. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2021, 988, 164809. [Google Scholar] [CrossRef]
- Zboray, R.; Adams, R.; Morgano, M.; Kis, Z. Qualification and development of fast neutron imaging scintillator screens. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 930, 142–150. [Google Scholar] [CrossRef]
- Chuirazzi, W.; Craft, A. Measuring Thickness-Dependent Relative Light Yield and Detection Efficiency of Scintillator Screens. J. Imaging 2020, 6, 56. [Google Scholar] [CrossRef] [PubMed]
- Mühlbauer, M.J.; Bücherl, T.; Kellermeier, M.; Knapp, M.; Makowska, M.; Schulz, M.; Zimnik, S.; Ehrenberg, H. Neutron imaging with fission and thermal neutrons at NECTAR at MLZ. Phys. B Condens. Matter 2018, 551, 359–363. [Google Scholar] [CrossRef]
- Schulz, M.; Schillinger, B. ANTARES: Cold neutron radiography and tomography facility. J. Large-Scale Res. Facil. 2015, 1, 8–11. [Google Scholar] [CrossRef] [Green Version]
- Bücherl, T.; Von Gostomski, C.L. Radiography using fission neutrons. Proc. Sci. 2006. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM-The stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2010, 268, 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Losko, A.S.; Han, Y.; Schillinger, B.; Tartaglione, A.; Morgano, M.; Strobl, M.; Long, J.; Tremsin, A.S.; Schulz, M. New perspectives for neutron imaging through advanced event-mode data acquisition. Sci. Rep. 2021, 11, 21360. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuirazzi, W.; Craft, A.; Schillinger, B.; Mendoza, J.; Cool, S.; Losko, A. Fast Neutron Scintillator Screens for Neutron Imaging Using a Layered Polymer-Phosphor Architecture. Quantum Beam Sci. 2022, 6, 14. https://doi.org/10.3390/qubs6020014
Chuirazzi W, Craft A, Schillinger B, Mendoza J, Cool S, Losko A. Fast Neutron Scintillator Screens for Neutron Imaging Using a Layered Polymer-Phosphor Architecture. Quantum Beam Science. 2022; 6(2):14. https://doi.org/10.3390/qubs6020014
Chicago/Turabian StyleChuirazzi, William, Aaron Craft, Burkhard Schillinger, Jesus Mendoza, Steven Cool, and Adrian Losko. 2022. "Fast Neutron Scintillator Screens for Neutron Imaging Using a Layered Polymer-Phosphor Architecture" Quantum Beam Science 6, no. 2: 14. https://doi.org/10.3390/qubs6020014
APA StyleChuirazzi, W., Craft, A., Schillinger, B., Mendoza, J., Cool, S., & Losko, A. (2022). Fast Neutron Scintillator Screens for Neutron Imaging Using a Layered Polymer-Phosphor Architecture. Quantum Beam Science, 6(2), 14. https://doi.org/10.3390/qubs6020014







