Further Optimized Design of a Nested Rotate Sextupole Permanent Magnet Lens for the Focusing of Pulsed Neutrons

Abstract

A compact nested rotate sextupole permanent magnet (Nest-Rot-SPM) lens was designed for the focusing of pulsed neutrons. It is based on the working conditions of the Very Small Angle Neutron Scattering (VSANS) instrument at the China Spallation Neutron Source (CSNS), and is expected to focus a neutron pulse from 6 Å to 10.5 Å, without chromatic aberration. Three hurdles must be addressed, i.e., the tremendous torque, the heat deposition, and the synchronization with the neutron pulse, respectively. The bore diameter and segment length of the lens are optimized using a formula analysis of the key parameters and model simulations of the torque and heat deposition. A twin torque canceling design is used to reduce the torque to one-third of its original value, or even lower. The goal of this project is to take the device into practical use in the VSANS at the CSNS.

1. Introduction

The technique of neutron focusing is essential for the development of SANS instruments. Traditional SANS instruments use the pinhole geometry to collimate the incident neutron beam [1]; thus, they can only measure structures smaller than 100 nm. With the development of neutron optical devices, such as MgF₂ lenses [2], multi-pinhole [3] or multi-slit collimation tools [4], magnetic focusing devices [5], and reflection optics [6], the capacity of the instruments has increased, allowing them to access the minimum scattering vector one order of magnitude smaller than that of the traditional devices, or to increase the neutron flux dramatically. The MgF₂ refractive lenses have been widely utilized in SANS instruments at reactor sources, such as NG7 and NGB [7] at the NIST Center for Neutron Research (NCNR), SANS-J-II [8] at the Japan Atomic Energy Agency (JAEA), 30 m SANS [9] at the China Advanced Research Reactor (CARR), and Suanni [10] at the Mian Yang Research Reactor (MYRR). If polarized neutrons are available, the sextupole magnets bear advantages over the MgF₂ lens, with no material in the neutron path. Researchers have made numerous attempts at creating devices using the sextupole magnets, such as superconducting magnets [11] and coil sextupole magnets [12], but these are still not practical because of the size and cost of superconducting magnets, and the low magnetic field and cooling problems of the coil sextupole magnets. Comparatively, permanent sextupole magnet devices are better [8,13], due to their compactness, low cost, and freedom from maintenance. A permanent sextupole magnet has been successfully installed in SANS-J-II [8].

With the advancement of spallation neutron sources in recent decades, the time-of-flight (TOF) SANS instruments have become increasingly important in the SANS community [14,15,16,17,18]. TOF-SANS uses the time-of-flight of the white neutron pulses from the source to the detector to encode their wavelengths. The consequent chromatic aberration caused by the focal distance being inversely proportional to the square of the neutron wavelength renders the use of MgF₂ lenses and simple permanent sextupole magnets problematic or impossible [19,20,21,22]. By synchronizing the focusing power of the device with the neutron pulse, pioneering efforts have been made to focus these pulsed neutrons. Suzuki et al., for example, employed a pulsed power coil sextupole magnet [12], while Oku and colleagues devised a system with three segments of a sextupole permanent magnet, plus three spin flippers [23], and Iwashita and Yamada et al. created the nested rotating sextupole permanent magnet (Nest-Rot-SPM) [19,20]. Every technique has advantages and disadvantages. The pulsed power coil can operate the magnetic field using an electrical current, but it requires a big power supply, and the magnetic gradient is still not satisfactory; a combination of permanent magnets and spin flippers can only focus a narrow neutron band. Although the Nest-Rot-SPM is one of the most promising techniques under present technological conditions, it still faces significant technical obstacles. All of these difficulties will be discussed below.

Figure 1 depicts the working mechanism of a typical Nest-Rot-SPM. The outer ring of the Nest-Rot-SPM spins relative to the inner ring, causing the strength of the central magnetic field to alter regularly. The rotation should be synchronized with the neutron pulse to maintain the focal distance, thereby eliminating the chromatic aberration. Iwashita and Yamada et al. developed and test a Nest-Rot-SPM prototype using ultra-cold neutrons ranging from about 26 Å to 60 Å [19,20]. However, the flux of such an ultra-cold neutron in a spallation neutron source is extremely low. In a real TOF-SANS experiment, only neutrons with a wavelength shorter than 15 Å, preferably less than 10 Å, are usable.

Three problems must be overcome in order to focus neutrons with wavelength less than 10 Å with the Nest-Rot-SPM. First, the strong alternative torque may destroy the permanent magnets of the inner sextupole, necessitating the use of a very powerful motor to drive the outer sextupole; second, the heat from the eddy current and hysteresis loss in the inner circle may raise the temperature and disable the permanent magnets; and third, the motors must be synchronized with the repetition of the neutron source. If we regulate the speed in one cycle so that the magnetic field decays with the square of inverse time (t⁻²), we can keep the focal distance of the chromatic neutrons passing through the lens successively.

The following paragraph will conduct theoretical analysis and physical simulations to assess the feasibility and challenges of implementing the Nest-Rot-SPM in VSANS at the CSNS. It is a typical TOF multi-slit VSANS instrument with polarizing capability, and it will be commissioned by the end of 2022.

2. Principle of the Nest-Rot-SPM

The intrinsic magnetic moment of each neutron is −1.91 nuclear magnetic moment in magnitude. Spin-up and spin-down are the two quantum states [25]. When a neutron’s spin vector is oriented parallel to the magnetic field, it is in the spin-up state; when it is oriented anti-parallel to the magnetic field, it is in the spin-down state; and when its spin vector maintains an angle and processes relative to the magnetic field, it is in a mixture state of spin-up and spin-down. Because the mixed state is usually undesirable, we polarize the neutron by absorbing or reflecting half of the neutrons with one spin state and maintaining the other spin state. As shown in Figure 2, when a group of polarized cold neutrons with polarizing vectors parallel to the x-axis enters the magnetic lens from the negative direction of the z-axis to the positive direction, the direction of their spin changes adiabatically, following the magnetic field direction of the lens. The magnitude of the magnetic field in the sextupole magnetic lens grows proportionally to the square of the radius of the sextupole meanetic lens. The magnetic field will exerted a force on the spin of the neutron in a direction parallel (spin-up) or antiparallel (spin-down) to the magnetic gradient’s direction. As a result, the radial gradient magnetic field of the sextupole is able to converge the polarized neutrons.

To get a better understanding of the magnetic focusing, we transfer the Cartesian coordinates to polar coordinates and describe the migration of neutrons using the following formulas:

$$\frac{d^2\stackrel{\rightharpoonup }{r}}{{\mathit{dt}}^2}=-\alpha \stackrel{\rightharpoonup }{\nabla }({\stackrel{\rightharpoonup }{\sigma }}_n\cdot \stackrel{\rightharpoonup }{B})$$

(1)

$$\frac{d\stackrel{\rightharpoonup }{\sigma }}{\mathit{dt}}{=\gamma }_n({\stackrel{\rightharpoonup }{\sigma }}_n\times \stackrel{\rightharpoonup }{B})$$

(2)

where, ${\stackrel{\rightharpoonup }{\sigma }}_n$ is the neutron spin vector, $\stackrel{\rightharpoonup }{B}$ is the magnetic field vector, $\alpha =\left|\frac{{\mu }_n}{m_n}\right|$ = 5.77 m²s⁻²T⁻¹, ${\mu }_n$ is the neutron magnetic moment, $m_n$ is the neutron mass, ${\gamma }_n$ = 1.83E8, rads⁻¹T⁻¹ and it is the neutron gyromagnetic ratio. When the angle between the spin direction of the neutron and the direction of the magnetic field $\theta$ is not zero, the neutron processes in the magnetic field, and the precession frequency is the Larmor frequency ${\omega }_L$:

$${\omega }_L{=\gamma }_n|\stackrel{\rightharpoonup }{B}|$$

(3)

Usually, the magnetic field of a sextupole magnet is very strong, as for the cold neutrons, and the neutron spin can rotate adiabatically following the direction of the magnetic field. When $\theta$ is zero,

$${\stackrel{\rightharpoonup }{\sigma }}_n\cdot \stackrel{\rightharpoonup }{B}=|\stackrel{\rightharpoonup }{B}|\times \mathit{cos}\left(\theta \right)=|\stackrel{\rightharpoonup }{B}|$$

(4)

Under the adiabatic approximation, Equation (1) can be rewritten as

$$\frac{d^2\stackrel{\rightharpoonup }{r}}{{\mathit{dt}}^2}=-\alpha \stackrel{\rightharpoonup }{\nabla }|\stackrel{\rightharpoonup }{B}|$$

(5)

For a sextupole magnet, the distribution of the internal magnetic field is

$$B=G\left(\begin{array}{l}{(y}^2-x^2)/2\\ \mathit{xy}\\ 0\end{array}\right)$$

(6)

where, $G$ is the magnetic field gradient, and it is called G factor. Its unit is T/m². The radial magnetic field distribution can be obtained with the square root of the sum of the square of the magnetic field in the x and y direction.

$$|\stackrel{\rightharpoonup }{B}|=\frac{G}{2}\times \frac{x^2{+y}^2}{2}$$

(7)

Substituting Equation (7) into Equation (5), we get

$$\{\begin{array}{l}\frac{d^{2}x}{{\mathit{dt}}^2}=-{\omega }^{2}x\\ \frac{d^{2}y}{{\mathit{dt}}^2}=-{\omega }^{2}y\\ \frac{d^{2}z}{{\mathit{dt}}^2}=0\end{array}$$

(8)

Solve Equation (8) and substitute it into the boundary conditions,

$$\{\begin{array}{l}{r\left(0\right)=r}_0\\ \frac{\mathit{dr}}{\mathit{dt}}{\left(0\right)=v}_0\end{array}$$

(9)

We get

$$\{\begin{array}{l}{x=x}_0\mathit{cos}\left(\omega t\right)+\frac{v_{x0}}{\omega }\mathit{sin}\left(\omega t\right)\\ {y=y}_0\mathit{cos}\left(\omega t\right)+\frac{v_{y0}}{\omega }\mathit{sin}\left(\omega t\right)\\ {z=v}_{z}t\end{array}$$

(10)

As shown in Figure 2, a beam of parallel neutrons enters the magnetic focusing lens from the origin in the z direction, and is focused to point C. Initial velocity of the neutrons in the x, y direction is denoted as ($v_{x0}$, $v_{y0}$). Angular frequency of a neutron traveling in the magnetic field is $\omega =\sqrt{G\alpha }$. The neutron velocity in the z-direction $v_z$ has a large value that can be approximated as a constant. The velocity of neutrons in the x and y directions can be written as

$$\{\begin{array}{l}{v}_x{=v}_{x0}\mathit{cos}\left(\omega t\right)-{\omega x}_0\mathit{sin}\left(\omega t\right)\\ v_y{=v}_{y0}\mathit{cos}\left(\omega t\right)-{\omega y}_0\mathit{sin}\left(\omega t\right)\end{array}$$

(11)

Assuming that a neutron goes from point A to point B after time t with $v_{x0}=0$ and $y_0=0$, using Equations (10) and (11), we get

$$\{\begin{array}{l}{x}_1{=x}_0\mathit{cos}\left(\omega t\right)\\ v_{x1}=-{\omega x}_0\mathit{sin}\left(\omega t\right)\\ z_m{=v}_{z}t\end{array}$$

(12)

According to the geometry in Figure 2, $\mathit{tan}\left(\theta \right)=\frac{\mathit{BD}}{\mathit{CD}}=\frac{\left|v_{x1}\right|}{\left|v_z\right|}$, we get

$$z_f{=z}_m+\frac{\left|x_1\right|}{\mathit{tan}\left(\theta \right)}{=z}_m+\left|x_1\right|\frac{\left|v_z\right|}{\left|v_{x1}\right|}$$

(13)

Substituting (12) into (13), we get

$$z_f{=z}_m+\frac{\left|v_z\right|}{\omega }\mathit{ctg}(\frac{{\omega z}_m}{\left|v_z\right|})$$

(14)

Image that another magnetic lens is put on the left side of the original one, as shown in Figure 2, and a diverse neutron beam emitted from the point $-z_m$ is focused by the two lenses to point C. According to the concept of lens imaging, light from the point two times the focal distance of the lens will be focused to another point, also two times the focal distance of the lens. Thus, the combined lens with a length of ${2z}_m$ has a focal length of $\frac{z_f}{2}$. Therefore, a lens with length ${z^{\prime }}_m{=2z}_m$ has a focal distance

$$f_m=\frac{{z^{\prime }}_m}{4}+\frac{h}{{2m}_n\omega \lambda }\mathit{ctg}(\frac{m_n\omega \lambda }{2h}{z^{\prime }}_m)$$

(15)

where $\left|v_z\right|=\frac{h}{m_n\lambda }$, $h=6.63\times {10}^{-34}J\cdot s$ is the Planck constant, and ${z^{\prime }}_m$ is the length of the lens. If $c=\frac{h}{m_n}$ and $\omega =\sqrt{G\alpha }$, (15) can be rewritten as

$$f_m=\frac{{z^{\prime }}_m}{4}+\frac{c}{2\lambda \sqrt{G\alpha }}\mathit{ctg}(\frac{\lambda \sqrt{G\alpha }}{2c}{z^{\prime }}_m)$$

(16)

where $c=3.9562$ mÅ/ms, $G$ is the magnetic gradient factor; its unit is T/m².

Assuming that the distance from the moderator to the lens is L, the flight time of a neutron with a wavelength of λ is

$$t\left(\mathit{ms}\right)=\frac{L\left(m\right)\lambda (\AA )}{3.9562}$$

(17)

According to Formulas (16) and (17), if f_m is required to be constant, the G factor should be reversely proportional to the square of the wavelength, or that of the flight time t, $G=\frac{1}{2}{\mathit{Br}}^2\propto \frac{1}{{\lambda }^2}\propto \frac{1}{t^2}$. Assuming a periodical change of the strength of the G factor from T_b to T_e and at an intermediate time T_p, the G factor reaches a maximum $G_p$ and the ideal G factor in a cycle of the neutron pulse is

$$G=\{\begin{array}{l}{G}_{\mathit{min}}\begin{array}{ccc}& & \end{array}{(T}_b<t<T_p)\\ G_p{\left(\frac{T_p}{t}\right)}^2\begin{array}{cc}& \end{array}{(T}_p{\text{ < }t\text{ < }T}_e)\end{array}$$

(18)

Figure 3 depicts the CSNS-VSANS time-distance diagram. The positions and the opening time range of the three disc choppers and neutrons from 6 Å to 10.5 Å transmitting the choppers are presented. The lens and the sample are around 21.5 m apart from the moderator. A pulse’s neutron will pass through the lens from T_p to T_e, but no neutrons will pass through the lens from T_b to T_p. As illustrated in the inset of Figure 3, the G factor should remain constant at $G_{min}$ from T_b to T_p, rise suddenly from $G_{min}$ to $G_p$ at T_p, and then decrease from T_p to T_e, according to Formula (18).

As for an electromagnet, it is quite simple to generate a magnetic field that decays inversely with the square of time. When it comes to the Nest-Rot-SPM, the rotational speed of the motor must be regulated to modulate the magnetic field. When the motor rotates at a constant speed, the magnetic field gradient variation follows a cosine function from $G_{\mathit{min}} \mathrm{to} G_{\mathit{max}}$.

$$G=\frac{1}{2}{(G}_{\mathit{max}}{+G}_{\mathit{min}})+\frac{1}{2}{(G}_{\mathit{max}}-G_{\mathit{min}}\left)\mathit{cos}\right(3\theta -\phi )$$

(19)

where, θ is the rotating angle and $\phi$ is the phase angle. When Formulas (18) and (19) are combined, we get the relationship between the rotating angle θ and the time t

$$\theta =\{\begin{array}{l}\frac{1}{3}\left({\omega }_{0}t+\phi \right)(t\text{ < }{T}_p)\\ \frac{1}{3}\mathit{arccos}\left[\frac{{2G}_p}{G_{\mathit{max}}-G_{\mathit{min}}}{\left(\frac{T_p}{t}\right)}^2-\frac{G_{\mathit{max}}{+G}_{\mathit{min}}}{G_{\mathit{max}}-G_{\mathit{min}}}\right]\begin{array}{cc}+\frac{1}{3}\phi & \end{array}(t\ge T_p)\end{array}$$

(20)

where, ${\omega }_0$ is an adjustable value used to synchronize the device with the neutron pulse. We derive the rotating angular frequency by taking the derivative of Formula (20) over t.

$$\omega =\{\begin{array}{l}\frac{1}{3}{\omega }_0\left(t\text{ < }{T}_p\right)\\ -\frac{{4G}_p{T}_p{}^2}{{3(G}_{\mathit{max}}-G_{\mathit{min}}{)t}^3}/\sqrt{1-{\left(\frac{{2G}_p{T}_p{}^2}{{(G}_{\mathit{max}}-G_{\mathit{min}}{)t}^2}-\frac{G_{\mathit{max}}{+G}_{\mathit{min}}}{G_{\mathit{max}}-G_{\mathit{min}}}\right)}^2}(t\ge T_p)\end{array}$$

(21)

Because the angular velocity cannot change abruptly, we suppose that in a cycle T (T = T_e −T_b), the angular velocity of the sextupole magnet initially speeds up from ${\omega }_b$ to ${\omega }_p$ in the time range of T_b to T_p, then decays to ${\omega }_b$ in the time range of T_p to T_e, using the Formula (21). Then the angular velocity can be stated as

$$\omega =\{\begin{array}{l}\frac{{\omega }_p-{\omega }_b}{T_p-T_b}{t+\omega }_e-\frac{{\omega }_p-{\omega }_b}{T_p-T_b}{T}_b(T_b\text{ < }t\text{ < }{T}_p)\\ -\frac{{4G}_p{T}_p{}^2}{{3(G}_{\mathit{max}}-G_{\mathit{min}}{)t}^3}/\sqrt{1-{\left(\frac{{2G}_p{T}_p{}^2}{{(G}_{\mathit{max}}-G_{\mathit{min}}{)t}^2}-\frac{G_{\mathit{max}}{+G}_{\mathit{min}}}{G_{\mathit{max}}-G_{\mathit{min}}}\right)}^2}{(T}_p\le t\le T_e)\end{array}$$

(22)

where, ${\omega }_p$ and ${\omega }_b$ can be calculated from the boundary conditions of (22) by substituting T_b, T_p, and T_e into the formula.

In actuality, to control the angular velocity of the Nest-Rot-SPM, according to Formula (22), a fairly powerful motor is required. The motor will typically rotate at a constant angular speed, with the G factor changing sinusoidally over time. The sine function’s high falling edge may be approximate to the ideal 1/t² dropping.

3. Design of the Nest-Rot-SPM

The focal distance f and the bore diameter, like the optical lens, are the two key parameters. To make sure that the two parameters are developed as close to the practical application as possible, CSNS-VSANS is adopted as a platform for the test and validation of the device. The layout of the CSNS-VSANS is shown in Figure 4. The focusing device can be set up in front of the sample at a distance of 22 m from the moderator. The four-blade-slit at 12 m from the moderator can be used as a variable source aperture; then, L₁ equals 10 m. At 34.75 m from the moderator (L₂ equals 12.75 m), there is a high resolution position sensitive detector (approximately 2 mm resolution and 200×200 mm sensitive area). The source aperture, Nest-Rot-SPM, and the high resolution detector form a complete lens imaging geometry.

If the focal distance of the lens f, object distance L₁ and the image distance L₂ satisfy the imaging formula of lenses (23), an image of the source aperture or object can be projected to the detector.

$$\frac{1}{f}=\frac{1}{L_1}+\frac{1}{L_2}$$

(23)

According to Figure 4, if a 1 m long lens is put directly before the sample at 22 m, then L₁ and L₂ would be 9.5 m and 13.25 m, respectively. As a result, using Formula (23), the focal distance can be calculated to be about 5.5 m. The wavelength band of the VSANS instrument is about 4.5 Å, according to Formula (24), with T_tof = 40 ms (25 Hz repetition rate) and L_tof = 34.75 m. When the wavelength band of 6 Å to 10.5 Å is chosen for the focusing experiments, the lens should maintain a constant focal distance of roughly 5.5 m.

$$\Delta \lambda (\AA )=\frac{3{.9562\mathrm{T}}_{\mathrm{tof}}\left(\mathrm{ms}\right)}{{\mathrm{L}}_{\mathrm{tof}}\left(\mathrm{m}\right)}$$

(24)

Another important consideration is the bore diameter. An appropriate bore diameter is crucial to the design of the device. The G factor is proportional to the square of the bore diameter, whereas the neutron current is inversely proportional. According to Yamada et al., the maximal surface magnetic field at the inner surface of the sextupole magnet, using the Halbach arrangement and paramagnet materials, is roughly 1.7 T [20]. The maximum G factor can then be calculated with a known bore diameter. The G factors for bore diameters of 15 mm, 20 mm, and 27 mm are calculated to be 6 × 10⁴ T/m², 3.4 × 10⁴ T/m², and 1.86 × 10⁴ T/m², respectively. For the selection of these bore sizes, the space at the sample site of the CSNS-VSANS instrument will be evaluated.

In a SANS instrument, neutrons are frequently polarized by a polarizing supermirror with transmission geometry. The obtained spin-down neutrons obtained will be defocused by the lens. Thereby, a polarizing flipper must be inserted before the lens to flip the spin-down neutrons to spin-up. Only roughly 1.6 m of space remains in the CSNS-VSANS for the polarizer, lens, and sample; thus, the lens must be less than 1 m. The focal distance of the lens is a function of the neutron wavelength, G factor, and lens length, according to Formula (16). As shown in Figure 5, the focal distance of the lenses of various lengths and the G factors at various neutron wavelengths are determined. Using a 0.5 m lens with a G factor of around 3 × 10⁴ T/m², 6 Å neutrons may be focused with a focal distance of around 5.5 m. The G factor of 3 × 10⁴ T/m² corresponds to a bore diameter of about 20 mm, according to previous analysis.

Yamada et al., from Kyoto University [26], created the first prototype of the Nest-Rot-SPM. The prototype’s inner circle employs the Halbach scheme, with the paramagnetic alloy Fe₄₉Co₄₉V₂ and the NEOMAX-32H NdFeB permanent magnets. The inner bore is 15 mm in diameter. They used a coaxial Nest-Rot-SPM with a phase difference of 60 degrees to offset about 2/3 of the torque [26]. The differential resistance of Fe₄₉Co₄₉V₂ is 40 µΩ cm (

Table 1. Differential resistance of NdFeB, Fe₄₉Co₄₉V₂, and ordinary wires.

Materials	Micro Resistivity (20 °C) µΩ·cm
NdFeB magnet	140~160 [27]
Copper wire	1.724~1.796
Aluminum wire	2.8~2.8264
Fe49Co49V2	40 [28]

), which is less than a quarter of that of the NdFeB. During the functioning of the device, it is easy to generate eddy current and heat, which will compromise the magnet’s performance. Yamada et al. decreased the working temperature from 29 degrees to 18 degrees [26] by cutting the Fe₄₉Co₄₉V₂ sheet into a 2.5 mm thickness, but they believed that 2.5 mm was insufficient.

Simulations are the only way to determine the value of the static magnetic field, torque, and heat deposition inside the inner sextupole. The simulations are carried out using models created with ANSYS. A permanent magnet, N52 NdFeB, and a soft magnet, 1J22 Fe₄₉Co₄₉V₂, are used in the simulations. To reduce eddy current, the permanent magnets are stacks of laminated 10 mm thick pieces, and the soft magnets are stacks of laminated 0.35 mm thick thin films. Model 1 and model 2, are simulated with bore diameters of 20 mm and 27 mm, respectively, as shown in Figure 6. The inner and the outer sextupoles are separated by a 1 mm gap. The length of model 1 and model 2 are 100 mm and 50 mm, respectively, as shown in Figure 6c,d.

3.1. Simulations of the Static Magnetic Field

Figure 7 and Figure 8 illustrate the static magnetic fields of the two models with rotating angles of 0° and 60°. Two types of magnetic fileds are monitored, i.e., the radial magnetic field B_r and the tangential magnetic field B_t. As shown in Figure 6, B_r and B_t are monitored close to the inner surface along the z-axis and also around the z-axis.

Model 1 and model 2 have a maximum B_r of 1.75 T and 1.6 T, respectively, corresponding to magnetic gradients of 3.5 × 10⁴ T/m² and 1.92 × 10⁴ T/m². Model 1’s magnetic gradient is large enough to converge 6 Å neutrons to the detector of the CSNS-VSANS instrument with a lens less than 1 m. Sharp, narrow, non-natureal peaks can be seen in the B_r and B_t plots, which may originate from the defects of the ANSYS models.

The simulated B_r and B_t of model 1 and model 2, when the rotating angle is 60 degrees, are presented in Figure 8. For both model 1 and model 2, the maximum B_r is around 0.35 T, corresponding to the magnetic gradients of 7 × 10³ T/m² and 3.8 × 10⁴ T/m², respectively. Model 1 has a magnetic gradient range of 7 × 10³ T/m² to 3.5 × 10⁴ T/m², with a rotating angle of 0° to 60°, covering the required range from 8571 T/m² to 3 × 10⁴ T/m², as shown in Figure 5b. The magnetic field at the inner surface can be calculated to be 1.8 T by Formula (7), which is comparable to the simulated results of 1.4 T by Yamada et al. [20], since they use N38 permanent magnets.

3.2. Simulation of the Torque

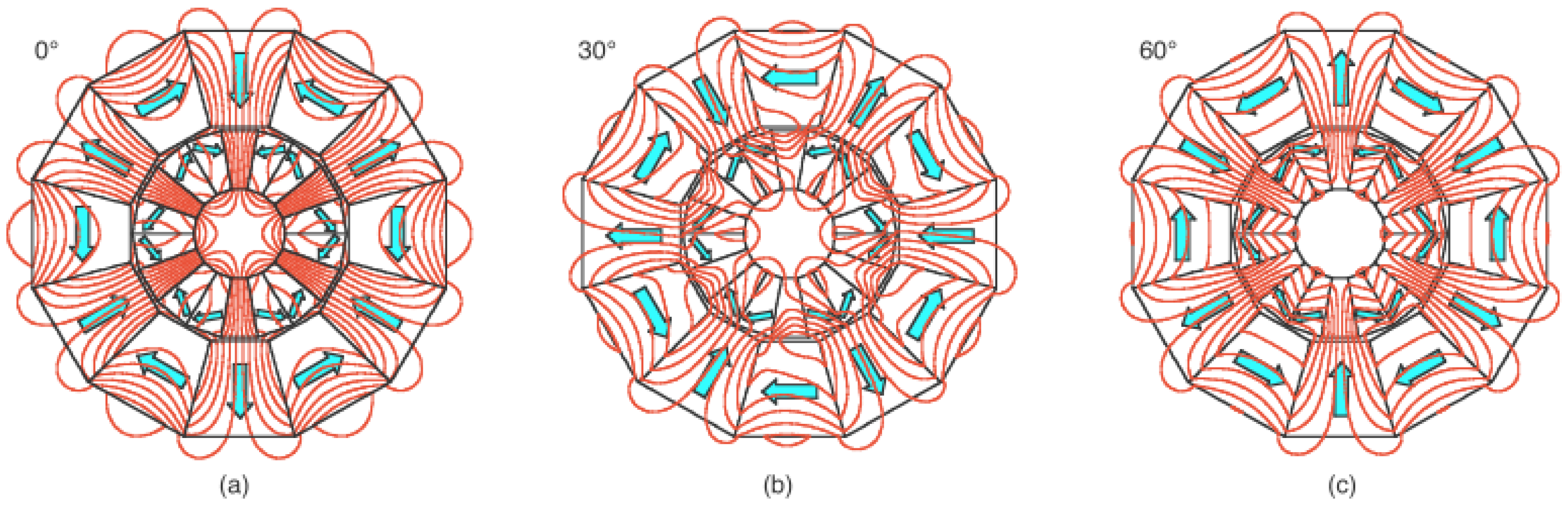
There will be an alternative torque between the inner and outer sextupoles when rotating the latter. This is due to the same-pole attract, opposite-pole repel principle. As shown in Figure 1, the three northern poles of the outer sextupole face the three southern poles of the inner sextupole at 0°, whereas the three southern poles of the outer sextupole face the three northern poles of the inner sextupole. Except for the strongest magnetic field in the bore of the lens, all attractive forces are balanced, and there is no torque. There is a magnetic torque drawing the outer poles back to 0° at 30° due to the attraction between the six poles of the outer sextupole and the six poles of the inner sextupole. At 60°, the three northern pole of the outer sextupole faces the three northern pole of the inner sextupole, while the three southern poles of the outer sextupole face the three southern poles of the inner sextupole. Except for the lowest magnetic field in the bore of the lens, all the repulsive forces are balanced, and there is no torque. At 90°, the outer poles are propelled forward by the repulsive forces to 120° which is the angular cycle of the torque. Since the torque first drew back the rotation from 0° to 60° and then pushed forward the rotation from 60° to 120°, the torque should be mostly countered with two identical Nest-Rot-SPMs with a 60° phase difference linked together by gears or a belts. B rotating the outer circle at a speed of 500 revolutions per minute, the torque between the inner and outer sextupole is simulated. Figure 9 displays the results of the torque simulation results for model 1 and model 2. The maximum torques for Models 1 and 2 are 182 Nm and 164 Nm, respectively. A powerful motor is needed to drive the outer circle with such a large torque. The torque curves resemble an asymertric sine function. According to Figure 9a, the torque first rises from 0 to 182 Nm and then decreases back to 0 Nm from 0 to 20 ms, and then it increases from 0 to −182 Nm (negative signifies the opposite of the direction of rotation) and then descends back to 0 Nm from 20 to 40 ms. By shifting the curve in Figure 9a by 20 ms (or 60°), it will be a mirror image of the original curve and a force offset the original torque. Therefore, the majority of the torque can be countered by a twin Nest-Rot-SPM with a 60° phase shift.

Figure 10 depicts the torque canceling effect with two identical Nest-Rot-SPMs with 60° phase difference. The leftover torque of the twin Nest-Rot-SPMs is around one-third of that of a single Nest-Rot-SPM, which is the same as the results from the reference [20]. Because the repetition rate of the residual torque is two times lower than the original rate, it can be further reduced with a small torque canceler that rotates twice as fast as the Nest-Rot-SPM.

3.3. Simulation of the Heat and Temperature

The outer ring permanent magnet model is not included in the thermal simulation model, since it is a high-speed rotating body with low internal losses and a good heat dissipation effect. Convection heat dissipation at both ends is taken into account in the model. The effect of the insulating material between the permanent magnets on heat simulations is not taken into account. The ambient temperature is 20 °C.

Figure 11 depicts the heat power generated in the inner sextupole by the eddy current and hysteresis loss of model 1 and model 2. Model 1 has a time averaged eddy current loss of around 1.2 W and a hysteresis loss of about 3.6 W, totaling 5.7 W. Model 2 has time averaged eddy current loss of around 1.0 W and a hysteresis loss of about 2.8 W, totaling 3.8 W.

The eddy current loss and the hysteresis loss are used in the temperature distribution simulations. The hottest region is centered in the middle of the sextupole, as seen in Figure 12. The highest temperatures in model 1 and model 2 are 188.1 °C and 158.5 °C, respectively. To lower the temperature of the inner sextupole, high performance NdFeB magnets should be used, and measurements, including water cooling, should be taken.

3.4. Modulation of the Angular Velocity

When the Nest-Rot-SPM rotates at a constant angular velocity, the magnetic gradient will change following Formula (19). However, it may not follow the 1/t² decay based on the magnetic field simulations under the working conditions of the CSNS-VSANS instrument, as illustrated in Figure 13c. Figure 13a shows how the magnetic gradient can be modulated to meet the 1/t² decay curve by modulating the angular velocity of the outer sextupole based on Formula (22). The resulting G factor over time compared with the 1/t² decay is demonstrated in Figure 13d. It shows that, by modulating the angular velocity, the chromatic aberration can be effectively eliminated.

4. Other Considerations

Simulations show that both the torque and the heat deposition will push the limits of the materials. The inner circle of the sextupole needs to be strengthened and cooled. First, a copper rod with a diameter of about 4 mm can be used to string the stacks of Fe₄₉Co₄₉V₂ films together, as shown in Figure 6. Beryllium copper rods can provide sufficient strength, while also allowing heat to be exported from the core. Second, water cooling at both sides of the inner circle can aid in the quick removal of heat. Third, to prevent the occurrence of cracks, portions of the permanent magnets and stacks of soft magnets can be firmly bound with high performance fiber, such as carbon fiber or Kevlar.

According to the simulations above, the section length of model 1 and model 2 should be no more than 100 mm and 50 mm, respectively, because otherwise, the torque and the heat deposition will exceed the limit of the inner circle of the sextupole. With the parameters of model 1, seven sections of 100 mm length Nest-Rot-SPM may be able to focus 6 Å to 10.5 Å neutrons in CSNS-VSANS. With gears driving, the entire system can be quite compact. Torque cancelers can also be linked to the gears. Other difficulties include precise machining and gluing of the soft magnets, synchronizing the system with the neutron pulse, and modulating the angular velocity. As a result, a segment prototype of the entire system will be built initially. This prototype can be put to the test to meet all of these challenges and prepare the way for the construction of the entire system, which is then nothing more than the simple assembly of distinct components.

5. Conclusions and Prospect

A practical Nest-Rot-SPM Lens has been designed based on the experimental setup of the CSNS-VSANS. The focal distance of the lens has been determined to be 5.5 m by formula analysis. Key parameters, such as bore diameter, maximum torque, and heat deposition have been obtained by simulations. A torque cancelling design has been presented, as well as measurements of reinforce the inner circle of the sextupole magnet. In theory, this study has opened up the prospect of focusing the white neutrons in a TOF-SANS instrument. However, building a workable Nest-Rot-SPM lens still poses material and technical obstacles. More research is needed to tackle these technical issues to improve the capacity of modern TOF-SANS instruments and energy-resolved neutron imaging instruments.