1. Introduction
In this paper, we point out for the first time a remarkable analogy between the pattern structure of bonds between amino acids in a protein (the protein secondary structure [
1]) and the non local structures observed in tonal music and in poems. We explain the origin of these analogies with finitely generated groups and graph covering theory.
A protein is a long polymeric linear chain encoded with 20 letters (the 20 amino acids). The surjective mapping of the
codons to the 20 amino acids is the DNA genetic code. It can be given a mathematical theory with appropriate finite groups [
2,
3]. In addition, a protein folds in the three dimensional space with structural elements such as coils,
-helices and
-sheets, or other arrangements that determine its biological function. The number of proteins encoded in genomes depends on the biological organism (typically from 1 to
proteins in viruses, from
to
proteins in bacteria and from
to
proteins in eukaryotes). The protein database (or PDB) contains about
entries [
4]. Proteins ensure the language of life, amino acids are the alphabet, proteins are the words and the set of proteins in an organism are the phrases.
Analogously in music, a note is a letter encoding a musical sound. In the 12-tone chromatic scale [
5], each of the 12 notes (or letters) has the frequency of the previous note multiplied by
. The form refers to the secondary structure of a musical composition in terms of clear-cut units of equal length, for example, A-B-A in the sonata form or A-B-C-B-A in an arch form [
6].
Now, we come to human language and the Latin alphabet. There are 26 letters organized into words of various types such as names, adjectives, verbs, and so on. In the following, we will show that a verse in a poem or a phrase in prose have distinctive features, the former being closer to our theory.
Our mathematical theory of the secondary structures in proteins, music and poems relies on the concept of a finitely generated group and the corresponding graph coverings, as explained in
Section 2.
We will investigate three applications of the graph covering approach. In
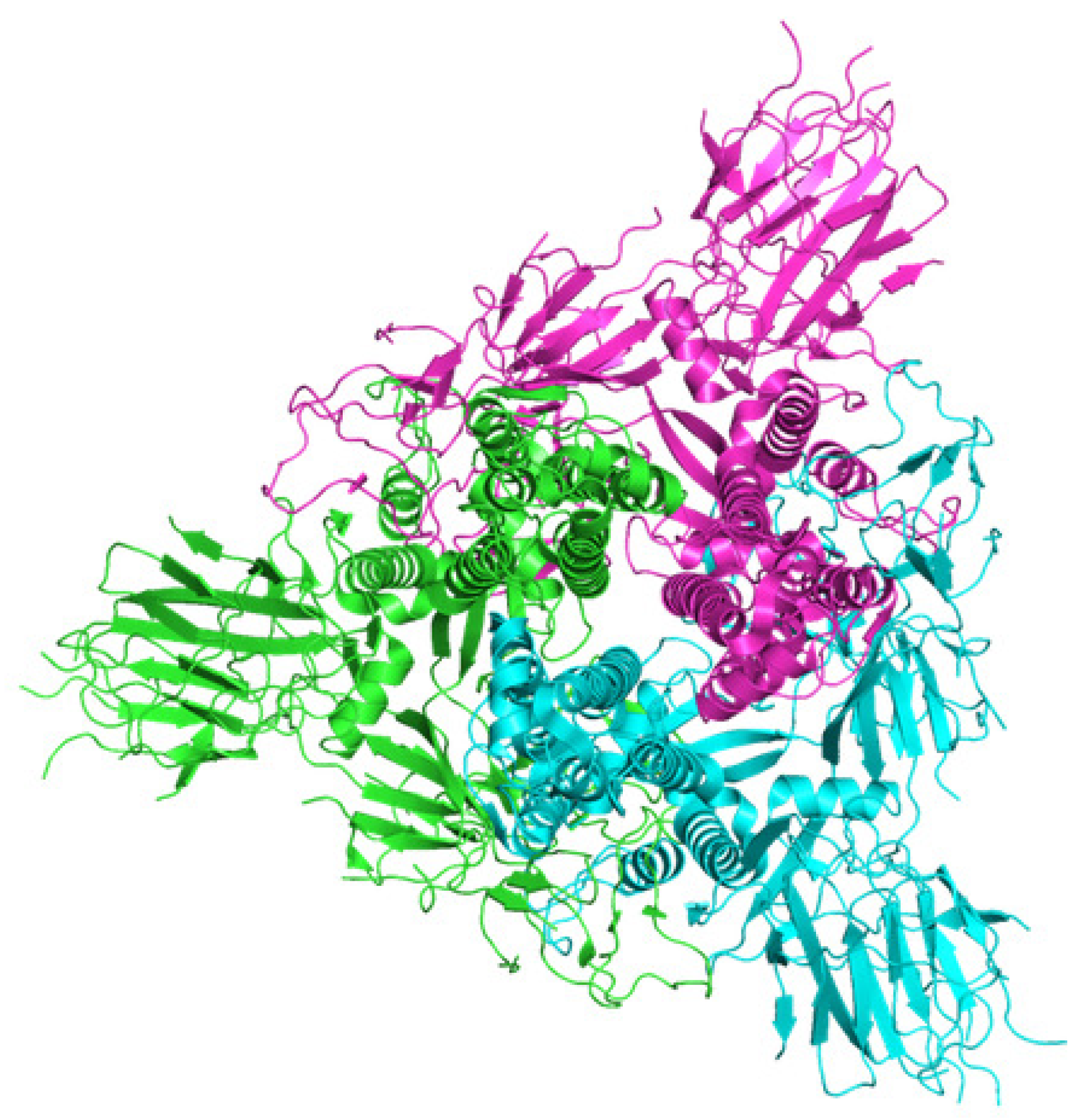
Section 3, we look at the secondary structures of two proteins. We take as examples the spike protein of the SARS-Cov-2 virus and a glycoprotein playing a role in the immune system (see [
3] for our earlier work). In
Section 4, the secondary structures are the musical forms of western music in the classical age and twentieth century music. Then, in
Section 5, the secondary structures in the verses of selected poems are obtained from an encoding of the types of words (names, verbs, prepositions, etc.).
A Brief Review of the Literature
After we received an invitation to contribute to the present special issue of Sci “Mathematics and poetry, with a view towards machine learning” we thought that our current group theoretical approach of protein language [
3] could be converted into an understanding of the poetic language, as well as an understanding of some musical structures.
Our goal in this subsection is to point out earlier work in the same direction as ours. There are many papers attempting to relate group theory to the genetic code, as reviewed in [
2] but we found none of them featuring the secondary structure of proteins along the chain of amino acids, as we did in [
3] and as we do below with the graph coverings.
Poetry inspired mathematics has been the common thread of most papers exploring the connection between poems and maths [
7,
8,
9,
10]. However, it is more challenging to explain what type of structure and beauty occurs in a poem in the language of mathematics [
11]. Perhaps mathematical linguistics is the proper frame for making progress [
12] and artificial intelligence (AI) may help in the classification of languages [
13].
Although both subjects have been connected for centuries, comparing musical structures to mathematics is a fairly new research domain [
14]. For a different perspective, the readers may consult Reference [
15].
2. Graph Coverings and Conjugacy Classes of a Finitely Generated Group
Let rel
be the relation defining the finitely presented group
on
r letters (or generators). We are interested in the conjugacy classes (cc) of subgroups of
with respect to the nature of the relation rel. In a nutshell, one observes that the cardinality structure
of conjugacy classes of subgroups of index
d of
is all the closer to that of the free group
on
generators as the choice of rel contains more non local structure. To arrive at this statement, we experiment on protein foldings, musical forms and poems. The former case was first explored in [
3].
Let
X and
be two graphs. A graph epimorphism (an onto or surjective homomorphism)
is called a covering projection if, for every vertex
of
,
maps the neighborhood of
bijectively onto the neighborhood of
. The graph
X is referred to as a base graph (or a quotient graph) and
is called the covering graph. The conjugacy classes of subgroups of index
d in the fundamental group of a base graph
X are in one-to-one correspondence with the connected
d-fold coverings of
X, as it has been known for some time [
16,
17].
Graph coverings and group actions are closely related.
Let us start from an enumeration of integer partitions of
d that satisfy:
a famous problem in analytic number theory [
18,
19]. The number of such partitions is
when
.
The number of
d-fold coverings of a graph
X of the first Betti number
r is ([
17], p. 41),
Another interpretation of Iso
is found in ([
20], Euqation (12)). Taking a set of mixed quantum states comprising
subsystems, Iso
corresponds to the stable dimension of degree
d local unitary invariants. For two subsystems,
and such a stable dimension is Iso
. A table for Iso
with small
d’s is in ([
17], Table 3.1, p. 82) or ([
20], Table 1).
Then, one needs a theorem derived by Hall in 1949 [
21] about the number
of subgroups of index
d in
to establish that the number Isoc
of connected
d-fold coverings of a graph
X (alias the number of conjugacy classes of subgroups in the fundamental group of
X) is as follows ([
17], Theorem 3.2, p. 84):
where
denotes the number-theoretic Möbius function.
Table 1 provides the values of Isoc
for small values of
r and
d ([
17], Table 3.2).
The finitely presented groups may be characterized in terms of a first Betti number r. For a group G, r is the rank (the number of generators) of the abelian quotient . To some extent, a group whose first Betti number is r may be said to be close to the free group since both of them have the same minimum number of generators.
4. Graph Coverings for Musical Forms
We accept that this structure determines the beauty in art. We provide two examples of this relationship, first by studying musical forms, then by looking at the structure of verses in poems. Our approach encompasses the orthodox view of periodicity or quasi-periodicity inherent to such structures. Instead of that and the non local character of the structure is investigated thanks to a group with generators given by the allowed generators and a relation rel, determining the position of such successive generators, as we did for the secondary structures of proteins.
4.1. The Sequence Isoc, the Golden Ratio and More
4.1.1. The Fibonacci Sequence
As shown in
Table 1, the sequence Isoc
only contains 1 in its entries and it is tempting to associate this sequence to the most irrational number, the Golden ratio
through the continued fraction expansion
.
Let us now take a two-letter alphabet (with letters
L and
S) and the Fibonacci words
defined as
,
,
. The sequence of Fibonacci words
is as follows
and its length corresponds to the Fibonacci numbers
.
Then, one can check that the finitely-presented group whose relation is a Fibonacci word possesses a cardinality sequence of subgroups equal to Isoc, up to all computable orders, despite the fact that the groups are not the same. It is straightforward to check that the first Betti number r of is 1, as expected.
4.1.2. The Period Doubling Cascade
Other rules lead to a Betti number
and the corresponding sequence Isoc(X;1). Let us consider the period-doubling cascade in the logistic map
. Period doubling can be generated by repeated use of the substitutions
and
., so that the sequence of period doubling is [
28]
and the corresponding finitely presented groups also have first Betti numbers equal to 1.
4.1.3. Musical Forms of the Classical Age
Going into musical forms, the ternary structure (most commonly denoted ) corresponding to the Fibonacci word is a Western instrumental genre notably used in sonatas, symphonies and string quartets. The basic elements of sonata forms are the exposition A, the development B and recapitulation A. While the musical form is symmetric, the Fibonacci word corresponding to is asymmetric and used in some songs or ballads from the Renaissance.
In a closely related direction, it was shown that the lengths
a and
b of sections
A and
B in all Mozart’s sonata movements are such that the ratio
[
29].
4.2. The Sequence Isoc in Twentieth Century Music and Jazz
In the 20th century, musical forms escaped the classical channels that were created. With the Hungarian composer Béla Bartók, a musical structure known as the arch form was created. The arch form is a sectional structure for a piece of music based on repetition, in reverse order, so that the overall form is symmetric, most often around a central movement. Formally, it looks like
. A well known composition of Bartok with this structure is
Music for strings, percussion and celesta [
30]. In
Table 4, it is shown that the cardinality sequence of cc of subgroups of the group generated with the relation rel=
corresponds to Isoc
up to the higher index 9 that we could check with our computer. A similar result is obtained with the symmetrical word
.
Our second example is a musical form known as twelve-bar blues [
31], one of the most prominent chord progressions in popular music and jazz. In this context, the notation
A is for the tonic,
B is for the subdominant and
C is for the dominant, each letter representing one chord. In twelve-bar blues, there are twelve chords arranged as in the first column of
Table 4. We observe that the standard twelve-bar blues are different in structure from the sequence of Isoc
. However, variations 1 and 2 have a structure close to Isoc
. In the former case, the first 9 orders lead to the same digit in the sequence.
Our third example is the musical form A-A-B-C-C. Notably, it is found in the
Slow movement from Haydn’s ‘Emperor quartet Opus 76, N°3 [
32] (
Figure 3), much sooner than the contemporary period. (See also Ref. [
33] for the frequent occurrence of the same musical form in djanba songs at Wadeye.) As in the aforementioned examples, the cardinality sequence of the cc of subgroups of the group built with rel=AABCC corresponds to Isoc
up to the highest index 9 that we could reach in our calculations.
Further musical forms with 4 letters A, B, C, and D and their relationship to Isoc
are provided in the lower part of
Table 4.
Not surprisingly, the rank
r of the abelian quotient of
is found to be 2 when the cardinality structure fits that Isoc
in
Table 4. Otherwise, the rank is 3. Similarly, the rank
r of the abelian quotient of
is found to be 3 when the cardinality structure fits that Isoc
in
Table 4. Otherwise, the rank is 4.
6. Conclusions
The graph covering approach has been shown to be useful for understanding how complex structures are encoded in nature and in art. For proteins, there exists a primary encoding with 20 amino acids as letters and the secondary encoding determines the folding of proteins in the 3-dimensional space. This is useful for recognizing the relationship between the structure and function of the protein. We took examples based on a present hot topic: a variant of the SARS-Cov-2 spike protein and the alipoprotein-H. For music, the secondary structures are called musical forms and the choice of them determines the type of music. For poems, we took the French (or English) alphabet with 26 letters, but many other alphabets may be used for the application of our approach. The secondary structures are defined from the encoding of the words (names, verbs and so on).
It is also interesting to speculate about the possible existence of a primary code and a secondary code in other fields, for example, in physics at the elementary level like in particle physics and quantum gravity [
35]. According to the experience of the authors of this paper, the structure has much to do with complete quantum information. The reader may consult paper [
36] about particle mixings or [
3,
37] about the genetic code in which finite groups are the players. Here, we are dealing with infinite groups so that the representation theory of finite groups (with characters) has to be defined on finitely-presented groups (most of the time of infinite cardinality). This will be explored further in our next paper [
38].