A Novel Approach of Heat Rate Enhancement in Rectangular Channels with Thin Porous Layer at the Channel Walls

Abstract

Heat transfer enhancement is a topic of great interest nowadays due to its different applications in industries. A porous material also known as metallic foam plays a major role in heat enhancement at the expense of pressure drop. The flow in channels demonstrates the usefulness of this technology in heat extraction. In our current study, a porous strip attached to the walls of the channels is proposed as an alternative for heat enhancement. The thickness of the porous strip was varied for different Reynolds numbers. By maintaining a laminar regime and using water as a fluid, we determined an optimum thickness of porous material leading to the highest performance evaluation criterion. In our current study, with the aspect ratio being the porous strip thickness over the channel width, an aspect ratio of 0.2 is found to be the alternative. A 40% increase in heat enhancement is detected in the presence of a porous strip when compared to a clear channel case for a Reynolds number equal to 200, which improves further as the Reynolds number increases accordingly.

1. Introduction

Heat transfer enhancement and heat storage are amongst the most studied topics in heat transfer. Ways to improve heat extraction received a large number of interests amongst researchers in this field [1]. Bayomy [2] in his Ph.D. study investigated experimentally and numerically porous rectangular channels and determined the thermal efficiency for different channel configurations. On one hand, porous media help heat extraction but at the expense of pressure drop. Welsford et al. [3] and Delisle et al. [4] investigated numerically and experimentally the use of nanofluid with different nanoparticles concentrations as a means to enhance heat extraction. They demonstrated that such an approach is feasible, but the pressure drop is noticeable as well. Plant et al. [5] extended the previous work by using hybrid fluid. In their experimental and numerical study, they demonstrated that adding copper helps enhance further the heat extraction, but the pressure drops keep increasing in magnitude; thus, more pumping power is needed. Different metallic foam permeabilities were used aiming at improving the thermal efficiency. Additional studies took place by other researchers within the Saghir group [6,7,8,9,10].

One of the major problems in using nanoparticles is the sedimentation in the bottom of the channels, making the pores in porous material blocked and thus defeating the purpose of using nanoparticles. Saghir and Rahman [11] were able to investigate this problem by including the Brownian motion and the thermophoretic effect. They were able to demonstrate an optimum flow rate to avoid having sedimentation in the channel. However, an innovative new approach which on one hand improves heat extraction and does not affect the pressure drop is proposed in the present paper.

Investigation of the thin porous layer around a pipe has been investigated by Ghadikolaie et al. [12]. An increase in the heat transferred rate of 20% has been reported. Similar work by T’Joen et al. [13] was conducted where they simulated a row of aluminum tubes that were wrapped with a thin layer of metallic foam. Their findings confirm that the existence of this foam layer help increases the heat transfer rate. In line with the numerical work started earlier, Al Salem et al. [14] conducted an experimental study of forced convection over a heated tube wrapped with a porous layer at the exterior wall. The presence of a porous layer augmented the heat transfer without affecting the pressure drop. Le Breton et al. [15] used a thin porous layer at the wall of a square cavity in the presence of natural convection. Their finding suggests that the porous layer reduced the upwind flow and led to a decrease in the convective heat transfer. A lack of investigation of a thin porous layer inside a square channel led the author to investigate this problem numerically and then experimentally.

In this paper, we propose an innovative and novel numerical approach in adding to a free channel wall a thin layer of porous foam. The goal is to continue to improve the heat enhancement without affecting the pressure drop. The novelty of the work is to be able to determine an optimum porous layer thickness to achieve the stated goal. Section 2 discusses the problem description followed by Section 3, where the finite element formulation and the applied boundary conditions are discussed. The mesh sensitivity is discussed in Section 4. To demonstrate the accuracy of the model, a comparison with experimental data is presented in Section 5. Section 6 presents the results obtained followed by the conclusion in Section 7.

2. Problem Descriptions

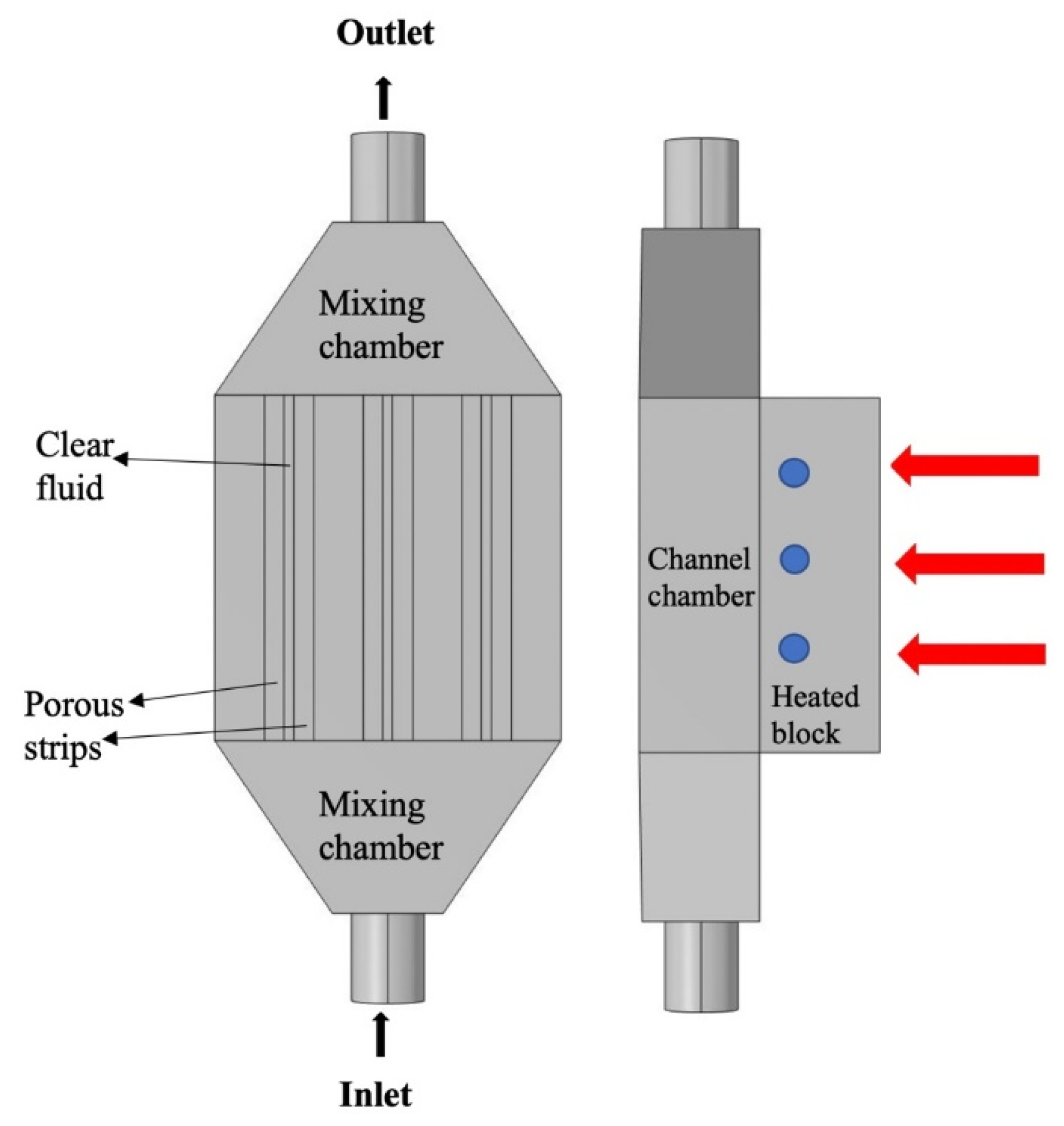
In the present study, efforts are made to investigate the importance of using different porous inserts in a rectangular channel. Enhancing heat removal by not disturbing the pressure drop is the main aim of this paper. Four different cases have been investigated in this paper. Figure 1 presents the model under investigation. This model has been investigated numerically and experimentally by different researchers [1,2,3,4,5] in the absence of porous foam or filled with porous foam. In the present study, the channels are plain, and a porous metallic foam strip having different thicknesses has been attached to its walls. In the previous study by Plant et al. [6], they demonstrated numerically and experimentally that nanofluid achieved a heat enhancement better than water.

However, nanofluids create larger pressure drops than water. It is the focus of this paper to figure out a means to improve heat extraction and maintaining a lower pressure drop by using water as the circulating fluid.

In Figure 1, two mixing chambers are present at the inlet and at the outlet, and the flow enters at a certain temperature Tin and certain flow rate. Temperature is measured 1 mm below the interface (see the blue dot), and the thermocouple is located at the middle of the heated block made of aluminum. The channel size is 0.00535 m in width and 0.0127 m in height. The block size containing the three channels, identified as channel chambers, is a square block of 0.0375 m inside made of aluminum as well. The red arrows show the heated element location where heat flux is applied to the adjacent metallic block.

At each channel, a strip of the porous layer is added, as shown in Figure 1. The strip is attached to the three wall surfaces of the corresponding channel, mainly the bottom side and the two left and right sides of the channel. The porous foam is made of the identical material as the channel, which is aluminum. Figure 2 presents the studied configuration for some aspect ratios. The aspect ratio is the ratio of the strip thickness over the width of the channel, which is maintained constant and equal to 0.00535 m. As the aspect ratio increases, the porous strip thickness increases accordingly. Thus, for an aspect ratio of 0.5, the channel is completely porous, and for an aspect ratio equal to zero, it is a clear fluid in a channel with no porous strip. With such configurations, in the presence of a porous strip, the flow will circulate in two places inside the channel. In the first place, flow penetration will be in the porous strip where the boundary and thermal layers are formed, and the second flow is in the clear path where there is no porous strip. Thus, as the aspect ratio increases from 0.1 to 0.5, the flow in the free channel is reduced, and more flow penetration exists in the porous area.

The reason for introducing this proposed design of porous strips is to be able to investigate the heat enhancement in a channel by reducing the large pressure drop observed experimentally and numerically. The flow is assumed to be laminar with a Reynolds number not exceeding 600. The questions that we raised from this analysis are first, whether the existence of a porous strip would lead to a better performance evaluation criterion than in the case of porous channels or clear channels, and secondly, whether there exists an optimum aspect ratio or porous thickness for high heat enhancement. These two questions will be addressed in the discussion section.

3. Finite Element Formulations and Boundary Condition

The full Navier–Stokes equation together with the energy equation was solved numerically using the finite element code COMSOL [16]. In addition, the heat conduction equation was also solved for the solid part of the model, which is mainly the channel walls as well as the heated block. Below, we present the formulation in non-dimensional form.

3.1. Fluid Flow Formulation

Using the following non-dimensional parameter

$$\mathrm{X}=\frac{\mathrm{x}}{\mathrm{D}}, \mathrm{Y}=\frac{\mathrm{y}}{\mathrm{D}}, \mathrm{Z}=\frac{\mathrm{z}}{\mathrm{D}}, \mathrm{U}=\frac{\mathrm{u}}{{\mathrm{u}}_{\mathrm{in}}}, \mathrm{V}=\frac{\mathrm{v}}{{\mathrm{u}}_{\mathrm{in}}}, \mathrm{W}=\frac{\mathrm{w}}{{\mathrm{u}}_{\mathrm{in}}},\mathrm{P}=\frac{\mathrm{pD}}{{\mathsf{\mu }\mathrm{u}}_{\mathrm{in}}}, \mathsf{\theta }=\frac{\left(\mathrm{T}-{\mathrm{T}}_{\mathrm{in}}\right)\mathrm{k}}{{\mathrm{q}}^{″}\mathrm{D}},$$

(1)

the non-dimensional terms obtained are

$$\mathrm{Re}=\frac{{\mathsf{\rho }\mathrm{u}}_{\mathrm{in}}\mathrm{D}}{\mathsf{\mu }}, \mathrm{and} \mathrm{Pr}=\frac{\mathrm{cp}\mathsf{\mu }}{\mathrm{k}}.$$

(2)

Here u_in is the velocity at the inlet, as shown in Figure 1. The conductivity is k, the pressure is p, the applied heat flux is q″ and T_in is the temperature at the inlet. The characteristic length D is taken equal to 0.01897 m, and Re and Pr are the Reynolds number and the Prandtl number of the fluid, which is water in the present study. The physical properties of the water are taken from the literature at room temperature.

The full Navier–Stokes equation in three dimensions are as follows.

X-direction

$$\mathrm{Re}\left[\mathrm{U}\frac{\partial \mathrm{U}}{\partial \mathrm{X}}+\mathrm{V}\frac{\partial \mathrm{U}}{\partial \mathrm{Y}}+\mathrm{W}\frac{\partial \mathrm{U}}{\partial \mathrm{Z}}\right]=-\frac{\partial \mathrm{P}}{\partial \mathrm{X}}+[\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{X}}^2}+\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{Y}}^2}+\frac{{\partial }^2\mathrm{U}}{\partial {\mathrm{Z}}^2}]$$

(3)

Y-direction

$$\mathrm{Re}\left[\mathrm{U}\frac{\partial \mathrm{V}}{\partial \mathrm{X}}+\mathrm{V}\frac{\partial \mathrm{V}}{\partial \mathrm{Y}}+\mathrm{W}\frac{\partial \mathrm{V}}{\partial \mathrm{Z}}\right]=-\frac{\partial \mathrm{P}}{\partial \mathrm{Y}}+[\frac{{\partial }^2\mathrm{V}}{\partial {\mathrm{X}}^2}+\frac{{\partial }^2\mathrm{V}}{\partial {\mathrm{Y}}^2}+\frac{{\partial }^2\mathrm{V}}{\partial {\mathrm{Z}}^2}]$$

(4)

Z-direction

$$\mathrm{Re}\left[\mathrm{U}\frac{\partial \mathrm{W}}{\partial \mathrm{X}}+\mathrm{V}\frac{\partial \mathrm{W}}{\partial \mathrm{Y}}+\mathrm{W}\frac{\partial \mathrm{W}}{\partial \mathrm{Z}}\right]=-\frac{\partial \mathrm{P}}{\partial \mathrm{Z}}+[\frac{{\partial }^2\mathrm{W}}{\partial {\mathrm{X}}^2}+\frac{{\partial }^2\mathrm{W}}{\partial {\mathrm{Y}}^2}+\frac{{\partial }^2\mathrm{W}}{\partial {\mathrm{Z}}^2}].$$

(5)

Here U, V, and W are the velocities at X, Y, and Z in non-dimensional form.

3.2. Energy Formulation

The energy equation for the fluid portion is as follows

$$\mathrm{RePr}\left[\mathrm{U}\frac{\partial \mathsf{\theta }}{\partial \mathrm{X}}+\mathrm{V}\frac{\partial \mathsf{\theta }}{\partial \mathrm{Y}}+\mathrm{W}\frac{\partial \mathsf{\theta }}{\partial \mathrm{Z}}\right]=\left[\frac{{\partial }^2\mathsf{\theta }}{\partial {\mathrm{X}}^2}+\frac{{\partial }^2\mathsf{\theta }}{\partial {\mathrm{Y}}^2}+\frac{{\partial }^2\mathsf{\theta }}{\partial {\mathrm{Z}}^2}\right].$$

(6)

The local Nusselt number is known as the ratio of the convective heat coefficient multiplied by the characteristic length over the water conductivity (i.e.,$\frac{\mathrm{hD}}{\mathrm{k}}$), so based on the non-dimensional adopted earlier, it becomes the inverse of the temperature. Thus

$$\mathrm{Nu}=\frac{1}{\mathsf{\theta }}.$$

(7)

The performance evaluation criteria PEC is taken as the ratio between the average Nusselt number and the pressure drop to the power 0.3333. Thus, the formulation for the PEC is as follows

$$\mathrm{PEC}=\left[\overline{\mathrm{Nu}}\right]/{\left[{\Delta }\mathrm{P}\right]}^{1/3}.$$

(8)

Here, $\overline{\mathrm{Nu}}$ is the average Nusselt number for the current case under investigation. Similarly, the pressure drops ${\Delta }\mathrm{P}$ is for the pressure drop between the inflow located at the center of the inlet mixing chamber and the center of the outlet mixing chamber.

3.3. Boundary Conditions

Figure 1 presents the boundary condition. The fluid enters with a temperature Tin, which in non-dimensional form is $\mathsf{\theta }$ set equal to 0 and an inlet velocity along the flow direction of 1 based on Equation (1). Three different Reynolds numbers of 200, 400, and 600 have been investigated corresponding to an inlet flow rate of 7.56 × 10⁻⁶ m³/s, 1.512 × 10⁻⁵ m³/s, and 2.268 × 10⁻⁵ m³/s, respectively. The flow rate is defined as the product of the inlet velocity multiplied by the cross-section area of the mixing chamber, which is 0.0127 m × 0.0375 m. The system is heated from the bottom with a heat flux having a unit non-dimensional value of 1. At the outlet location of the flow, a free boundary is applied. The entire external surfaces are assumed to be insulated to eliminate heat losses to the atmosphere.

4. Mesh Sensitivity Analysis and Convergence Criteria

The mesh sensitivity is examined to determine the optimal mesh required for the analysis. In

Table 1. Mesh information for different levels of meshing.

Coarse	126,890 domain elements, 17,200 boundary elements, 1489 edge elements
Normal	23,2918 domain elements, 25,988 boundary elements, 1859 edge elements
Fine	500,224 domain elements, 43,508 boundary elements, 2420 edge elements

, different mesh sizes were investigated following the terminology used by COMSOL software. The mesh levels that COMSOL supports and the element numbers for each mesh level are shown in Table 1. The average Nusselt number was evaluated at 1 mm below the interface in the aluminum block, and the results are represented in Figure 3a. A normal mesh level will be suitable to be used. Figure 3b presents the finite element mesh used in our simulation. Different approaches exist in COMSOL to tackle the convergence criteria. In this particular model, the default solver used was the segregated method. Details about this approach could be found in any finite element textbook. The convergence criterion is clearly explained in the COMSOL manual. In summary, the convergence criteria were set as follows: at every iteration, the average relative error of U, V, W, P, and $\mathsf{\theta }$ was computed. These were obtained using the following relation:

$${\mathrm{R}}_{\mathrm{c}}=\frac{1}{\mathrm{n} · \mathrm{m}}{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{m}}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{j}=\mathrm{n}}\left|\frac{({\mathrm{F}}_{\mathrm{i},\mathrm{j}}^{s+1}-{\mathrm{F}}_{\mathrm{i},\mathrm{j}}^s)}{{\mathrm{F}}_{\mathrm{i},\mathrm{j}}^{s+1}}\right|$$

(9)

where F represents one of the unknowns, viz. U, V, W, P, or $\mathsf{\theta }$, s is the iteration number, and (i, j) represents the coordinates on the grid. Convergence is reached if R_c for all the unknowns is below 1 × 10⁻⁶ in two successive iterations. For further information on the detailed solution method, the reader is referred to the COMSOL software manual [16].

5. Comparison with Experimental Data

Welsford et al. [3] and Plant and Saghir [5,6] conducted experimental measurement of temperature in three-channels configuration identical to the one shown in Figure 1. Concerning Welsford, the channels were filled with metallic foam, and the research conducted by Plant and Saghir had clear channels with no porous area. In both cases, water was circulating at different flow rates and heating conditions. Similar to our current cases, the temperatures were measured 1 mm below the interface, as shown in Figure 1.

Figure 4 presents a comparison between the measured experimental data and the calculated numerical data. The three channels contained a metallic foam insert having a permeability of 20 pores per square inch (20 PPI), which correspond to the permeability of 6.63304 × 10⁻⁴ m² and a porosity of 0.91. The flow rate is set equal to 0.2 US Gallon Per Minute (USPM), corresponding to a flow rate of 1.26 × 10⁻⁵ m³/s. The Reynolds number in this particular comparison is Re = 500, and the Prandtl number Pr is equal to 6.8358, in which water was the used fluid. As shown in Figure 4a, good agreement is achieved between the experimental and numerical data. As the flow circulates in the porous channel, the temperature increases accordingly. Figure 4b shows the comparison for the Nusselt number between experimental and numerical. Some discrepancies are observed in the results near the entrance of the channel for which the flow may not be fully developed yet. However, a good agreement is observed as well. One may conclude from these results that the model is well calibrated to investigate the proposed current configuration. However, one may need to compare with a clear channel case because the proposed model is a combination of porous strips and clear paths.

Additional comparison has been conducted with a similar case stated earlier but with free channels. Thus, the porous insert has been removed, allowing the flow to move freely, thus reducing the flow friction and the pressure drop. Plant and Saghir [5,6] conducted an experiment studying heat enhancement in a free channel. Water is used as a circulating fluid. The flow rate similar to the previous comparison was set at 0.2 US Gallon per Minute for different heat fluxes applied at the bottom of the heated plate. Similar configuration setup as the current model is foreseen. The Reynolds number for this case is set at 500. The inlet temperature was measured and found to be, depending on the heating condition, below 19 degrees Celsius. Figure 5 displays the comparison between the two cases: experimental and numerical. A good agreement is obtained between the two approaches. From Figure 4 and Figure 5, one may conclude that the numerical model is stable and accurate.

6. Results and Discussions

In the previous section, we have demonstrated the accuracy of our numerical model in predicting precisely the temperature and the Nusselt number when compared to measured experimental data in our lab. The rationale for choosing those two cases is because in our study, the insert is a combination of porous strip and free flow channel: thus, the novelty and uniqueness of our current studied model. From previous cases, we noticed that a porous medium can enhance the heat transfer at the expense of a large pressure drop. In contrast, the opposite is seen for the free channel, where heat enhancement is less than expected but with a lower pressure drop. Hence, in the present study, an attempt is made to study the optimum thickness of the porous material for better heat enhancement and a lower pressure drop.

Different cases have been investigated, and the key parameter between each case is the so-called aspect ratio AR. This aspect ratio is the ratio of the thickness of the porous strip to the channel width. With a constant channel width, the thickness of the porous strip varies from 0.000535 to 0.002675 m, which corresponds to an aspect ratio varying between 0.1 and 0.5, respectively. When the aspect ratio is set equal to 0.5, that means that the entire channels are filled with porous foam. Contrary, when the aspect ratio AR is set equal to 0, it means there is no porous strip in the channel, which is identified as a free channel.

Three different flow rates were investigated leading to a Reynolds number equal to 200, 400, and 600, respectively. For the porous strip, we have chosen a permeability of 20 pores per inch (i.e., 20PPI), which corresponds to a permeability equal to 6.63304 × 10⁻⁴ m² and a porosity of 0.91, which are identical to our current setup and similar to our experimental comparison.

Figure 6 presents the temperature variation, calculated, 1 mm below the interface for different aspect ratios from 0.1 to 0.5, respectively.

It is evident from the results in Figure 6 that as the aspect ratio increases, heat enhancement is noticeable. The temperature variation keeps dropping in magnitude as the porous material increases in the channels, meaning the flow is absorbing more heat. Another obvious observation is that as the flow rate increases, the temperature drops as expected. The positive slope of the temperature is an indication that as the flow circulates in the channel, heat extraction is less toward the end of the channel, leading to a rise in temperature. This is due to the development of the boundary layer and thus forcing less heat to be extracted. Another way to observe this heat extraction phenomenon is to display the Nusselt number variation along the flow path for different aspect ratios and flow rates, as depicted in Figure 7.

The variation trend of the Nusselt number regardless of the cases studied is similar. It is the inverse of the non-dimensional temperature as indicated earlier. In addition, it is evident that as the aspect ratio increases, the Nusselt number increases, as predicted. That means heat enhancement is more noticeable in the presence of porous material. The volume of porous material in the channel is increasing, leading to a better heat enhancement. The slope of the Nusselt number is a good indicator for the development of the thermal boundary layer at the entrance. As the flow progresses, the thickness of the boundary layer is increasing, not allowing heat to dissipate into the flow. It is believed that a combination of flow boundary layer and thermal boundary layer are implicated in heat dissipation to the fluid. Nevertheless, as the Reynolds number increases, the heat extraction increases accordingly.

Further investigation of the behavior is needed to combine these two effects. Figure 8 presents the pressure drop variation between the flow inlet and the flow outlet for all cases from an aspect ratio of 0 to an aspect ratio of 0.5. This pressure drop is a good indicator of the friction occurring during the flow in the channels. The position of the pressure drop is taken in the inlet mixing chamber and outlet mixing chamber, thus taking into consideration the three channels’ effect.

The presence of a porous strip regardless of its thickness (i.e., aspect ratio AR) generates a pressure drop larger than the case of the absence of a porous strip (i.e., AR = 0). However, it was noticed earlier that a porous strip enhances the heat extraction but at the expense of the pressure drop. However, as the flow rate represented by the Reynolds number increases, a slight decrease in the pressure drop is observed as the aspect ratio increases. There must be an optimum aspect ratio or in other words, porous strip thickness, which can, on one hand, enhance the heat transfer and two lower the pressure drops. Combining the findings, Figure 7, Figure 8 and Figure 9 present the performance evaluation criteria defined in Equation (8) for all cases.

One may observe that by combining the heat transfer enhancement and the flow behavior, we can achieve an optimum porous thickness that could be suitable for engineering application. As observed in Figure 9, with an increase in pressure drop due to the presence of porous strips, heat extraction is increasing as well. The performance evaluation criteria in Figure 9 show that there is an optimum thickness to be considered. In our current case, the optimum porous thickness corresponds to an aspect ratio of 0.2. Before and after this aspect ratio, the performance of the channel decreases. This observation is valid for different Reynolds numbers, as shown in Figure 9. Figure 10 presents the improvement percentage of the performance evaluation criteria when compared to the case of the clear channel. It is evident from Figure 10 that the best configuration is the one for an aspect ratio of 0.2. As the thickness of the porous layer increases, a drop in the improvement is noticeable. This observation applies to all Reynolds number cases.

7. Conclusions

In our current study, we focused our study on examining whether a porous strip in a channel can affect the extraction. Three channels of identical sizes were used, and a mixing chamber at the inlet and the outlet was modeled numerically using the finite element technique. By below the heating condition, the goal consisted of determining whether an optimum porous strip thickness can be determined for heat transfer enhancement. By comparing our numerical data with the current experiment for the case of free channels and porous channels, we demonstrated the accuracy of our model. In the present paper, the uniqueness of our study is the combination of porous material with free flow to determine the optimum porous thickness. The results revealed the following:

• The presence of a porous material in a channel leads to a noticeable heat extraction at the expense of pressure drop.
• A comparison between experimental data and numerical results showed the robustness of our numerical code.
• We have demonstrated that there is an optimum porous strip that can be used to extract the maximum heat for a minimum pressure drop. This optimum corresponds to an aspect ratio of 0.2.
• A maximum of 40% increase in performance evaluation criteria (PEC) is achieved for a Reynolds number equal to 200 and an aspect ratio of 0.2 when compared to the free channel. This improvement starts decreasing as the aspect ratio increase. The performance evaluation criteria increase as the Reynolds number increases to 400 and 600, which correspond to increases of 51% and 54%, respectively.