How Generic Is Eternal Inflation?
Abstract
:1. Introduction
1.1. Three Roads to Eternal Inflation
1.1.1. Stochastic Inflation
1.1.2. Long-Lived Metastable de Sitter Vacua
1.1.3. Inflating Topological Defects
1.2. The Case for Generic
1.3. The Dissent
1.4. Measures on Cosmologies
2. Monte Carlo Methods
2.1. Desperate Measures
2.1.1. Sampling Potential Functions
2.1.2. Sampling Initial Conditions
- A
- Sample field values maximizing , weighted by the distance in field space between the two adjacent minima. (This is equivalent to sampling uniformly and then going uphill to the peak.) Discard instances in which at .
- B
- Sample field values uniformly. Discard instances in which or at .
- C
- Sample field values a distance in field space equal to from local maxima of , weighted by the distance in field space between the two adjacent local minima. Discard instances in which or at .
Inflation Below the Peak
- A
- Sample field values maximizing , weighted by the distance in field space between the two adjacent minima. If at the peak, then assume inflation starts where first becomes valid , if along a trajectory approaching the peak as . (For details of the calculation, see Appendix A.)
2.2. Simulation Design
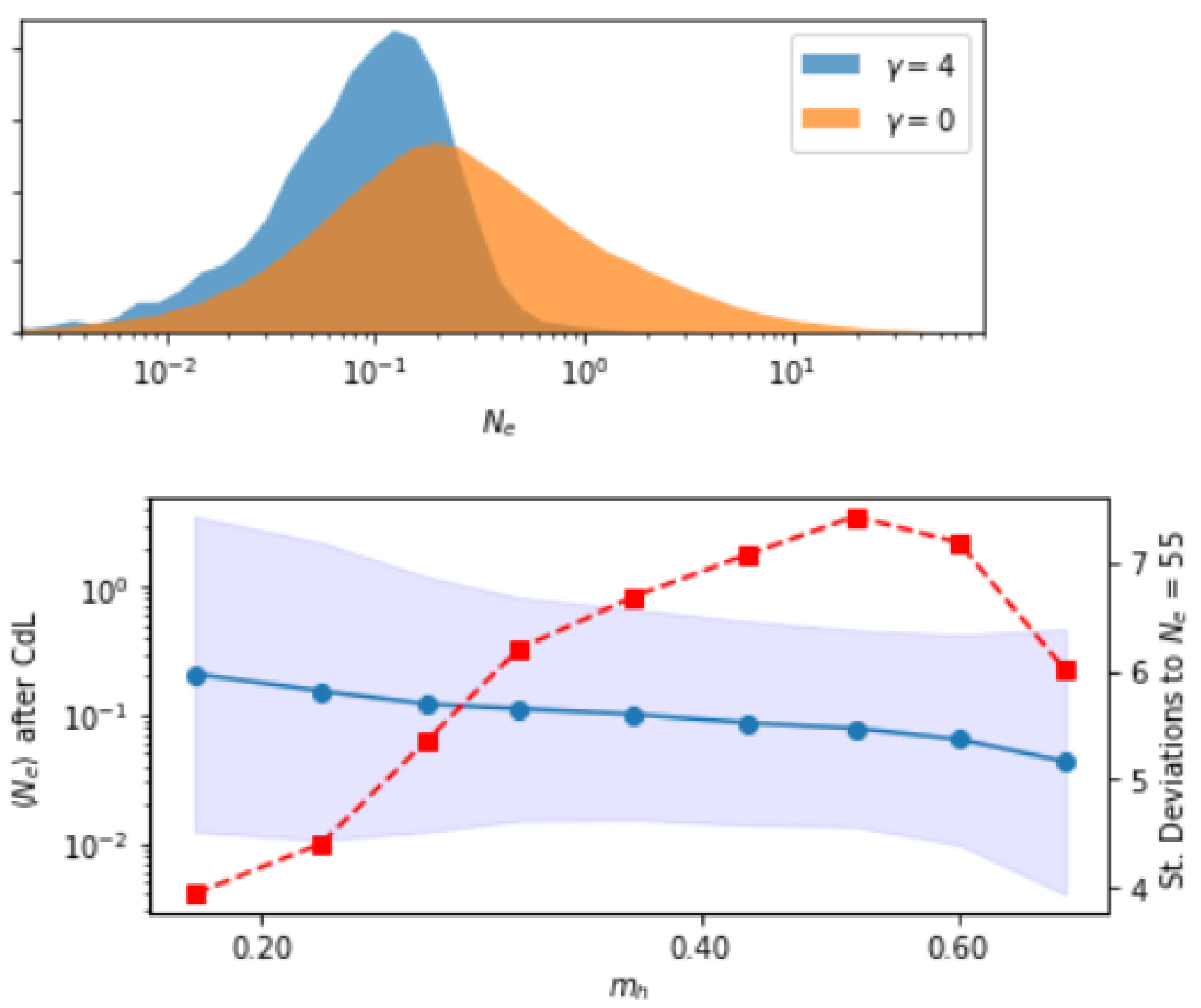
3. Results and Discussion
3.1. Measure A: Summits
- Let A denote the set of all models in the sample from Measure A.
- Let denote the set of models that have successful inflation, meaning greater than 70 e-folds accrued in an interval in which the potential slow roll conditions are satisfied.
- Let denote the set of models that are successful AND in which the only sustained bout of inflation occurs in a field space interval that is not contiguous with the peak.
- Let denote the set of models in D for which the stochastic inflation criteria are never satisfied. (All models in S but not in are stochastically eternal.)
3.1.1. Stochastic Eternality
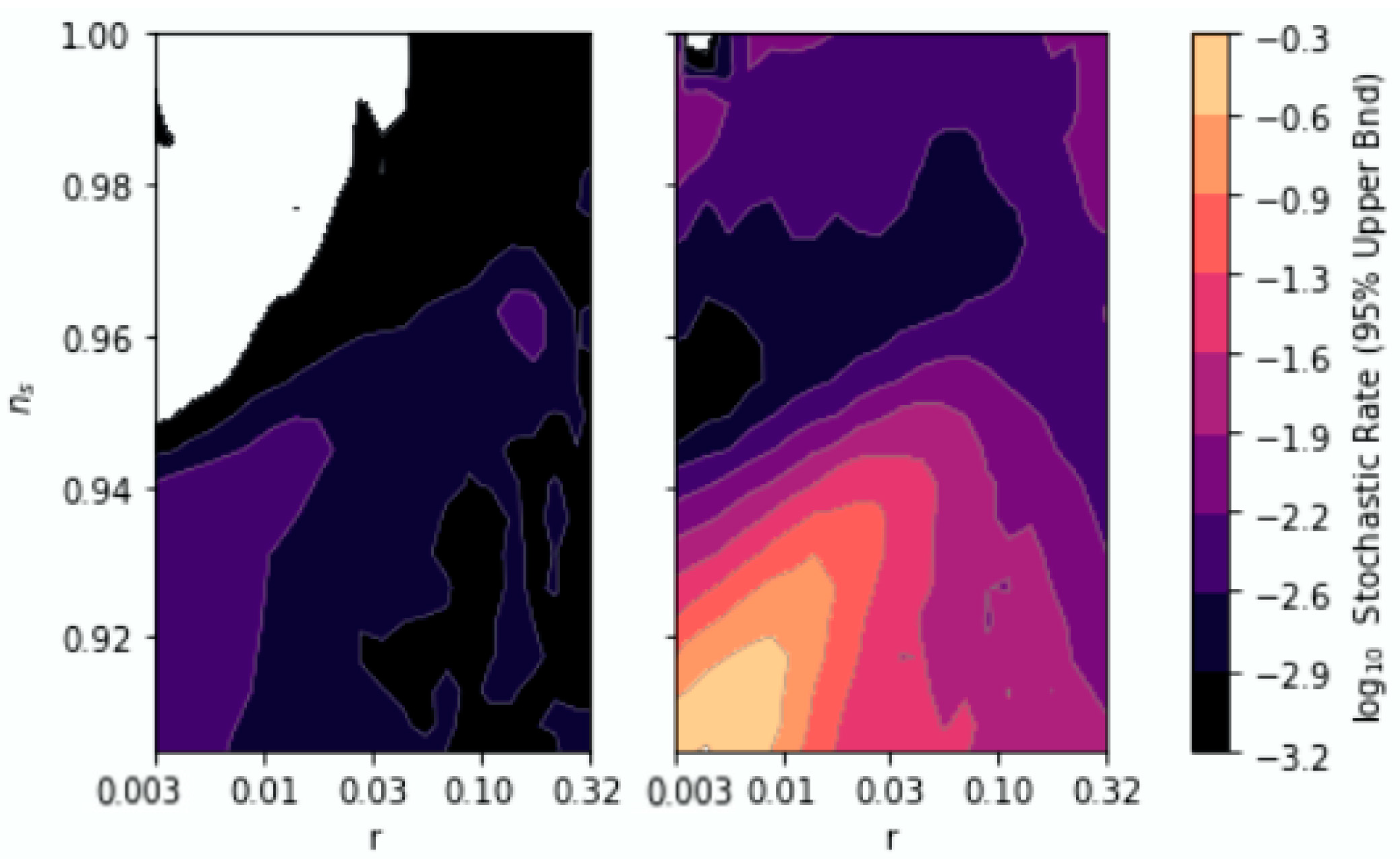
Conditioning on Spectral Shape
Conditioning on Spectral Amplitudes
3.1.2. Topological Eternality
3.2. Measure B: Uniform
3.2.1. Initialized in a True-Vacuum Basin
Stochastic Eternality
Topological Eternality
3.2.2. Initialized in a False-Vacuum Basin
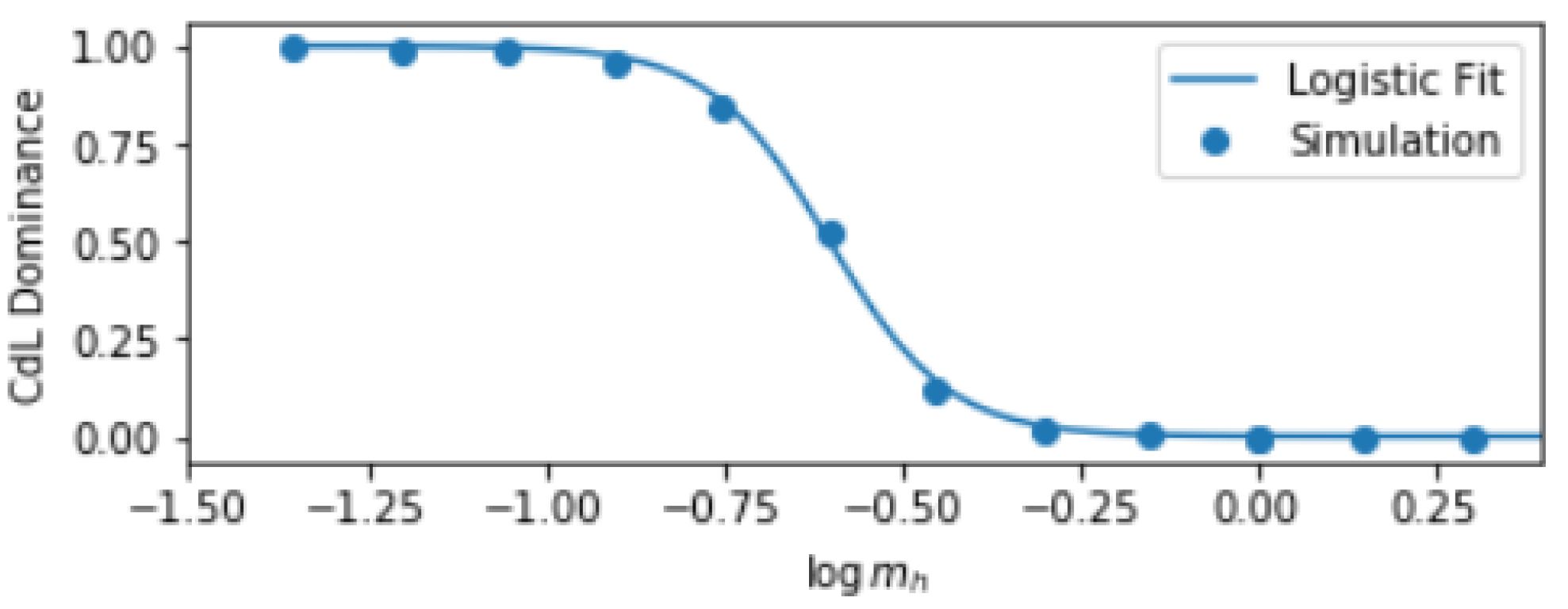
Coleman–de Luccia
Hawking–Moss
3.3. Measure C: Hilltops
4. Concluding Remarks
Further Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Monte Carlo Methods Continued
Appendix A.1. Simulation Design
- Initialization
- (a)
- (b)
- Initialize the inflaton at according to one of the Measures A, B, or C outlined above.
- (c)
- Determine the potential energy of the minimum of the starting basin and in one neighboring basin in both directions. (For Measure A, the starting basin adjacent to the initial peak is chosen randomly weighted by width.) If in any basin in this search space is below a threshold, shift the potential so that in that basin. If is negative and less than this threshold in the starting basin, abort.
- Instanton Pre-selectionComputing instanton profiles is time consuming, so we take the following steps to determine if a tunneling event is likely to be followed by sufficient inflation to produce a possibly observable universe in another basin of the potential.
- (a)
- If initialized in the true vacuum with , continue to Equation (4).
- (b)
- If the thin-wall or Hawking–Moss approximations hold, continue to Equation (3).
- (c)
- Taking the cutoff CDL instanton terminus on the true-vacuum side to coincide with , compute the maximum number of e-folds of inflation accrued over any field space interval in which the potential slow roll conditions are met between and the true minimum. If the maximum e-fold count is less than 70, abort.
- Check for Quantum Tunneling
- (a)
- If the thin-wall approximation is strongly valid or (Hawking–Moss eminent), compute the transition rate, otherwise
- (b)
- Compute the Coleman–de Luccia tunneling profile; determine the instanton terminus on the true-vacuum side; compute the number of e-folds of inflation, assuming inflation takes place anywhere below the terminus where the potential slow roll conditions are weakly met (.
- Characterize Slow Roll
- (a)
- Look downhill from for breakdown of the slow roll approximation, .
- (b)
- Compute the number of e-folds in the current basin. If , skip to Equation (6).
- (c)
- Find , the field value at the horizon exit scale for CMB fluctuations, taken to be 55 e-folds before the end of inflation. Our e-fold cutoffs (70 for successful inflation, 55 for imprinting of CMB fluctuations) of course depend on the fiducial reheating model. One could include those models in the input space, but we opt not to include that freedom in this analysis as doing so would likely obscure our conclusions.
- Check for Eternal Inflation
- (a)
- Evaluate the stochastic inflation criterion Equation (1) between and in each basin.
- (b)
- Check the second potential slow roll condition at all local maxima along the trajectory; compare to the upper bound for topological inflation.
- (c)
- If a transition into the basin with is followed by enough e-folds, compute the transition rate and compare to the upper bound in Equation (3).
- Data CollectionRecord observables if inflation ends with in a vacuum with , along with indicators for eternal inflation:
Appendix A.1.1. Criterion for Inflation Discontiguous with an Initial Peak

Appendix A.2. Instanton Computation
Appendix A.2.1. Instanton Pre-Selection
Appendix A.2.2. Obtaining the Profile
- Guess a starting field value on the true-vacuum side of the barrier.
- Integrate equations of motion for the scalar field and Euclidean radius of the bubble as a function of the radial coordinate .
- Stop integrating when one of the follow events occurs:
- (a)
- approaches with (Converge)
- (b)
- approaches 0 with or (Converge)
- (c)
- changes sign with (Undershoot)
- (d)
- passes (Overshoot)
- (e)
- approaches with (Converge) or (Overshoot)
- (f)
- changes sign (Converge)
- If converged, we’re done; return the profile.
- If within a tolerance value of the top the barrier, report a single data point that fully characterizes the Hawking–Moss profile.
- If the integration overshoots, move the guess closer to the maximum; if it undershoots, move the guess closer to the true minimum.
- Go to Step 2.
Appendix A.2.3. Transition Rates with Gravity
Appendix A.3. Statistical Methods
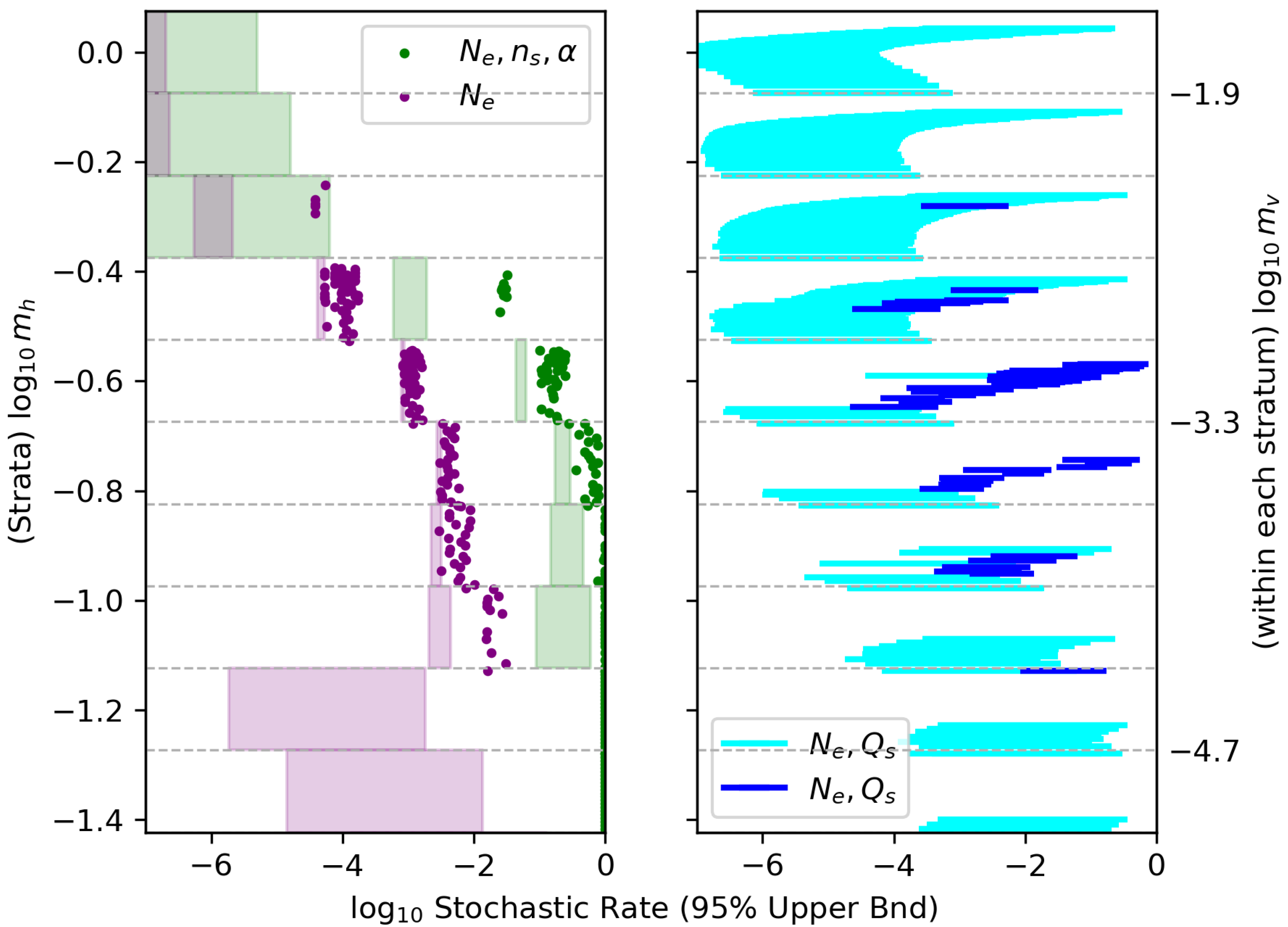
Appendix A.3.1. Mass Scale Weighting Schemes
- The epektacratic weighting scheme (rule by expansion) samples an equal number of potentials for each pairing of mass scales and , and lets them succeed or fail at producing sufficient e-folds of inflation. The total population is aggregated from successful inflation models at all mass scales, and that population is used to determine rates. Naturally this scheme will tend to give more representation to large field models.
- The democratic scheme gives every mass pairing within the specified range equal weight in informing in Equation (7), regardless of how common or rare it is for models comprising each to produce enough inflation. From each pairing, we sample as many potentials as it takes to get an equal number of successful models, or we give lower-expansion mass pairings extra weight to the same effect.
Appendix A.3.2. Rate Estimation

Appendix A.3.3. Testing Scale Invariance of Stochastic Eternal Inflation in Measure A
Appendix B. Matching Observables
Appendix B.1. Measure A

Appendix B.2. Measure B
Appendix B.3. Measure C
References
- Linde, A. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Guth, A.H. Eternal inflation and its implications. arXiv 2007, arXiv:hep-th/0702178. [Google Scholar] [CrossRef]
- Vilenkin, A. The Birth of Inflationary Universes. Phys. Rev. 1983, D27, 2848. [Google Scholar] [CrossRef]
- Aguirre, A. Eternal inflation, past and future. In Beyond the Big Bang; Vaas, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; Chapter 3. [Google Scholar]
- Olum, K.D. Is there any coherent measure for eternal inflation? Phys. Rev. D Part. Fields Gravit. Cosmol. 2012, 86, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, A.; Phillips, D. Origin of probabilities and their application to the multiverse. Phys. Rev. 2014, D90, 123514. [Google Scholar] [CrossRef] [Green Version]
- Aguirre, A.; Tegmark, M.; Layzer, D. Born in an Infinite Universe: A Cosmological Interpretation of Quantum Mechanics. Phys. Rev. 2011, D84, 105002. [Google Scholar] [CrossRef] [Green Version]
- Nomura, Y. Physical Theories, Eternal Inflation, and Quantum Universe. JHEP 2011, 11, 063. [Google Scholar] [CrossRef] [Green Version]
- Bousso, R.; Susskind, L. The Multiverse Interpretation of Quantum Mechanics. Phys. Rev. 2012, D85, 045007. [Google Scholar] [CrossRef] [Green Version]
- Tegmark, M. What does inflation really predict? J. Cosmol. Astropart. Phys. 2005, 4, 1. [Google Scholar] [CrossRef]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. 1981, D23, 347–356. [Google Scholar] [CrossRef] [Green Version]
- Coleman, S.R.; De Luccia, F. Gravitational Effects on and of Vacuum Decay. Phys. Rev. 1980, D21, 3305. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.; Moss, I. Fluctuations in the inflationary universe. Nucl. Phys. B 1983, 224, 180–192. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef] [PubMed]
- Batra, P.; Kleban, M. Transitions Between de Sitter Minima. Phys. Rev. D 2007, 76, 103510. [Google Scholar] [CrossRef] [Green Version]
- Mukhanov, V.F.; Abramo, L.R.W.; Brandenberger, R.H. On the Back reaction problem for gravitational perturbations. Phys. Rev. Lett. 1997, 78, 1624–1627. [Google Scholar] [CrossRef] [Green Version]
- Mersini-Houghton, L.; Parker, L. Eternal inflation is “Expensive”. arXiv 2007, arXiv:0705.0267. [Google Scholar]
- Parker, L. Amplitude of Perturbations from Inflation. arXiv 2007, arXiv:HEP-TH/hep-th/0702216. [Google Scholar]
- Nelson, E. Quantum Decoherence During Inflation from Gravitational Nonlinearities. JCAP 2016, 1603, 22. [Google Scholar] [CrossRef]
- Boddy, K.K.; Carroll, S.M.; Pollack, J. How Decoherence Affects the Probability of Slow-Roll Eternal Inflation. Phys. Rev. 2017, D96, 023539. [Google Scholar] [CrossRef] [Green Version]
- Kinney, W.H.; Freese, K. Negative running can prevent eternal inflation. J. Cosmol. Astropart. Phys. 2015, 2015. [Google Scholar] [CrossRef]
- Rudelius, T. Conditions for (no) eternal inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 9. [Google Scholar] [CrossRef] [Green Version]
- Liddle, A.; Lyth, D. Cosmological Inflation and Large-Scale Structure; Cosmological Inflation and Large-scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Greenwood, R. Eternal Inflation Monte Carlo. 2022. Available online: https://github.com/rossngreenwood/eternal_inflation/commit/52380a7fc7942f28f5c6217eed45332ad6436db5 (accessed on 25 May 2022).
- Hartle, J.B.; Hawking, S.W. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Wainwright, C.L. CosmoTransitions: Computing Cosmological Phase Transition Temperatures and Bubble Profiles with Multiple Fields. Comput. Phys. Commun. 2012, 183, 2006–2013. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greenwood, R.; Aguirre, A. How Generic Is Eternal Inflation? Sci 2022, 4, 23. https://doi.org/10.3390/sci4020023
Greenwood R, Aguirre A. How Generic Is Eternal Inflation? Sci. 2022; 4(2):23. https://doi.org/10.3390/sci4020023
Chicago/Turabian StyleGreenwood, Ross, and Anthony Aguirre. 2022. "How Generic Is Eternal Inflation?" Sci 4, no. 2: 23. https://doi.org/10.3390/sci4020023
APA StyleGreenwood, R., & Aguirre, A. (2022). How Generic Is Eternal Inflation? Sci, 4(2), 23. https://doi.org/10.3390/sci4020023




