Effect of Sweep on Axial Fan Noise Sources Using the Lattice Boltzmann Method
Abstract
:1. Introduction
2. Experimental Background
2.1. Configuration Description
2.2. Experimental Database

3. Numerical Investigation
3.1. Numerical Setup
3.2. Numerical Results
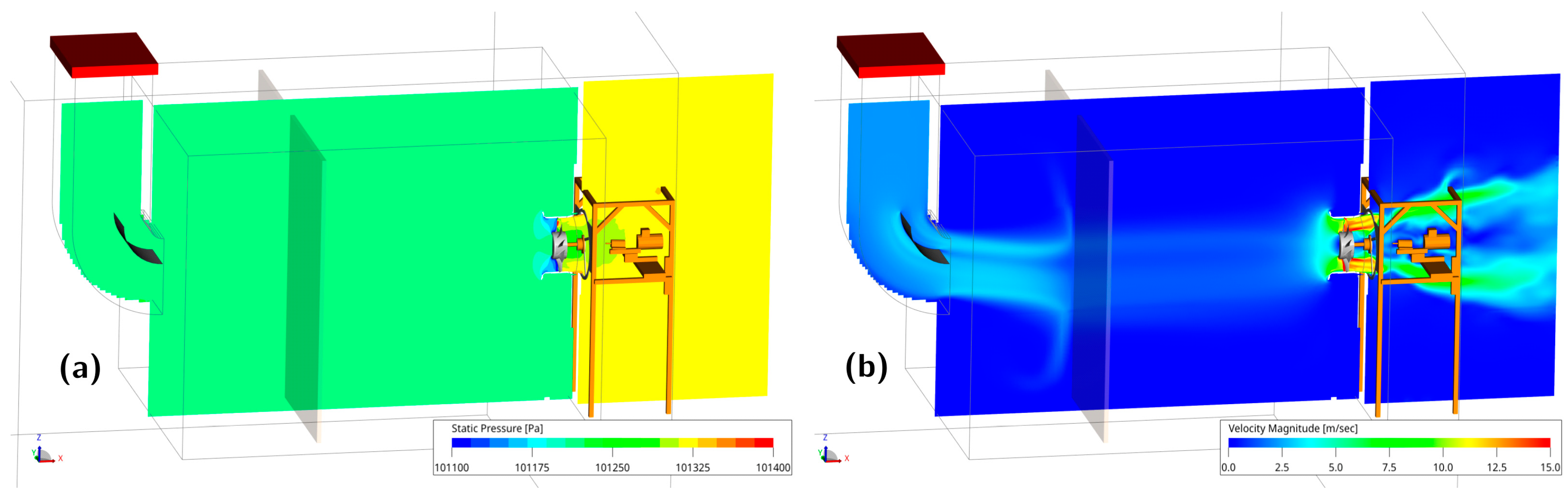
3.2.1. Aerodynamic Results
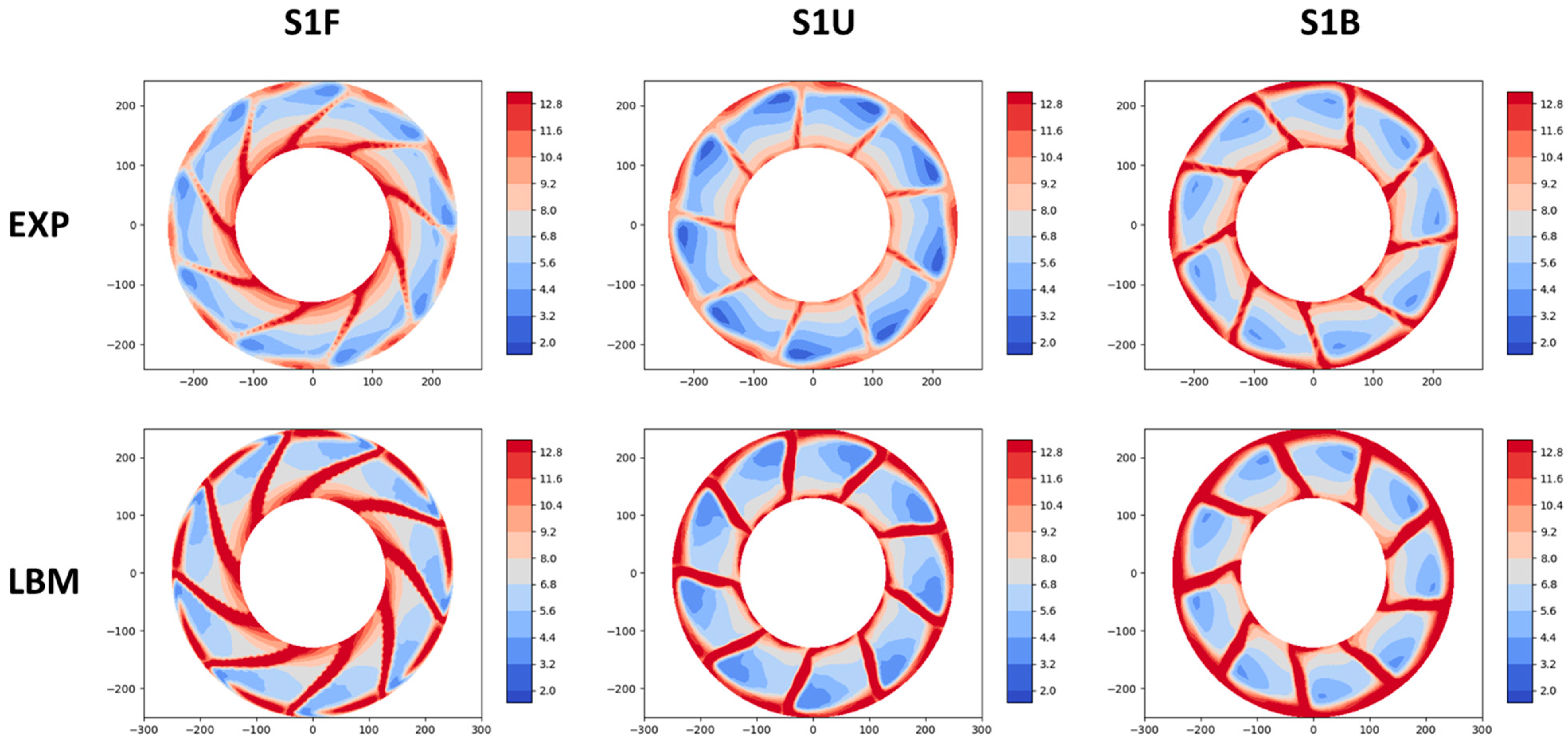
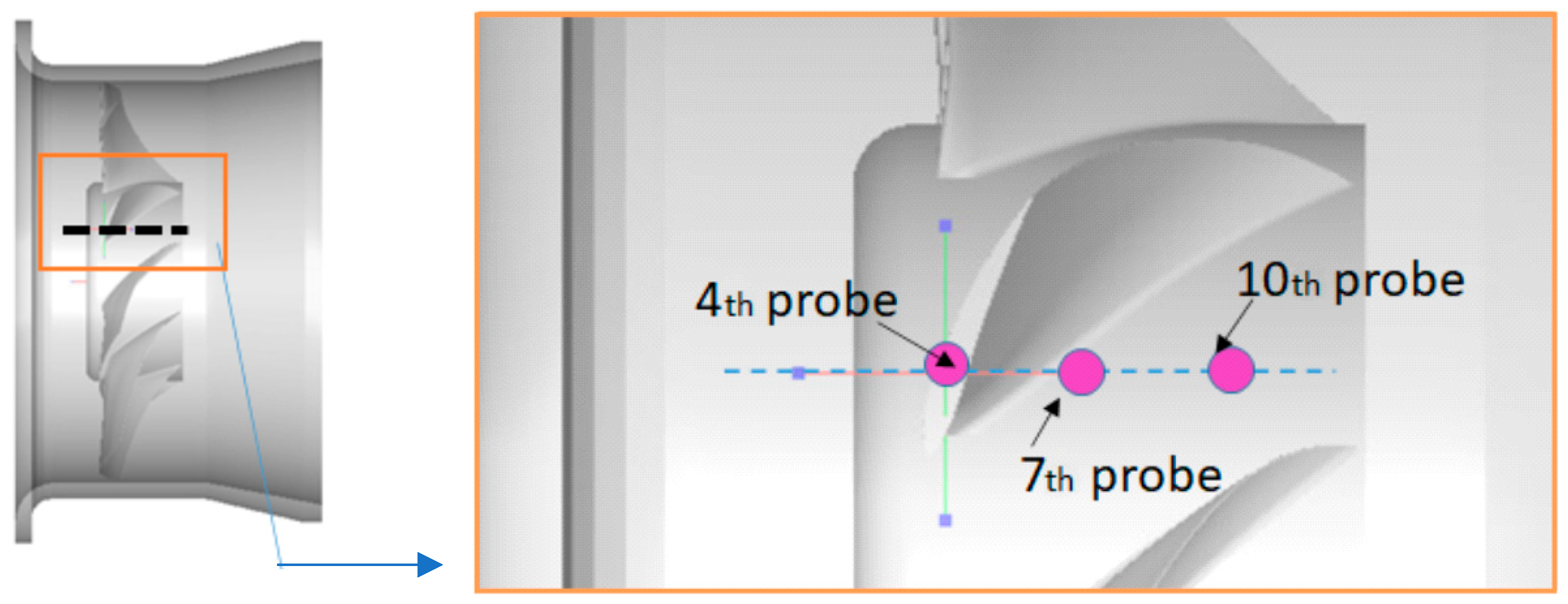
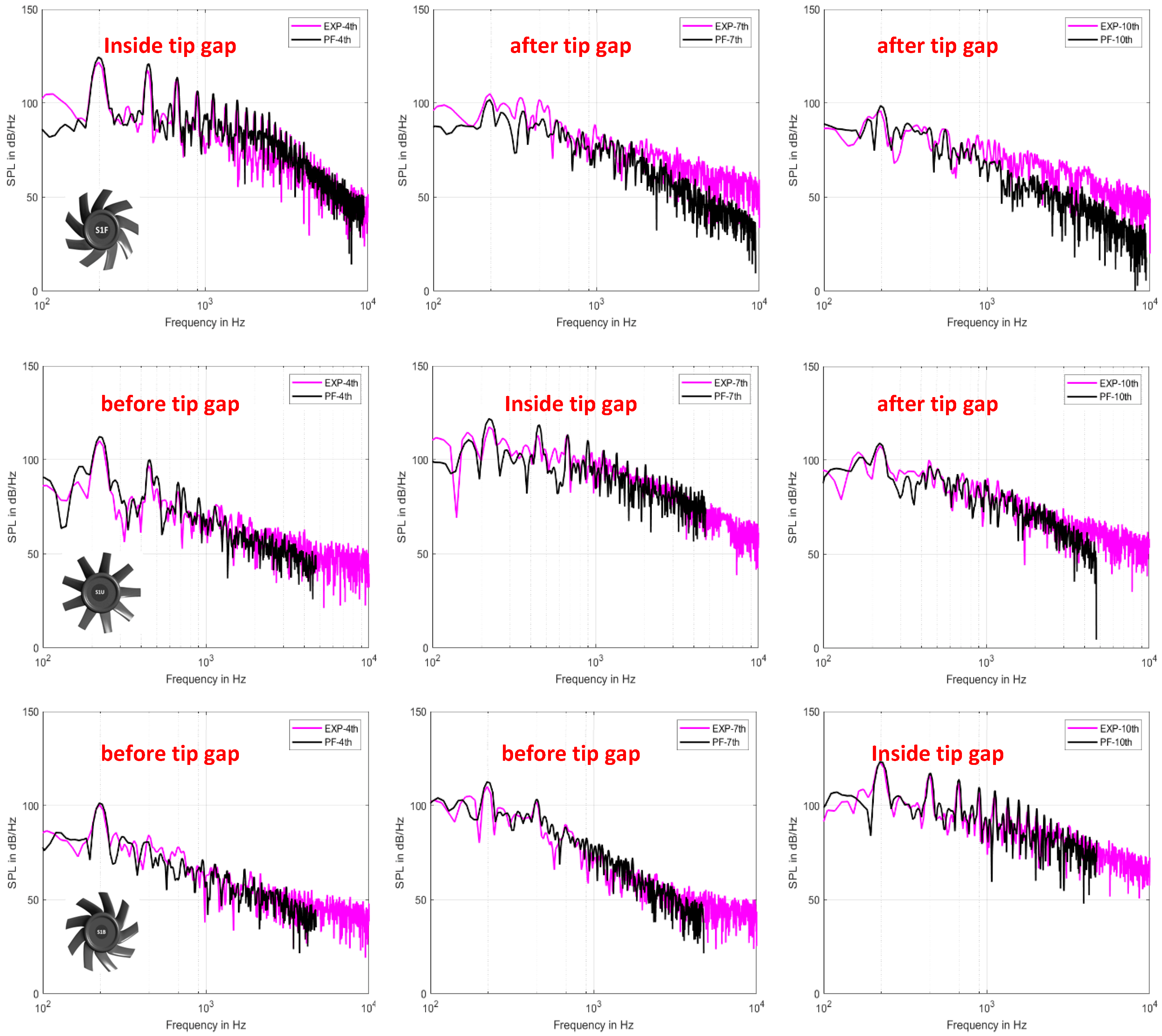
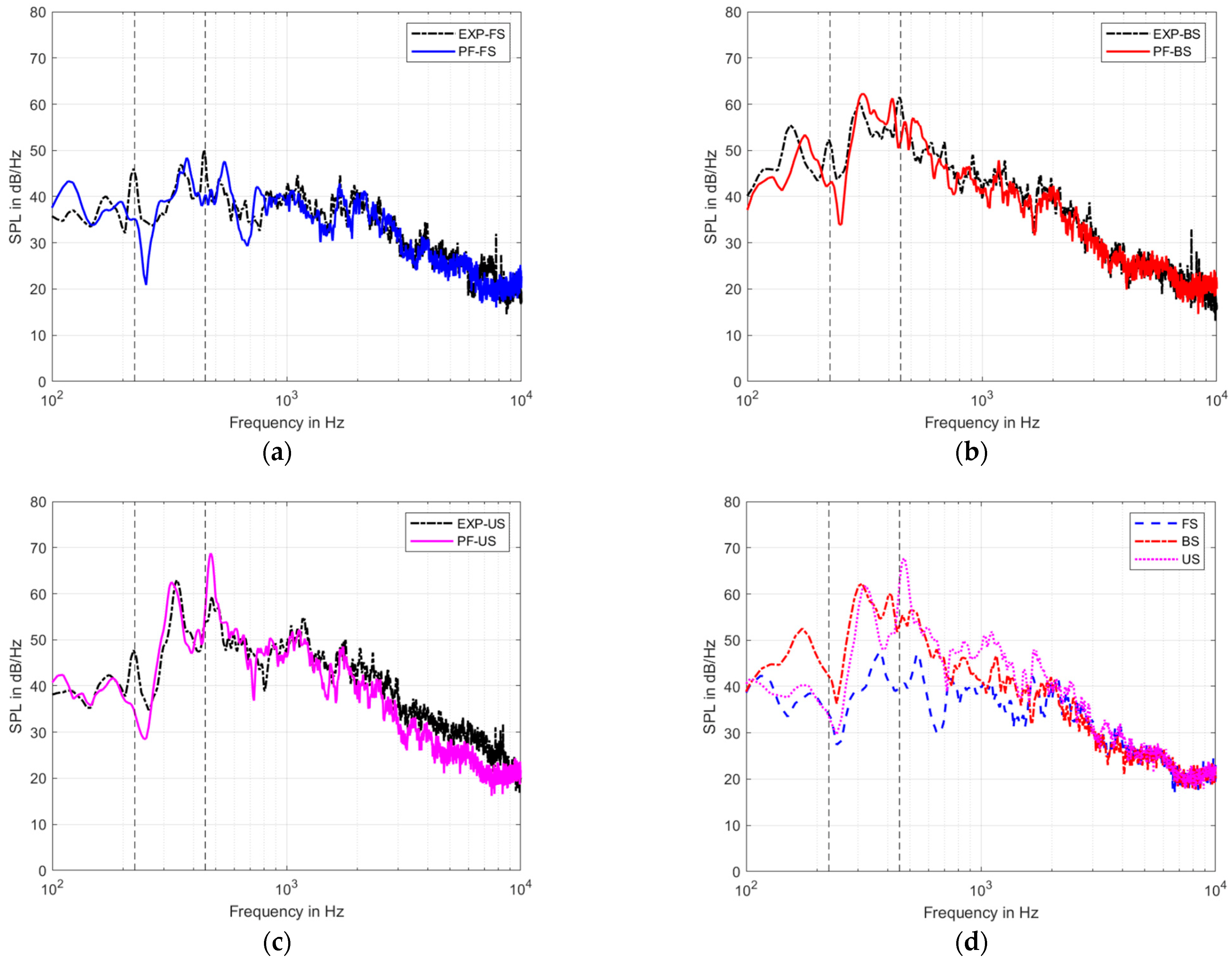
3.2.2. Acoustical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moreau, S. A Review of Turbomachinery Noise: From Analytical Models to High-Fidelity Simulations. In Fundamentals of High Lift for Future Civil Aircraft; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Carolus, T.; Beiler, M. Skewed blades in low pressure fans—A survey of noise reduction mechanisms, AIAA 97-1591 paper. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997. [Google Scholar]
- Grasso, G.; Roger, M.; Moreau, S. Analytical model of the source and radiation of sound from the trailing edge of a swept airfoil. J. Sound Vib. 2021, 493, 115838. [Google Scholar] [CrossRef]
- Krömer, F.J.; Moreau, S.; Becker, S. Experimental investigation of the interplay between the sound field and the flow field in skewed low-pressure axial fans. J. Sound Vib. 2019, 442, 220–236. [Google Scholar] [CrossRef]
- Zarri, A.; Christophe, J.; Moreau, S.; Schram, C. Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans. Acoustics 2021, 2, 812–832. [Google Scholar] [CrossRef]
- Pérot, F.; Kim, M.S.; Moreau, S.; Henner, M.; Neal, D. Direct Aeroacoustics Prediction of a Low Speed Axial Fan, AIAA 2010- paper. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010. [Google Scholar]
- Moreau, S. Direct Noise Computation of Low-speed Ring Fans. Acta Acust. United Acust. 2019, 105, 30–42. [Google Scholar] [CrossRef]
- Zenger, F. Sound Emission of Low-Pressure Axial Fans under Distorted Inflow Conditions. Ph.D. Thesis, Friedrich-Alexander-Universität, Erlangen, Germany, 2017. [Google Scholar]
- Herold, G.; Zenger, F.; Sarradj, E. Influence of blade skew on axial fan component noise. Int. J. Aeroacoustics 2017, 16, 418–430. [Google Scholar] [CrossRef]
- Schoder, S.; Junger, C.; Kaltenbacher, M. Computational aeroacoustics of the EAA benchmark case of an axial fan. Acta Acust. 2020, 4, 22. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Teixeira, C.; Molvig, K. Realization of Fluid Boundary Conditions via Discrete Boltzmann Dynamics. Int. J. Mod. Phys. C 1998, 9, 1281–1292. [Google Scholar] [CrossRef]
- Chen, H.; Orszag, S.A.; Staroselsky, I.; Succi, S. Expanded analogy between Boltzmann kinetic theory of fluids and turbulence. J. Fluid Mech. 2004, 519, 301–314. [Google Scholar] [CrossRef]
- Fares, E. Unsteady flow simulation of the Ahmed reference body using a lattice Boltzmann approach. Comput. Fluids 2006, 35, 940–950. [Google Scholar] [CrossRef]
- Avallone, F.; van der Velden, W.C.P.; Ragni, D.; Casalino, D. Noise reduction mechanisms of sawtooth and combed-sawtooth trailing-edge serrations. J. Fluid Mech. 2018, 848, 560–591. [Google Scholar] [CrossRef] [Green Version]
- Marié, S. Etude de la Méthode Boltzmann sur Réseau pour les Simulations en Aéroacoustique. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2008. [Google Scholar]
- Moreau, S.; Sanjose, M. Sub-harmonic broadband humps and tip noise in low-speed ring fans. J. Acoust. Soc. Am. 2016, 139, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.E.F.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Phil. Trans. R. Soc. Lond. 1969, 264, 321–342. [Google Scholar]
- Sturm, M.; Sanjosé, M.; Moreau, S.; Carolus, T. Aeroacoustic Simulation of an Axial Fan including the Full Test Rig by using the Lattice Boltzmann Method. In Proceedings of the Fan 2015 Conference, Lyon, France, 15–17 April 2015. [Google Scholar]
- Magne, S.; Moreau, S.; Berry, A. Subharmonic tonal noise from backflow vortices radiated by low-speed ring rotor in uniform inlet flow. J. Acous. Soc. Am. 2015, 137, 198–225. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Lallier-Daniels, D.; Sanjosé, M.; Moreau, S.; Carolus, T. Rotating coherent flow structures as a source for narrowband tip clearance noise from axial fans. J. Sound Vib. 2018, 417, 198–225. [Google Scholar] [CrossRef]
- Kameier, F.; Neise, W. Experimental Study of Tip Clearance Losses and Noise in Axial Turbomachines and Their Reduction. J. Turbomach. 1997, 119, 460–471. [Google Scholar] [CrossRef]
- Sanjose, M.; Moreau, S. RANS based analytical modeling of broadband noise for a low-speed fan. J. Acous. Soc. Am. 2018, 143, 198–225. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Ghodake, D.; Sanjosé, M.; Moreau, S.; Henner, M. Effect of Sweep on Axial Fan Noise Sources Using the Lattice Boltzmann Method. Int. J. Turbomach. Propuls. Power 2022, 7, 34. https://doi.org/10.3390/ijtpp7040034
Ghodake D, Sanjosé M, Moreau S, Henner M. Effect of Sweep on Axial Fan Noise Sources Using the Lattice Boltzmann Method. International Journal of Turbomachinery, Propulsion and Power. 2022; 7(4):34. https://doi.org/10.3390/ijtpp7040034
Chicago/Turabian StyleGhodake, Dipali, Marlène Sanjosé, Stéphane Moreau, and Manuel Henner. 2022. "Effect of Sweep on Axial Fan Noise Sources Using the Lattice Boltzmann Method" International Journal of Turbomachinery, Propulsion and Power 7, no. 4: 34. https://doi.org/10.3390/ijtpp7040034
APA StyleGhodake, D., Sanjosé, M., Moreau, S., & Henner, M. (2022). Effect of Sweep on Axial Fan Noise Sources Using the Lattice Boltzmann Method. International Journal of Turbomachinery, Propulsion and Power, 7(4), 34. https://doi.org/10.3390/ijtpp7040034







