Photons as Probes of Gluon Saturation in Dilute + Dense Collisions †
Abstract
:1. Introduction
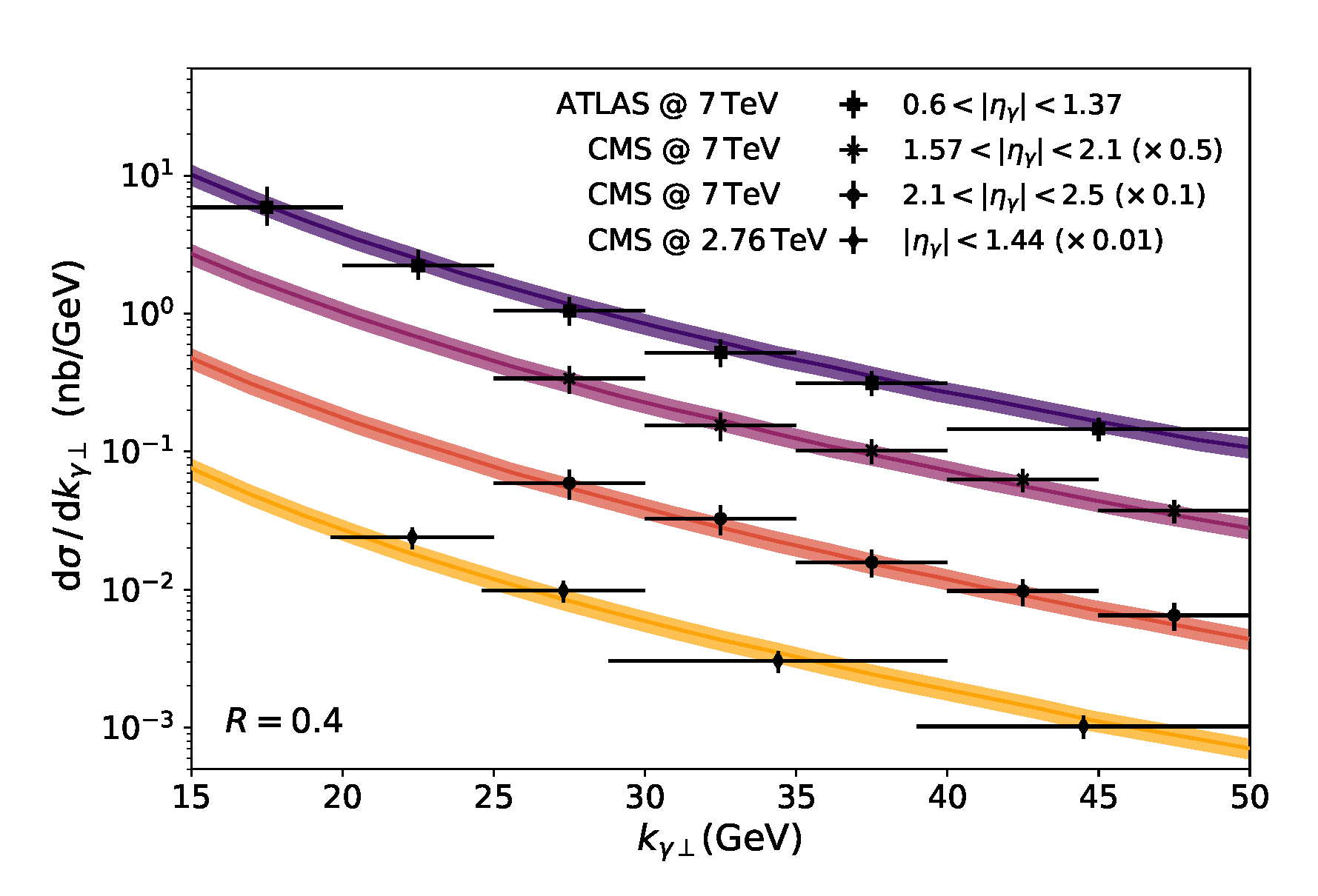
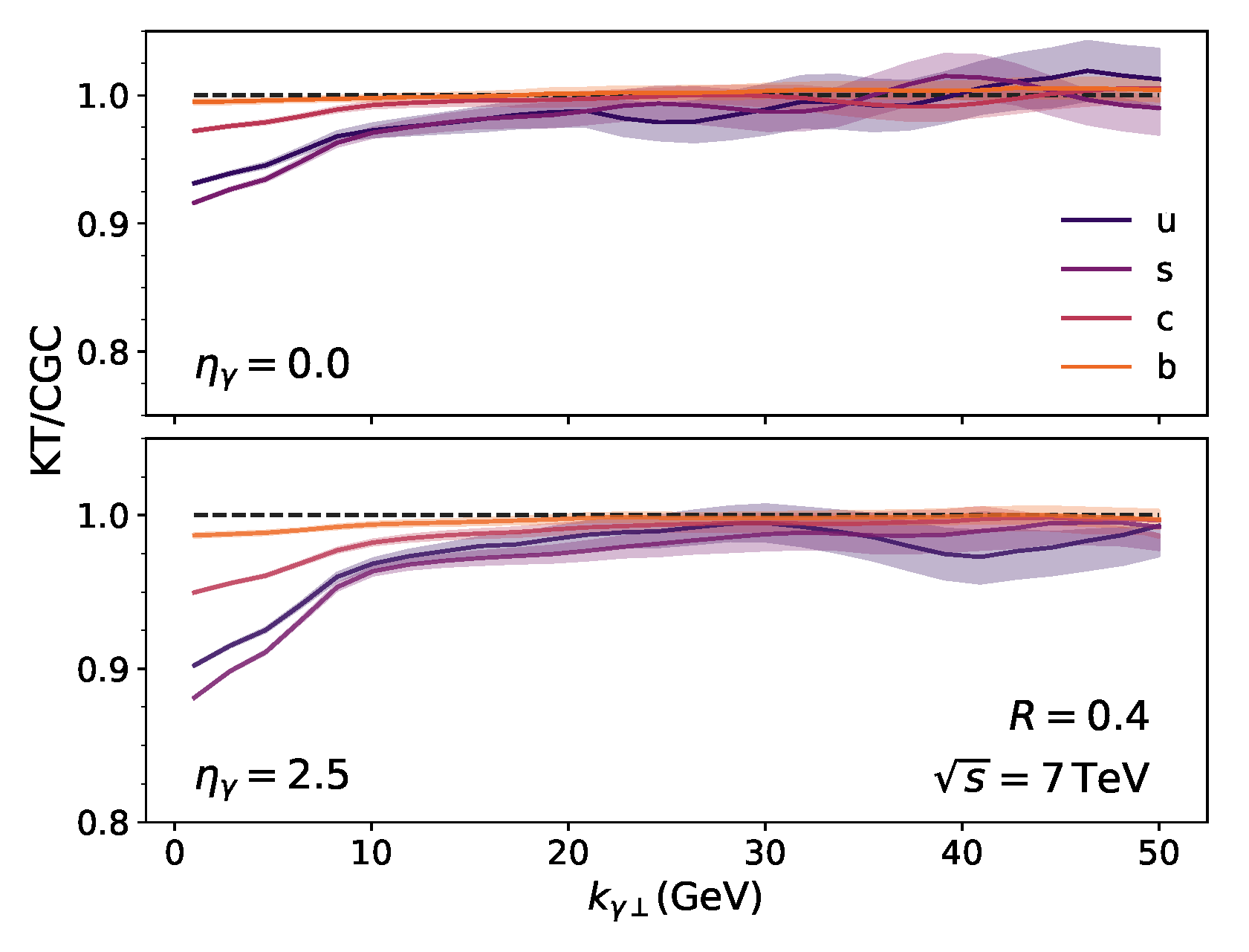
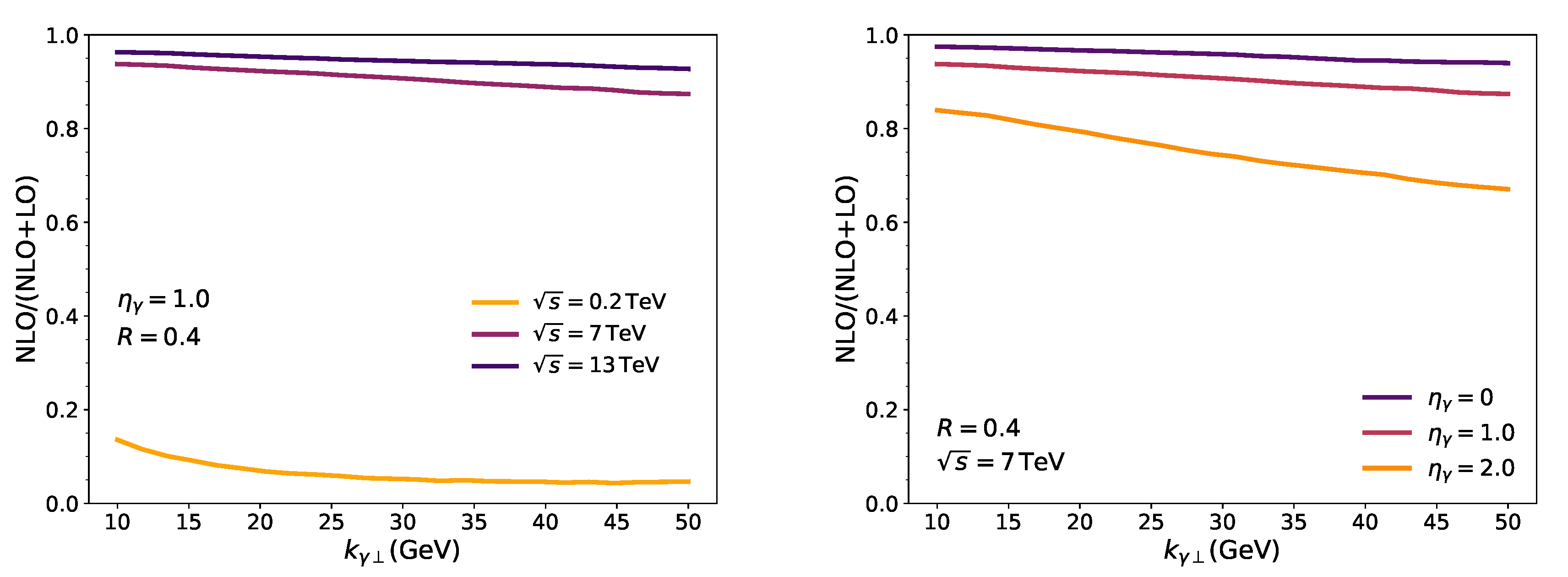
2. Results
3. Conclusions
Acknowledgments
References
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463. [Google Scholar] [CrossRef]
- Gelis, F.; Jalilian-Marian, J. Photon production in high-energy proton nucleus collisions. Phys. Rev. D 2002, 66, 014021. [Google Scholar] [CrossRef]
- Kopeliovich, B.; Tarasov, A.; Schafer, A. Bremsstrahlung of a quark propagating through a nucleus. Phys. Rev. C 1999, 59, 1609. [Google Scholar] [CrossRef]
- Benic, S.; Fukushima, K.; Garcia-Montero, O.; Venugopalan, R. Probing gluon saturation with next-to-leading order photon production at central rapidities in proton-nucleus collisions. JHEP 2017, 1701, 115. [Google Scholar] [CrossRef]
- Benic, S.; Fukushima, K. Photon from the annihilation process with CGC in the pA collision. Nucl. Phys. A 2017, 958, 1. [Google Scholar] [CrossRef]
- Benić, S.; Fukushima, K.; Garcia-Montero, O.; Venugopalan, R. Constraining unintegrated gluon distributions from inclusive photon production in proton-proton collisions at the LHC. Phys. Lett. B 2019, 791, 11–16. [Google Scholar] [CrossRef]
- Frixione, S. Isolated photons in perturbative QCD. Phys. Lett. B 1998, 429, 369. [Google Scholar] [CrossRef]
- d’Enterria, D.; Rojo, J. Quantitative constraints on the gluon distribution function in the proton from collider isolated-photon data. Nucl. Phys. B 2012, 860, 311. [Google Scholar] [CrossRef]
- Pumplin, J.; Stump, D.; Huston, J.; Lai, H.; Nadolsky, P.; Tung, W. New generation of parton distributions with uncertainties from global QCD analysis. JHEP 2002, 0207, 012. [Google Scholar] [CrossRef]
- Dusling, K.; Gelis, F.; Lappi, T.; Venugopalan, R. Long range two-particle rapidity correlations in A+A collisions from high energy QCD evolution. Nucl. Phys. A 2010, 836, 159. [Google Scholar] [CrossRef]
- Ma, Y.; Venugopalan, R. Comprehensive Description of J/Ψ Production in Proton-Proton Collisions at Collider Energies. Phys. Rev. Lett. 2014, 113, 192301. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Tribedy, P.; Venugopalan, R.; Watanabe, K. Event engineering studies for heavy flavor production and hadronization in high multiplicity hadron-hadron and hadron-nucleus collisions. Phys. Rev. D 2018, 98, 074025. [Google Scholar] [CrossRef]
- CMS Collaboration. Measurement of isolated photon production in pp and PbPb collisions at =2.76 TeV. Phys. Lett. B 2012, 710. [Google Scholar]
- ATLAS Collaboration. Measurement of the inclusive isolated prompt photon cross section in pp collisions at =7 TeV with the ATLAS detector. Phys. Rev. D 2011, 83, 052005. [Google Scholar] [CrossRef]
- CMS Collaboration. Measurement of the Differential Cross Section for Isolated Prompt Photon Production in pp Collisions at 7 TeV. Phys. Rev. D 2011, 84, 052011. [Google Scholar] [CrossRef]
| 1 | For the NLO channel, one needs to insert two isolation cuts. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benić, S.; Fukushima, K.; Garcia-Montero, O.; Venugopalan, R. Photons as Probes of Gluon Saturation in Dilute + Dense Collisions. Proceedings 2019, 10, 33. https://doi.org/10.3390/proceedings2019010033
Benić S, Fukushima K, Garcia-Montero O, Venugopalan R. Photons as Probes of Gluon Saturation in Dilute + Dense Collisions. Proceedings. 2019; 10(1):33. https://doi.org/10.3390/proceedings2019010033
Chicago/Turabian StyleBenić, Sanjin, Kenji Fukushima, Oscar Garcia-Montero, and Raju Venugopalan. 2019. "Photons as Probes of Gluon Saturation in Dilute + Dense Collisions" Proceedings 10, no. 1: 33. https://doi.org/10.3390/proceedings2019010033
APA StyleBenić, S., Fukushima, K., Garcia-Montero, O., & Venugopalan, R. (2019). Photons as Probes of Gluon Saturation in Dilute + Dense Collisions. Proceedings, 10(1), 33. https://doi.org/10.3390/proceedings2019010033