Locating the QCD Critical Point Using Holographic Black Holes †
Abstract
:1. Introduction
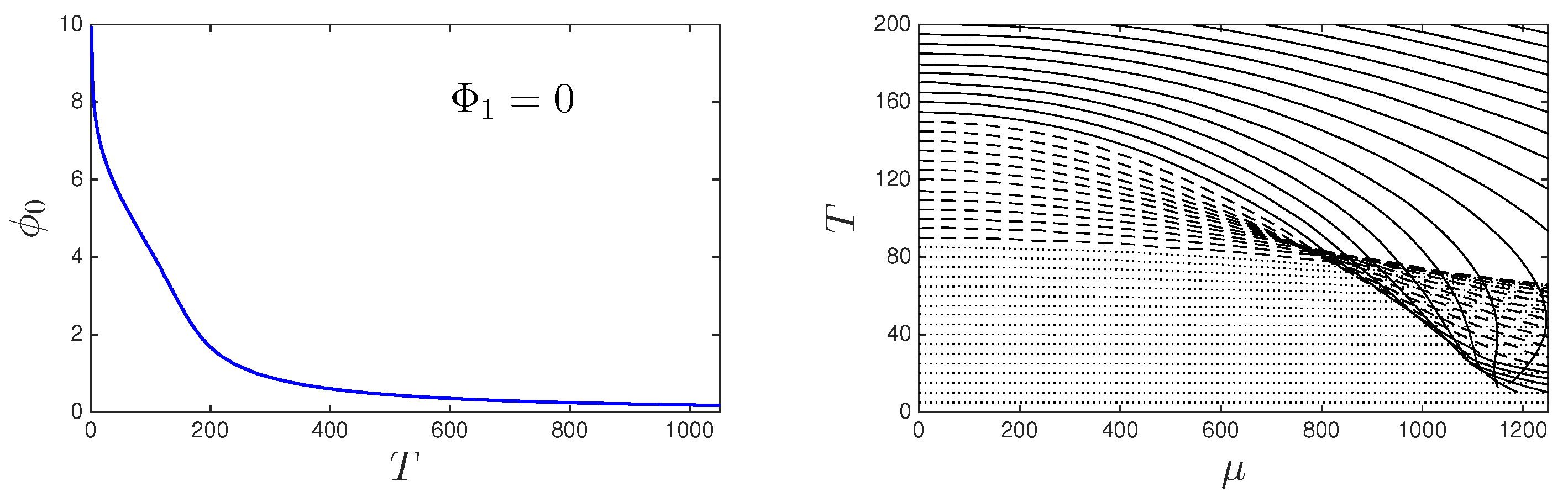
2. Black Hole Model
3. Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ratti, C. Lattice QCD and heavy ion collisions: A review of recent progress. Rept. Prog. Phys. 2018, 81, 084301. [Google Scholar] [CrossRef] [PubMed]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Mukherjee, S.; Ohno, H.; Petreczky, P.; et al. QCD equation of state to from lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Bellwied, R.; Borsanyi, S.; Fodor, Z.; Günther, J.; Katz, S.D.; Ratti, C.; Szabo, K.K. The QCD phase diagram from analytic continuation. Phys. Lett. B 2015, 751, 559–564. [Google Scholar] [CrossRef]
- Maldacena, J.M. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Gubser, S.S.; Nellore, A. Mimicking the QCD equation of state with a dual black hole. Phys. Rev. D 2008, 78, 086007. [Google Scholar] [CrossRef]
- DeWolfe, O.; Gubser, S.S.; Rosen, C. A holographic critical point. Phys. Rev. D 2011, 83, 086005. [Google Scholar] [CrossRef]
- DeWolfe, O.; Gubser, S.S.; Rosen, C. Dynamic critical phenomena at a holographic critical point. Phys. Rev. D 2011, 84, 126014. [Google Scholar] [CrossRef]
- Critelli, R.; Noronha, J.; Noronha-Hostler, J.; Portillo, I.; Ratti, C.; Rougemont, R. Critical point in the phase diagram of primordial quark-gluon matter from black hole physics. Phys. Rev. D 2017, 96, 096026. [Google Scholar] [CrossRef]
- Portillo, I. Baryon susceptibilities from a holographic equation of state. Nucl. Phys. A 2017, 967, 916–919. [Google Scholar] [CrossRef]
- Portillo, I. Susceptibilities from a black hole engineered EoS with a critical point. J. Phys. Conf. Ser. 2017, 832, 012041. [Google Scholar] [CrossRef]
- Rougemont, R.; Noronha, J.; Noronha-Hostler, J. Suppression of Baryon Diffusion and Transport in a Baryon Rich Strongly Coupled Quark-Gluon Plasma. Phys. Rev. Lett. 2015, 115, 202301. [Google Scholar] [CrossRef] [PubMed]
- Rougemont, R.; Ficnar, A.; Finazzo, S.; Noronha, J. Oscillons in a perturbed signum-Gordon model. J. High Energy Phys. 2016, 4, 102. [Google Scholar]
- Rougemont, R.; Critelli, R.; Noronha-Hostler, J.; Noronha, J.; Ratti, C. Dynamical versus equilibrium properties of the QCD phase transition: A holographic perspective. Phys. Rev. D 2017, 96, 014032. [Google Scholar] [CrossRef]
- Finazzo, S.I.; Rougemont, R.; Marrochio, H.; Noronha, J. Hydrodynamic transport coefficients for the non-conformal quark-gluon plasma from holography. J. High Energy Phys. 2015, 2, 51. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portillo, I. Locating the QCD Critical Point Using Holographic Black Holes. Proceedings 2019, 10, 40. https://doi.org/10.3390/proceedings2019010040
Portillo I. Locating the QCD Critical Point Using Holographic Black Holes. Proceedings. 2019; 10(1):40. https://doi.org/10.3390/proceedings2019010040
Chicago/Turabian StylePortillo, Israel. 2019. "Locating the QCD Critical Point Using Holographic Black Holes" Proceedings 10, no. 1: 40. https://doi.org/10.3390/proceedings2019010040
APA StylePortillo, I. (2019). Locating the QCD Critical Point Using Holographic Black Holes. Proceedings, 10(1), 40. https://doi.org/10.3390/proceedings2019010040




