Hydrodynamization Time Near a Critical Point From a Holographic Bjorken Flow †
Abstract
:1. Introduction
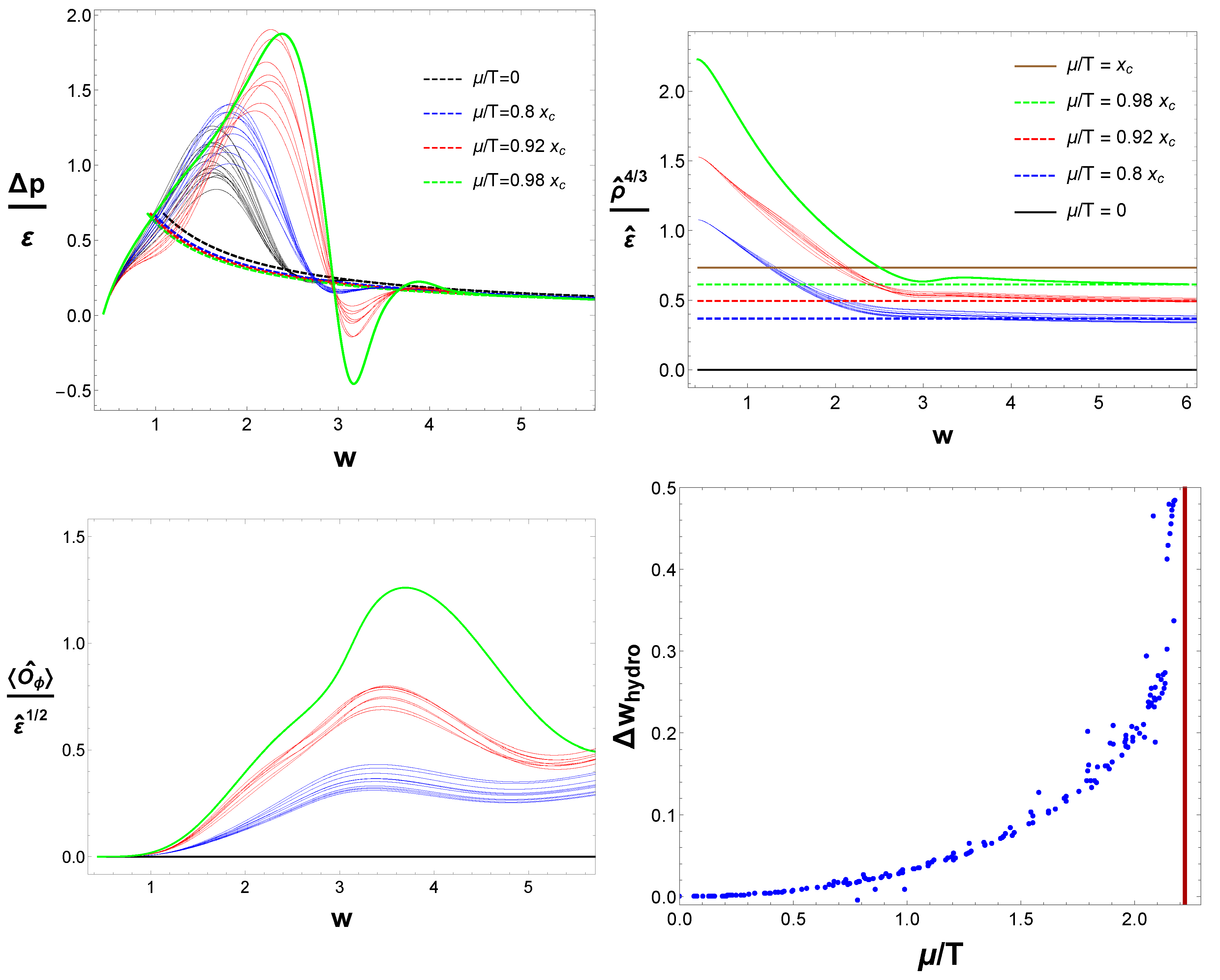
2. Results
3. Conclusions
Funding
Acknowledgments
References
- Gyulassy, M.; McLerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 2005, 750, 30. [Google Scholar] [CrossRef]
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2013, 63, 123. [Google Scholar] [CrossRef]
- Meyer, H.B. Transport Properties of the Quark-Gluon Plasma: A Lattice QCD Perspective. Eur. Phys. J. A 2011, 47, 86. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113. [Google Scholar] [CrossRef]
- Chesler, P.M.; Yaffe, L.G. Numerical solution of gravitational dynamics in asymptotically anti-de Sitter spacetimes. JHEP 2014, 1407, 086. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455. [Google Scholar] [CrossRef]
- Philipsen, O. The QCD equation of state from the lattice. Prog. Part. Nucl. Phys. 2013, 70, 55. [Google Scholar] [CrossRef]
- Bazavov, A. The QCD Equation of State to from Lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- DeWolfe, O.; Gubser, S.S.; Rosen, C. Dynamic critical phenomena at a holographic critical point. Phys. Rev. D 2011, 84, 126014. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef] [PubMed]
- Bjorken, J.D. Highly Relativistic Nucleus-Nucleus Collisions: The Central Rapidity Region. Phys. Rev. D 1983, 27, 140. [Google Scholar] [CrossRef]
- Chesler, P.M.; Yaffe, L.G. Boost invariant flow, black hole formation, and far-from-equilibrium dynamics in N = 4 supersymmetric Yang-Mills theory. Phys. Rev. D 2010, 82, 026006. [Google Scholar] [CrossRef]
- Heller, M.P.; Janik, R.A.; Witaszczyk, P. The characteristics of thermalization of boost-invariant plasma from holography. Phys. Rev. Lett. 2012, 108, 201602. [Google Scholar] [CrossRef] [PubMed]
- Critelli, R.; Rougemont, R.; Noronha, J. Holographic Bjorken flow of a hot and dense fluid in the vicinity of a critical point. Phys. Rev. D 2019, 99, 066004. [Google Scholar] [CrossRef]
- Gubser, S.S. Thermodynamics of spinning D3-branes. Nucl. Phys. B 1999, 551, 667. [Google Scholar] [CrossRef]
- Critelli, R.; Rougemont, R.; Noronha, J. Homogeneous isotropization and equilibration of a strongly coupled plasma with a critical point. JHEP 2017, 1712, 029. [Google Scholar] [CrossRef]
- Bluhm, M.; Jiang, Y.; Nahrgang, M.; Pawlowski, J.M.; Rennecke, F.; Wink, N. Time-evolution of fluctuations as signal of the phase transition dynamics in a QCD-assisted transport approach. Nucl. Phys. A 2019, 982, 871. [Google Scholar] [CrossRef]
- Critelli, R.; Noronha, J.; Noronha-Hostler, J.; Portillo, I.; Ratti, C.; Rougemont, R. Critical point in the phase diagram of primordial quark-gluon matter from black hole physics. Phys. Rev. D 2017, 96, 096026. [Google Scholar] [CrossRef]
- Gubser, S.S. Symmetry constraints on generalizations of Bjorken flow. Phys. Rev. D 2010, 82, 085027. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Critelli, R. Hydrodynamization Time Near a Critical Point From a Holographic Bjorken Flow. Proceedings 2019, 10, 48. https://doi.org/10.3390/proceedings2019010048
Critelli R. Hydrodynamization Time Near a Critical Point From a Holographic Bjorken Flow. Proceedings. 2019; 10(1):48. https://doi.org/10.3390/proceedings2019010048
Chicago/Turabian StyleCritelli, Renato. 2019. "Hydrodynamization Time Near a Critical Point From a Holographic Bjorken Flow" Proceedings 10, no. 1: 48. https://doi.org/10.3390/proceedings2019010048
APA StyleCritelli, R. (2019). Hydrodynamization Time Near a Critical Point From a Holographic Bjorken Flow. Proceedings, 10(1), 48. https://doi.org/10.3390/proceedings2019010048



