Reciprocal Quantum Channels †
Abstract
:1. Introduction
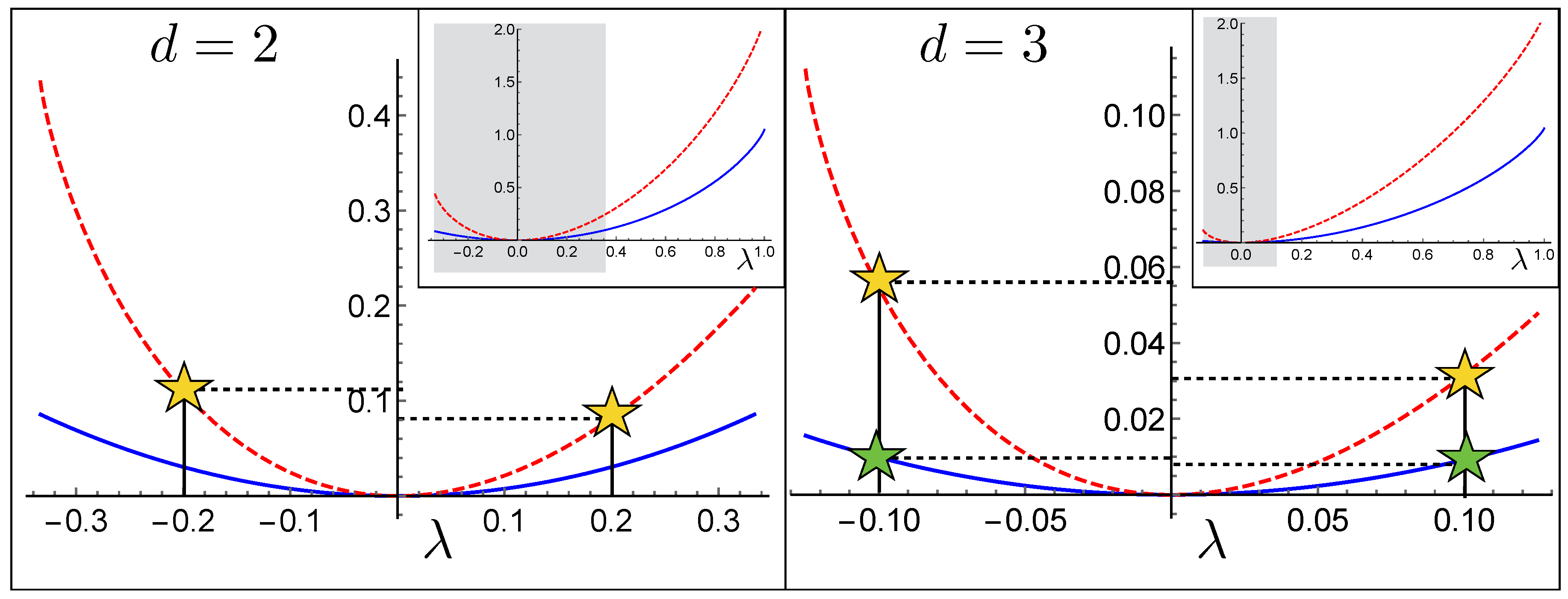
2. Results
References
- Gisin, N.; Popescu, S. Spin Flips and Quantum Information for Antiparallel Spins. Phys. Rev. Lett. 1999, 83, 432. [Google Scholar] [CrossRef]
- Rosati, M.; Giovannetti, V. Asymmetric information capacities of reciprocal pairs of quantum channels. Phys. Rev. A 2018, 97, 052318. [Google Scholar] [CrossRef]
- Holevo, A.S. Quantum Systems, Channels, Information: A Mathematical Introduction; De Gruyter Studies in Mathematical Physics; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- King, C. The capacity of the quantum depolarizing channel. IEEE Trans. Inf. Theory 2003, 49, 221. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giovannetti, V.; Rosati, M. Reciprocal Quantum Channels. Proceedings 2019, 12, 31. https://doi.org/10.3390/proceedings2019012031
Giovannetti V, Rosati M. Reciprocal Quantum Channels. Proceedings. 2019; 12(1):31. https://doi.org/10.3390/proceedings2019012031
Chicago/Turabian StyleGiovannetti, Vittorio, and Matteo Rosati. 2019. "Reciprocal Quantum Channels" Proceedings 12, no. 1: 31. https://doi.org/10.3390/proceedings2019012031
APA StyleGiovannetti, V., & Rosati, M. (2019). Reciprocal Quantum Channels. Proceedings, 12(1), 31. https://doi.org/10.3390/proceedings2019012031



