Manipulation of Cooper Pair Entanglement in Hybrid Topological Josephson Junctions †
Abstract
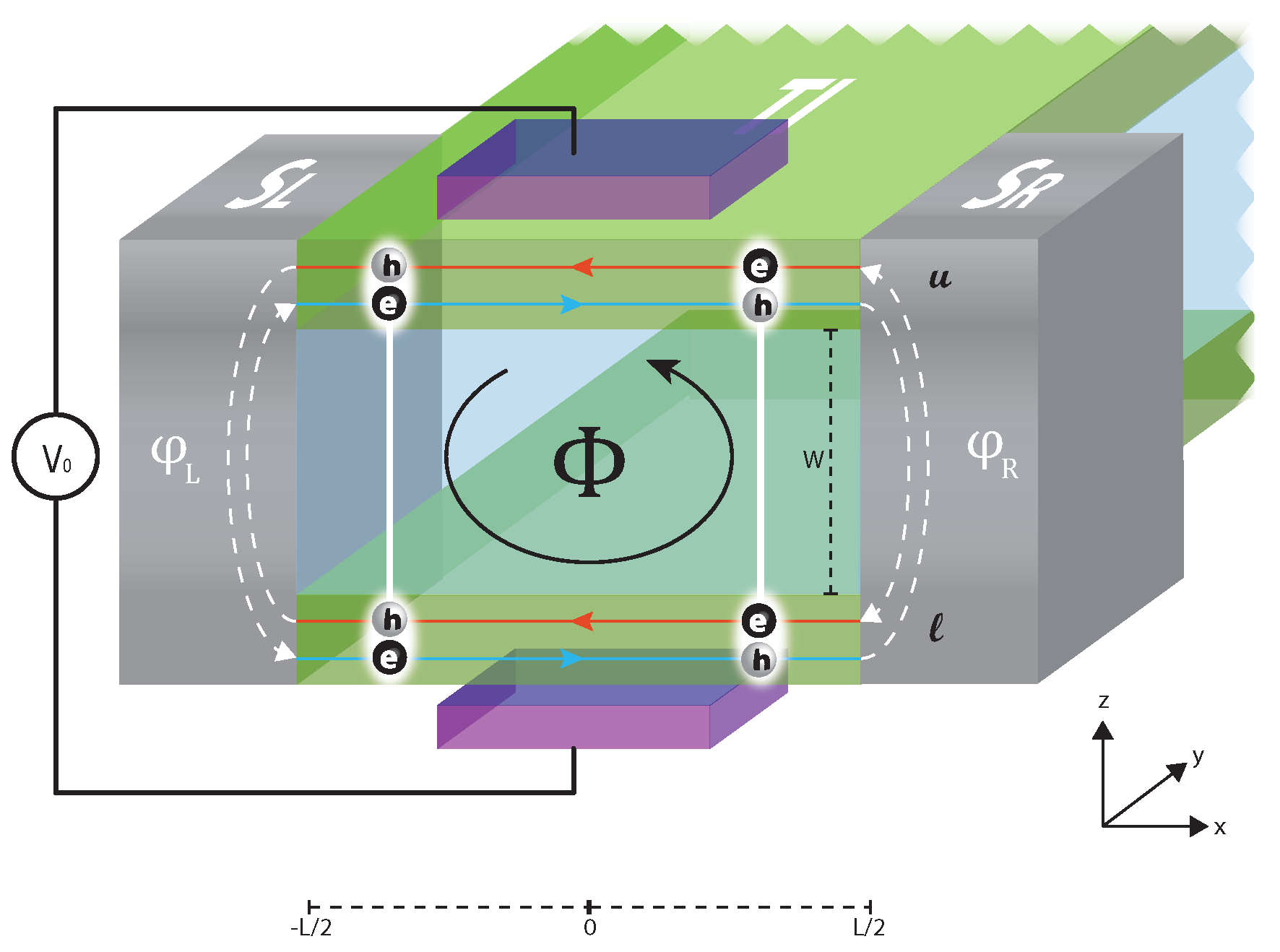
:1. The Setup
2. The Model
3. Local Fields Selective Action
4. Results
5. Conclusions
References
- Blasi, G.; Taddei, F.; Giovannetti, V.; Braggio, A. Manipulation of Cooper pair entanglement in hybrid topological Josephson junctions. arXiv 2018, arXiv:1808.09709. [Google Scholar]
- Xiao, X.; Liu, Y.; Liu, Z.; Ai, G.; Yang, S.A.; Zhou, G. All-electric spin modulator based on a two-dimensional topological insulator. Appl. Phys. Lett. 2016, 108, 032403. [Google Scholar] [CrossRef]
- Tkachov, G.; Burset, P.; Trauzettel, B.; Hankiewicz, E. Quantum interference of edge supercurrents in a two-dimensional topological insulator. Phys. Rev. B 2015, 92, 045408. [Google Scholar] [CrossRef]
- Sothmann, B.; Giazotto, F.; Hankiewicz, E.M. High-efficiency thermal switch based on topological Josephson junctions. New J. Phys. 2017, 19, 023056. [Google Scholar] [CrossRef]
- Büttiker, M. Four-Terminal Phase-Coherent Conductance. Phys. Rev. Lett. 1986, 57, 1761–1764. [Google Scholar] [CrossRef] [PubMed]
- Büttiker, M. Scattering theory of current and intensity noise correlations in conductors and wave guides. Phys. Rev. B 1992, 46, 12485–12507. [Google Scholar] [CrossRef] [PubMed]
- Lambert, C.J.; Raimondi, R. Phase-coherent transport in hybrid superconducting nanostructures. J. Phys. Condens. Matter 1998, 10, 901. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Universal limit of critical-current fluctuations in mesoscopic Josephson junctions. Phys. Rev. Lett. 1991, 67, 3836–3839. [Google Scholar] [CrossRef] [PubMed]
- Beenakker, C. Three “universal” mesoscopic Josephson effects. In Transport Phenomena in Mesoscopic Systems; Springer: Berlin/Heidelberg, Germany, 1992; pp. 235–253. [Google Scholar]
- Beenakker, C.W.J.; Emary, C.; Kindermann, M.; van Velsen, J.L. Proposal for Production and Detection of Entangled Electron-Hole Pairs in a Degenerate Electron Gas. Phys. Rev. Lett. 2003, 91, 147901. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blasi, G.; Taddei, F.; Giovannetti, V.; Braggio, A. Manipulation of Cooper Pair Entanglement in Hybrid Topological Josephson Junctions. Proceedings 2019, 12, 44. https://doi.org/10.3390/proceedings2019012044
Blasi G, Taddei F, Giovannetti V, Braggio A. Manipulation of Cooper Pair Entanglement in Hybrid Topological Josephson Junctions. Proceedings. 2019; 12(1):44. https://doi.org/10.3390/proceedings2019012044
Chicago/Turabian StyleBlasi, Gianmichele, Fabio Taddei, Vittorio Giovannetti, and Alessandro Braggio. 2019. "Manipulation of Cooper Pair Entanglement in Hybrid Topological Josephson Junctions" Proceedings 12, no. 1: 44. https://doi.org/10.3390/proceedings2019012044
APA StyleBlasi, G., Taddei, F., Giovannetti, V., & Braggio, A. (2019). Manipulation of Cooper Pair Entanglement in Hybrid Topological Josephson Junctions. Proceedings, 12(1), 44. https://doi.org/10.3390/proceedings2019012044




