Influence of Spatial and Dynamical Anisotropies on Flow and Femtoscopy Radii in Relativistic Heavy-Ion Collisions at LHC Energies †
Abstract
:1. Introduction
2. HYDJET++ Model
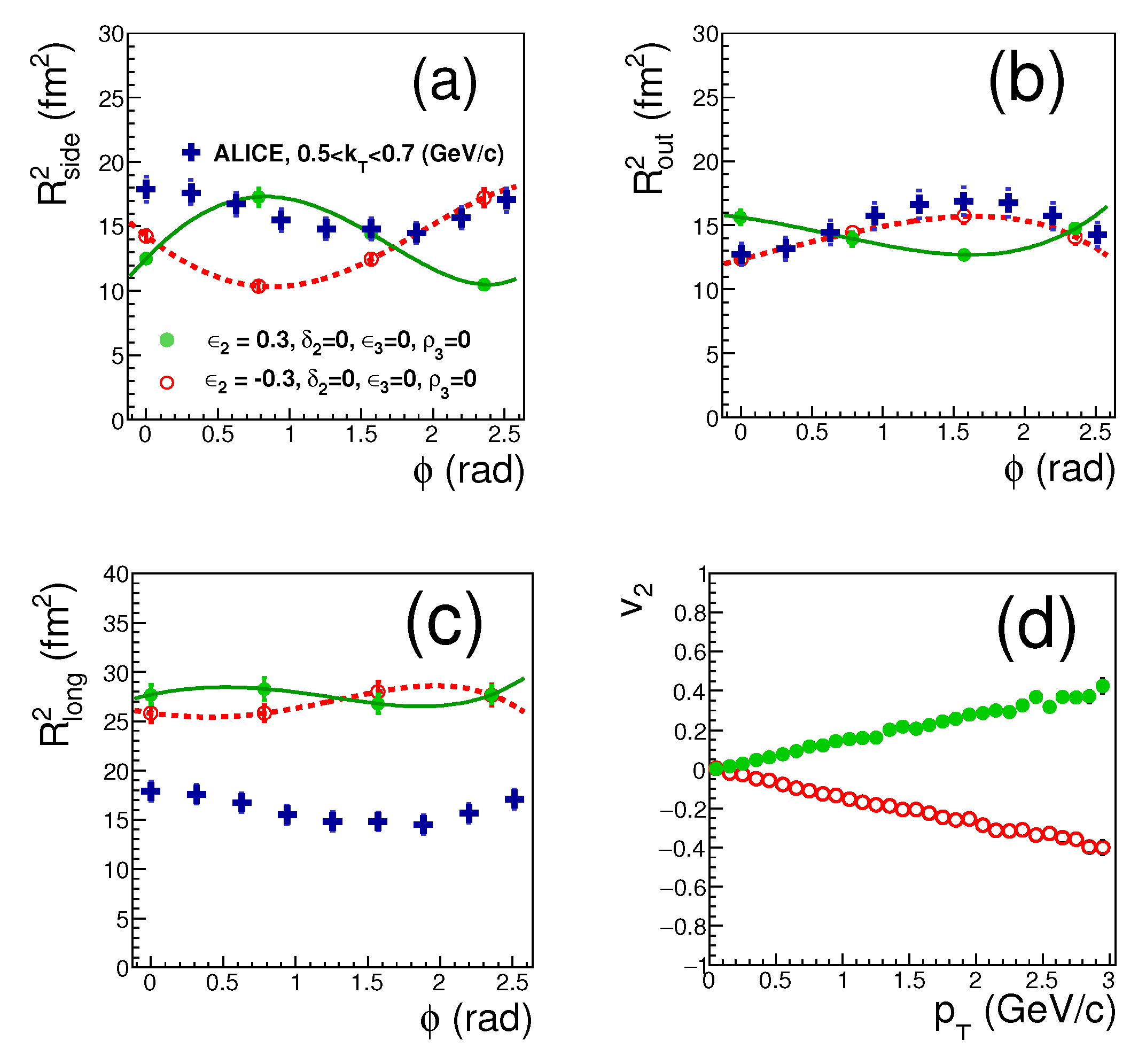
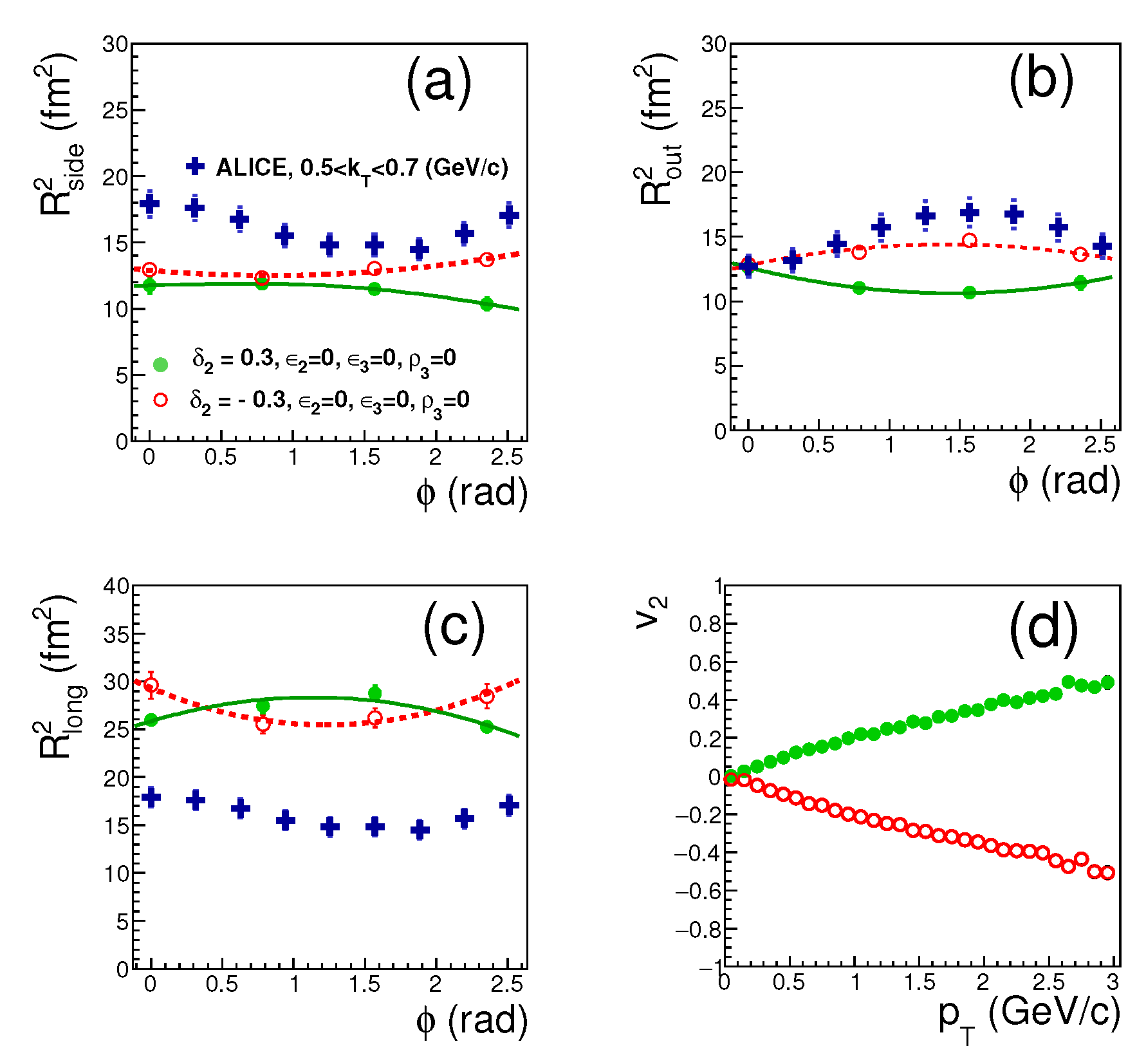
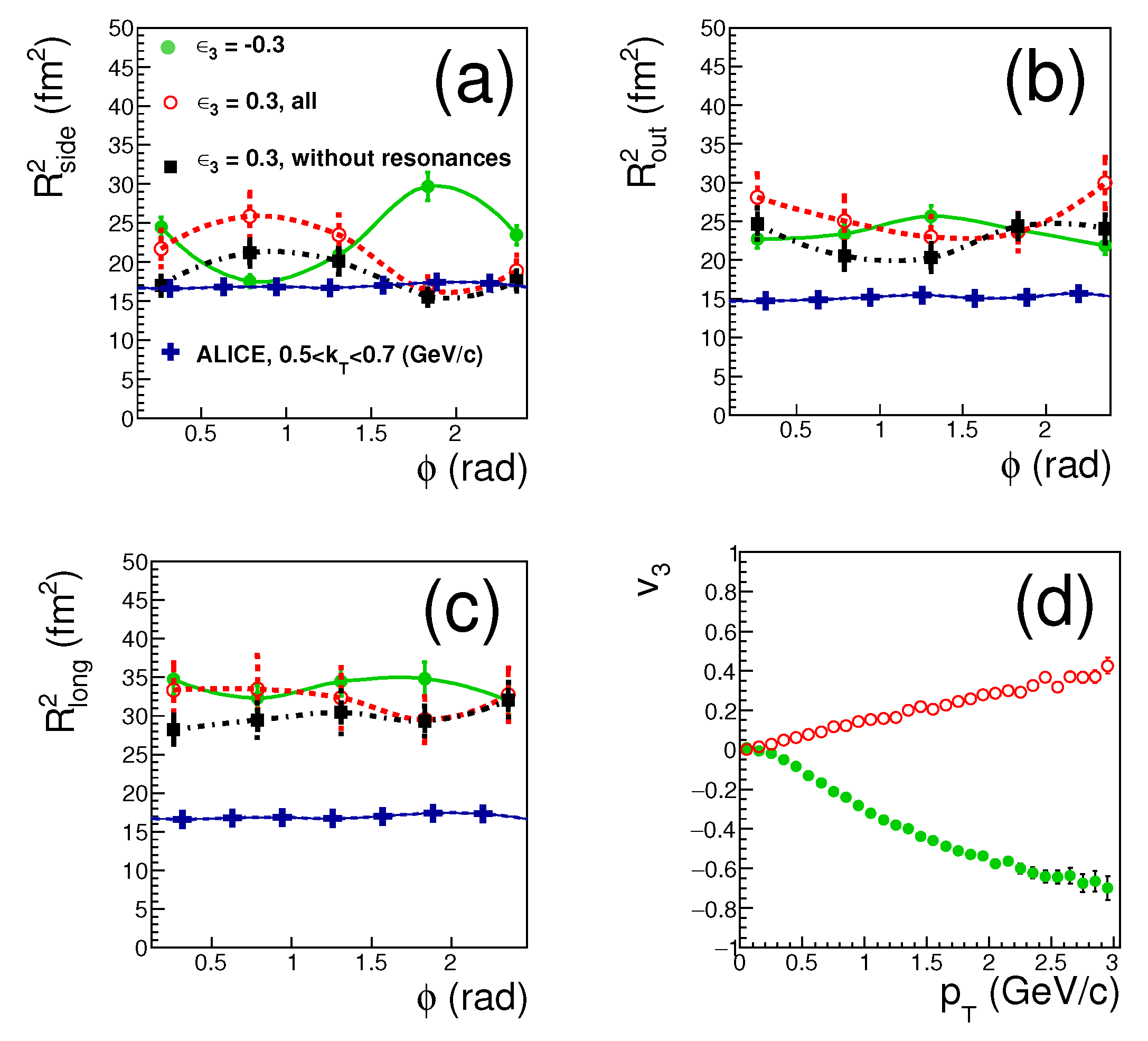
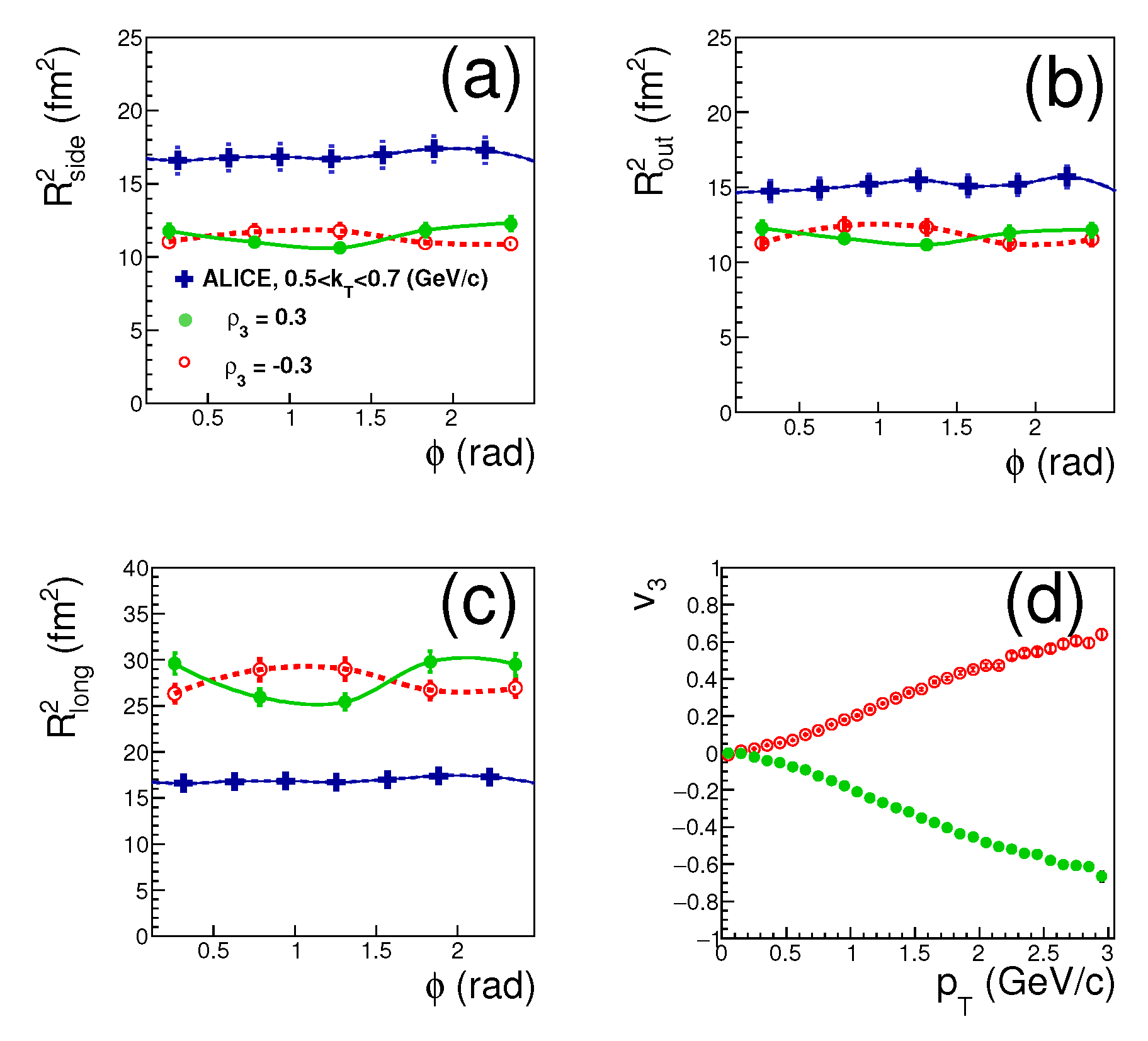
3. Results of the Simultaneous Description of , , and Oscillations of Femtoscopic Radii
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Voloshin, S.A.; Poskanzer, A.M.; Snellings, R. Collective phenomena in non-central nuclear collisions. Landolt-Börnstein 2010, 23, 293–333. [Google Scholar] [CrossRef]
- Qin, G.-Y.; Petersen, H.; Bass, S.A.; Muller, B. Translation of collision geometry fluctuations into momentum anisotropies in relativistic heavy-ion collisions. Phys. Rev. C 2010, 82, 064903. [Google Scholar] [CrossRef]
- Borghini, N.; Ollitrault, J.-Y. Momentum spectra, anisotropic flow, and ideal fluids. Phys. Lett. B 2006, 642, 49–54. [Google Scholar] [CrossRef]
- Bravina, L.V.; Brusheim Johansson, B.H.; Eyyubova, G.K.; Korotkikh, V.L.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M.; Zabrodin, E.E. Hexagonal flow v6 as a superposition of elliptic v2 and triangular v3 flows. Phys. Rev. C 2014, 89, 024909. [Google Scholar] [CrossRef]
- Amelin, N.S.; Lednicky, R.; Lokhtin, I.P.; Malinina, L.V.; Snigirev, A.M.; Karpenko, I.A.; Sinyukov, Y.M.; Arsene, I.; Bravina, L. Fast hadron freeze-out generator. Part II. Noncentral collisions. Phys. Rev. C 2008, 77, 014903. [Google Scholar] [CrossRef]
- Podgoretsky, M.I. Interference Correlations of Identical Pions: Theory (In Russian). Fiz. Elem. Chast. Atom. Yadra 1989, 20, 628–668. [Google Scholar]
- Lednicky, R. Correlation femtoscopy of multiparticle processes. Phys. Atom. Nucl. 2004, 67, 72–82. [Google Scholar] [CrossRef]
- Lisa, M.; Pratt, S.; Soltz, R.; Wiedemann, U. Femtoscopy in relativistic heavy ion collisions. Ann. Rev. Nucl. Part Sci. 2005, 55, 357–402. [Google Scholar] [CrossRef]
- Podgoretsky, M.I. On the Comparison of Identical Pion Correlations in Different Reference Frames. Sov. J. Nucl. Phys. 1983, 37, 272–278. [Google Scholar]
- Bertsch, G.F.; Danielewicz, P.; Herrmann, M. Hanbury-Brown-Twiss analysis in a solvable model. Phys. Rev. C 1994, 49, 442–451. [Google Scholar] [CrossRef] [PubMed]
- Chapman, S.; Scotto, P.; Heinz, U. A New cross term in the two particle HBT correlation function. Phys. Rev. Lett. 1995, 74, 4400–4403. [Google Scholar] [CrossRef] [PubMed]
- Niida, T. et al. [PHENIX Collaboration] Detailed HBT measurements with respect to the event plane and collision energy in Au+Au collisions at PHENIX. Nucl. Phys. A 2013, 904, 439c–442c. [Google Scholar] [CrossRef]
- Adamova, D.; et al. [ALICE Collaboration] Azimuthally Differential Pion Femtoscopy in Pb-Pb Collisions at sNN=2.76 TeV. Phys. Rev. Lett. 2017, 118, 222301. [Google Scholar] [CrossRef]
- Acharya, S.; et al. [ALICE Collaboration] Azimuthally-differential pion femtoscopy relative to the third harmonic event plane in Pb-Pb collisions at sNN=2.76 TeV. Phys. Lett. B 2018, 785, 320–331. [Google Scholar] [CrossRef]
- Heinz, U.; Kolb, P.F. Emission angle dependent pion interferometry at RHIC and beyond. Phys. Lett. B 2002, 542, 216–222. [Google Scholar] [CrossRef]
- Plumberg, C.J.; Shen, C.; Heinz, U. Hanbury-Brown–Twiss interferometry relative to the triangular flow plane in heavy-ion collisions. Phys. Rev. C 2013, 88, 044914. [Google Scholar] [CrossRef]
- Lökös, S.; Csanad, M.; Tomasik, B.; Csorgo, T. Higher order anisotropies in the Buda-Lund model: Disentangling flow and density field anisotropies. Eur. Phys. J. A 2016, 52, 311. [Google Scholar] [CrossRef]
- Cimerman, J.; Tomasik, B.; Csanad, M.; Lökös, S. Higher-order anisotropies in the Blast-Wave Model– Disentangling flow and density field anisotropies. Eur. Phys. J. A 2017, 53, 161. [Google Scholar] [CrossRef]
- Bravina, L.V.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M.; Zabrodin, E.E. Dynamical vs. geometric anisotropy in relativistic heavy-ion collisions. Which one prevails? Eur. Phys. J. A 2017, 53, 219. [Google Scholar] [CrossRef]
- Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M.; Arsene, I.; Tywoniuk, K. Heavy ion event generator HYDJET++ (HYDrodynamics plus JETs). Comput. Phys. Commun. 2009, 180, 779–799. [Google Scholar] [CrossRef]
- Amelin, N.S.; Lednicky, R.; Pocheptsov, T.A.; Lokhtin, I.P.; Malinina, L.V.; Snigirev, A.M.; Karpenko, I.A.; Sinyukov, Y.M. A fast hadron freeze-out generator. Phys. Rev. C 2006, 74, 064901. [Google Scholar] [CrossRef]
- Lokhtin, I.P.; Snigirev, A.M. A Model of jet quenching in ultrarelativistic heavy ion collisions and high-p(T) hadron spectra at RHIC. Eur. Phys. J. C 2005, 45, 211–217. [Google Scholar] [CrossRef]
- Braaten, E.; Thoma, M. Energy loss of a heavy fermion in a hot plasma. Phys. Rev. D 1991, 44, 1298–1310. [Google Scholar] [CrossRef]
- Lokhtin, I.P.; Snigirev, A.M. Nuclear geometry of jet quenching. Eur. Phys. J. C 2000, 16, 527–536. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Peigne, S.; Schiff, D. Radiative energy loss of high-energy quarks and gluons in a finite volume quark-gluon plasma. Nucl. Phys. B 1997, 483, 291–320. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Schiff, D. Angular dependence of the radiative gluon spectrum and the energy loss of hard jets in QCD media. Phys. Rev. C 1999, 60, 064902. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Schiff, D. On the angular dependence of the radiative gluon spectrum. Phys. Rev. C 2001, 64, 057902. [Google Scholar] [CrossRef]
- Tywoniuk, K.; Arsene, I.C.; Bravina, L.; Kaidalov, A.B.; Zabrodin, E. Gluon shadowing in the Glauber-Gribov model at HERA. Phys. Lett. B 2007, 657, 170–175. [Google Scholar] [CrossRef]
- Bravina, L.V.; Fotina, E.S.; Korotkikh, V.L.; Lokhtin, I.P.; Malinina, L.V.; Nazarova, E.N.; Petrushanko, S.V.; Snigirev, A.M.; Zabrodin, E.E. Anisotropic flow fluctuations in hydro-inspired freeze-out model for relativistic heavy ion collisions. Eur. Phys. J. C 2015, 75, 588. [Google Scholar] [CrossRef]
- Eyyubova, G.; Bravina, L.; Korotkih, V.L.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M.; Zabrodin, E. Jets and decays of resonances: Two mechanisms responsible for reduction of elliptic flow at the CERN Large Hadron Collider (LHC) and restoration of constituent quark scaling. Phys. Rev. C 2009, 80, 064907. [Google Scholar] [CrossRef]
- Zabrodin, E.E.; Bravina, L.V.; Eyyubova, G.K.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M. Influence of jets and resonance decays on the constituent quark scaling of elliptic flow. J. Phys. G 2010, 37, 094060. [Google Scholar] [CrossRef]
- Crkovská, J.; Bielčík, J.; Bravina, L.; Johansson, B.H.B.; Zabrodin, E.; Eyyubova, G.; Korotkikh, V.L.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; et al. Influence Jets Decays Reson. Triangular Flow Ultrarelativistic Heavy-Ion Collisions. Phys. Rev. C 2017, 95, 014910. [Google Scholar] [CrossRef]
- Zabrodin, E.E.; Bravina, L.V.; Brusheim Johansson, B.H.; Crkovská, J.; Eyyubova, G.K.; Korotkikh, V.L.; Malinina, L.V.; Petrushanko, S.S.; Snigirev, A.M. Snigirev, A.M. Features of triangular flow of strange and non-strange hadrons at LHC. J. Phys. Conf. Ser. 2016, 668, 012099. [Google Scholar] [CrossRef]
- Bravina, L.V.; Brusheim Johansson, B.H.; Eyyubova, G.K.; Korotkikh, V.L.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M.; Zabrodin, E.E. Higher harmonics of azimuthal anisotropy in relativistic heavy ion collisions in HYDJET++ model. Eur. Phys. J. C 2014, 74, 2807. [Google Scholar] [CrossRef]
- Bravina, L.; Brusheim Johansson, B.H.; Eyyubova, G.; Zabrodin, E. Effect of jets on the v4/v22 ratio, and constituent quark scaling in relativistic heavy-ion collisions. Phys. Rev. C 2013, 87, 034901. [Google Scholar] [CrossRef]
- Eyyubova, G.K.; Korotkikh, V.L.; Lokhtin, I.P.; Petrushanko, S.V.; Snigirev, A.M.; Bravina, L.V.; Zabrodin, E.E. Angular dihadron correlations as an interplay between elliptic and triangular flows. Phys. Rev. C 2015, 91, 064907. [Google Scholar] [CrossRef]
- Lokhtin, I.P.; Belyaev, A.V.; Ponimatkin, G.; Pronina, E.Y.; Eyyubova, G.K. On the possibility of thermalization of heavy mesons in ultrarelativistic nuclear collisions. J. Exp. Theor. Phys. 2017, 124, 244–250. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabrodin, E.E.; Bravina, L.V.; Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M. Influence of Spatial and Dynamical Anisotropies on Flow and Femtoscopy Radii in Relativistic Heavy-Ion Collisions at LHC Energies. Proceedings 2019, 13, 3. https://doi.org/10.3390/proceedings2019013003
Zabrodin EE, Bravina LV, Lokhtin IP, Malinina LV, Petrushanko SV, Snigirev AM. Influence of Spatial and Dynamical Anisotropies on Flow and Femtoscopy Radii in Relativistic Heavy-Ion Collisions at LHC Energies. Proceedings. 2019; 13(1):3. https://doi.org/10.3390/proceedings2019013003
Chicago/Turabian StyleZabrodin, E. E., L. V. Bravina, I. P. Lokhtin, L. V. Malinina, S. V. Petrushanko, and A. M. Snigirev. 2019. "Influence of Spatial and Dynamical Anisotropies on Flow and Femtoscopy Radii in Relativistic Heavy-Ion Collisions at LHC Energies" Proceedings 13, no. 1: 3. https://doi.org/10.3390/proceedings2019013003
APA StyleZabrodin, E. E., Bravina, L. V., Lokhtin, I. P., Malinina, L. V., Petrushanko, S. V., & Snigirev, A. M. (2019). Influence of Spatial and Dynamical Anisotropies on Flow and Femtoscopy Radii in Relativistic Heavy-Ion Collisions at LHC Energies. Proceedings, 13(1), 3. https://doi.org/10.3390/proceedings2019013003




