Principal Components Analysis (PCA) of Monument Stone Decay by Rainwater: A Case Study of “Basílica da Estrela” Church, Portugal †
Abstract
:1. Introduction
2. Methods
2.1. Data Sampling
2.2. Principal Components Analysis (PCA)
2.2.1. The Rational
2.2.2. General Methodological Algorithm: A Simple Layout
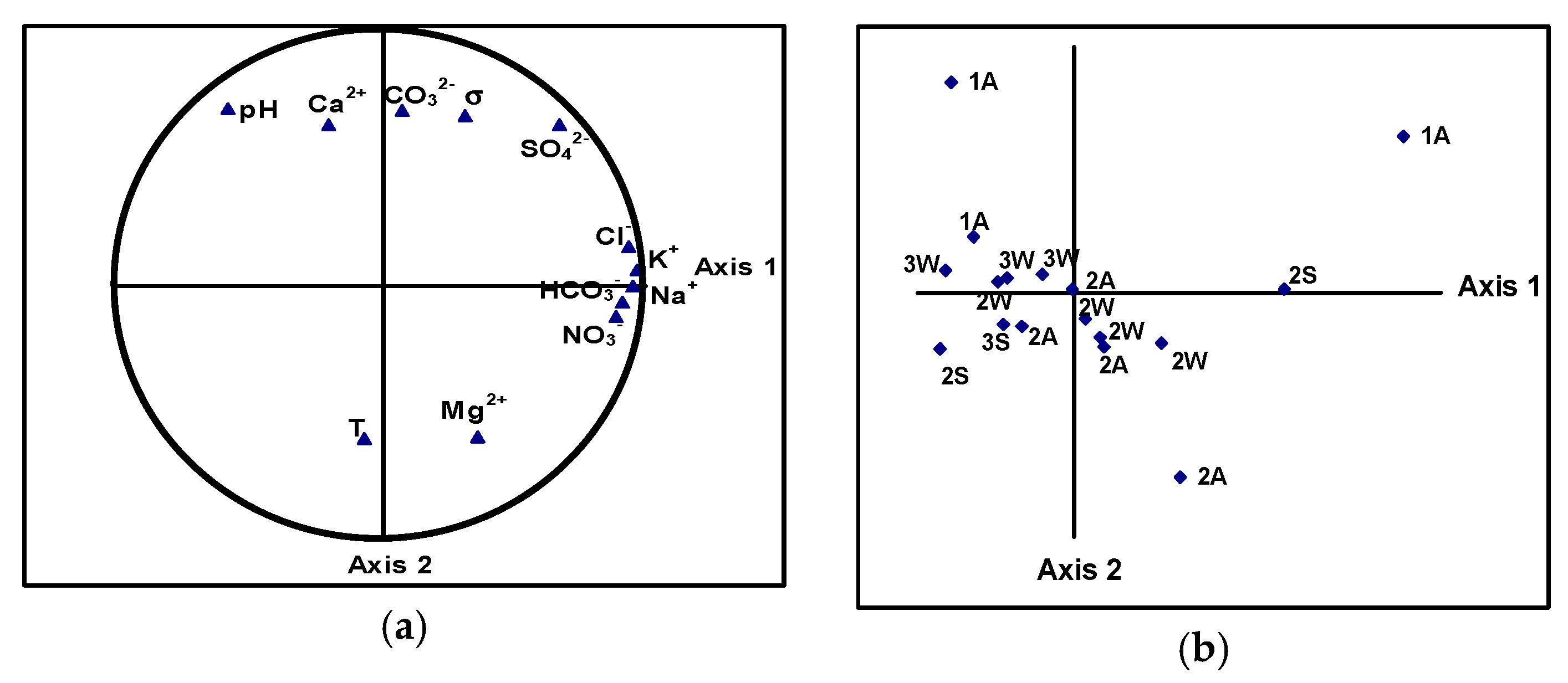
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Figueiredo, C.A.M.; Marques, J.M.; Maurício, A.M.; Aires-Barros, L. Water-rock Interaction and Monuments Stone Decay: The case of Basílica da Estrela, Portugal. In Proceedings of the 9th International Congresso on Deterioration and Conservation of Stone, Venice, Italy, 19–24 June 2000; Fassina, V., Ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2000; Volume 1, pp. 79–87. [Google Scholar]
- Figueiredo, C.A.M.; Maurício, A.M.; Aires-Barros, L. A. Basílica da Estrela Stone Decay: The role of rain-water. In Proceedings of the 10th International Symposium on Water-Rock Interaction (WRI-10), Villasimius, Italy, 10–15 July 2001; Swets, R.C., Zeitlinger, A.A., Eds.; Balkema Publishers: Lisse, The Netherlands, 2001; Volume 1, pp. 387–390, ISBN 90-2651-824-2. [Google Scholar]
- Figueiredo, C.A.M.; Aires-Barros, L.; Basto, M.J.; Graça, R.C.; Maurício, A.M. The Weathering and Weatherability of Basílica da Estrela Stones, Lisbon, Portugal. In Building Stone Decay: From Diagnosis to Conservation; Přikryl, R., Smith, B.J., Eds.; Special Publications; Geological Society: London, UK, 2007; Volume 271, pp. 99–107. [Google Scholar]
- Davis, J.C. Statistics and Data Analysis in Geology, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1986; p. 646. ISBN 0-471-83743-1. [Google Scholar]
- Moropoulou, A.; Polikreti, K. Principal Component Analysis in monument conservation: Three application examples. J. Cult. Heritage 2009, 10, 73–81. [Google Scholar] [CrossRef]
- Bacci, M.; Porcinai, S.; Radicati, B. Principal Component Analysis of Near-Infrared Spectra of Alteration Products in Calcareous Samples. Appl. Spectrosc. 1997, 51, 700–706. [Google Scholar] [CrossRef]
- Benavente, D.; Martínez-Martínez, J.; Cueto, N.; García-del-Cura, M.A. Salt weathering in dual-porosity building dolostones. Eng. Geol. 2007, 94, 215–226. [Google Scholar] [CrossRef]
- Maurício, A.M.; Aires-Barros, L.; Fassina, V.; Cassar, J.; Torpiano, A. Multivariate Data Analysis Applied to Salt Efflorescences Occuring at Sta. Marija Tà Cwerra Church (Malta). In Proceedings of the European Commission Research Workshop on Origin, Mechanisms and Effects of Salts on Degradation of Monuments in Marine and Continental Environments, Protection and Conservation of the European Cultural Heritage, Research Report nº 4, Bari, Italy, 25–27 March 1996; Zezza, F., Ed.; pp. 395–402. [Google Scholar]
- Torfs, K.; Van Grieken, R.; Cassar, J. Environmental effects on deterioration of monuments: case study of the Church of Sta. Marija Tà Cwerra, Malta. Environmental effects on deterioration of monuments: case study of the Church of Sta. Marija Tà Cwerra, Malta. In Proceedings of the European Commission Research Workshop on Origin, Mechanisms and Effects of Salts on Degradation of Monuments in Marine and Continental Environments, Protection and Conservation of the European Cultural Heritage, Research Report nº 4, Bari, Italy, 25–27 March 1996; Zezza, F., Ed.; pp. 443–451. [Google Scholar]
- Zezza, F.; Torfs, K.; Van Grieken, R.; García Pascua, N.; Macrì, F. Study of environmental effects on deterioration of monuments: case study of the Cathedral of Bari, Italy. In Proceedings of the European Commission Research Workshop on Origin, Mechanisms and Effects of Salts on Degradation of Monuments in Marine and Continental Environments, Protection and Conservation of the European Cultural Heritage, Research Report nº 4, Bari, Italy, 25–27 March 1996; Zezza, F., Ed.; pp. 461–471. [Google Scholar]
| Variables—Physical and Chemical Properties | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | pH | σ (µS/cm) | HCO3− (%) | CO32− (%) | Cl− (%) | NO3− (%) | SO42− (%) | Na+ (%) | K+ (%) | Ca2+ (%) | Mg2+ (%) | |
| MAX | 25.0 | 11.7 | 1424.0 | 310.6 | 163.7 | 67.4 | 20.5 | 29.9 | 122.5 | 330.0 | 46.5 | 0.20 |
| AV | 19.5 | 10.3 | 722.4 | 111.0 | 98.5 | 34.9 | 9.4 | 9.1 | 67.6 | 177.9 | 4.4 | 0.06 |
| MIN | 16.7 | 8.2 | 100.4 | 4.0 | 1.2 | 23.7 | 0.00 | 0.00 | 41.0 | 115.0 | 0.7 | 0.00 |
| STD | 2.3 | 0.8 | 305.9 | 93.2 | 36.1 | 11.8 | 6.0 | 7.1 | 22.5 | 58.2 | 10.9 | 0.06 |
| T | pH | σ | HCO3− | CO32− | Cl− | NO3− | SO42− | Na+ | K+ | Ca2+ | Mg2+ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | 1.00 | |||||||||||
| pH | −0.35 | 1.00 | ||||||||||
| σ | −0.23 | 0.20 | 1.00 | |||||||||
| HCO3− | −0.08 | −0.62 | 0.07 | 1.00 | ||||||||
| CO32− | −0.26 | 0.58 | 0.24 | 0.05 | 1.00 | |||||||
| Cl− | −0.15 | −0.40 | 0.32 | 0.90 | 0.22 | 1.00 | ||||||
| NO3− | 0.16 | −0.55 | 0.29 | 0.72 | 0.04 | 0.78 | 1.00 | |||||
| SO42− | −0.39 | −0.01 | 0.65 | 0.56 | 0.41 | 0.67 | 0.48 | 1.00 | ||||
| Na+ | −0.14 | −0.54 | 0.27 | 0.87 | 0.05 | 0.86 | 0.81 | 0.63 | 1.00 | |||
| K+ | −0.10 | −0.49 | 0.31 | 0.86 | 0.18 | 0.94 | 0.86 | 0.66 | 0.90 | 1.00 | ||
| Ca2+ | −0.28 | 0.45 | 0.58 | −0.25 | 0.07 | −0.19 | −0.22 | 0.28 | −0.13 | −0.23 | 1.00 | |
| Mg2+ | 0.22 | −0.56 | −0.09 | 0.190 | −0.47 | 0.12 | 0.42 | −0.12 | 0.46 | 0.30 | −0.24 | 1.00 |
| Eigenvectors | I | II | III | IV | V | |||||||
| Eigenvalues | 5.422 | 2.960 | 1.284 | 0.837 | 0.599 | |||||||
| Percentage of total variance contributed by each eigenvalue | ||||||||||||
| 45.2% | 24.7% | 10.7% | 7.0% | 5.0% | ||||||||
| Cumulative (%) value of total variance | ||||||||||||
| 45.2% | 69.90% | 80.60% | 87.60% | 92.60% | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figueiredo, C.; Alves, C. Principal Components Analysis (PCA) of Monument Stone Decay by Rainwater: A Case Study of “Basílica da Estrela” Church, Portugal. Proceedings 2018, 2, 560. https://doi.org/10.3390/IECG_2018-05339
Figueiredo C, Alves C. Principal Components Analysis (PCA) of Monument Stone Decay by Rainwater: A Case Study of “Basílica da Estrela” Church, Portugal. Proceedings. 2018; 2(10):560. https://doi.org/10.3390/IECG_2018-05339
Chicago/Turabian StyleFigueiredo, Carlos, and Carlos Alves. 2018. "Principal Components Analysis (PCA) of Monument Stone Decay by Rainwater: A Case Study of “Basílica da Estrela” Church, Portugal" Proceedings 2, no. 10: 560. https://doi.org/10.3390/IECG_2018-05339
APA StyleFigueiredo, C., & Alves, C. (2018). Principal Components Analysis (PCA) of Monument Stone Decay by Rainwater: A Case Study of “Basílica da Estrela” Church, Portugal. Proceedings, 2(10), 560. https://doi.org/10.3390/IECG_2018-05339






