A Derivative Free Non-Linear Programming Method for the Optimal Setting of PATs to Be Used in a Hybrid Genetic Algorithm: A Preliminary Work ^†

Abstract

In recent years, recovering energy while managing excessive pressure in water distribution networks (WDNs) has gradually taken hold through the use of Pumps as Turbines (PATs). Therefore, algorithms commonly used for the optimizations of WDNs require modifications to incorporate these devices. Within this study, an intermediate step toward a new Hybrid Genetic Algorithm (HGA) for the optimal placement and setting of PATs within WDNs is proposed. The described methodology is based on a non-linear optimization algorithm, the Powell Direction Set (PDS) method. For each WDN configuration with PATs, a non-linear univariate function, namely the energy production subjected to pressure and technical constraints, is maximized by the PDS method. The promising capabilities of the algorithm are demonstrated with a case study.

1. Introduction

Water Distribution Networks (WDNs) are commonly considered low efficiency systems due to the high energy required to deliver water to users. In many countries, they represent one of the main cause of energy consumption. In the UK it is estimated to be the fourth most consuming activity [1], while in the US operation and maintenance costs are of about 4 billion dollars per year [2]. A large amount of energy is lost through pumping systems because of water leakages occurring within WDNs. Leakages may cause inefficient energy distribution through the network, wasting energy otherwise available for pumping water, and they may also affect water quality by allowing the introduction of pathogens during low pressure conditions. As a consequence, leakages reduction techniques have attracted the interest of many researchers and practitioners. In the literature, several works have been devoted to leakage reduction through Pressure Management (PM) techniques based on the optimal location of pressure reducing devices [3,4], such as Pressure Reducing Valves (PRV). The use of these devices revealed to be effective, however, in this way, the excess of energy through the WDN is inevitably wasted.

In recent years, the concept of generating energy by exploiting the pressure excesses within WDNs has gradually taken hold. To reduce the excess of pressure and, at the same time, transform the dissipated energy into readily available electric energy, several researches have recently focused their attention on the use of turbines or pumps working as turbines (PATs) as an alternative to PRVs. In particular, PATs have become very attractive because of their lower costs and large scale production.

As shown in [5], few investigations have faced the problem of the optimal location of hydropower devices within WDNs. Indeed, the optimal placement of PATs within WDNs is a complex problem. Its complexity is strictly related to the WDN configuration. Moreover, placing a PAT within a pipe of a WDN characterized by several loops imply the insurgence of a concentrated head loss that can significantly influence the flow rate distribution as well as the available power. In addition, the governing equations of water motion are non-linear, and the number of decision variables involved in the optimization problem can be very large depending on the WDN size.

The afore mentioned problem is usually tackled by means of optimization techniques. In [6], to optimize either pressure reduction or power output potential, a Genetic Algorithm (GA) was used to find the optimal location of a fixed number of turbines, with two different objective functions. in [7], a mixed-integer optimization algorithm was used to perform a two-step optimization: in the first step, under steady average conditions, the optimal location of a fixed number of turbines was found by maximizing the power production, while, in the second step, the turbines were regulated according to the daily demand. Moreover, the governing equations were written as equality constraints of the optimization problem. However, in both [6,7], turbines were simulated as simple head losses. Conversely, in [8], affinity equations were used to simulate the behavior of real turbines within the WDN. The simulated annealing algorithm was used to return the best location of a fixed number of turbines, and the energy production was optimized for a real water network in Lausanne (Switzerland) [8]. In [8] the turbine size in each branch was assigned, while the presence of the turbine was a result of the optimization procedure. The produced power was then computed with reference to the yearly variability of the monthly-averaged daily pattern. In [5], to maximize the power output and reduce leakages, a mixed-integer non-linear programming algorithm was employed to find optimal location, setting, and number of PATs to be installed within a WDN. However, in this last work, the PATs were modeled as a concentrated head loss, and no affinity laws were employed.

The main concept of the present work lies on the following assumption: the optimal setting of a PAT within a WDN can be treated as Deterministic Polynomial Time Problem (P), while the problem of positioning, directing, and selecting the PAT can be treated as a Deterministic Non-Polynomial Hard Problem (NP-Hard). Based on this assumption, a Hybrid GA can be developed. In particular, the GA is assigned the task of finding the best number, position, direction, and type of PAT, while an inner non-linear programming algorithm is demanded to determine the electric regulated PAT optimal setting, in terms of rotational speed.

Therefore, we propose a new method for the optimal setting of variable speed PATs for assigned number, position, direction, and type. This goal is accomplished by means of a derivative free non-linear programming method, the Powell Direction Set (PDS) algorithm [9]. Epanet 2.0 DLLs [10] are used as external solver.

2. Methods

In this section, the optimization method and the objective function are described. The optimization algorithm, based on the PDS method, has several advantages over the classical non-linear programming algorithms: (i) it is derivative free, therefore continuity of the function and of its first derivative is not required; (ii) it does not require the function to be convex as it only requires the objective function to be univariate (i.e., the function must fulfill the condition of having just one maximum or minimum); (iii) it has quadratic convergence; (iv) constraints can be treated as penalty functions; (v) it is not too sensitive to noisy functions (i.e., it is able to find the optimal point even though the function may exhibit several small local spikes).

2.1. The External Hydraulic Solver

Hydraulic simulations were performed using an Extended Period Simulation (EPS) approach. To solve the WDN at the k-th time interval of the day, EPANET 2.0 DLLs [10] were used within the code. In particular PATs were modeled using the General Purpose Valve (GPV) option, thus defining the head loss curve into the input file for each setting of the electric regulated PAT, represented by relative speed V_j, namely the ratio between the setting speed N_j (in rpm) and the characteristic speed N_c,j of the j-th PAT.

2.2. The Powell Direction Set method

The PDS works on the basic principle that to find a minimum/maximum of a n-dimensional function, n-one dimensional minimizations can be executed along n directions [9]. The recursive algorithm works as follows:

• initialize a set of directions $u_i=e_i$ (where $e_i$ is the unitary vector basis of the n dimensional space) and select a starting point $P_0$;
• for $i=1\dots n$ move $P_{i-1}$ to a minimum along the direction $u_i$ and set $P_i=P_{i-1}$;
• for $i=1\dots \left(n-1\right)$ set $u_i=u_{i+1}$;
• set $u_n=P_n-P_0$;
• move $P_n$ to the minimum along the $u_n$ direction then set $P_0$ equal to this new point;
• repeat from step 2 until the convergence criterion is satisfied.

The above described procedure tends to create direction that are linearly dependent. To avoid this, the technique of discarding the direction of largest decrease [11] was employed here.

The line minimization technique employed are the Golden Section Search Method [12] (used to find the interval where the minimum lies) and the Brent method [9] to find the minimum of the function.

2.3. The Objective Function

To use the algorithm described in Section 2.2, a univariate objective function is required. Even though the PSD method does not account for the presence of constraints, this can be easily overcome by adding to the objective function a penalty function accounting for the presence of unfeasible regions. In this work, we propose the following objective function:

$$f_o(V)={\displaystyle \sum _{k=1}^{N_k}\left[P_k\left(V\right)-f_{p,k}\left(V\right)\right]}$$

(1)

where $V$ is the vector (with dimension equal to the number of PATs) of the PAT relative speed (ratio between the speed and the characteristic speed); N_k is the number of time intervals in which the day has been divided; $P_k\left(V\right)$ is the power produced by the PATs during the k-th time interval; $f_{p,k}\left(V\right)$ is the penalty function value at the k-th time interval.

2.3.1. Power Estimation

The power produced during the k-th time interval is equal to

$$P_k\left(V\right)={\displaystyle \sum _{j=1}^{N_{PAT}}\eta \left(V_j\right)Q\left(V_j\right)\mathsf{\Delta }H\left(V_j\right)}$$

(2)

where V_j is the relative speed of the j-th PAT; $\eta \left(V_j\right)$ is the efficiency of the j-th PAT; $Q\left(V_j\right)$ is the discharge flowing through the j-th PAT; $\mathsf{\Delta }H\left(V_j\right)$ is the head loss a-th the j-th PAT.

In particular, the head loss curve is estimated at the characteristic speed with the method proposed in [13].

$$\frac{{\eta }_c\left(Q_c\right)}{{\eta }_{tb}}=\frac{4\cdot {10}^{-3}{\left[\frac{Q_c}{Q_{tb}}\right]}^3-1.386{\left[\frac{Q_c}{Q_{tb}}\right]}^2-0.390\left[\frac{Q_c}{Q_{tb}}\right]}{1.0283{\left[\frac{Q_c}{Q_{tb}}\right]}^3-0.5468{\left[\frac{Q_c}{Q_{tb}}\right]}^2+0.5314\left[\frac{Q_c}{Q_{tb}}\right]}$$

(3)

while, for the different relative speeds, the affinity law proposed in [14] is employed

$$\eta \left(V_j\right)=1-\left[1-{\eta }_c\left(Q_c\right)\right]V_j{}^{-0.1}$$

(4)

In Equations (2) and (3), Q_c represents the discharge at the characteristic speed; Q_tb and η_tb are the discharge and the efficiency at the Best Efficiency Point (BEP) of the pump in inverse mode, and are computed from the BEP of the Pump by means of the formula proposed in [15].

The head loss curve at the PAT is computed using the affinity law proposed in [16]

$$\frac{\mathsf{\Delta }H\left(V_j\right)}{H_{tb}}=1.0283{\left[\frac{Q\left(V_j\right)}{Q_{tb}}\right]}^2-0.5468\left[\frac{Q\left(V_j\right)}{Q_{tb}}\right]+0.5314$$

(5)

In Equation (5), the discharge at the relative speed V_j is computed by the classical linear affinity law $Q\left(V_j\right)=Q_c\cdot V_j$, while H_tb, the jump at the best efficiency point, is evaluated with the formula proposed by Yang et al. (2012).

To simulate the bypass of the PAT, the setting V_j = 0 is allowed. When this occurs, Equation (5) is modified by substituting $Q\left(0\right)=Q_c$ and setting $\mathsf{\Delta }H\left(0\right)=0$. In this way, any flow rate can by conveyed without concentrated head loss, as no PAT was present.

2.3.2. Penalty Function

To deal with the problem constraints, the following penalty function is proposed

$$f_{p,k}\left(V\right)={\displaystyle \sum _j^{N_{pat}}\left[P_{Q,k}\left(Q_j\right)+P_{\eta ,k}\left({\eta }_j\right)+P_{V,k}\left(V_j\right)+P_{\mathsf{\Delta }H,k}\left(V_j\right)+P_{H_{\min },k}\left(V_j\right)\right]}$$

(6)

where

$$P_{Q,k}\left(Q_j\right)=\left\{\begin{array}{ll}0;& Q_j\ge 0\\ {\alpha }_Q{V}_j{Q}_j{}^2;& Q_j<0\end{array}\right.$$

(7)

is a penalty function activated when the PAT is oriented opposite to the flow direction;

$$P_{\eta ,k}\left({\eta }_j\right)=\left\{\begin{array}{ll}0;& {\eta }_j\ge 0\\ {\alpha }_{\eta }{V}_j{\eta }_j{}^2;& {\eta }_j<0\end{array}\right.$$

(8)

is a penalty used to discard the settings where Equations (3) or (4) return negative values;

$$P_{V,k}\left(V_j\right)=\left\{\begin{array}{l}0; V_{\min }\le V_j\le 1\\ {\alpha }_V{V}_j{}^2; V_j\in \left]-\infty ,V_{\min }\right[\cup \left]1,\infty \right[\end{array}\right.$$

(9)

is a penalty function that allows the PDS method to choose solutions within the feasible region of settings, while V_min is the minimum relative speed at which the PAT can operate, specified in Section 3;

$$P_{\mathsf{\Delta }H,k}\left(\mathsf{\Delta }{H}_j\right)=\left\{\begin{array}{ll}0;& \mathsf{\Delta }H\le 0\\ {\alpha }_{\mathsf{\Delta }H}{V}_j\mathsf{\Delta }{H}_j{}^2;& \mathsf{\Delta }H>0\end{array}\right.$$

(10)

is a penalty function used to penalize the settings V_j not compatible with the discharge flowing through the pipes, because the external hydraulic solver (EPANET 2.0) gives unphysical results with those settings (i.e., PATs act like pumps to balance the equations of motion);

$$P_{H_{\min },k}\left(H_i\right)={\displaystyle \sum _i^{N_d}{\alpha }_H{V}_j}{\left|\min \left[0,\left(H_i-H_{i,\min }\right)\right]\right|}^2$$

(11)

is the penalty function related to the violation of the minimum head a the i-th demand node of the network, where H_i is the head at the i-th demand node, H_i,min is the minimum head required to fully deliver the user demand, and N_d is the number of demand nodes within the network.

In Equations (7)–(11) the coefficients ${\alpha }_Q$, ${\alpha }_{\eta }$, ${\alpha }_V$, ${\alpha }_{\mathsf{\Delta }H}$ and ${\alpha }_H$ are penalty coefficients. In the present work, the following values were considered: ${\alpha }_Q={\alpha }_{\eta }={\alpha }_{\mathsf{\Delta }H}={10}^6$, ${\alpha }_V={10}^{12}$ and ${\alpha }_H={10}^4$.

3. Application of the Proposed Methodology

In this section, the algorithm described in Section 2 is applied to a case study, and the results are discussed.

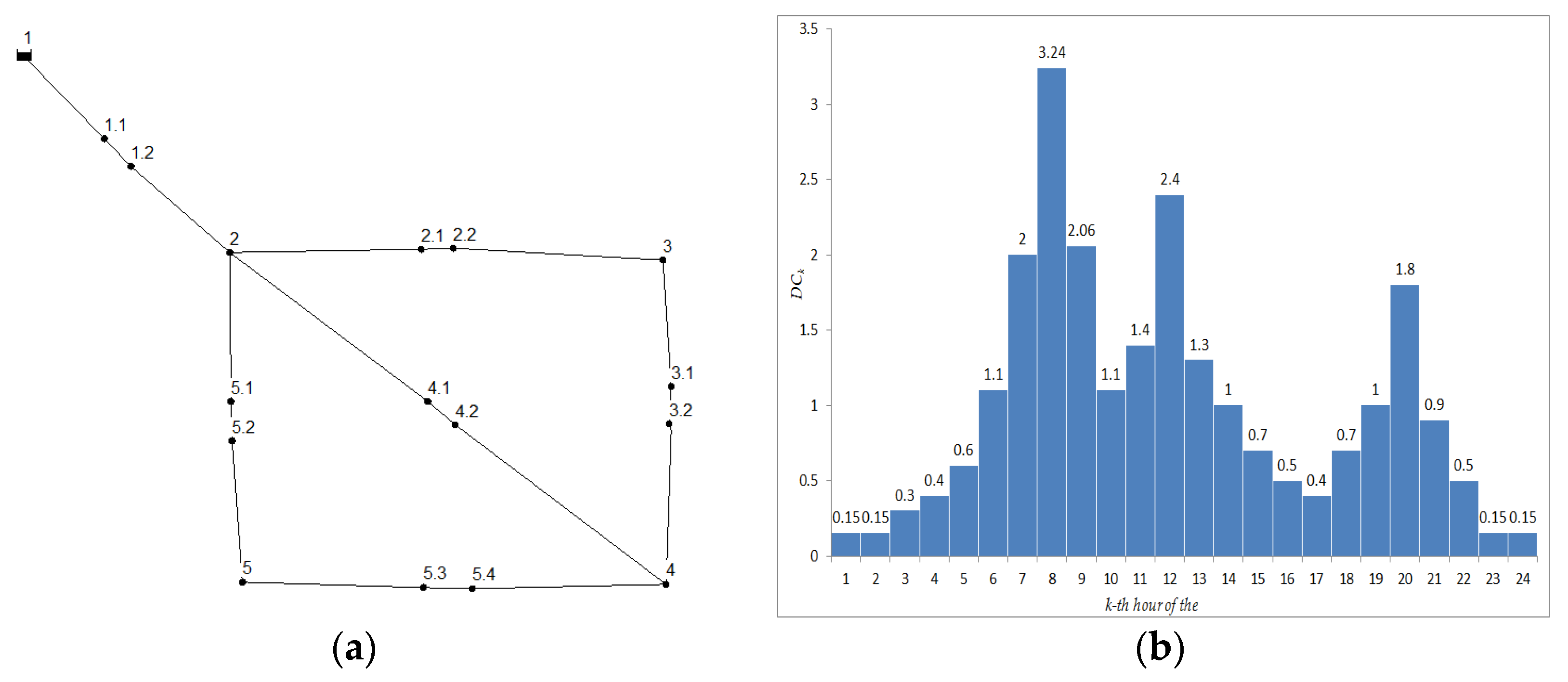
3.1. The Case Study

The case study is a WDN with a simple layout (Figure 1). Nodes and pipes characteristics are reported in

Table 1. Nodes and pipes data of the specified WDN.

Nodes			Pipes
Node ID	Elevation [m]	Demand [l/s]	Node 1	Node 2	Length [m]	Diameter [mm]	Manning coeff.
1	80	0	2.2	3	50	200	0.01
2	16	0	2	2.1	50	200	0.01
3	15	7	2	4.1	60	150	0.01
4	14	7	4.2	4	60	150	0.01
5	13	7	2	5.1	50	150	0.01
2.1	17.5	0	5.2	5	50	150	0.01
2.2	17.5	0	5	5.3	50	100	0.01
4.1	17	0	5.4	4	50	100	0.01
4.2	17	0	4	3.2	50	100	0.01
5.1	16.5	0	3.1	3	50	100	0.01
5.2	16.5	0	1	1.1	300	250	0.01
3.1	14.5	0	1.2	2	1	250	0.01
3.2	14.5	0	3.1	3.2	1	100	0.01
5.3	13.5	0	5.1	5.2	1	150	0.01
5.4	13.5	0	4.1	4.2	1	150	0.01
1.1	16	0	2.1	2.2	1	200	0.01
1.2	16	0	1.1	1.2	1	250	0.01
			5.3	5.4	1	100	0.01

.

Fictitious nodes and pipes have been inserted in the middle of each pipe to locate the PAT. The daily demand coefficient pattern is reported in

Table 2. Results of the three selected scenarios.

Hour	Scenario 1		Scenario 2		Scenario 3
n.	V (1.1 to 1.2)	kWh	V (2.1 to 2.2)	kWh	V (1.1 to 1.2)	V (2.1 to 2.2)	kWh
1	0.103	0.0028	0	0	0.103	0	0.0028
2	0.103	0.0028	0	0	0.103	0	0.0028
3	0.169	0.0286	0	0	0.169	0	0.0286
4	0.229	0.0704	0	0	0.229	0	0.0704
5	0.375	0.251	0	0	0.375	0	0.251
6	0.807	1.6738	0.103	0.01	0.807	0.103	1.6831
7	0.975	9.8045	0.172	0.07	0.975	0	9.8042
8	0.3	2.9992	0.28	0.29	0.3	0	3.0006
9	0.936	10.344	0.177	0.07	0.936	0.467	10.344
10	0.807	1.6738	0.103	0.01	0.807	0.103	1.6831
11	1	3.5964	0.12	0.02	1	0.114	3.6166
12	0.541	9.036	0.207	0.12	0.541	0.545	9.0372
13	0.957	2.8447	0.111	0.02	0.957	0.106	2.8608
14	0.963	1.035	0.103	0.01	0.963	0.103	1.0415
15	0.444	0.4073	0	0	0.444	0.103	0.4088
16	0.307	0.1415	0	0	0.307	0	0.1415
17	0.229	0.0704	0	0	0.229	0	0.0704
18	0.444	0.4073	0	0	0.444	0.103	0.4088
19	0.963	1.035	0.103	0.01	0.963	0.103	1.0415
20	1	7.4998	0.155	0.05	1	0.145	7.5437
21	0.585	0.8969	0	0	0.585	0.103	0.9013
22	0.307	0.1415	0	0	0.307	0	0.1415
23	0.103	0.0028	0	0	0.103	0	0.0028
24	0.103	0.0028	0	0	0.103	0	0.0028

. The PAT considered in this work is the horizontal axis PAT described in [13] with V_min = 0.103 (corresponding to 300 RPM [13]).The maximum discharge circulating within the WDN during the day is 68 l/s, while, in other pipes, the flow is much lower.

Even though the case study is simple, it becomes handy when verifying the capabilities of the algorithm to choose the best rotational speed of the PAT, and to simulate the bypass of the PAT when its use is not recommended.

3.2. Application and Results

The algorithm (Section 2) was applied to the previously described case study for all the possible positions and directions of the single PAT considered. For the sake of brevity and clarity, we selected only the three most relevant scenarios to discuss. By inspection of Figure 1a and Table 1, it is evident that the best location to install a PAT in the pipe from node 1.1 to node 1.2. As a matter of fact, the application of the algorithm to this case returned a solution where the total energy produced is of about 53.97 kWh (Table 2). Conversely, installing the PAT on the same branch but in the opposite direction, the algorithm returned a null setting for each hour of the day (therefore, the PAT was bypassed). By Installing the PAT from node 2.1 to node 2.2, the energy produced during the day was of about 0.665 kWh (Table 2). By installing the PAT in the remaining pipes of the network (in both directions), the algorithm always returned a null setting for every hour of the day. Finally, the PDS was tested with two PATs, and, as expected, the only combination returning settings different from 0 was with PATs installed from node 1.1 to 1.2 and 2.1 to 2.2, with a produced energy of about 54.09 kWh. It is worth noticing that this last outcome is not the simple sum of the energy computed in Scenarios 1 and 2, since the presence of two PATs modifies the flow distribution. In particular, the settings V of the valve from 2.1 to 2.2 are different from those of Scenario 2. Adding a third valve returned null setting in all positions. However, the energy produced by adding an additional PAT in Scenario 1, from 2.1 to 2.2, does not produce more energy. Therefore, the best solution is achieved with only one PAT from node 1.1 to node 1.2.

4. Conclusions

A non-linear programming algorithm for the optimal setting of a PAT was presented. The results showed that the proposed method is able to maximize the energy produced by the PATs installed within a WDN, given their direction, position, and type. In addition, the proposed algorithm was also able to simulate bypass when the PAT position and/or direction was inadequate. The results are promising and the proposed algorithm represents a first step toward the construction of a complete Hybrid Genetic Algorithm able to give back the optimal number, position, direction, type, and setting of PATs to install within a Water Distribution Network to maximize energy production and minimize leakages.