Transparent Object Shape Measurement Based on Deflectometry †
Abstract
:1. Introduction
2. Principle
2.1. Laws of Refraction in Vector Form
2.2. Stereo Normal Vector Consistency Constraint
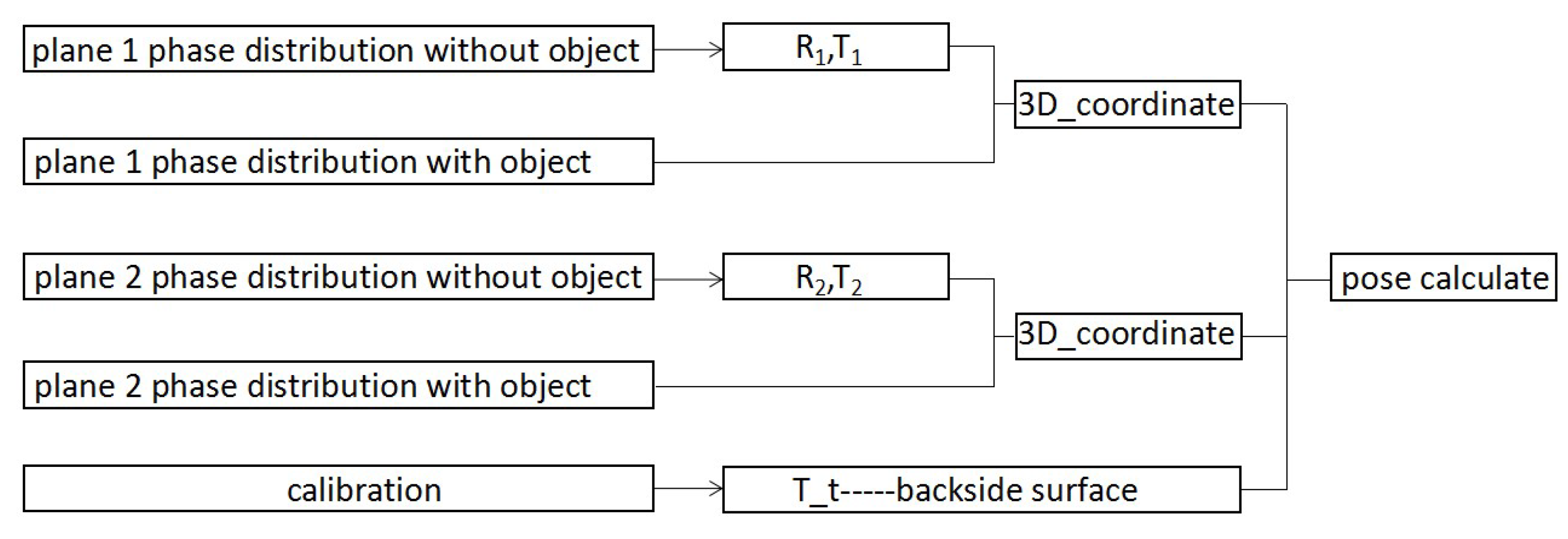
2.3. Pose Calculation
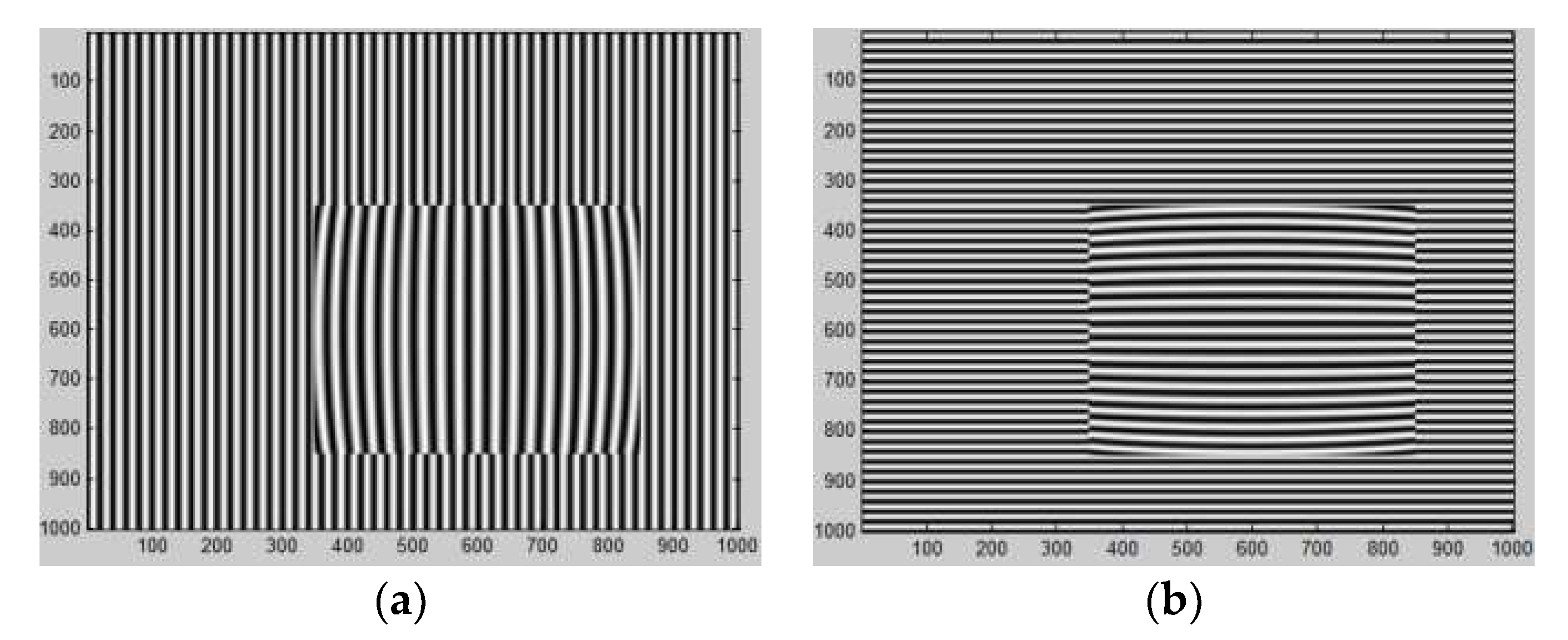
3. Simulation
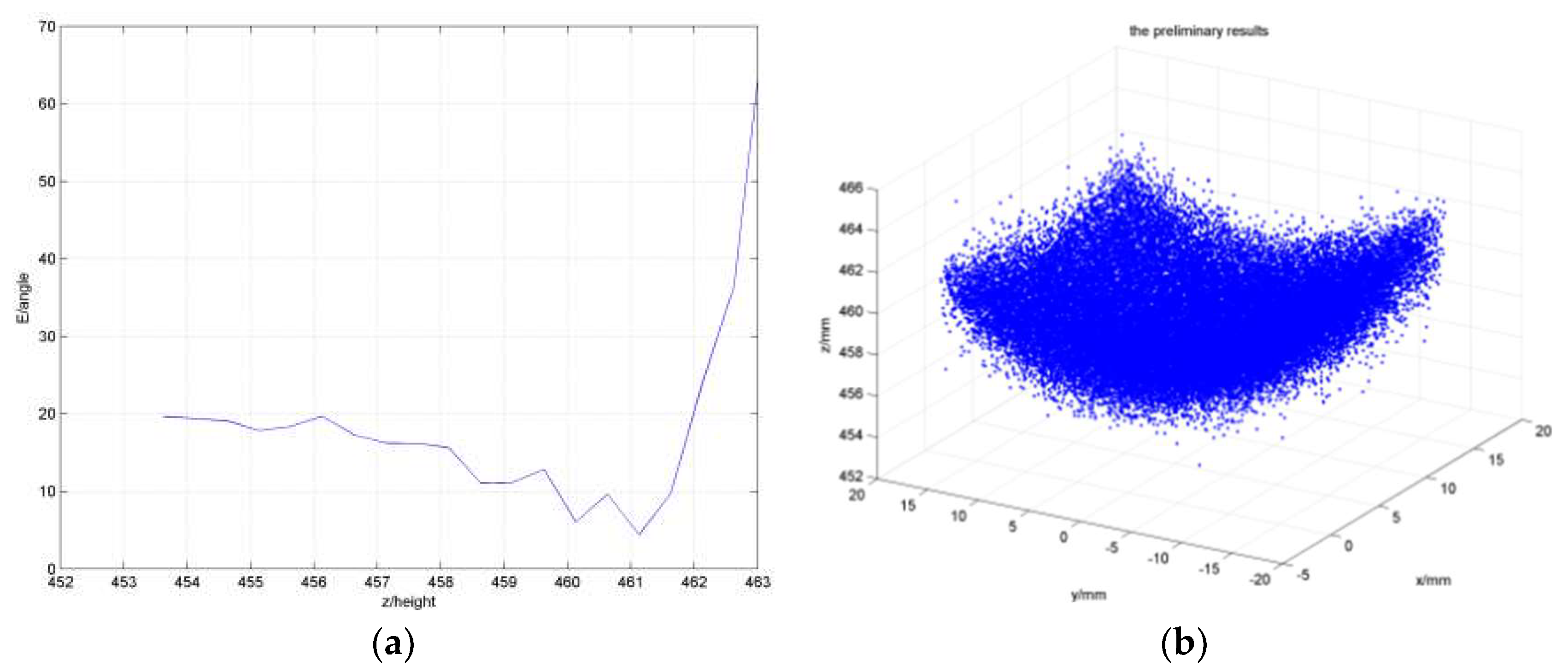
4. Experiment
5. Conclusions
Acknowledgments
References
- Petz, M.; Tutsch, R. Measurement of optically effective surfaces by imaging of gratings. Proc. SPIE Int. Soc. Opt. Eng. 2003, 5, 288–294. [Google Scholar]
- Knauer, M.C.; Hausler, G. Phase measuring deflectometry: A new approach to measure specular free-form surfaces. Proc. SPIE Int. Soc. Opt. Eng. 2004, 5457, 366–376. [Google Scholar]
- Kaminski, J.; Lowitzsch, S.; Knauer, M.C.; Häusler, G. Full-Field Shape Measurement of Specular Surfaces. Fringe 2005; Springer: Berlin/Heidelberg, Germany, 2006; pp. 372–379. [Google Scholar]
- Canabal, H.A.; Alonso, J. Automatic wavefront measurement technique using a computer display and a charge-coupled device camera. Opt. Eng. 2002, 41, 822–826. [Google Scholar] [CrossRef]
- Liu, Y. Research on Key Technology and Application of Phase Measurement Deflection. Ph.D. Thesis, Sichuan University, Chengdu, China, 2007. [Google Scholar]
- Morris, N.J.W.; Kutulakos, K.N. Dynamic Refraction Stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1518–1531. [Google Scholar] [CrossRef] [PubMed]
- Gomit, G.; Chatellier, L.; Calluaud, D.; David, L. Free surface measurement by stereo-refraction. Exp. Fluids 2013, 54, 1540. [Google Scholar] [CrossRef]
- Liu, Y.; Su, X. Camera Calibration method based on Phase Measurement. Opto-Electron. Eng. 2007, 34, 65–69. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Z.; Liu, Y. Transparent Object Shape Measurement Based on Deflectometry. Proceedings 2018, 2, 548. https://doi.org/10.3390/ICEM18-05428
Hao Z, Liu Y. Transparent Object Shape Measurement Based on Deflectometry. Proceedings. 2018; 2(8):548. https://doi.org/10.3390/ICEM18-05428
Chicago/Turabian StyleHao, Zhichao, and Yuankun Liu. 2018. "Transparent Object Shape Measurement Based on Deflectometry" Proceedings 2, no. 8: 548. https://doi.org/10.3390/ICEM18-05428
APA StyleHao, Z., & Liu, Y. (2018). Transparent Object Shape Measurement Based on Deflectometry. Proceedings, 2(8), 548. https://doi.org/10.3390/ICEM18-05428



