A Hybrid Structural Health Monitoring Approach Based on Reduced-Order Modelling and Deep Learning †
Abstract
:1. Introduction
2. SHM Methodology and Fully Convolutional Networks
3. Elastodynamics and Model Order Reduction
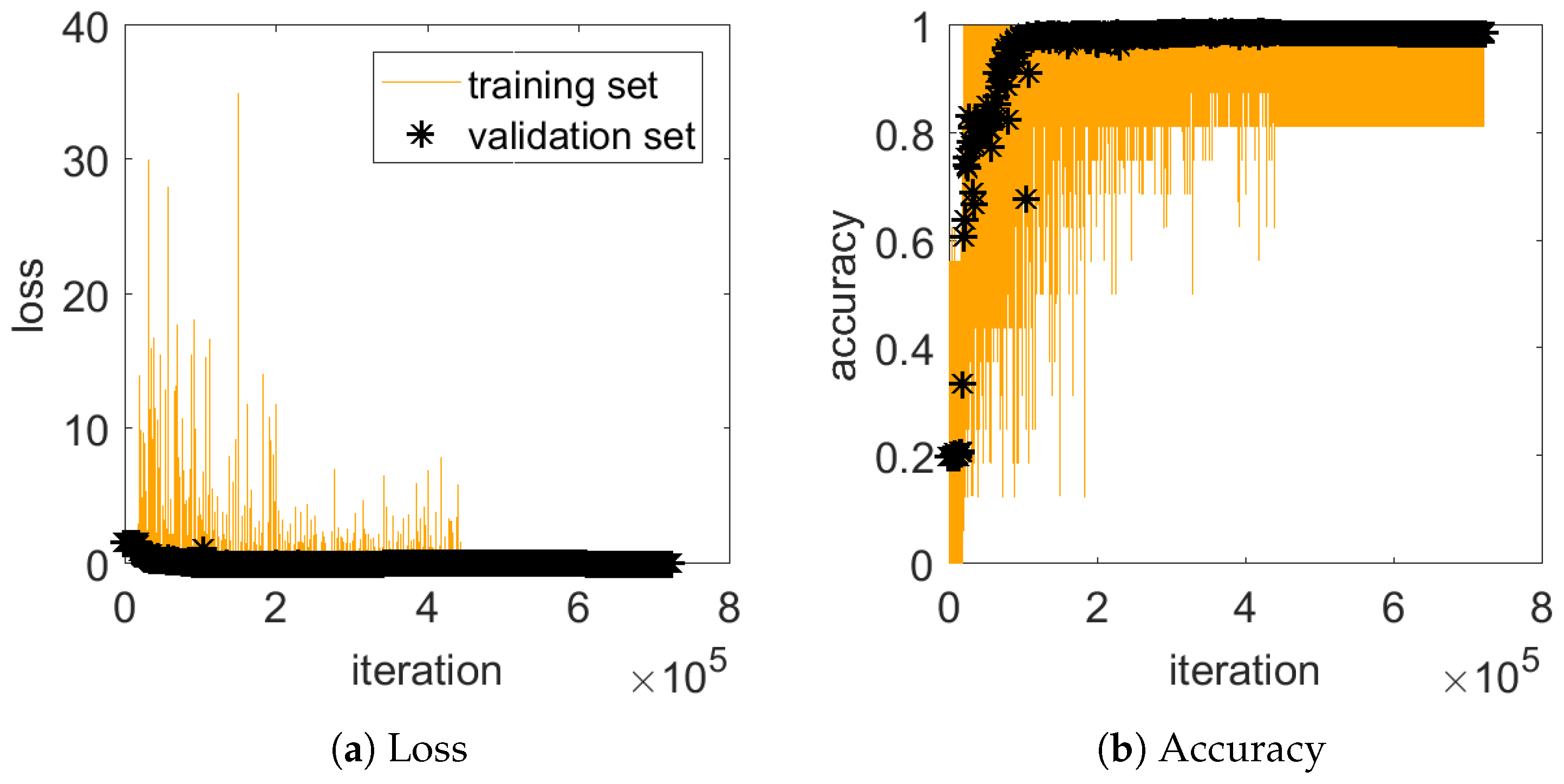
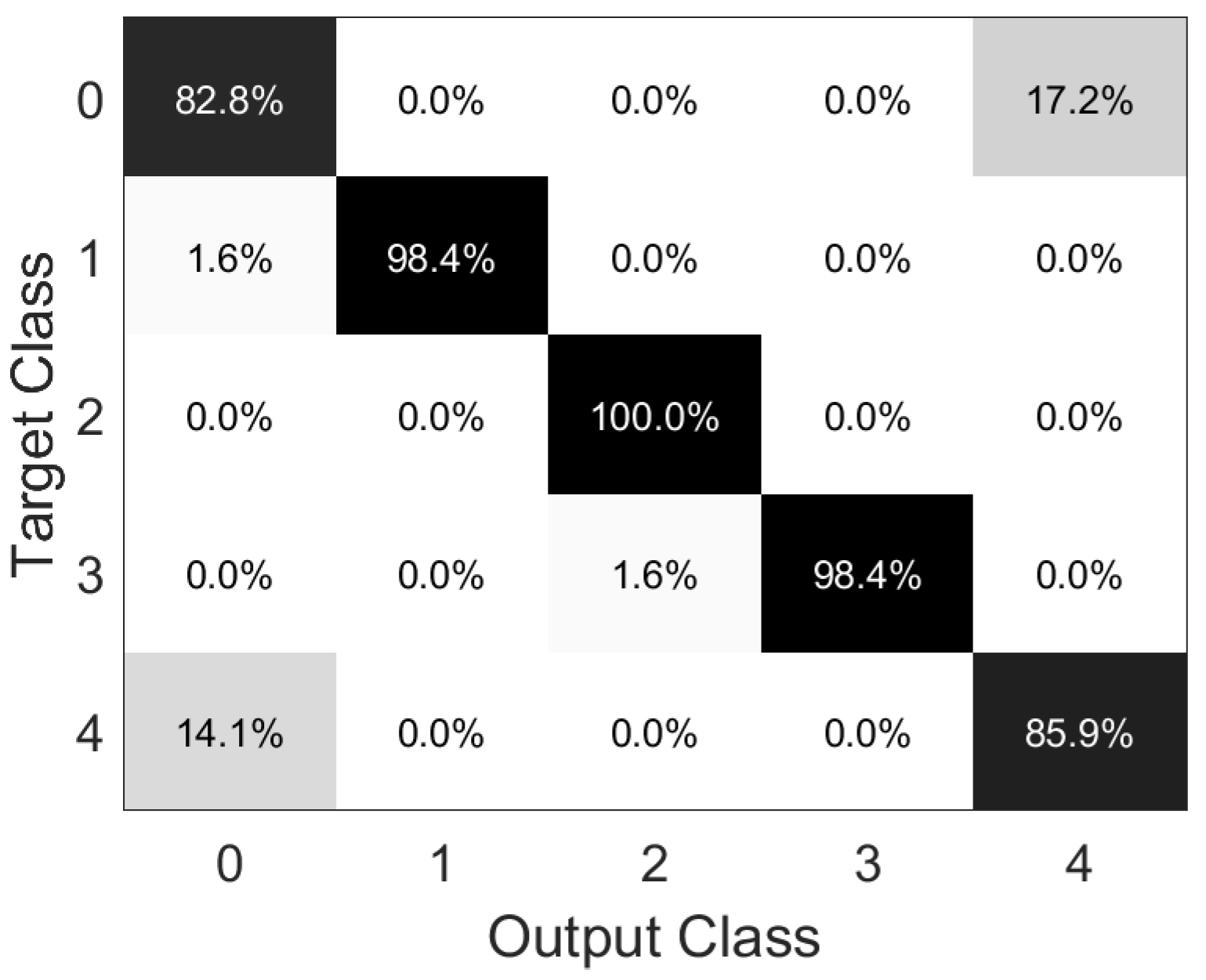
4. Numerical Results
5. Conclusions
Acknowledgments
References
- Chang, P.C.; Flatau, A.; Liu, S.C. Health Monitoring of Civil Infrastructure. Struct. Health Monit. 2003, 2, 257–267. [Google Scholar] [CrossRef]
- Farrar, C.; Worden, K. Structural Health Monitoring A Machine Learning Perspective; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Capellari, G.; Eftekhar Azam, S.; Mariani, S. Damage detection in flexible plates through reduced-order modeling and hybrid particle-Kalman filtering. Sensors 2016, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- Eftekhar Azam, S.; Mariani, S.; Attari, N. Online damage detection via a synergy of proper orthogonal decomposition and recursive Bayesian filters. Nonlinear Dyn. 2017, 89, 1489–1511. [Google Scholar] [CrossRef]
- Eftekhar Azam, S.; Mariani, S. Online damage detection in structural systems via dynamic inverse analysis: A recursive Bayesian approach. Eng. Struct. 2018, 159, 28–45. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibration-Based Structural Damage Identification. Philos. Trans. Math. Phys. Eng. Sci. 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Taddei, T.; Penn, J.; Yano, M.; Patera, A. Simulation-based classification; a model-order-reduction approach for structural health monitoring. Arch. Comput. Methods Eng. 2018, 25, 23–45. [Google Scholar] [CrossRef]
- W. Doebling, S.; Farrar, C.; Prime, M. A Summary Review of Vibration-Based Damage Identification Methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Eftekhar Azam, S.; Mariani, S. Dual estimation of partially observed nonlinear structural systems: A particle filter approach. Mech. Res. Commun. 2012, 46, 54–61. [Google Scholar] [CrossRef]
- Eftekhar Azam, S.; Mariani, S. Investigation of computational and accuracy issues in POD-based reduced order modeling of dynamic structural systems. Eng. Struct. 2013, 54, 150–167. [Google Scholar] [CrossRef]
- Sohn, H.; Worden, K.; Farrar, C.R. Statistical Damage Classification Under Changing Environmental and Operational Conditions. J. Intell. Mater. Syst. Struct. 2002, 13, 561–574. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H. Damage localization under ambient excitations and non-stationary vibration signals by a new hybrid algorithm for feature extraction and multivariate distance correlation methods. Struct. Health Monit. 2019, 18, 347–375. [Google Scholar] [CrossRef]
- Eftekhar Azam, S. Online Damage Detection in Structural Systems; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Milani, R.; Quarteroni, A.; Rozza, G. Reduced basis method for linear elasticity problems with many parameters. Comput. Methods Appl. Mech. Eng. 2008, 197, 4812–4829. [Google Scholar] [CrossRef]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations: An Introduction; Springer: Cham, Switzerland, 2015; Volume 92. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W.; Wang, R. Development and application of a deep learning-based sparse autoencoder framework for structural damage identification. Struct. Health Monit. 2019, 18, 103–122. [Google Scholar] [CrossRef]
- Choy, W.A. Structural Health Monitoring with Deep Learning. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 14–16 March 2018; pp. 557–560. [Google Scholar]
- Capellari, G.; Chatzi, E.; Mariani, S. Structural Health Monitoring Sensor Network Optimization through Bayesian Experimental Design. ASME J. Risk Uncertain. Eng. Syst. Part A: Civ. Eng. 2018, 4, 04018016. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S. Cost–benefit optimization of structural health monitoring sensor networks. Sensors 2018, 18, 2174. [Google Scholar] [CrossRef] [PubMed]
- Rosafalco, L.; Manzoni, A.; Mariani, S.; Corigliano, A. Fully Convolutional Networks for Structural Health Monitoring through Multivariate Time Series Classification. arXiv 2020, arXiv:2002.07032. [Google Scholar] [CrossRef]
- Rosafalco, L.; Corigliano, A.; Manzoni, A.; Mariani, S. Combined Model Order Reduction and Artificial Neural Network for data assimilation and damage detection in structures. In Proceedings of the Computational Sciences and Artificial Intelligence in Industry (CSAI), Jyväskylä (Finland), 12–14 June 2019. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 April 2017; pp. 1578–1585. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Available online: tensorflow.org (accessed on 10 November 2019).
- Haykin, S. Neural Networks and Learning Machines; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS 2010), Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosafalco, L.; Corigliano, A.; Manzoni, A.; Mariani, S. A Hybrid Structural Health Monitoring Approach Based on Reduced-Order Modelling and Deep Learning. Proceedings 2020, 42, 67. https://doi.org/10.3390/ecsa-6-06585
Rosafalco L, Corigliano A, Manzoni A, Mariani S. A Hybrid Structural Health Monitoring Approach Based on Reduced-Order Modelling and Deep Learning. Proceedings. 2020; 42(1):67. https://doi.org/10.3390/ecsa-6-06585
Chicago/Turabian StyleRosafalco, Luca, Alberto Corigliano, Andrea Manzoni, and Stefano Mariani. 2020. "A Hybrid Structural Health Monitoring Approach Based on Reduced-Order Modelling and Deep Learning" Proceedings 42, no. 1: 67. https://doi.org/10.3390/ecsa-6-06585
APA StyleRosafalco, L., Corigliano, A., Manzoni, A., & Mariani, S. (2020). A Hybrid Structural Health Monitoring Approach Based on Reduced-Order Modelling and Deep Learning. Proceedings, 42(1), 67. https://doi.org/10.3390/ecsa-6-06585






