Abstract
Robot mapping and exploration is basic to many robotic applications such as search and rescue operations in disaster scenarios, warehouse management, service robotics, patrolling and autonomous driving. With recent advances in robot navigation and sensor compactness, single robot systems can accurately model the environment and perform complex autonomous navigation tasks. On the other hand, multi-robot systems can speed up mapping and exploration tasks in emergency situations, such as rescue missions, by making use of distributed sensors, thereby increasing the range of exploration tasks to an extent that is not possible with a single robot. Each robot explores and maps different areas of the same environment that are finally merged and connected to make a global map. To build a map of an unknown environment, each robot must perform SLAM, or Simultaneous Localization and Mapping. A big challenge with a multi-robot SLAM system is the transfer of shared map information between multiple robots. There is a possibility of transferring individual measurement errors to the global map, resulting in excess computation and memory required to store such maps. To overcome this problem, we propose to use topological feature map representation that can store information into nodes and edges and does not have any large memory requirements. We present a combined metric-topological mapping approach to multi-robot SLAM. This method maintains a topological pose graph with sensor information stored in nodes and edges that can be optimized globally with reduced information sharing. By combining local metric and topological maps built by individual robots, the reduced graph structure can be merged and extended to map large areas effectively. To robustly merge local maps into global one, we used visual features from each robot that are matched in a distributed system. The graph node-edge structure is used for path planning and navigation. At the same time information sharing between robots results in optimized task distribution between multi-robots.
1. Introduction
Simultaneous Localization and Mapping, or SLAM, is an essential skill for a robot to navigate in unknown environments. The SLAM problem is the backbone for the modern autonomous driving industry and is used for many applications including warehouse robotics, search and rescue and infrastructure maintenance. Single robot SLAM has been extensively studied over the last 20 years and many solutions to the problem have been proposed. Many of these techniques formulate the SLAM problem with probabilistic filters such as the Kalman filter or information filters where the robot poses and features are stored in a large state vector which is continuously updated as the robot explores the area and new landmarks are added to the vector [1,2]. The landmarks can be represented as simple points such as corners, or as defined features such as lines, planes and in the case of cameras as keypoint features that are extracted from the camera images. The complexity of the SLAM problem increases with the type of environment (static and dynamic), and kind of features that are used to determine the environment [3,4,5]. For mapping in indoor environments, a common method is to represent the environment as metric maps, particularly occupied grid maps, where the obstacles and navigable spaces are represented in the grid as occupied or unoccupied cells. SLAM with occupancy grid maps has been presented as fastSLAM, which uses a Rao-blackwellized particle filter [6]. Other methods include representing the environment as features, e.g., lines, planes or point features [7,8,9]. Recently graph based approaches to solving the problem are gaining popularity amongst SLAM researchers [10]. In graph SLAM, the robot’s poses are presented as nodes and edges and the problem is divided into front and back end. While the local SLAM and map corrections are done at the front end, the global optimization is performed as a graph optimization problem at the back end. A brief overview of recent advances in SLAM is presented in [11].
In case of multi-robot systems, the SLAM problem can be regarded as a distributed problem, where each robot performs its own SLAM and their individual maps are finally merged using some method to combine all the features [12,13,14]. The problem is challenging because constraints and errors arising from individual robots will result in a corrupted map and failed localization [15]. Secondly, the computational power required to handle such a complex process of combining maps and correcting pose errors from individual robots into a global map is very high [16]. Communication between the robots is also challenging and algorithms need to be designed such that messages can be transferred seamlessly between the robots [17,18].
Topological maps are another way to represent the environment and have been used by many researchers in the past [19,20]. Topological maps are the simplest of maps where the map information is stored in simple nodes connected by edges. The representation is similar to that of a graph where nodes and edges are used to represent the robot poses and their relations. Another advantage of using topological maps is that the nodes can be used to represent more information about the environment such as semantic features and objects that can be stored into the nodes. Moreover, the memory required to store such topological nodes is very small as compared to metric or graph maps [21].
In this work, we tried to combine the two kinds of information from the map (metric and topological) and used it to solve the multi-robot SLAM problem. Our method uses a reduced graph node structure where the map information is transferred between the robots, resulting in faster map convergence and more consistent maps. We present our results in a simulation environment with two robots equipped with range sensor and camera. Features from the camera are used for semantic representation of the environment, further enhancing the confidence in merging maps.
2. Single Robot Graph Measurement
Each robot in our multi-robot system runs its own pose-graph based approach. The problem reduces to calculating the robot’s position along its trajectory . Each of the poses is represented as a graph connected by edges which represents the constraints between the two poses [22]. Each of the nodes also stores sensor information such as lidar scans. An edge between two poses share odometric measurements coming from wheel encoders. These measurements are represented as Gaussian variable and each of the measurements between the node and by its mean and information matrix . The estimated error can be represented as:
Here, is the sensor measurement, and gives the expected measurement between the two nodes (pose and orientation). The goal of the graph SLAM then becomes a maximum likelihood function whose goal is to minimize the node configuration in the graph given as [23]:
This is a non-linear problem that is solved using a standard optimization algorithm, such as the Levenberg–Marquardt algorithm or the Gauss–Newton method [23].
A problem with directly transferring the node and edges or the graph to other robots in the multi-robot system poses a lot of challenges, as stated earlier. Firstly, errors in an individual graph can be translated as it is to other robots and a mismatch may result in a large deflection (error) in the combined graph. Secondly, transferring all the nodes will result in a large graph that requires more computation to optimize at backend, and in general would distort the graph. To solve this problem we propose to use the graph nodes with topological format (information).
Topological Formulation
The topological map is represented as a graph tuple made of nodes, and edges [19,21]. An additional change is that every node stored in stores more information about the type of edges and sensor information such as image and image matching features and surroundings (room, corridor, etc.) classified by region geometry. Every node in the topological node is unique and is assigned only once per node. A node can be associated to different areas in the map for semantic representation. Other available information can be added to the node depending on the region and its properties including objects. The drawback, however, is an increase in the computation cost to store all nodes.
3. Multi-Robot SLAM
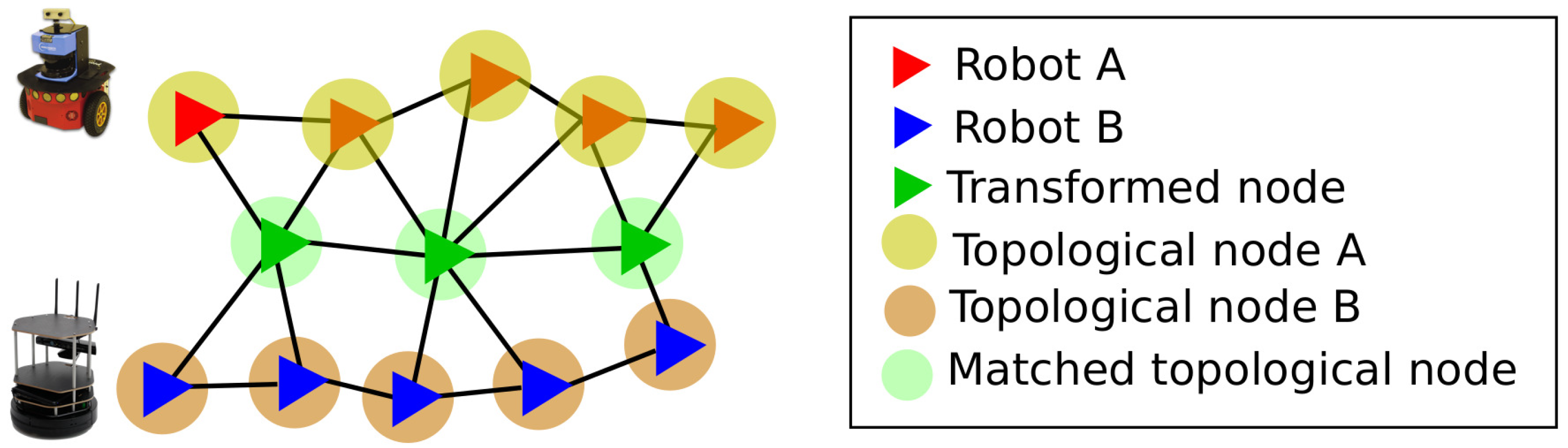
Once all the robots have built their own topological graph SLAM, information can be shared across different robots. To reduce the burden of sharing all node information, a reduced graph approach is proposed that can fasten the search and merging process. Only nodes that share similar properties from the semantic information including robust matching of features such as SIFT or SURF are shared among the encountered robots. Consider a situation as shown in Figure 1. Two robots A and B explore different areas of the same map and run their own SLAM algorithm. When robot A comes within the communication range of robot B, the information sharing is triggered by ping messages between the two. Nodes are shared based on scan matching parameters of range sensor data. Image matching between robot A and robot B is performed to check if the robot has seen the place before. The topological information in nodes, and semantic information (e.g., whether the area is a corridor, or a particular room) that is previously stored in the nodes are matched and confirmed. After enough confidence is built across the two robots, they start to accept the nodes into their own graph and update the overall graph through optimization where the transformation between the two robot (A and B) poses are determined. Only nodes in the area of search are shared among the robots, thereby reducing the number of nodes that are shared. This is done through our semantic topological node matching. When the confidence level reaches the theshhold value that is set by the user, other nodes can be shared to validate the missing information from the map. Optimization at this time takes place in both the robots, such that each robot has the updated information about the environment. Our proposed method allows the robots to share the information in real-time in wifi networks since the size of shared information is within the limit of real-time performance. Each robot can use the shared graph for robust localization using the merged pose graph and range sensor scan matching [8].
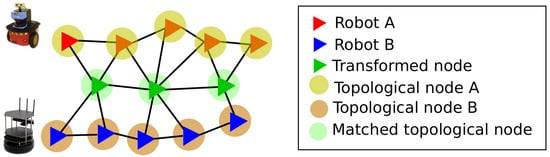
Figure 1.
Multi-robot Simultaneous Localization and Mapping (SLAM) process. Robots A and B send the node information for sharing, shown in green. Their respective topological nodes are shown as circles.
4. Results
To test the proposed idea, preliminary experiments were performed using two robots in a simulated environment. The simulation environment consists of many room-like environments connected by long corridors that resemble office areas. The environment was constructed using the Gazebo simulator. All computations were performed on a single laptop PC with core i7 processor and 16 GB of RAM. The Robot Operating System (ROS) was used for programming and data collection. The robots were equipped with range sensors and camera sensors, and wheel odometries from respective robots were used to measure odometry.
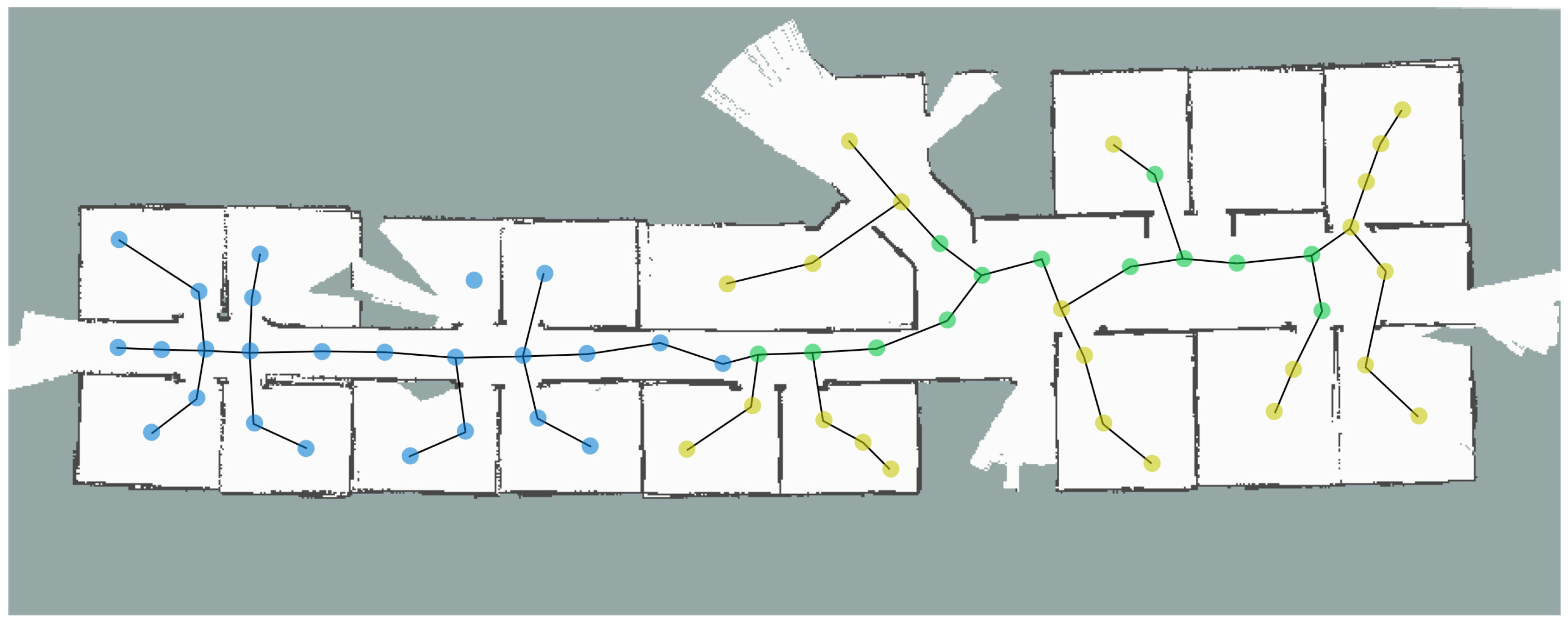
Each robot ran its own topological graph SLAM and the communication was set up to mimic a wifi environment where the robots can share information once they are within each other’s communication range. Robot A’s trajectory and topological graph nodes are shown in yellow and B’s are shown in blue in Figure 2. Each robot started exploration at the opposite end of the map and run its own mapping algorithm. The grid map representation of the environment is shown in Figure 2. Robot B was programmed to enter into Robot A’s area at some point and the node sharing process was initiated. The transformation was checked by matching image features and range sensor scan matching and, based on this data, transformation between the two nodes was calculated and merged as common nodes (shown in green). The final merged grid (metric) map is shown in the background as a complete map. As can be seen from the Figure 2, the map is correctly merged and can be used for multi-robot task coordination and task sharing [24]. The merging process takes instantly and all the information is shared across different agents in the team. This allows the robots to share common resources, have information about obstacles and closed areas in the map and ability to plan faster and optimum routes when planning.
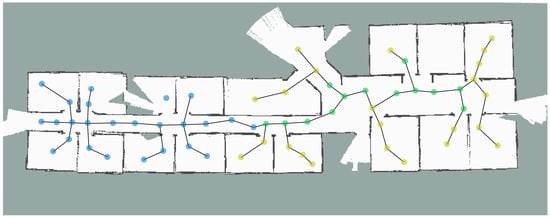
Figure 2.
Multi-robot experiment. Robot A’s nodes are presented in yellow and Robot B’s in blue. The green nodes are the common or shared nodes between the two robots and the merged map is presented as a grid map.
5. Conclusions
This paper presents a method of multi-robot SLAM and exploration using a reduced graph and topological information. Our proposed method matches and merges nodes coming from individual robots into a reduced graph and outputs a merged optimized graph and map. The process only considers nodes in the vicinity of the robot and therefore is computationally efficient. Results were shown in the simulation environment and the results confirm the effectiveness of the proposed framework. The results shown in this work are only in simulated environment with two or three robots. From the preliminary tests, the algorithm works fine for small to medium size environment, however more tests in complex and real environment is required to check the efficiency of our proposed method. In the future, we will test the proposed idea in a real environment with actual robots.
Author Contributions
A.A.R. and A.R. conceived the idea, performed the experiments, and developed the algorithm for the multi-robot SLAM. T.E. and Y.K. provided suggestions to analyze data and improve the manuscript. The article was written by A.A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics (Intelligent Robotics and Autonomous Agents); The MIT Press: Cambridge, CA, USA, 2005. [Google Scholar]
- Dissanayake, M.W.M.G.; Newman, P.; Clark, S.; Durrant-Whyte, H.F.; Csorba, M. A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans. Robot. Autom. 2001, 17, 229–241. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. SHP: Smooth Hypocycloidal Paths with Collision-Free and Decoupled Multi-Robot Path Planning. Int. J. Adv. Robot. Syst. 2016, 13, 133. [Google Scholar] [CrossRef]
- Huang, S.; Dissanayake, G. Convergence and consistency analysis for extended Kalman filter based SLAM. IEEE Trans. Robot. 2007, 23, 1036–1049. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Symbiotic navigation in multi-robot systems with remote obstacle knowledge sharing. Sensors 2017, 17, 1581. [Google Scholar] [CrossRef] [PubMed]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges. In Proceedings of the IJCAI, Acapulco, Mexico, 9–15 August 2003; pp. 1151–1156. [Google Scholar]
- Ravankar, A.A.; Hoshino, Y.; Ravankar, A.; Jixin, L.; Emaru, T.; Kobayashi, Y. Algorithms and a framework for indoor robot mapping in a noisy environment using clustering in spatial and hough domains. Int. J. Adv. Robot. Syst. 2015, 12, 27. [Google Scholar] [CrossRef]
- Wang, Y.T.; Peng, C.C.; Ravankar, A.; Ravankar, A. A Single LiDAR-Based Feature Fusion Indoor Localization Algorithm. Sensors 2018, 18, 1294. [Google Scholar] [CrossRef] [PubMed]
- Ravankar, A.; Ravankar, A.A.; Hoshino, Y.; Emaru, T.; Kobayashi, Y. On a hopping-points svd and hough transform-based line detection algorithm for robot localization and mapping. Int. J. Adv. Robot. Syst. 2016, 13, 98. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M. The graph SLAM algorithm with applications to large-scale mapping of urban structures. Int. J. Robot. Res. 2006, 25, 403–429. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Cunningham, A.; Paluri, M.; Dellaert, F. DDF-SAM: Fully distributed SLAM using constrained factor graphs. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3025–3030. [Google Scholar]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. On a bio-inspired hybrid pheromone signalling for efficient map exploration of multiple mobile service robots. Artif. Life Robot. 2016, 21, 221–231. [Google Scholar] [CrossRef]
- Saeedi, S.; Trentini, M.; Seto, M.; Li, H. Multiple-robot simultaneous localization and mapping: A review. J. Field Robot. 2016, 33, 3–46. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Hitchhiking robots: A collaborative approach for efficient multi-robot navigation in indoor environments. Sensors 2017, 17, 1878. [Google Scholar] [CrossRef] [PubMed]
- Labbe, M.; Michaud, F. Online global loop closure detection for large-scale multi-session graph-based SLAM. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2661–2666. [Google Scholar]
- Roumeliotis, S.I.; Bekey, G.A. Distributed multi-robot localization. In Distributed Autonomous Robotic Systems 4; Springer: Tokyo, Japan, 2000; pp. 179–188. [Google Scholar]
- Leung, K.Y.; Barfoot, T.D.; Liu, H.H. Distributed and decentralized cooperative simultaneous localization and mapping for dynamic and sparse robot networks. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3841–3847. [Google Scholar]
- Chang, H.J.; Lee, C.G.; Hu, Y.C.; Lu, Y.H. Multi-robot SLAM with topological/metric maps. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1467–1472. [Google Scholar]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Semantic Navigation for Indoor Service Robots. In Proceedings of the JSME annual Conference on Robotics and Mechatronics (Robomec) 2018; The Japan Society of Mechanical Engineers: Tokyo, Japan, 2018; pp. 1P1–G01. [Google Scholar]
- Ravankar, A.A.; Ravankar, A.; Emaru, T.; Kobayashi, Y. A hybrid topological mapping and navigation method for large area robot mapping. In Proceedings of the 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017; pp. 1104–1107. [Google Scholar]
- Sünderhauf, N.; Protzel, P. Towards a robust back-end for pose graph slam. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1254–1261. [Google Scholar]
- Grisetti, G.; Kummerle, R.; Stachniss, C.; Burgard, W. A tutorial on graph-based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Ravankar, A.A.; Ravankar, A.; Peng, C.C.; Kobayashi, Y.; Emaru, T. Task coordination for multiple mobile robots considering semantic and topological information. In Proceedings of the 2018 IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 1088–1091. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).