Interpreting the High Energy Consumption of the Brain at Rest †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hypothesis Background
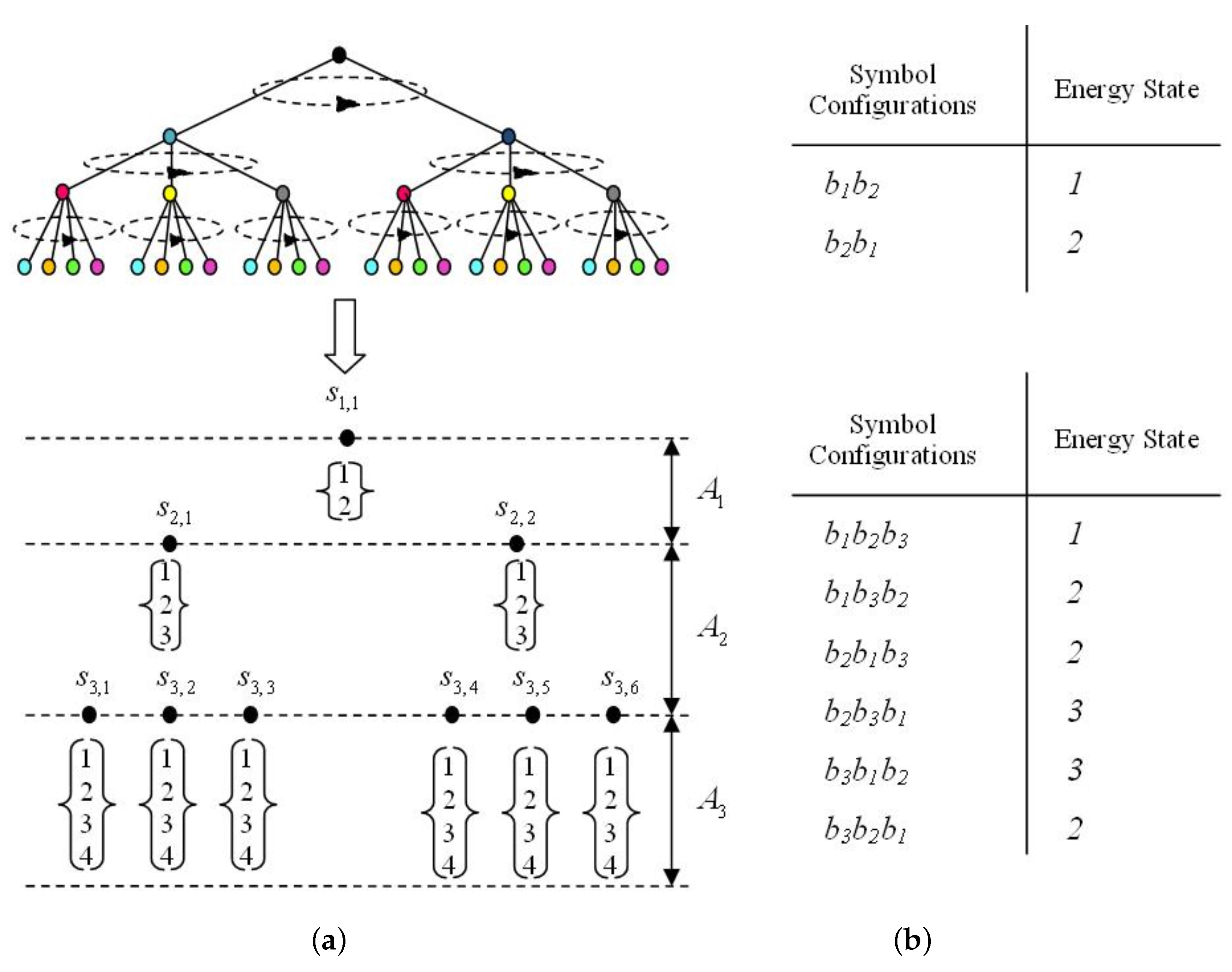
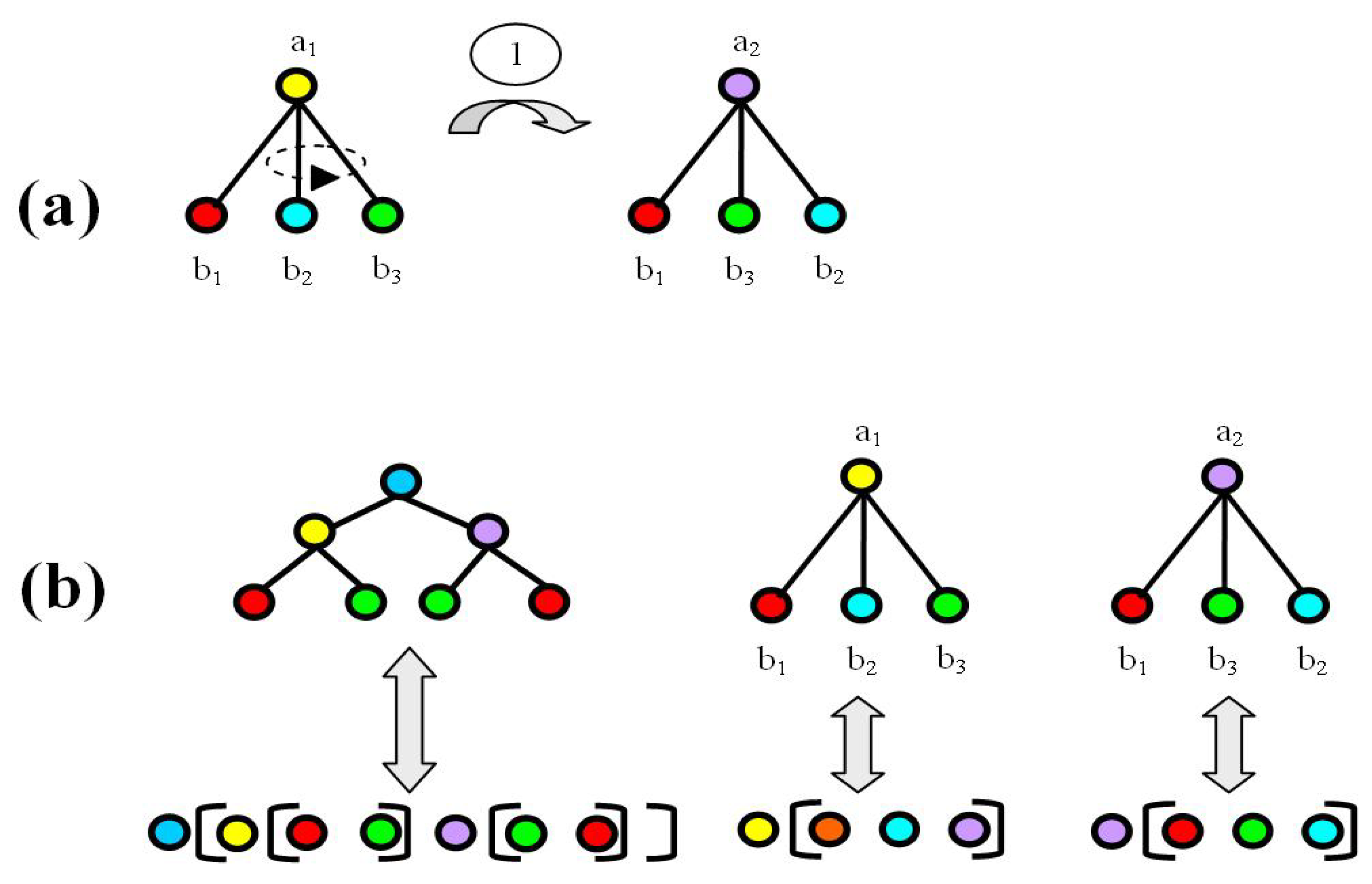
2.2. The Energy Model
3. Results
3.1. Most Probable State Analysis
4. Discussion
4.1. Implications for Neuroscience Research
5. Conclusions
Funding
Conflicts of Interest
Abbreviations
| ATP | Adenosine Triphosphate |
Appendix A. Definitions and Notations
Appendix B. Derivation of Equations
References
- Boly, M.; Phillips, C.; Tshibanda, L.; Vanhaudenhuyse, A.; Schabus, M.; Dang-Vu, T.T.; Moonen, G.; Hustinx, R.; Maquet, P.; Laureys, S. Intrinsic Brain Activity in Altered States of Consciousness How Conscious is the Default Mode of Brain Function? Ann. N. Y. Acad. Sci. 2008, 1129, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Buckner, R.L.; Vincent, J.L. Unrest at rest: Default activity and spontaneous network correlations. NeuroImage 2007, 37, 1091–1096. [Google Scholar] [CrossRef] [PubMed]
- Gusnard, D. A, Raichle, M.E. Searching for a baseline: Functional Imaging and the Resting Human Brain. Nat. Rev. Neurosci. 2001, 2, 685–694. [Google Scholar] [CrossRef] [PubMed]
- Morcom, A.M.; Fletcher, P.C. Does the brain have a baseline? Why we should be resisting a rest. NeuroImage 2007, 37, 1073–1082. [Google Scholar] [CrossRef] [PubMed]
- Shulman, R. G, Hyder, F.; Rothman D.L. Baseline brain energy supports the state of consciousness. Proc. Natl. Acad. Sci. USA 2009, 106, 11096–11101. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 6th ed.; Macmillan Learning Publishers: New York, NY, USA, 2012. [Google Scholar]
- Churchland, P.; Sejnowski, T. The Computational Brain; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Mead, C. Analog VLSI and Neural Systems; Addison Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Ingvar, D.H. “Memory of the future”: An essay on the temporal organization of conscious awareness. Hum. Neurobiol. 1985, 4, 127–136. [Google Scholar] [PubMed]
- Tulving, E. The Missing Link in Cognition: Origins of Self-Reflective Consciousness; Terrace, H.S., Ed.; Oxford University Pres: New York, NY, USA, 2005. [Google Scholar]
- Gusnard, D.A.; Raichle, M.E. Intrinsic functional architecture in the anesthetized monkey brain. Nature 2007, 447, 83–86. [Google Scholar]
- Chinea, A. Is Cetacean Intelligence Special? New Perspectives on the Debate. Entropy 2017, 19, 543. [Google Scholar] [CrossRef]
- Chinea, A.; Korutcheva, E. Intelligence and Embodiment: A Statistical Mechanics Approach. Neural Netw. 2013, 40, 52–72. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Reichl, L.E. A Modern Course in Statistical Physics; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Hecht-Nielsen, R. Confabulation Theory: The Mechanism of Thought; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Taylor, P.; Hobbs, J.N.; Burroni, J.; Siegelmann, H. The global landscape of cognition:hierarchical aggregation as an organizational principle of human cortical networks and functions. Sci. Rep. 2015, 5, 18112. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Y.; Slotine, J.J.; Barabasi, A.L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Harris, J.J.; Jolivet, R.; Engl, E.; Atwell, D. Energy-Efficient Information Transfer by Visual Pathway Synapses. Curr. Biol. 2015, 25, 3151–3160. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, S.B.; de Ruyter van Steveninck, R.R.; Anderson, J.C. The metabolic cost of neural information. Nat. Neurosci. 1998, 1, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Niven, J.E.; Laughlin, S.B. Energy imitation as selective pressure on the evolution of sensory systems. J. Exp. Biol. 2008, 211, 1792–1804. [Google Scholar] [CrossRef] [PubMed]
- Striedter, G.F. Principles of Brain Evolution; Sinauer Associates, Inc.: Sunderland, MA, USA, 2005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Lara, A.C.M. Interpreting the High Energy Consumption of the Brain at Rest. Proceedings 2020, 46, 30. https://doi.org/10.3390/ecea-5-06694
de Lara ACM. Interpreting the High Energy Consumption of the Brain at Rest. Proceedings. 2020; 46(1):30. https://doi.org/10.3390/ecea-5-06694
Chicago/Turabian Stylede Lara, Alejandro Chinea Manrique. 2020. "Interpreting the High Energy Consumption of the Brain at Rest" Proceedings 46, no. 1: 30. https://doi.org/10.3390/ecea-5-06694
APA Stylede Lara, A. C. M. (2020). Interpreting the High Energy Consumption of the Brain at Rest. Proceedings, 46(1), 30. https://doi.org/10.3390/ecea-5-06694




