Fully Coupled Modeling of Athlete Force Application and Power Transfer in Rowing Ergometry †
Abstract
:1. Introduction
2. Methods
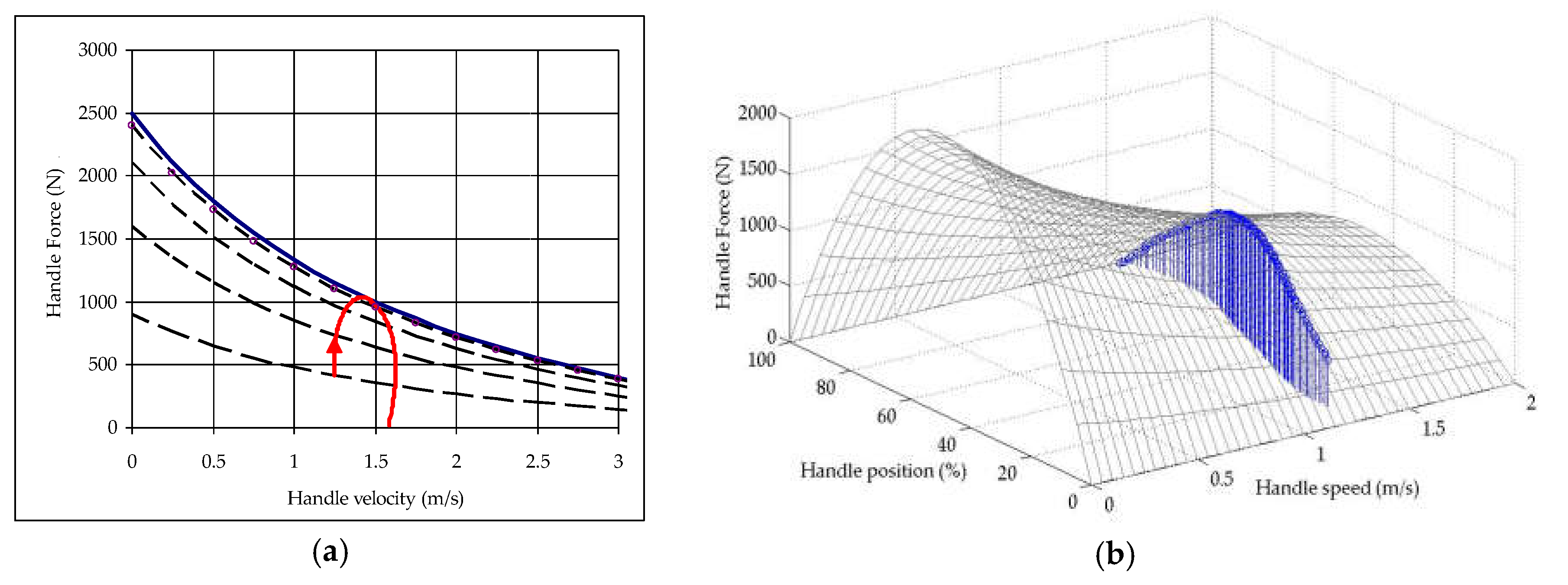
2.1. Muscle Force-Velocity-Length Model
Fapp(v,l) = 4 Fmax l (1 − l)
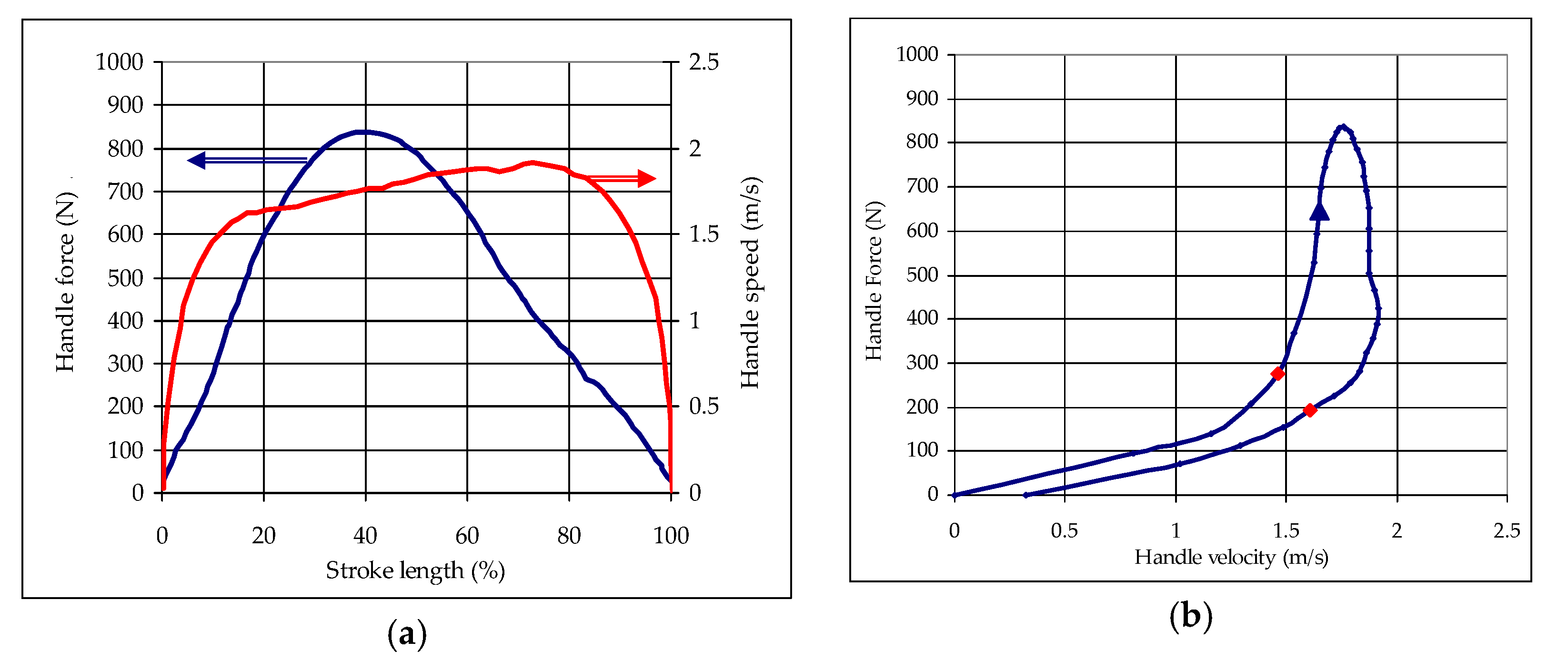
2.2. Kleshnev (2006) Measurements
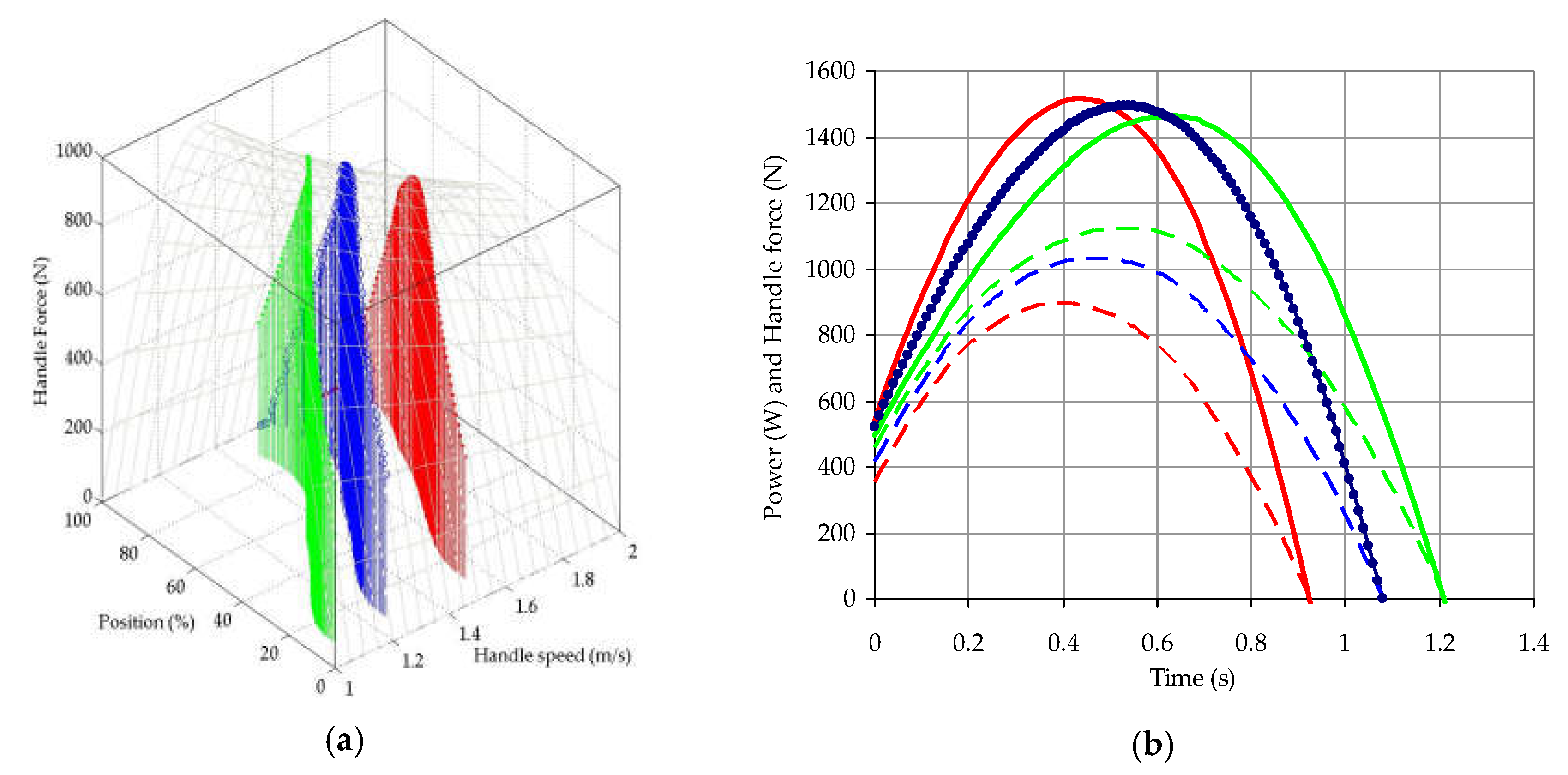
3. Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hartmann, U.; Mader, A.; Wasser, K.; Klauer, I. Peak force, velocity, and power during five and ten maximal rowing ergometer strokes by world class female and male rowers. Intl. J. Sports Med. 1993, 14, S42–S45. [Google Scholar] [CrossRef] [PubMed]
- Sprague, R.C.; Martin, J.C.; Davidson, C.J.; Farrrar, R.P. Force–Velocity and Power–Velocity Relationships during Maximal Short-Term Rowing Ergometry. Med. Sci. Sports Exerc. 2007, 39, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Vandewalle, H.; Peres, G.; Heller, J.; Panel, J.; Monod, H. Force-velocity relationship and maximal power on a cycle ergometer. Eur. J. Appl. Physiol. 1987, 56, 358–364. [Google Scholar] [CrossRef] [PubMed]
- Coast, J.R.; Cox, R.H.; Welsh, H.G. Optimal pedalling rate in prolonged bouts of cycle ergometry. Med. Sci. Sports Exerc. 1986, 18, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Marsh, A.P.; Martin, P.E.; Foley, K.O. Effect of cadence, cycling experience, and aerobic power on delta efficiency during cycling. Med. Sci. Sports Exerc. 2000, 32, 1630–1634. [Google Scholar] [CrossRef] [PubMed]
- Ansley, L.; Cangley, P. Determinants of ‘‘optimal’’ cadence during cycling. Eur. J. Sport Sci. 2009, 2, 61–85. [Google Scholar] [CrossRef]
- Sliasas, A.; Tullis, S. The dynamic flow behaviour of an oar blade in motion using a hydrodynamics-based shell-velocity-coupled model of a rowing stroke. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2010, 224, 9–24. [Google Scholar] [CrossRef]
- Concept2 Ergometers. Available online: www.concept2.com/indoor-rowers (accessed on 30 September 2019).
- Kleshnev, V. Comparison of on-water rowing with its simulation on Concept2 and Rowperfect machines. In Proceedings of the International Society of Biomechanics in Sports XXIII Conference, Beijing, China, 22–27 August 2005; pp. 130–133. [Google Scholar]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. B 1938, 126, 136–195. [Google Scholar]
- Huijing, P.A. Muscle as a collagen fiber reinforced composite: A review of force transmission in muscle and whole limb. J. Biomech. 1999, 32, 329–345. [Google Scholar] [CrossRef]
- Gordon, A.M.; Huxley, A.F.; Julian, F.J. The variation in isometric tension with sacromere length in vertebrete muscle fibres. J. Physiol. 1966, 184, 170–192. [Google Scholar] [CrossRef] [PubMed]
- Wickiewicz, T.L.; Roy, R.R.; Powell, P.L.; Perrine, J.J.; Edgerton, V.R. Muscle architecture and force-velocity relationships in humans. J. App. Physiol. 1984, 57, 435–443. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, A.; Viale, F.; Dalleau, G.; Lacour, J. Force/velocity and power/velocity relationships in squat exercise. Eur. J. Appl. Physiol. 2001, 84, 227–232. [Google Scholar] [CrossRef] [PubMed]
| Hill Model Parameter | Value | Ergometer Parameter | Value |
|---|---|---|---|
| Fiso | 2500 N | Flywheel rotational inertia (I) | 0.2 kg·m2 |
| a | 1000 N | Aerodynamic drag factor (k) | 0.001 Nm·s2 |
| b | 2 (m/s) | Ratchet cog gearing | 61.8 rad/s per m/s |
| lcatch | 0.1 | Athlete mass | 72.2 kg |
| lfinish | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tullis, S.; Galipeau, C. Fully Coupled Modeling of Athlete Force Application and Power Transfer in Rowing Ergometry. Proceedings 2020, 49, 108. https://doi.org/10.3390/proceedings2020049108
Tullis S, Galipeau C. Fully Coupled Modeling of Athlete Force Application and Power Transfer in Rowing Ergometry. Proceedings. 2020; 49(1):108. https://doi.org/10.3390/proceedings2020049108
Chicago/Turabian StyleTullis, Stephen, and Cameron Galipeau. 2020. "Fully Coupled Modeling of Athlete Force Application and Power Transfer in Rowing Ergometry" Proceedings 49, no. 1: 108. https://doi.org/10.3390/proceedings2020049108
APA StyleTullis, S., & Galipeau, C. (2020). Fully Coupled Modeling of Athlete Force Application and Power Transfer in Rowing Ergometry. Proceedings, 49(1), 108. https://doi.org/10.3390/proceedings2020049108





