Use of an Inertial Measurement System to Calculate Maximal Power during Running Sprint Acceleration: Comparison with the Radar System †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Protocol
2.3. Data Processing
2.4. Statistical Analyses
3. Results
3.1. Velocity Time Relationship
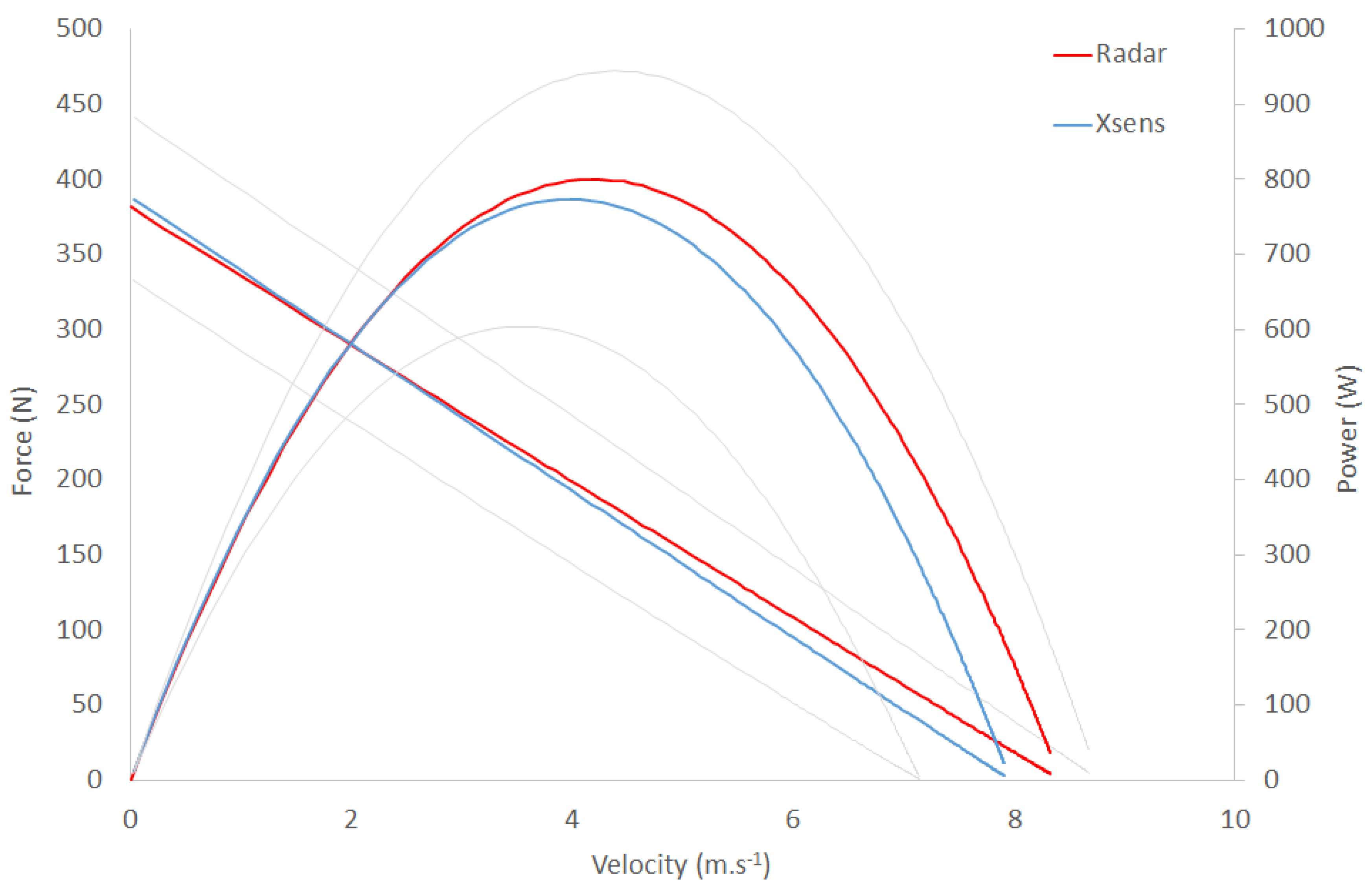
3.2. F-v and P-v Relationships
4. Discussion
5. Conclusions
Conflicts of Interest
References
- Rabita, G.; Dorel, S.; Slawinski, J.; Sàez-de-Villarreal, E.; Couturier, A.; Samozino, P.; Morin, J.B. Sprint mechanics in world-class athletes: A new insight into the limits of human locomotion. Scand. J. Med. Sci. Sports 2015, 25, 583–594. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.; Samozino, P.; Edouard, P. Effectiveness of force application in sprint running: Definition of concept and relationship with performance. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 173–175. [Google Scholar] [CrossRef]
- Slawinski JTermoz, N.; Rabita, G.; Guilhem, G.; Dorel, G.; Morin, J.B.; Samozino, P. How 100-m event analyses improve our understanding of world-class men’s and women’s sprint performance. Scand. J. Med. Sci. Sports. 2017, 27, 45–54. [Google Scholar] [CrossRef]
- Morin, J.B.; Samozino, P.; Murata, M.; Cross, M.; Nagahara, R. A simple method for computing sprint acceleration kinetics from running velocity data: Replication study with improved design. J. Biomech. 2019, 94, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Rabita, G.; Dorel, S.; Slawinski, J.; Peyrot, N.; De Villarreal, E.; Morin, J.B. A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand. J. Med. Sci. Sports 2016, 26, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Slawinski, J.; Bonnefoy, A.; Ontanon, G.; Leveque, J.M.; Miller, C.; Riquet, A.; Chèze, L.; Dumas, R. Segment-interaction in sprint start: Analysis of 3D angular velocity and kinetic energy in elite sprinters. J. Biomech. 2010, 43, 1494–1502. [Google Scholar] [CrossRef] [PubMed]
- Dinu, D.; Fayolas, M.; Jacquet, M.; Leguy, E.; Slawinski, J.; Houel, N. Accuracy of Postural Human-motion Tracking Using Miniature Inertial Sensors. Procedia Eng. 2016. [Google Scholar] [CrossRef]
- Blair, S.; Duthie, G.; Robertson, S.; Hopkins, W.; Ball, K. Concurrent validation of an inertial measurement system to quantify kicking biomechanics in four football codes. J. Biomech. 2018, 73, 24–32. [Google Scholar] [CrossRef] [PubMed]
- di Prampero, P.E.; Botter, A.; Osgnach, O. The energy cost of sprint running and the role of metabolic power in setting top performances. Eur. J. Appl. Physiol. 2015, 115, 451–469. [Google Scholar] [CrossRef] [PubMed]
- Jimenez-reyes, P.; Cuadrado, V. Differences in sprint mechanical force-velocity profile between trained soccer and futsal players. J. Sport. Physiol. Perform. 2019, 14, 478–485. [Google Scholar] [CrossRef] [PubMed]
- Helland, C.; Haugen, T.; Rakovic, E.; Eriksrud, O.; Seynnes, O.; Mero, A.A.; Paulsen, G. Force–velocity profiling of sprinting athletes: Single-run vs. multiple-run methods. Eur. J. Appl. Physiol. 2019, 119, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Slawinski, J.; Billat, V.; Koralsztein, J.P.; Tavernier, M. Use of lumbar point for the estimation of potential and kinetic mechanical power in running. J. Appl. Biomech. 2004, 20, 324–331. [Google Scholar] [CrossRef]
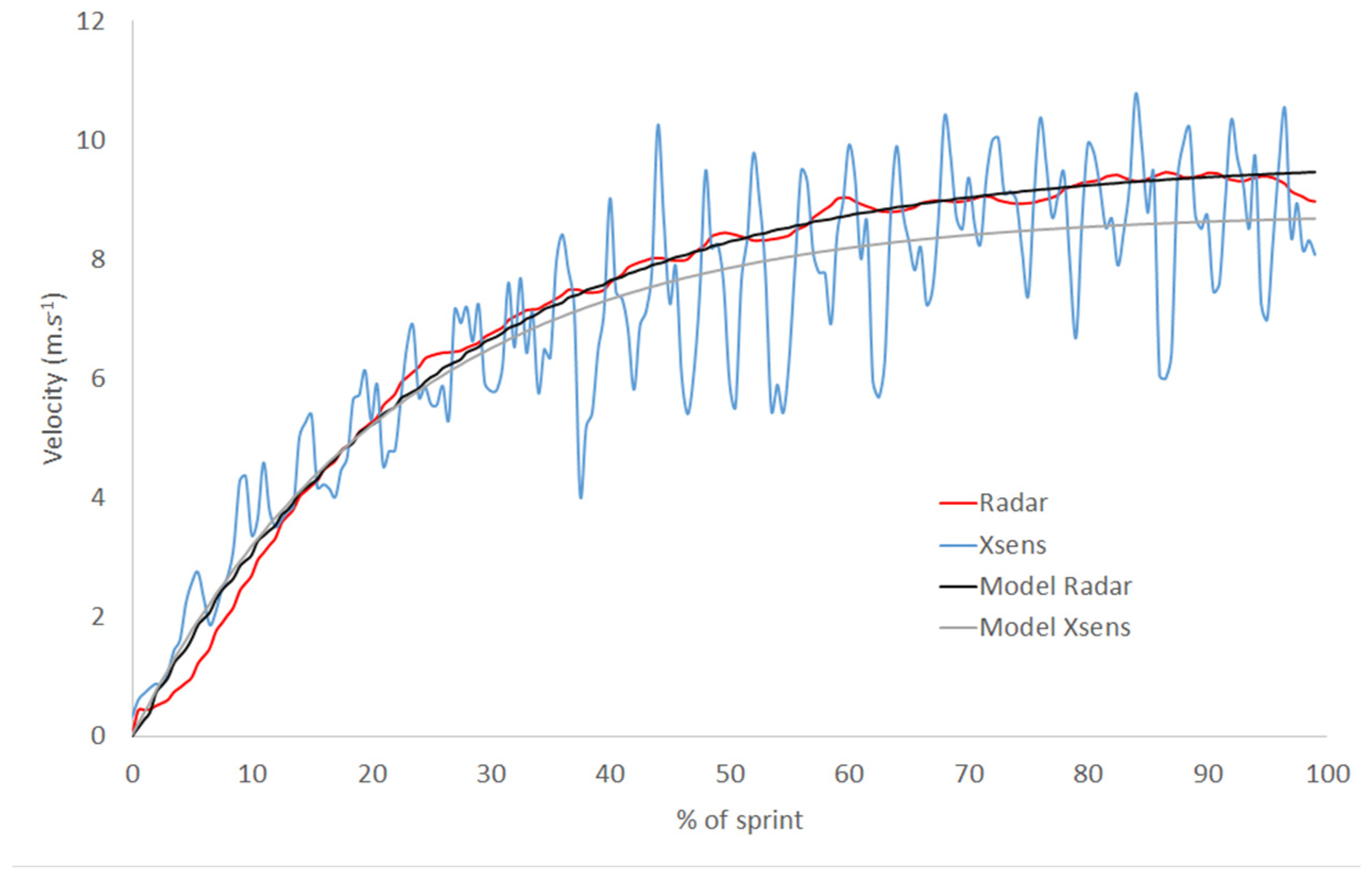
| Mean Radar (±SD) | Mean IMS (±SD) | Wilcoxon | Spearman | |
|---|---|---|---|---|
| (m·s−1) | 8.42 ± 1.11 | 7.96 ± 0.80 | 0.13 | r = 0.97; p ≤ 0.001 |
| τ (s) | 1.26 ± 0.12 | 1.18 ± 0.11 | 0.45 | r = 0.35; p = 0.44 |
| Mean Radar (±SD) | Mean IMS (±SD) | Wilcoxon | Spearman | |
|---|---|---|---|---|
| (m·s−1) | 8.42 ± 1.11 | 7.94 ± 0.80 | 0.13 | r = 0.97; p ≤ 0.001 |
| (N) | 381.5 ± 50.0 | 387.0 ± 54.1 | 0.61 | r = 0.81; p = 0.03 |
| (N/ m·s−1) | −45.5 ± 4.4 | −48.7 ± 4.5 | 0.45 | r = 0.31; p = 0.5 |
| (W) | 811.5 ± 183.8 | 780.1 ± 168.1 | 0.45 | r = 0.96; p ≤ 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slawinski, J.; Millot, B.; Houel, N.; Dinu, D. Use of an Inertial Measurement System to Calculate Maximal Power during Running Sprint Acceleration: Comparison with the Radar System. Proceedings 2020, 49, 23. https://doi.org/10.3390/proceedings2020049023
Slawinski J, Millot B, Houel N, Dinu D. Use of an Inertial Measurement System to Calculate Maximal Power during Running Sprint Acceleration: Comparison with the Radar System. Proceedings. 2020; 49(1):23. https://doi.org/10.3390/proceedings2020049023
Chicago/Turabian StyleSlawinski, Jean, Benjamin Millot, Nicolas Houel, and Daniel Dinu. 2020. "Use of an Inertial Measurement System to Calculate Maximal Power during Running Sprint Acceleration: Comparison with the Radar System" Proceedings 49, no. 1: 23. https://doi.org/10.3390/proceedings2020049023
APA StyleSlawinski, J., Millot, B., Houel, N., & Dinu, D. (2020). Use of an Inertial Measurement System to Calculate Maximal Power during Running Sprint Acceleration: Comparison with the Radar System. Proceedings, 49(1), 23. https://doi.org/10.3390/proceedings2020049023





