Wood Bat Durability as a Function of Bat Profile and Slope of Grain †
Abstract
:1. Introduction
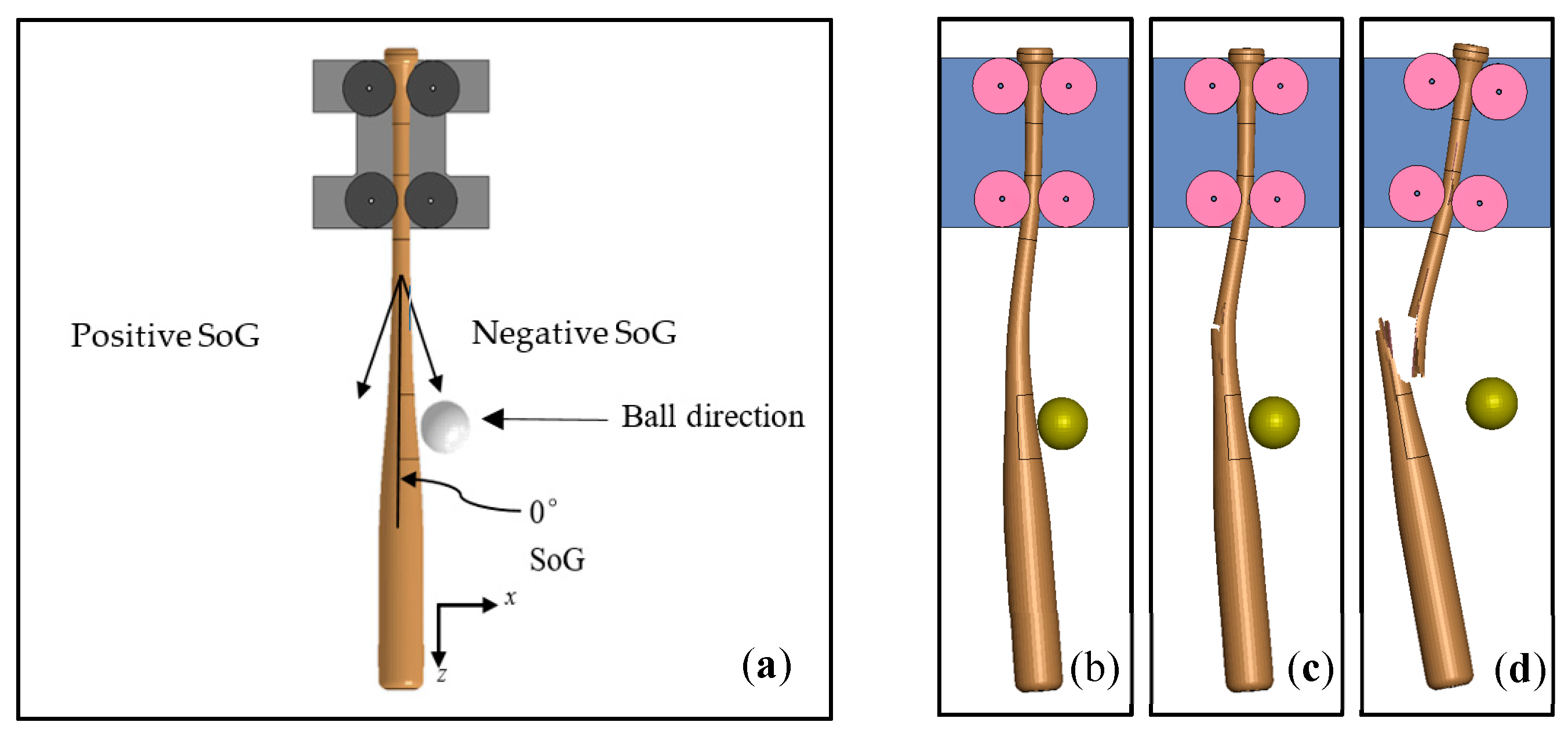
2. Methodology
2.1. Bat Profiles
2.2. Finite Element Modeling
2.3. Wood Failure Criteria
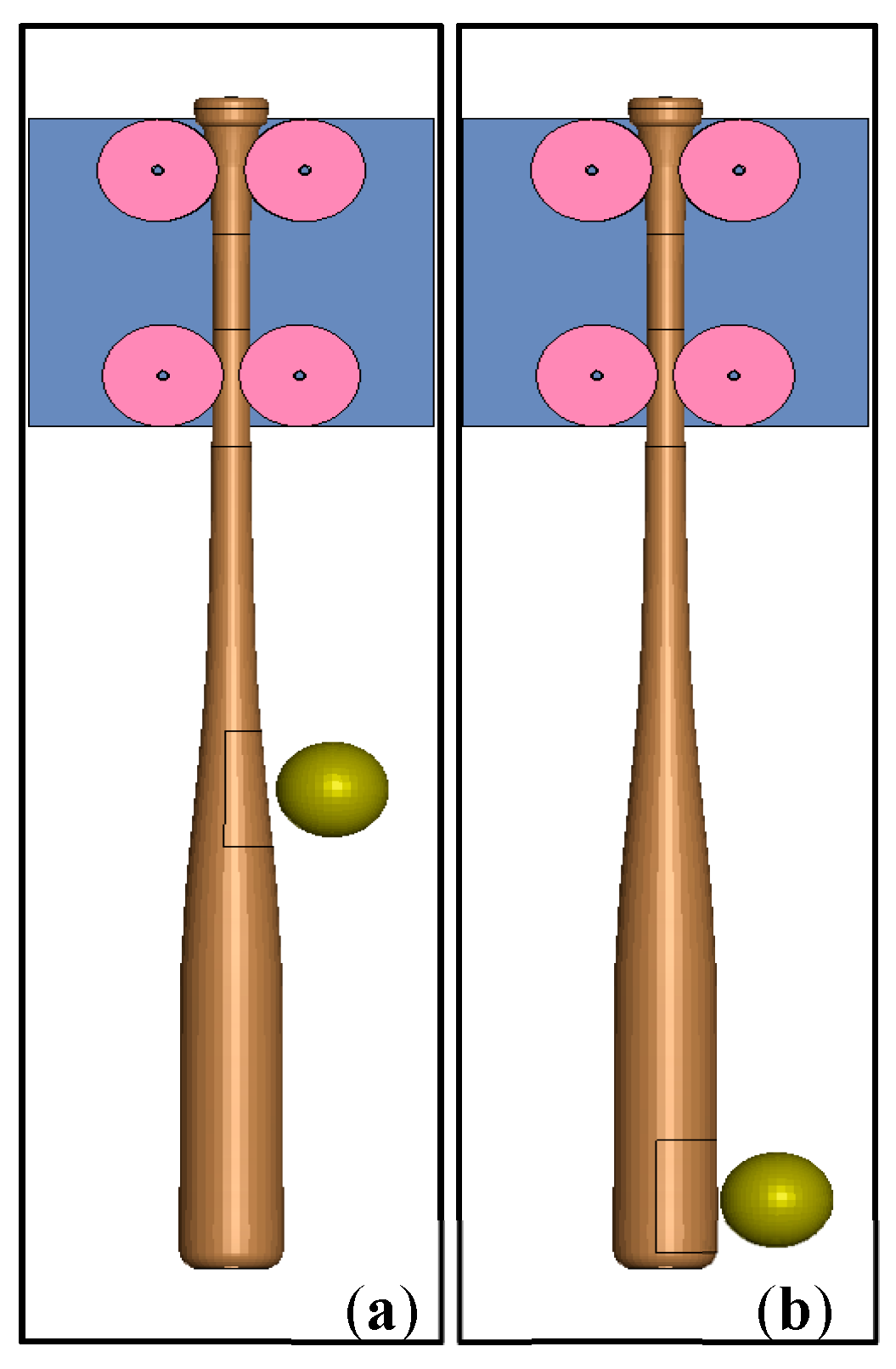
2.4. Dynamic Impacts
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Major League Baseball. Major League Baseball 2009 Bat Supplier Regulations. The Office of the Commissioner of Baseball, 15 December 2008. [Google Scholar]
- Major League Baseball. Major League Baseball 2010 Bat Supplier Regulations. The Office of the Commissioner of Baseball, 6 January 2010. [Google Scholar]
- Major League Baseball. Agreement Regarding Players’ Use of Approved Bats in Major League Games for the 2010 Season. The Office of the Commissioner of Baseball, 7 January 2010. [Google Scholar]
- Major League Baseball. Major League Baseball 2011 Bat Supplier Regulations. The Office of the Commissioner of Baseball, 2011. [Google Scholar]
- Major League Baseball. Major League Baseball 2012 Bat Supplier Regulations. The Office of the Commissioner of Baseball, December 2012. [Google Scholar]
- Saraceno, J. Taking Swing at Safer Bats, Man Says His Creation Curbs Exploding Effect. USA TODAY, 15 August 2016; FA CHASE EDITION P.1C. [Google Scholar]
- Fortin-Smith, J.; Sherwood, J.; Drane, P.; Ruggiero, E.; Campshure, B.; Kretschmann, D. A Finite Element Investigation into the Effect of Slope of Grain on Wood Baseball Bat Durability. Appl. Sci. 2019, 9, 3733. [Google Scholar] [CrossRef]
- Fortin-Smith, J.; Sherwood, J.; Drane, P.; Kretschmann, D. Characterization of Maple and Ash Material Properties for the Finite Element Modeling of Wood Baseball Bats. Appl. Sci. 2018, 8, 2256. [Google Scholar] [CrossRef]


| Bat Profile | Profile Image |
|---|---|
| A |  |
| B |  |
| C |  |
| Profile ID | Min. Handle Diameter (in. [cm]) | 12 in. (30.5 cm) Location (in. [cm]) | 16.5 in. (41.9 cm) Location (in. [cm]) | 18 in. (45.7 cm) Location (in. [cm]) | 21 in. (53.3 cm) Location (in. [cm]) | Max. Barrel Diameter (in. [cm]) |
|---|---|---|---|---|---|---|
| A | 0.909 [2.322] | 1.022 [2.596] | 1.268 [3.221] | 1.440 [3.658] | 1.942 [4.933] | 2.594 [6.589] |
| B | 0.931 [2.309] | 1.041 [2.644] | 1.303 [3.310] | 1.466 [3.724] | 1.945 [4.940] | 2.587 [6.571] |
| C | 0.914 [2.365] | 1.049 [2.664] | 1.323 [3.360] | 1.457 [3.701] | 1.850 [4.699] | 2.501 [6.353] |
| Profile | Volume (in3 [cm3]) | Density (lb/in3 [g/cm3]) | Strain-to-Failure | ||
|---|---|---|---|---|---|
| A | 88.66 | [1453] | 0.0218 | [0.603] | 0.0212 |
| B | 84.24 | [1380] | 0.0230 | [0.637] | 0.0223 |
| C | 79.68 | [1306] | 0.0243 | [0.673] | 0.0234 |
| Bat Profile | 14.0 in (35.6 cm) Impact | 2.0 in (5.1 cm) Impact | ||
|---|---|---|---|---|
| Speed (mph [km/h]) | SoG (deg.) | Speed (mph [km/h]) | SoG (deg.) | |
| A | 135 [217] | 2 | 130 [209] | 0 |
| B | 120 [193] | 2 | 125 [201] | 0 |
| C | 130 [209] | 2 | 140 [225] | 0 |
| Bat Profile | 14.0 in (35.6 cm) Impact | 2.0 in (5.1 cm) Impact | ||
|---|---|---|---|---|
| Speed (mph [km/h]) | SoG (deg.) | Speed (mph [km/h]) | SoG (deg.) | |
| A | 155 [249] | 0 | 180 [290] | −1 |
| B | 160 [257] | 0 | 175 [282] | −1 |
| C | 160 [257] | 0 | 160 [258] | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campshure, B.; Drane, P.; Sherwood, J. Wood Bat Durability as a Function of Bat Profile and Slope of Grain. Proceedings 2020, 49, 97. https://doi.org/10.3390/proceedings2020049097
Campshure B, Drane P, Sherwood J. Wood Bat Durability as a Function of Bat Profile and Slope of Grain. Proceedings. 2020; 49(1):97. https://doi.org/10.3390/proceedings2020049097
Chicago/Turabian StyleCampshure, Blake, Patrick Drane, and James Sherwood. 2020. "Wood Bat Durability as a Function of Bat Profile and Slope of Grain" Proceedings 49, no. 1: 97. https://doi.org/10.3390/proceedings2020049097
APA StyleCampshure, B., Drane, P., & Sherwood, J. (2020). Wood Bat Durability as a Function of Bat Profile and Slope of Grain. Proceedings, 49(1), 97. https://doi.org/10.3390/proceedings2020049097





