Fine Electrolytic Tough Pitch Copper Multistage Wiredrawing Pass Schedule Design by Analytical and Numerical Methods †
Abstract
1. Introduction
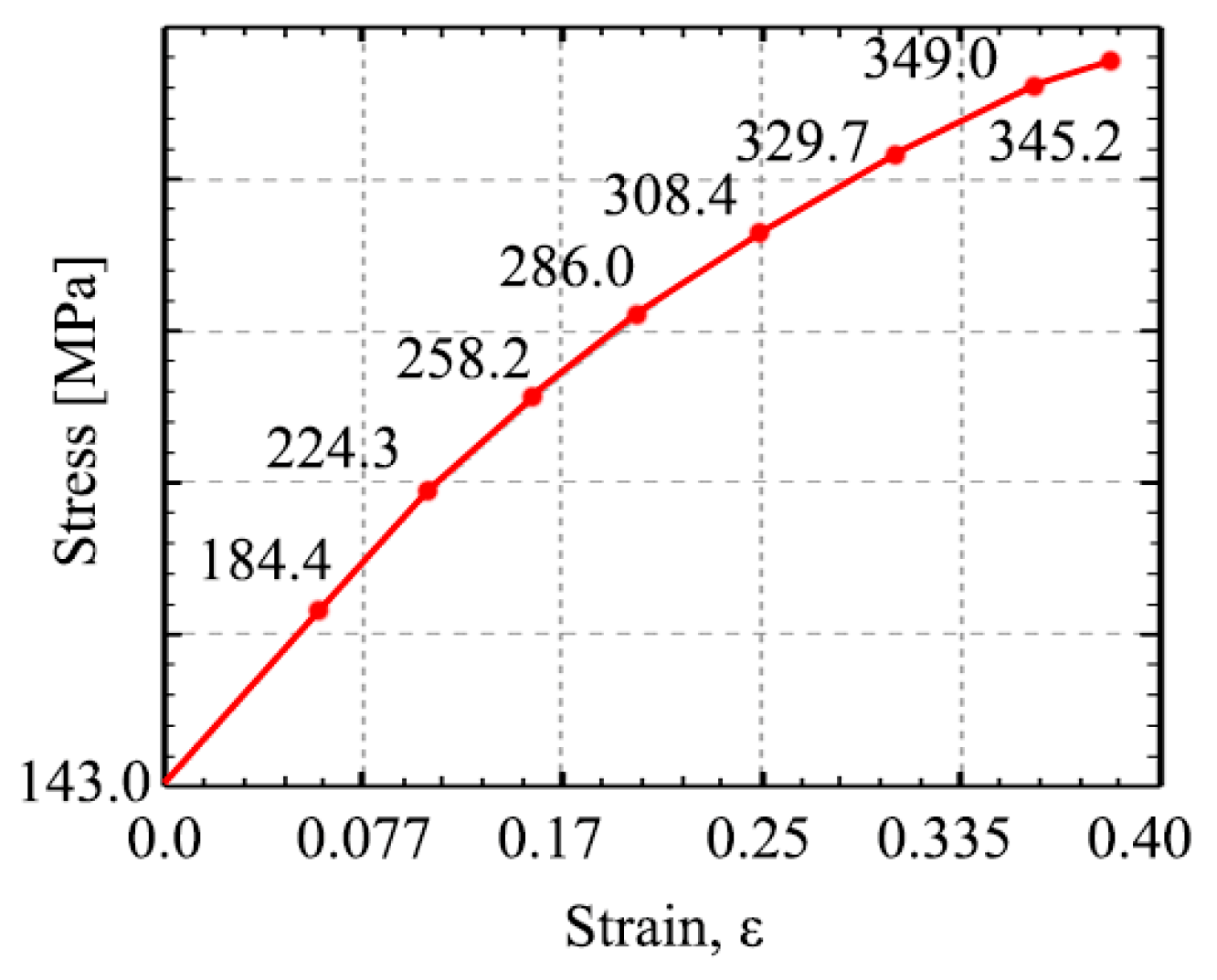
2. Materials and Methods
3. Results
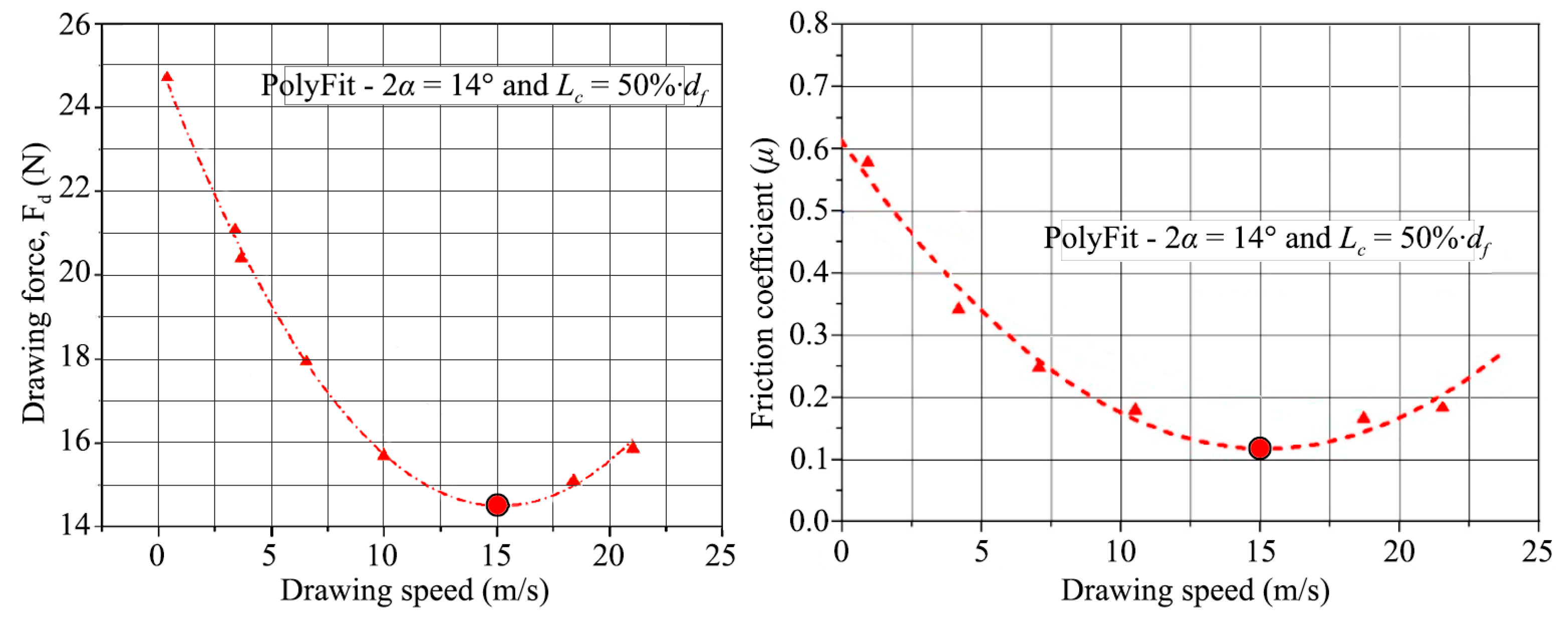
3.1. Experimental Determination of the Friction Coefficient
3.2. Analytical Definition of the Multi-Step Pass Schedule Design by PullWorks Software
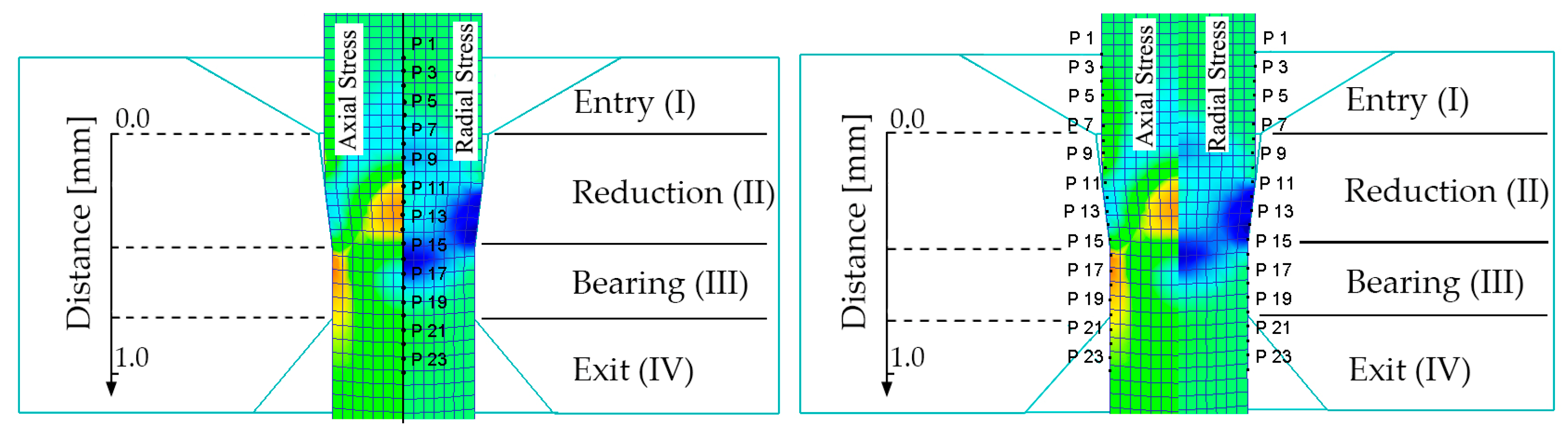
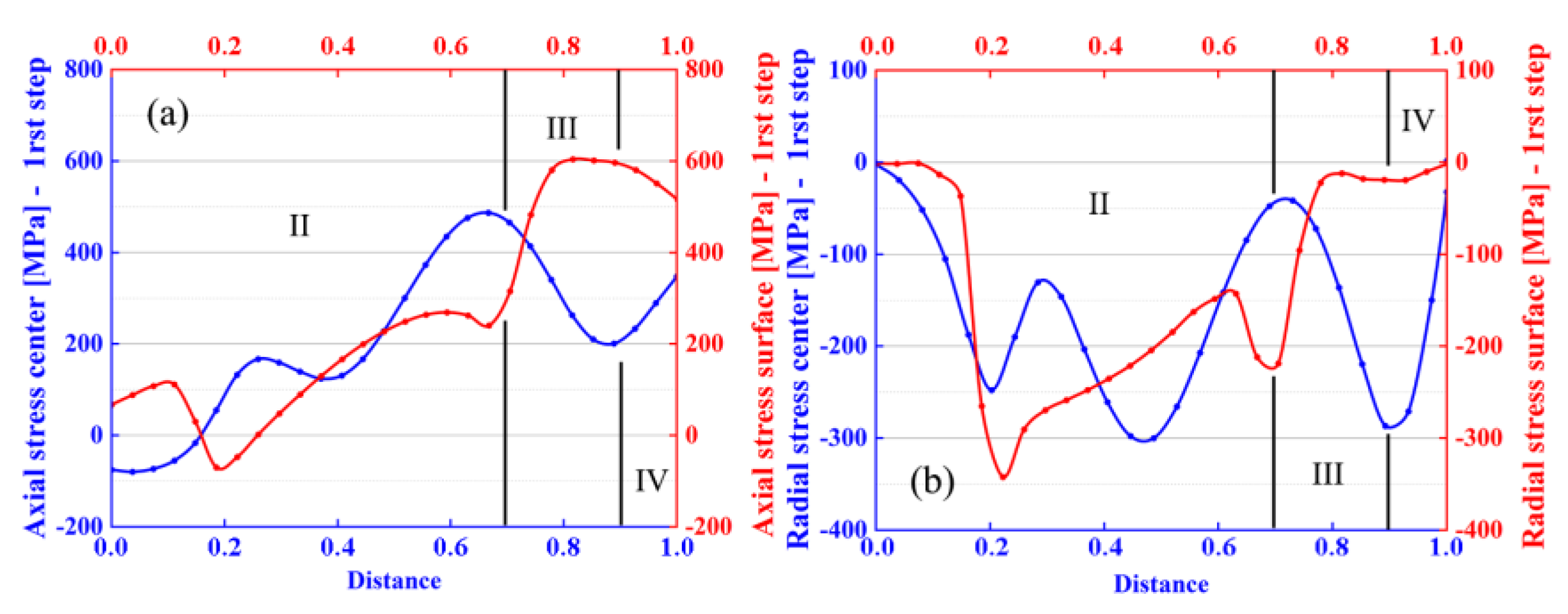
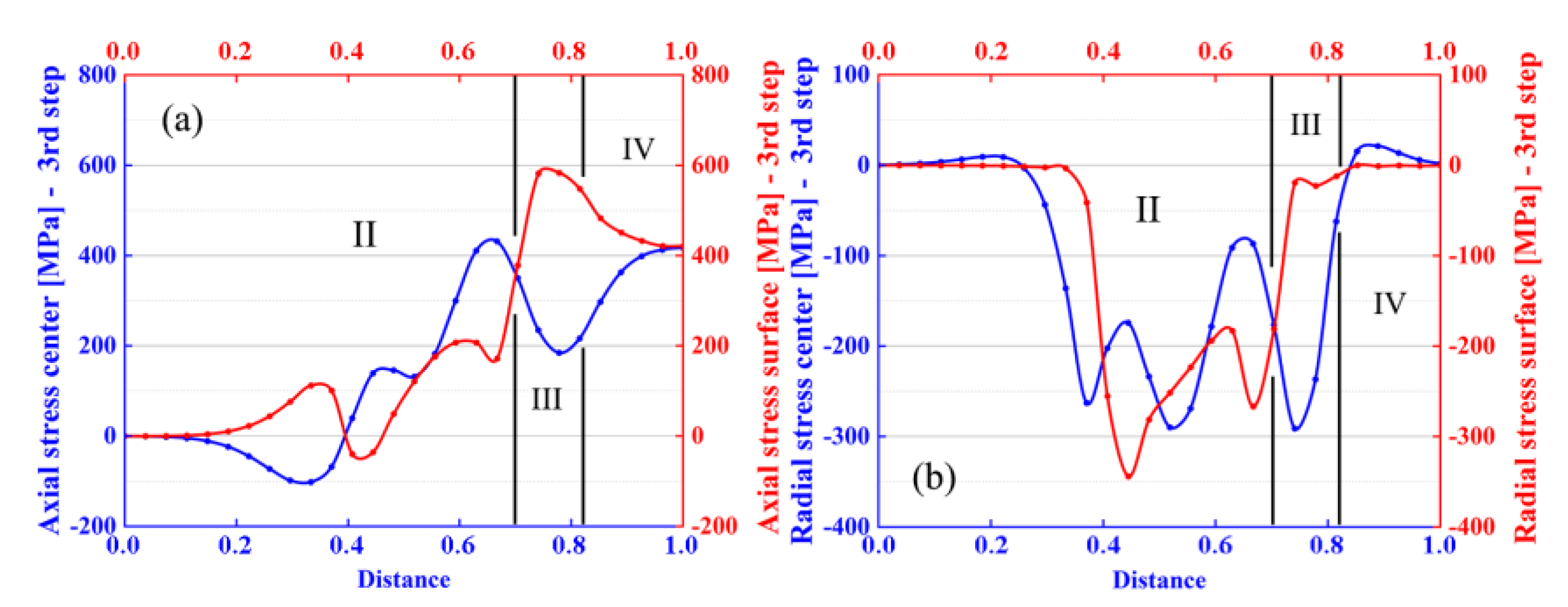
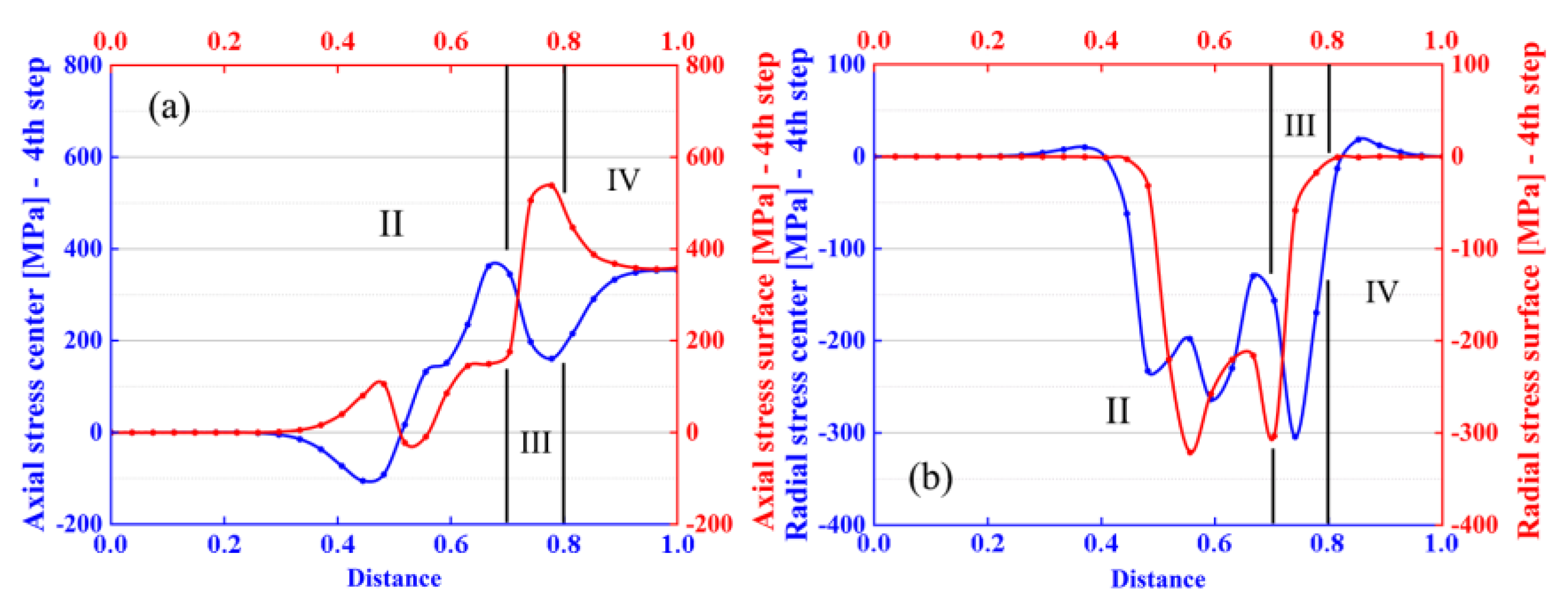
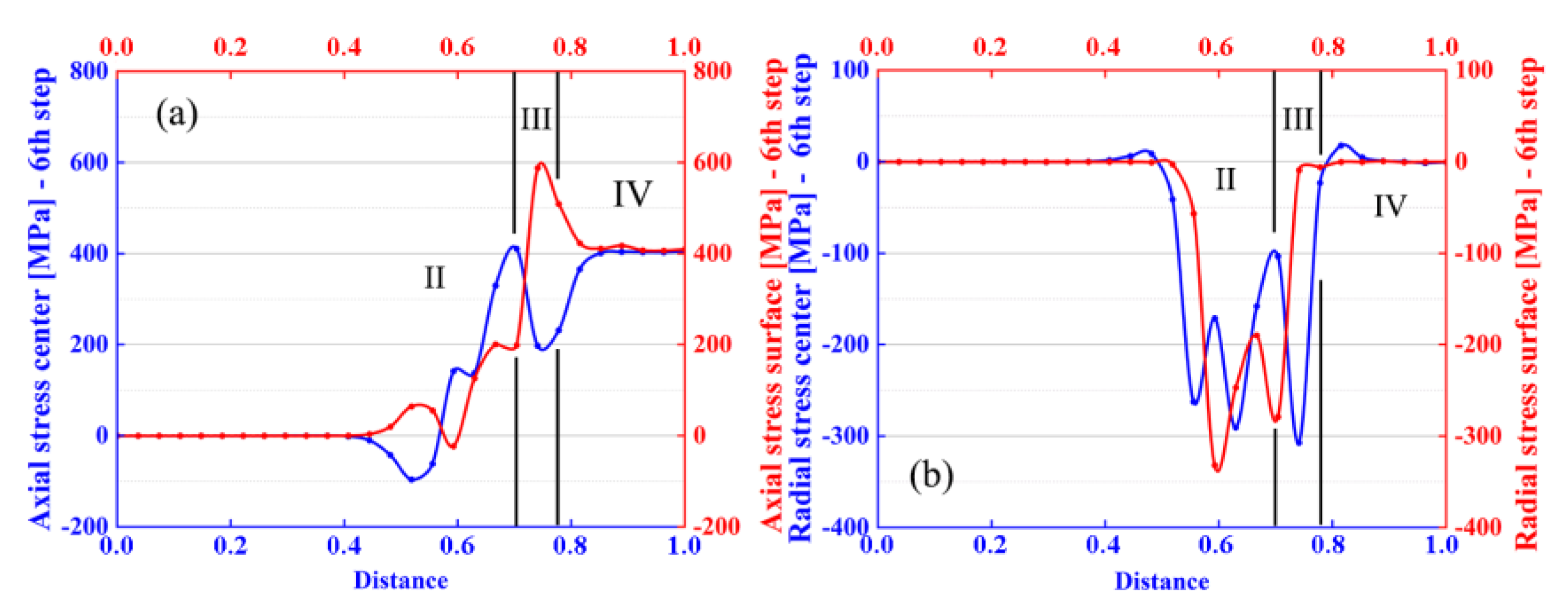
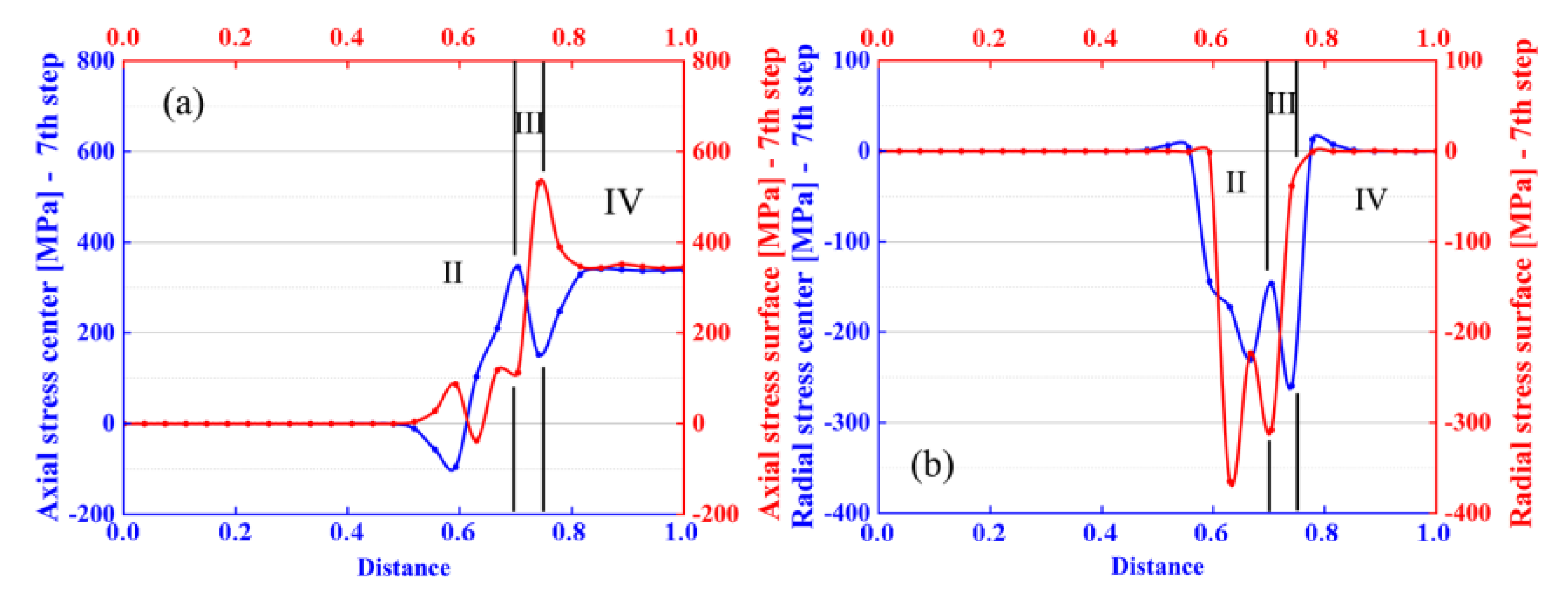
3.3. Numerical FEM Study of the Proposed Multi-Step Pass Schedule
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parnian, P.; Parsa, M.H.; Mirzadeh, H.; Jafarian, H.R. Effect of Drawing Strain on Development of Martensitic Transformation and Mechanical Properties in AISI 304L Stainless Steel Wire. Steel Res. Int. 2017, 88, 1–10. [Google Scholar] [CrossRef]
- Son, S.B.; Lee, Y.K.; Kang, S.H.; Chung, H.S.; Cho, J.S.; Moon, J.T.; Oh, K.H. A numerical approach on the inclusion effects in ultrafine gold wire drawing process. Eng. Fail. Anal. 2011, 18, 1272–1278. [Google Scholar] [CrossRef]
- Kustra, P.; Milenin, A.; Byrska-Wójcik, D.; Grydin, O.; Schaper, M. The process of ultra-fine wire drawing for magnesium alloy with the guaranteed restoration of ductility between passes. J. Mater. Process. Technol. 2017, 247, 234–242. [Google Scholar] [CrossRef]
- Schade, P. Wire drawing failures and tungsten fracture phenomena. Int. J. Refract. Met. Hard Mater. 2006, 24, 332–337. [Google Scholar] [CrossRef]
- Lee, S.-K.; Lee, I.-K.; Lee, S.-Y.; Hwang, S.-K. Fabrication of 50.0 µm Ultra-Fine Pure Rhodium Wire, Using a Multi-Pass Wire Drawing Process, for Probe Card Pins. Materials 2019, 12, 2194. [Google Scholar] [CrossRef]
- Martinez, G.A.S.; Qian, W.-L.; Kabayama, L.K.; Prisco, U. Effect of Process Parameters in Copper—Wire Drawing. Metals 2020, 10, 105. [Google Scholar] [CrossRef]
- Pops, H. The Metallurgy of Copper Wire. Copper Development Association Inc. 1997. Available online: https://www.copper.org/publications/newsletters/innovations/1997/12/wiremetallurgy.html (accessed on 9 December 2020).
- Vega, G.; Haddi, A.; Imad, A. Investigation of process parameters effect on the copper-wire drawing. Mater. Des. 2009, 18, 3308–3312. [Google Scholar] [CrossRef]
- Kabayama, L.K.; Taguchi, S.P.; Martinez, G.A.S. The Influence of Die Geometry on Stress Distribution by Experimental and FEM Simulation on Electrolytic Copper Wiredrawing. Mater. Res. 2009, 12, 281–285. [Google Scholar] [CrossRef]
- Adamczyk, J.; Suliga, M.; Pilarczyk, J.; Burdek, M. The Influence of Die Approach and Bearing Part of Die on Mechanical-Technological Properties of High Carbon Steel Wires. Arch. Metall. Mater. 2012, 57, 12–14. [Google Scholar] [CrossRef]
- Rubio, E.M.; Camacho, A.M.; Sevilla, L.; Sebastián, M.A.; Sevilla, L. Calculation of the forward tension in drawing processes. J. Mater. Process. Technol. 2005, 162, 551–557. [Google Scholar] [CrossRef]
- Rubio, E.M. Analytical methods application to the study of tube drawing processes with fixed conical inner plug: Slab and Upper Bound Methods. J. Achiev. Mater. Manuf. Eng. 2006, 14, 119–130. [Google Scholar]
- Rodriguez-Alabanda, O.; Romero, P.E.; Guerrero-Vaca, G.; Sevilla, L. Software implementation of a new analytical methodology applied to the multi-stage wire drawing process: The case study of the copper wire manufacturing line optimization. Int. J. Adv. Manuf. Technol. 2018, 96, 2077–2089. [Google Scholar] [CrossRef]
- Hassan, A.K.F.; Hashim, A.S. Three Dimensional Finite Element Analysis of Wire Drawing Process. Univers. J. Mech. Eng. 2015, 3, 71–82. [Google Scholar] [CrossRef]
- Rodriguez-Alabanda, O. PullWorks Software Application for the Analytical Study and Optimization of the Wiredrawing Process. Available online: https://youtu.be/jawQDkiYvek (accessed on 9 December 2020).
- Avitzur, B. Analysis of Wire Drawing and Extrusion through Conical Dies of Large Cone Angle. J. Eng. Ind. 1964, 86, 305. [Google Scholar] [CrossRef]
- Avitzur, B. Handbook of Metal Forming; John Wiley & Sons Inc.: New York, NY, USA, 1983. [Google Scholar]
- Bitkov, V.V. Minimization of breaks during drawing thin wire of nonferrous metals. Russ. J. Non-Ferrous Met. 2010, 51, 134–139. [Google Scholar] [CrossRef]
- Evans, W.; Avitzur, B. Measurement of Friction in Drawing, Extrusion, and Rolling. J. Lubr. Technol. 1968, 90, 72–80. [Google Scholar] [CrossRef]
- Kovács, S.; Mertinger, V. Examination of Complex Optimization Objective Functions of Parameters of Multi- Step Wire Drawing Technology. Acta Polytecnica Hung. 2013, 10, 27–44. [Google Scholar]
- Narayanan, K.R.; Sridhar, I.; Subbiah, S. Effect of cold work on the mechanical response of drawn ultra-fine gold wire. Comput. Mater. Sci. 2010, 49 (Suppl. S1), S119–S125. [Google Scholar] [CrossRef]
- Naga Teja, C.S.; Murty N, G.; Reddy Teja, P.S. Finite Element Analysis of Wire Drawing Process with different die contours. Int. J. Sci. Eng. Adv. Technol. 2016, 4, 134–143. [Google Scholar]
- Sas-Boca, I.M.; Tintelecan, M.; Pop, M.; Iluţiu-Varvara, D.-A.; Mihu, A.M. The Wire Drawing Process Simulation and the Optimization of Geometry Dies. Procedia Eng. 2017, 181, 187–192. [Google Scholar] [CrossRef]
- Zottis, J.; Diehl, C.A.T.S.; Rocha, A.D.S. Evaluation of experimentally observed asymmetric distributions of hardness, strain and residual stress in cold drawn bars by FEM-simulation. J. Mater. Res. Technol. 2018, 7, 469–478. [Google Scholar] [CrossRef]
- Esteves Group Hileras de Diamante Policristalino PCD. Available online: http://www.estevesgroup.com/es/products/wire-drawing-dies/polycrystalline-dies (accessed on 9 December 2020).
- Rodriguez-Alabanda, O. PullWorks Software. Available online: http://www.uco.es/grupos/prinia/oscar-rodriguez-alabanda (accessed on 9 December 2020).
- Wright, R.N. Mechanical analysis and die design. Wire J. Int. 1979, 12, 60–61. [Google Scholar]
- Fluhrer, J. Deform2D Version 8.1 User´s Manual; Scientific Forming Technologies Corp.: Columbus, OH, USA, 2004. [Google Scholar]
- Cheng, H.S. Lubrication Regimes, ASM Handbook Vol.18, Friction, Lubrication, and Wear Technology; ASM International: West Conshohocken, PA, USA, 1992. [Google Scholar]
- Martinez Santana, G.A.; Ferro dos Santos, E.; Kabayama, L.K.; Siqueira Guidi, E.; de Azebedo Silva, F. Influences of Different Die Bearing Geometries on the. Metals 2019, 9, 1089. [Google Scholar] [CrossRef]






| Step Nr. | Input, d0(i) [mm] | Output, df(i) [mm] | Reduction Ratio, r | Unit Strain, ε | Shape Factor, Δ | Continuous Annealing |
|---|---|---|---|---|---|---|
| 1 | 0.50 | 0.39 | 0.40 | 0.50 | 1 | YES |
| 2 | 0.39 | 0.31 | 0.40 | 0.46 | 1 | YES |
| 3 | 0.31 | 0.24 | 0.40 | 0.51 | 1 | YES |
| 4 | 0.24 | 0.19 | 0.40 | 0.47 | 1 | YES |
| 5 | 0.19 | 0.15 | 0.40 | 0.47 | 1 | YES |
| 6 | 0.15 | 0.12 | 0.40 | 0.45 | 1 | YES |
| 7 | 0.12 | 0.10 | 0.31 | 0.36 | 1.34 | YES |
| Step Nr. | Drawing Force, Fd (PullWorks) [N] | Drawing Force, Fd (FEM) [N] | Drawing Stress, σd (PullWorks) [MPa] | Drawing Stress, σd (FEM) [MPa] |
|---|---|---|---|---|
| 1 | 45.9 | 53.2 | 384.5 | 445.3 |
| 2 | 27 | 30.1 | 357.2 | 398.8 |
| 3 | 17.9 | 19.4 | 394.4 | 428.8 |
| 4 | 10.3 | 10.7 | 363 | 377.4 |
| 5 | 6.5 | 7.3 | 366.9 | 413.1 |
| 6 | 3.9 | 4.5 | 348.7 | 397.9 |
| 7 | 2.5 | 2.6 | 321 | 331 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Alabanda, O.; Molero, E.; Tintelecan, M.; Guerrero-Vaca, G.; Romero, P.E.; Santana Martinez, G.A. Fine Electrolytic Tough Pitch Copper Multistage Wiredrawing Pass Schedule Design by Analytical and Numerical Methods. Proceedings 2020, 63, 12. https://doi.org/10.3390/proceedings2020063012
Rodríguez-Alabanda O, Molero E, Tintelecan M, Guerrero-Vaca G, Romero PE, Santana Martinez GA. Fine Electrolytic Tough Pitch Copper Multistage Wiredrawing Pass Schedule Design by Analytical and Numerical Methods. Proceedings. 2020; 63(1):12. https://doi.org/10.3390/proceedings2020063012
Chicago/Turabian StyleRodríguez-Alabanda, Oscar, Esther Molero, Marius Tintelecan, Guillermo Guerrero-Vaca, Pablo E. Romero, and Gustavo Aristides Santana Martinez. 2020. "Fine Electrolytic Tough Pitch Copper Multistage Wiredrawing Pass Schedule Design by Analytical and Numerical Methods" Proceedings 63, no. 1: 12. https://doi.org/10.3390/proceedings2020063012
APA StyleRodríguez-Alabanda, O., Molero, E., Tintelecan, M., Guerrero-Vaca, G., Romero, P. E., & Santana Martinez, G. A. (2020). Fine Electrolytic Tough Pitch Copper Multistage Wiredrawing Pass Schedule Design by Analytical and Numerical Methods. Proceedings, 63(1), 12. https://doi.org/10.3390/proceedings2020063012






