Abstract
This work presents a method for extracting parameters from photovoltaic (PV) solar cells, based on the three critical points of the current-voltage (I-V) characteristic, i.e., the short-circuit current, the open circuit voltage and the maximum power point (MPP). The method is developed in the Python programming language using differential evolution (DE) and a three-point curve fitting approach. It shows a good precision with root mean square error (RMSE), for different solar cells, lower than to those cited in the literature. In addition, the method is tested based on the measurements of a solar cell in the Faculty of Science and Technology of Tangier (FSTT) laboratory, thus giving a good agreement between the measured data and those calculated (i.e., RMSE = 7.26 × 10−4) with fewer iterations for convergence.
1. Introduction
In recent decades, access to renewable energy (RE) sources has attracted a lot of attention. In fact, growing concerns over the environmental situation and the energy crisis due to the limited quantities of fossil fuel reserves have made the development and adoption of RE an urgent priority. The PV option has proven to be a leader among many promising renewable technologies to replace fossil fuels due to lower PV technology prices and improved efficiency of solar cells thus leading to a significant growth in the PV industry [1,2,3]. PV are mainly divided into three technologies; poly-crystalline, mono-crystalline and thin films. Since these technologies rely mostly on the PV effect in silicon P-N junctions, their behavior can be modeled using electric diode circuits [4,5]. These circuits include different components where each is representative of a certain physical mechanism within the cell such as exciton recombination and cell bulk resistance. Knowing the exact values of these parameters is important for many applications. The simulation and emulation of PV cells is crucial for energy yield prediction, quality control during manufacturing [2] and the study of PV cell degradation. However, the values of these parameters are not available in the manufacturers’ technical data sheets. Open-circuit voltage, short-circuit current, and maximum power are given only under standard test conditions (STC). Obviously, the actual PV modules operation is generally far from these ideal conditions, which makes real-time fast parameter extraction necessary.
2. The Single Diode Model
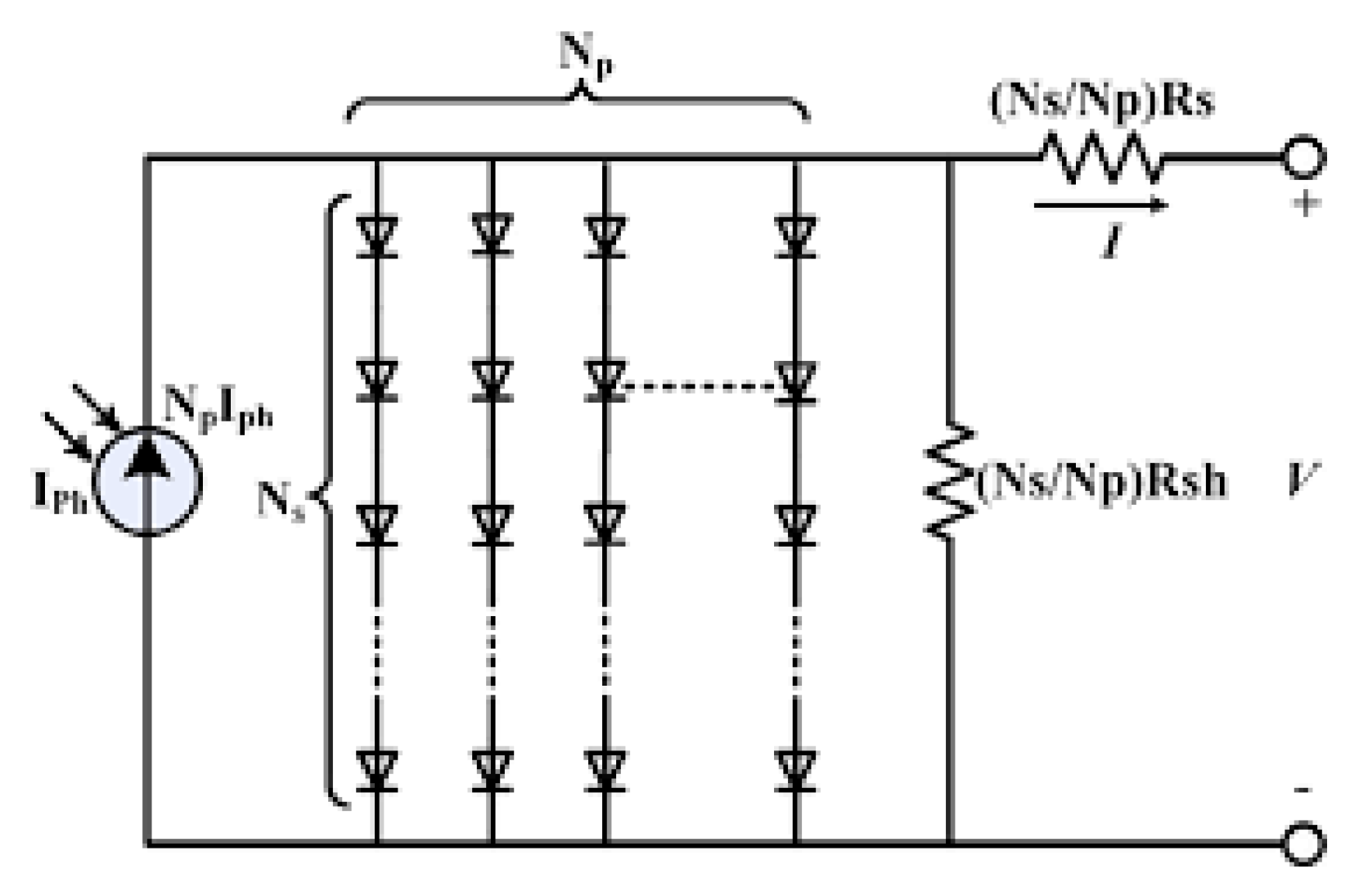
The simplest model used for PV solar cells is the single diode model (SDM) [6] as shown in Figure 1. The current generator represents the photocurrent (Iph) that is due to the PV effect, the diode represents the P-N junction and its electric field through the diode ideality factor (n) and the saturation current (I0), the series and shunt resistances (Rs and Rsh) represent cell bulk resistance and leakage current, respectively. The SDM is used for the three dominant technologies in the PV industry (namely, mono-Si, poly-Si and thin films), but for other emerging technologies which do not rely on the electric field of the P-N junction for exciton separation [7,8], other more specialized models are necessary. This model is described by the Shockley diode equation for a PV module with Ns cells in series and Np in parallel:
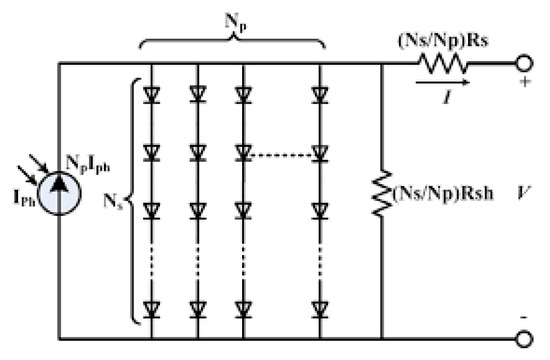
Figure 1.
Equivalent circuit SDM of PV module.
3. Background
For the parameters extraction of the model, one can distinguish two main strategies. Firstly, the analytical approach based on information from several key points on the I-V curve such as the short-circuit current (Isc), the open circuit voltage (Voc), the maximum power point (MPP) as well as the gradient of the curve at those points. This approach is simple and allows rapid calculations, however, several assumptions and simplifications can be made, thus leading to incorrect results [3,9,10]. This approach is also sensitive to measurement noise since it only relies on a few selected points [11].
The second strategy is the numerical approach, the problem of which is formulated as an optimization problem by trying to minimize the error between the calculated and measured values. This approach allows for the usage of the wide array of well-studied deterministic and stochastic optimization algorithms. The deterministic algorithms include methods such as the Newton Raphson method [12], Iterative curve-fitting [13], Conductivity method [14], Levenberg Marquardt algorithm [15], etc. These are gradient-based methods, which adds continuity, differentiability and convexity requirements on the error functions. In contrast, stochastic methods provide global search capability and do not require gradient information, meaning the error function can be non-differentiable, and even non-continuous, which include; the genetic algorithms (GA) [2,6,16], particle swarm optimization (PSO) [17,18], DE [1], artificial bee swarm optimization (ABSO) [19]. The issues encountered by these stochastic methods are mainly related to the vastness of the search spaces, which cost a lot of time to cover and require a few thousand iterations before converging. They can also be trapped in local minima but are much less susceptible to this problem when compared to their deterministic counterparts.
In this context, this work is based on the DE algorithm for the extraction of SDM parameters, namely Iph, I0, a, Rs and Rsh. The extraction method used is based on the three critical points (Voc, Isc, Pmpp) of the I-V curve whose model is forced to pass through these cited points. Furthermore, the method has been developed and implemented in the Python programming language, thus giving more precision and the need for few iterations for convergence.
4. The Proposed Method
The DE algorithm application to the SDM would result in a five-dimensional search space. In this work, three points of the I-V characteristic are used to analytically calculate three of the parameters whose search space is reduced to two dimensions. The ideality factor (a) and the series resistance (Rs) are the two parameters introduced into DE algorithm.
4.1. Differential Evolution
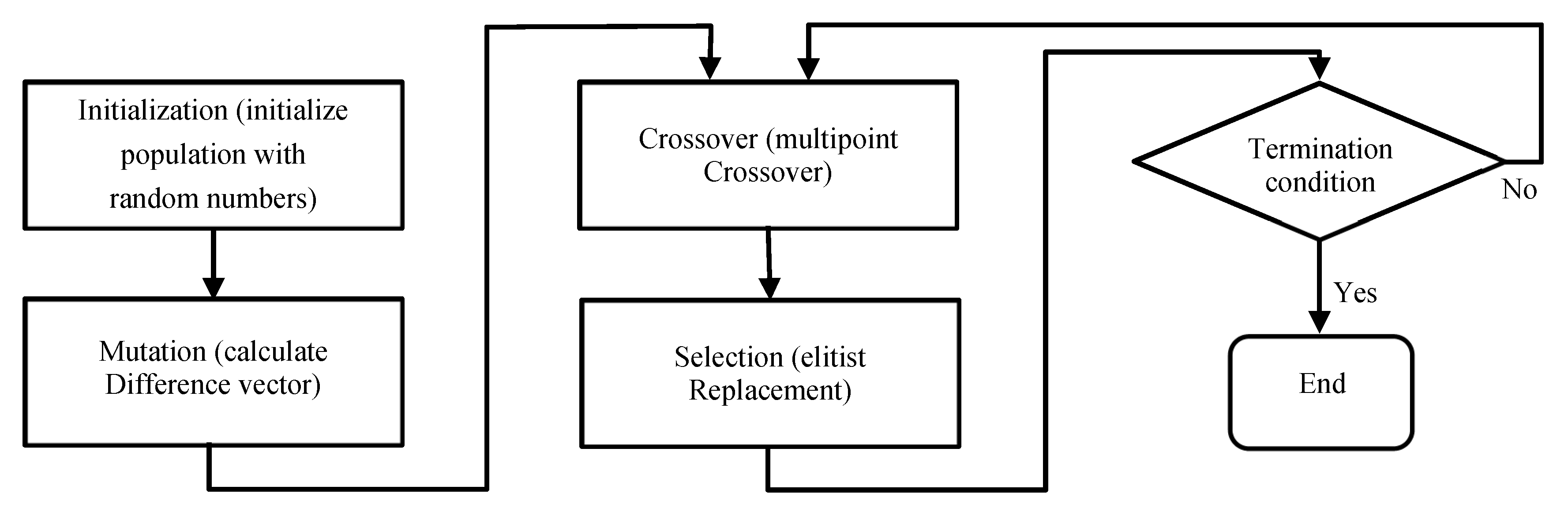
The DE introduced by Storn and Price in 1995 [20] is a relatively recent stochastic and evolutionary algorithm. It is very similar to other evolutionary algorithms like GA in that it also has crossing and mutation operations as shown in Figure 2.
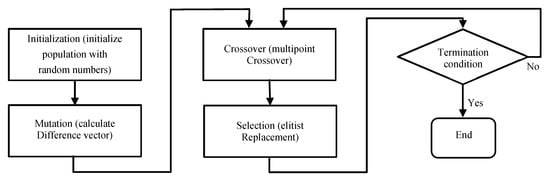
Figure 2.
Main operations of DE algorithm.
4.1.1. Initialization
First, we generate the initial population randomly trying to cover the entire search space. We may achieve this using Formula (2) assuming the rand (0, 1) term provides a uniform distribution of outputs.
The initial population is spread uniformly over the entire search space, which helps the algorithm avoid being stuck in local minima. DE is very efficient, which means the algorithm converges well within Genmax = 100 iterations, even with a small population NP = 50. The DE strategy is “DE/best/bin” which means that we choose the fittest vector in a population to generate mutants for the next generation, and that binomial crossover is performed on the trial vectors.
4.1.2. Mutation
Next, we create a mutant vector by taking the fittest vector in the population and adding the difference of two other random vectors from the population. The difference is scaled with a mutation factor F ∈ [0, 1]. This the key step that differentiates DE from other evolutionary methods according to the following formula:
4.1.3. Crossover
In this step, we created a trial vector by crossing over the elements from the mutant vector into the original. The probability of crossing over each element is set by the crossover rate, and we usually take high values (CR = 0.8) in order to promote diversity in the population [21]. A trial vector is generated as follows:
4.1.4. Penalty
One issue with DE is that unphysical values of the parameters can be obtained (i.e., negative Rs). To circumvent this, we apply a penalty to any unphysical solution by assigning it a large fitness value.
4.1.5. Selection
The last step is to select the vector based on whether or not its fitness value is superior to its previous generation counterpart. A possible method to achieve this is:
Note that, when the fitness function J is calculated, it evaluates to 100 for unphysical values as per the penalty phase. Storn and Price (2006) [21] recommend high crossover (CR = 0.7) and mutation factor (F ≥ 0.4) values. The limits used to penalize solution vectors are a ∈ [1, 2], Rs ∈ [0, 0.5] as well as the previously stated negative values of currents and resistances. We should note that the method is very sensitive to the choice of the MPP; then, the proposed method includes different running the algorithm times each with a slightly different MPP.
4.2. Three-Point Curve Fitting
In order to minimize the complexity of the algorithm, it is possible to reduce the dimensionality of the problem using a few geometrically critical points in the I-V curve, namely the short-circuit, open-circuit and maximum power regions. These three points will allow us to determine three SDM parameters:
Using algebraic manipulation, one can extract the three parameters Iph, Rsh, and I0:
where
and
Using this technique, the differential algorithm is executed in a two-dimensional search space, which considerably reduces the algorithm complexity.
5. Results and Discussion
5.1. The Schutten Solar STP6–120/36 Module
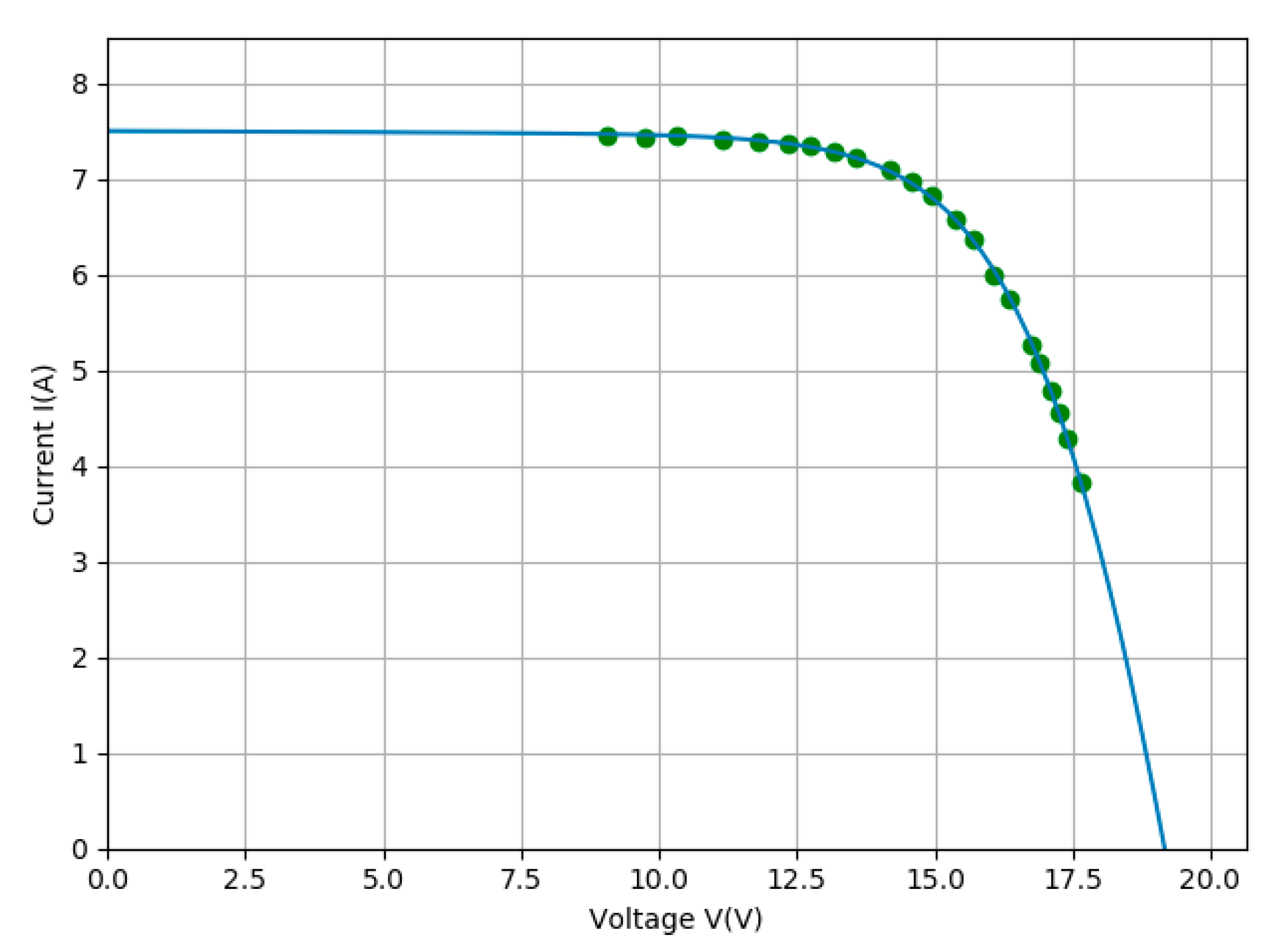
First, our code developed in Python gives a set of 22 data points of the I-V characteristic of the Schutten Solar STP6–120 module, which contains 36 solar cells, connected in series at a temperature of 55 °C. A comparison between the experimental dataset and the computed I-V curve is illustrated in Figure 3. We clearly see that the algorithm fits the dataset very well, despite most of the points being close the maximum power points and few being in the short-circuit and open-circuit regions. Table 1 compares the computed parameters using our code with those reported in [1].
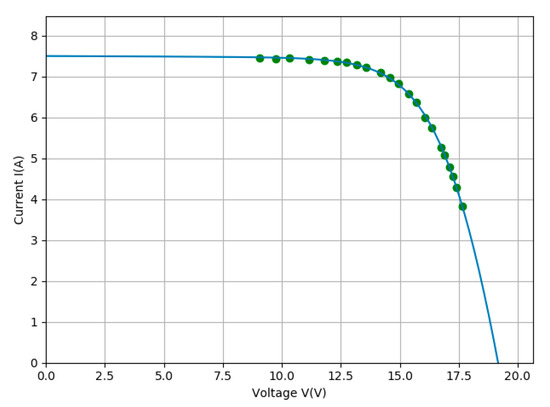
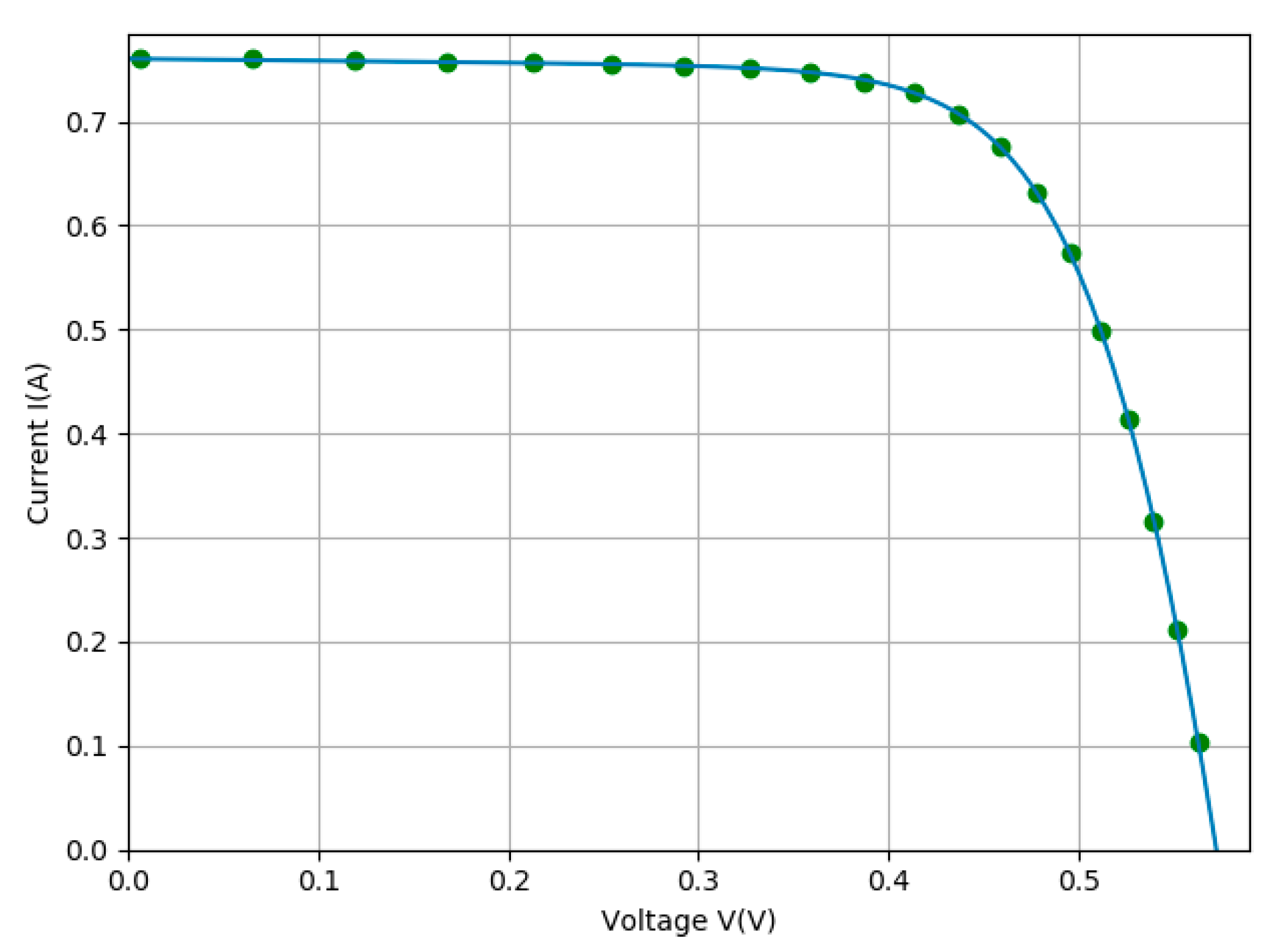
Figure 3.
A comparison between the experimental data (green dots) and the calculated characteristic (blue line) for the Schutten Solar STP6–120/36 module.

Table 1.
Parameter extraction results of the Schutten Solar STP6–120/36 module with those reported in [1].
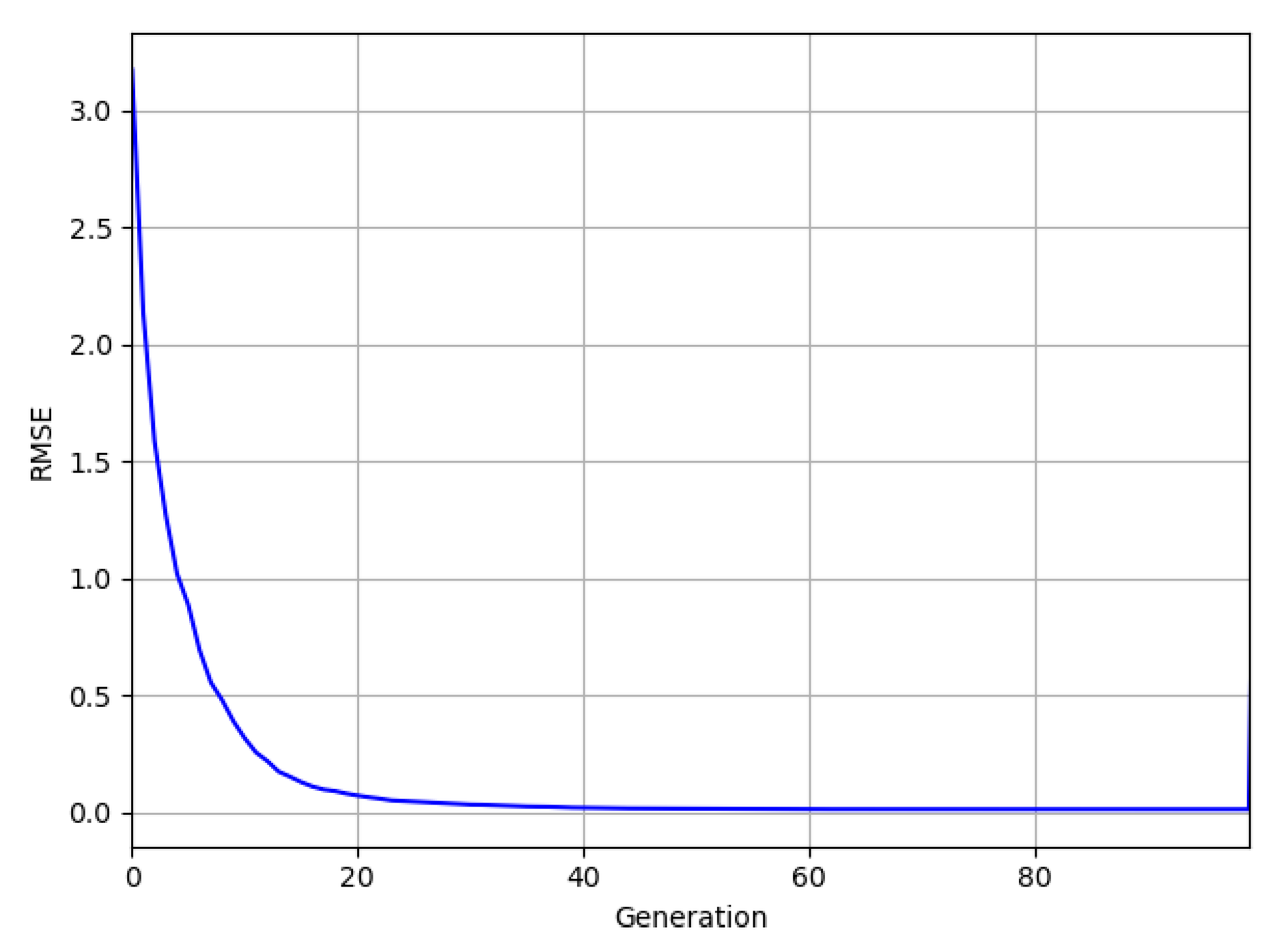
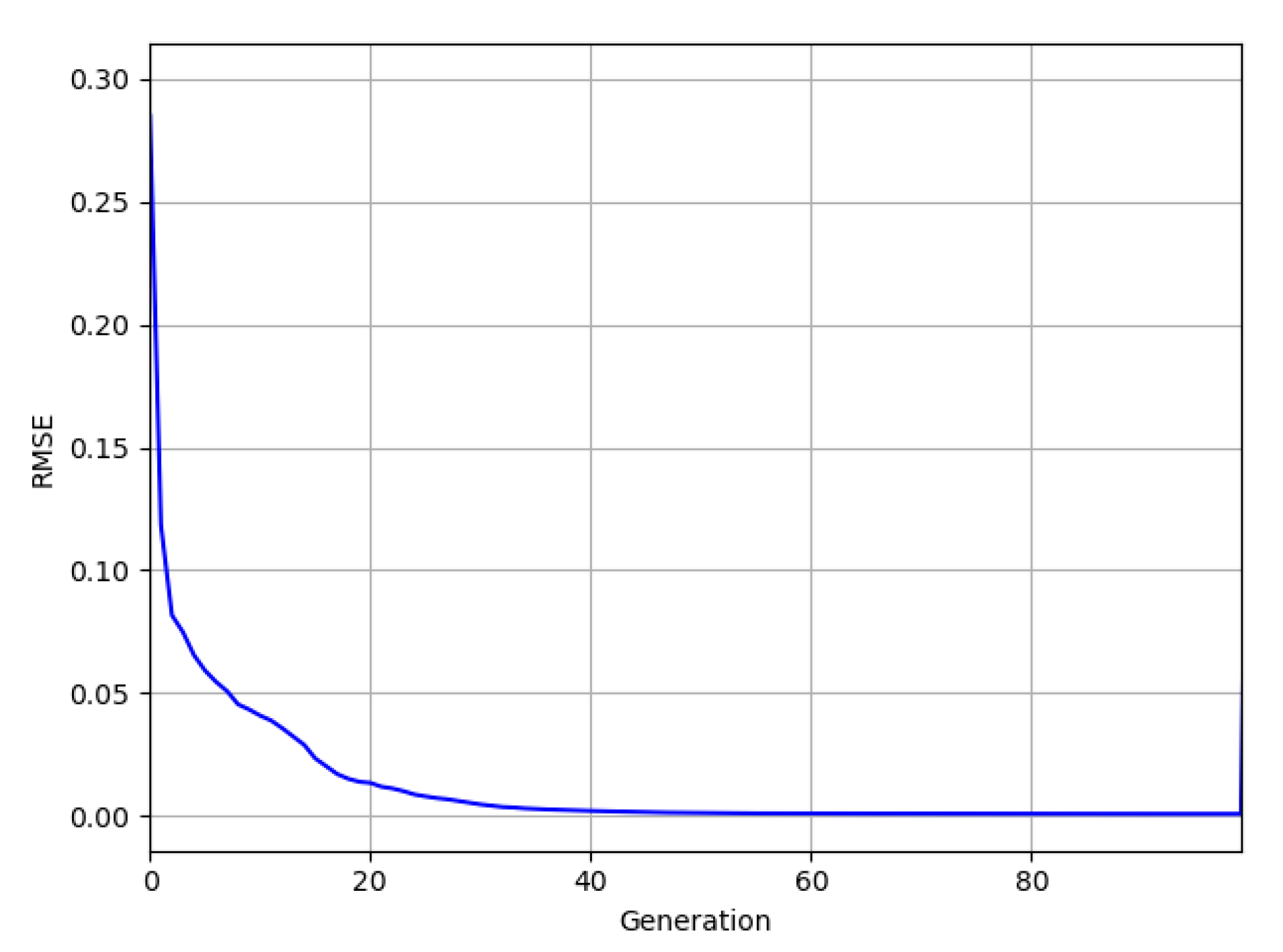
The fitness of a population is calculated by averaging each solution vector’s fitness in a specific generation. Its evolution is shown in Figure 4 where rapid convergence (within 30 iterations) is noticed towards the final value.
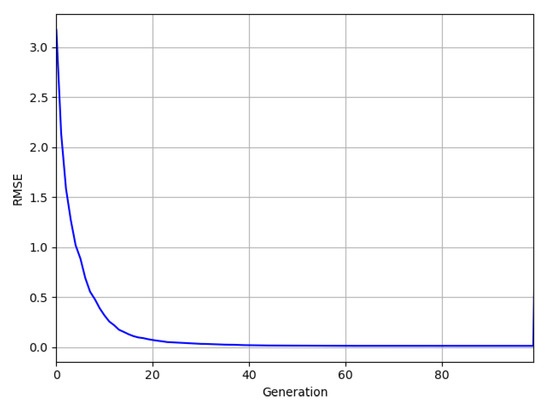
Figure 4.
The evolution of average population fitness throughout the 100 iterations.
5.2. The R.T.C. France Commercial Silicon Solar Cell
For this case, we study the R.T.C France commercial silicon solar cell. The experimental dataset was taken at a temperature of 33 °C. Subsequently, the method used manages to extract very precise parameter values (Figure 5). A comparison between the computed values python DE algorithm and the proposed method in [1] is shown in Table 2. We can see the DE algorithm is slightly more accurate, and this could be explained by the absence of the constraints that are introduced in [1] by utilizing the three pivot points. It turns out that by giving up some precision on the pivot points; we can slightly gain in overall accuracy.
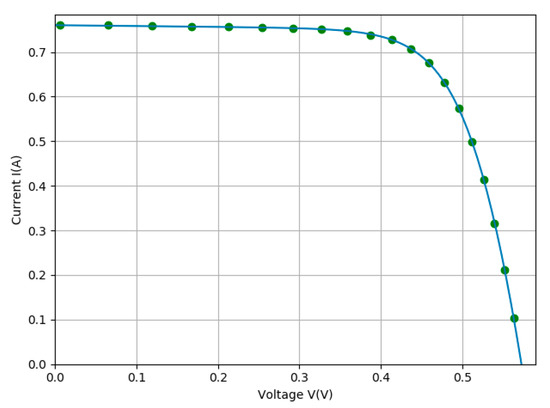
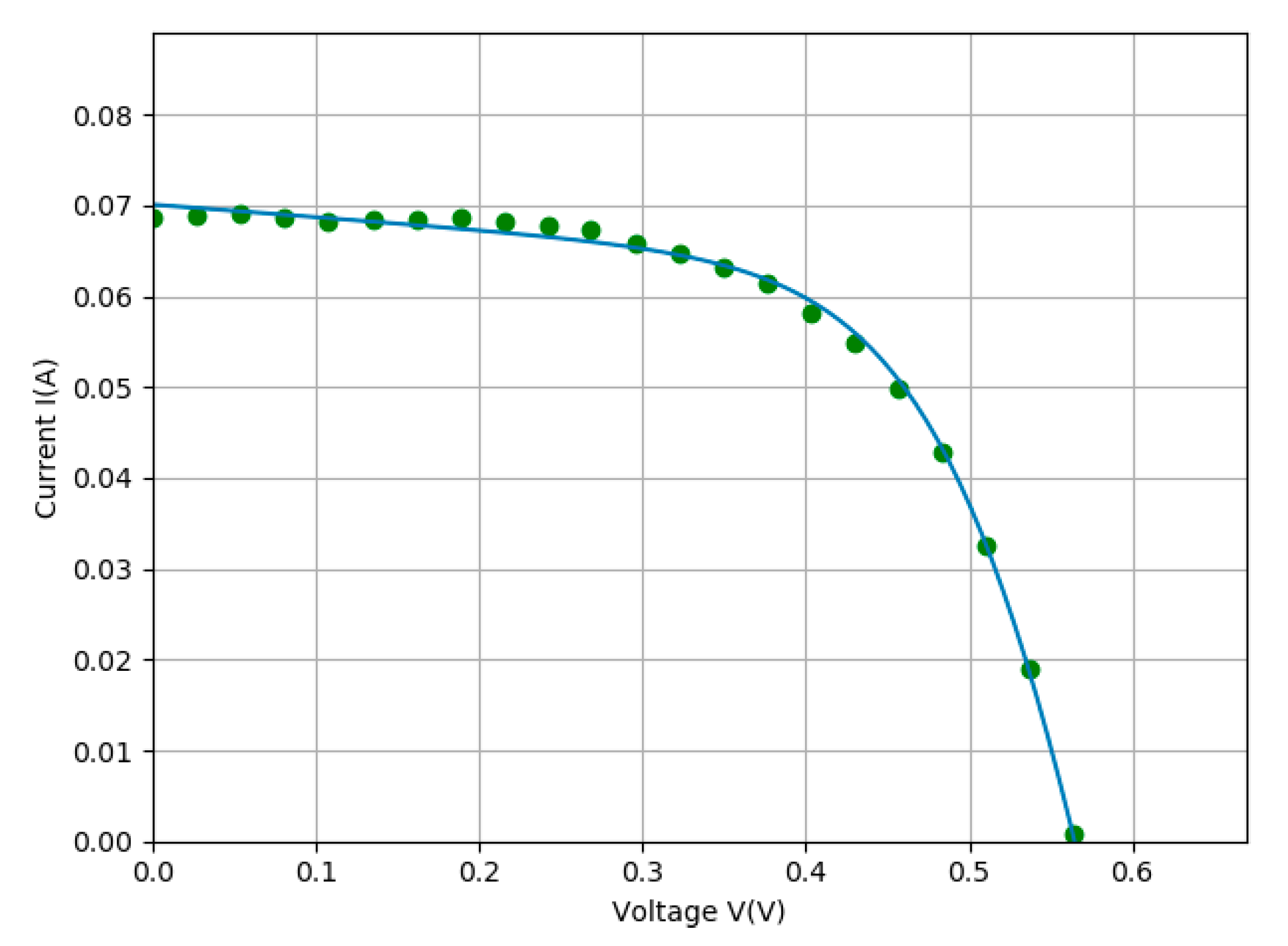
Figure 5.
Comparison between experimental data (green dots) and calculated I-V curve (blue line) for the R.T.C France solar cell.

Table 2.
Parameter extraction results of the R.T.C France commercial silicon solar cell with those reported in [1].
5.3. FSTT Laboratory Silicon Cell
In this section, we tested in our FSTT laboratory, using RaRe Solutions solar simulator, the proposed method of the DE algorithm to extract the parameters values of a solar cell at a temperature of 30 °C.
A comparison between experimental data and the computed I-V curve is shown in Figure 6. The parameter values corresponding to this solution are laid out in Table 3 and are associated with a RMSE of 7.26 × 10−4. The evolution of population fitness is shown in Figure 7.
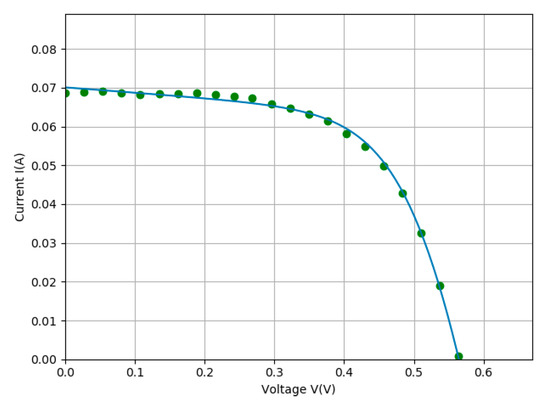
Figure 6.
Comparison between experimental data (green dots) and the algorithm calculated I–V curve (blue line) for the FSTT solar cell.

Table 3.
Extracted single diode parameter values for the FSTT cell.
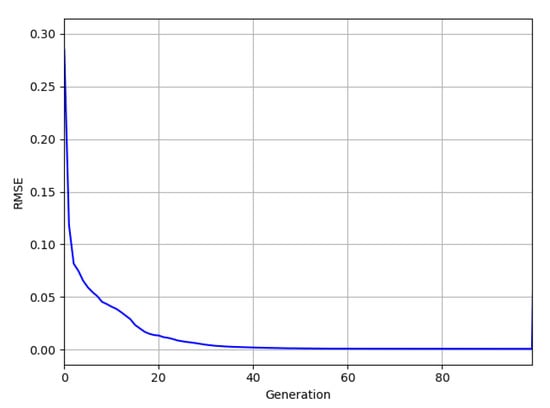
Figure 7.
Evolution of average population fitness in the 100 iterations.
6. Conclusions
This work represents a developed method of extracting SDM parameters from PV solar cells using DE and the three-point curve fitting approach. The method is implemented in Python requires very few iterations for convergence and giving more precision compared to the results cited in the literature. Furthermore, the Python code developed gives very consistent results on several executions. However, the method seems very sensitive to choice of MPP in the experimental dataset, which makes it necessary to perform several executions, each with a different choice of MPP. It should be noted that the use of the three points seems to slightly reduce the method precision. Whereas a naive DE scheme implies a five-dimensional research space and requires a few hundred iterations, which is slightly higher in precision terms. This can probably be explained by the noise measurement in the pivot points constraining the proposed method.
Author Contributions
Conceptualization, R.H. and Y.K.; methodology, R.H. and Y.K.; software, R.H. and Y.K.; validation, A.C., K.A., A.K., Y.K. and R.H., formal analysis, R.H., Y.K., A.C., K.A. and A.K.; investigation, R.H. and Y.K.; writing—original draft preparation, R.H.; writing—review and editing; A.C., K.A. and A.K.; supervision, K.A., A.K. and A.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chin, V.J.; Salam, Z. A New Three-point-based Approach for the Parameter Extraction of Photovoltaic Cells. Appl. Energy 2019, 237, 519–533. [Google Scholar] [CrossRef]
- Sellami, A.; Bouaïcha, A. Application of the Genetic Algorithms for Identifying the Electrical Parameters of PV Solar Generators. In Solar Cells-Silicon Wafer-Based Technologies; Kosyachenko, L.A., Ed.; IntechOpen Limited: London, UK, 2011; ISBN 978-953-307-747-5. [Google Scholar]
- Chin, V.; Salam, Z.; Ishaque, K. An accurate and fast computational algorithm for the two-diode model of PV module based on a hybrid method. IEEE Trans. Ind. Electron. 2017, 64, 6212–6222. [Google Scholar] [CrossRef]
- Oliva, D.; Aziz, M.A.E.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. An accurate modelling of the two-diode model of PV module using a hybrid solution based on differential evolution. Energy Convers. Manag. 2016, 124, 42–50. [Google Scholar] [CrossRef]
- Zagrouba, M.; Sellami, A.; Bouaïcha, M.; Ksouri, M. Identification of PV solar cells and modules parameters using the genetic algorithms: Application to maximum power extraction. Sol. Energy 2010, 84, 860–866. [Google Scholar] [CrossRef]
- Jiang, C.-S.; Yang, M.; Zhou, Y.; To, B.; Nanayakkara, S.U.; Luther, J.M.; Zhou, W.; Berry, J.J.; van de Lagemaat, J.; Padture, N.P.; et al. Carrier separation and transport in perovskite solar cells studied by nanometre-scale profiling of electrical potential. Nat. Commun. 2015, 6, 8397. [Google Scholar] [CrossRef] [PubMed]
- Scharber, M.; Sariciftci, N.S. Efficiency of bulk-heterojunction organic solar cells. Prog. Polym. Sci. 2013, 38, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Ishaque, K.; Salam, Z.; Mekhilef, S.; Shamsudin, A. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution. Appl. Energy 2012, 99, 297–308. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H.; Shamsudin, A. A critical evaluation of EA computational methods for photovoltaic cell parameter extraction based on two-diode. Sol. Energy 2011, 85, 1768–1779. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear Minimization Algorithm for Determining the Solar Cell Parameters with Microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Chan, D.S.H.; Phang, J.C.H. Analytical methods for the extraction of solar-cell single- and double-diode model parameters from I-V characteristics. IEEE Trans. Electron Devices 1987, 34, 286–293. [Google Scholar] [CrossRef]
- Chegaar, M.; Ouennoughi, Z.; Hoffmann, A. New method for evaluating illuminated solar cell pa- rameters. Solid-State Electron 2001, 45, 293–296. [Google Scholar] [CrossRef]
- Ikegami, T.; Maezono, T.; Nakanishi, F.; Yamagata, Y.; Ebihara, K. Estimation of equivalent circuit parameters of PV module and its application to optimal operation of PV system. Sol. Energy Mater. Sol. Cells 2001, 67, 389–395. [Google Scholar] [CrossRef]
- Jervase, J.A.; Bourdoucen, H.; Al-Lawati, A. Solar cell parameter extraction using genetic algorithms. Meas. Sci. Technol. 2001, 12, 1922–1925. [Google Scholar] [CrossRef]
- Sandrolini, L.; Artioli, M.; Reggiani, U. Numerical method for the extraction of photovoltaic module double-diode model parameters through cluster analysis. Appl. Energy 2010, 87, 442–451. [Google Scholar] [CrossRef]
- Soon, J.; Low, K.; Member, S. Photovoltaic Model Identification Using Particle Swarm Optimization with Inverse Barrier Constraint. IEEE Trans. Power Electron. 2012, 27, 3975–3983. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 2013, 102, 943–949. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report TR-95–012; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin, Germany, 2005. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).