The Effects of Weighting Functions on the Performances of Robust Control Systems ^†

Abstract

An important stage in robust control design is to define the desired performances of the closed loop control system using the models of the frequency sensitivity functions S. If the frequency sensitivity functions remain within the limits imposed by these models, the control performances are met. In terms of the sensitivity functions, the specifications include: shape of S over selected frequency ranges, peak magnitude of S, bandwidth frequency, and tracking error at selected frequencies. In this context, this paper presents a study of the effects of the specifications of the weighting functions on the performances of robust control systems.

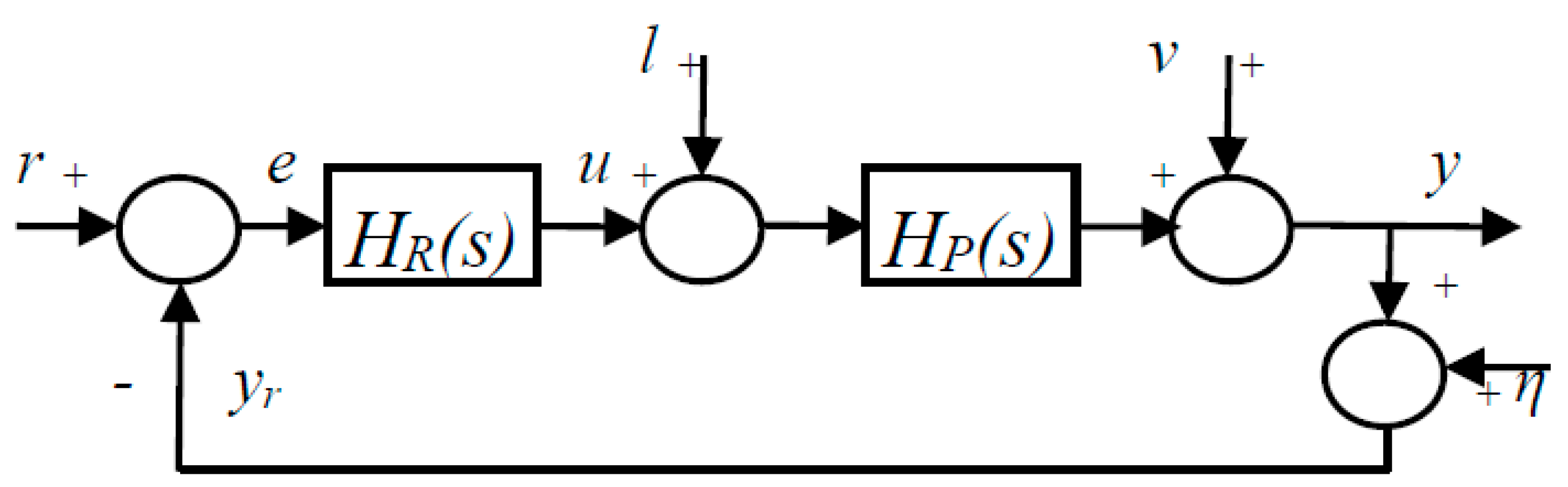
1. Introduction

In general, the design objectives of any control system are defined using different models which implement the desired responses to a specified reference. So, the closed-loop control system becomes stable, achieves the imposed performances, rejects the disturbances and measurement noise, and avoids the saturation of actuators, even in the presence of modeling uncertainties or change in the operating point [1,2,3,4,5].

In the H-infinity synthesis, the objectives refer to the optimization of the H-infinity norm of the closed-loop system, considering all the external input variables (references, disturbances, noises) and all the output variables according to the block diagram from Figure 1, where: $H_p\left(s\right)$ and $H_R\left(s\right)$ are the plant and controller transfer functions, $r$—reference input, $e$—control error, $y_r$—feedback signal, $y$—the plant output, $u$—control signal, $v,l$—disturbances, and $\eta$—measurement noise.

The input–output behavior of the system is characterized by the energy transfer from the external variables $r, v, \eta , l$ to the output variable $y$ (and sometime to the control variable u). Considering the relation $H_d\left(s\right)=H_R\left(s\right)H_p\left(s\right)$, there are four important transfer functions to fully describe the system:

• The sensitivity function $S\left(j\omega \right)={\left[1+H_d\left(j\omega \right)\right]}^{-1};$
• The complementary sensitivity function $T\left(j\omega \right)=H_d\left(j\omega \right)\cdot {\left[1+H_d\left(j\omega \right)\right]}^{-1}=H_d\left(j\omega \right)S\left(j\omega \right);$
• The noise sensitivity function $R_S\left(j\omega \right)=H_R\left(j\omega \right)\cdot {\left[1+H_d\left(j\omega \right)\right]}^{-1}=H_R\left(j\omega \right)S\left(j\omega \right);$
• The load sensitivity function $P_S\left(j\omega \right)=H_p\left(j\omega \right){\left[1+H_d\left(j\omega \right)\right]}^{-1}=H_p\left(j\omega \right)\cdot S\left(j\omega \right).$

If $l=0$, the relations between $y$ and $r, v, \eta$, respectively, between $e$ and $r, v, \eta$ are given by:

$$y=\frac{H_d\left(s\right)}{1+H_d\left(s\right)}\cdot r-\frac{H_d\left(s\right)}{1+H_d\left(s\right)}\cdot \eta +\frac{1}{1+H_d\left(s\right)}\cdot v=T\cdot r-T\cdot \eta +S\cdot v,$$

(1)

$$e=\frac{1}{1+H_d\left(s\right)}\cdot r-\frac{1}{1+H_d\left(s\right)}\cdot v+\frac{H_d\left(s\right)}{1+H_d\left(s\right)}\cdot \eta =S\cdot r-S\cdot v+T\cdot \eta$$

(2)

The sensitivity function S describes the input–output behavior from input $v$ to the output $y$, if the other input variables are $r=0, \eta =0, l=0$. In (1), if $\eta =0, T=1, S=0$, the reference tracking and disturbance rejection result.

In the block diagram from Figure 1, it is often necessary to include some weighting cost functions, chosen to reflect the design objectives and information about noise and disturbance [5]. The modified block diagram including these weighting functions is presented in Figure 2.

Although there are some recommendations for choosing the weighting functions, these depend on the designer skills and involves several iterations until a final form is achieved, which guarantees the control performances imposed to the closed loop system.

The paper [6] presents the robust analysis of a positioning control system where the weighting-functions-based tuning method simplifies the H-infinity design procedure. In [7], the μ-synthesis robust design method is used for a multi-model control problem. The selection of the weighting functions is made for low, medium and high frequencies. The studies from [8] presents the disadvantages of the H-infinity design method. At the same time, the authors had chosen the weighting functions for the μ-synthesis of a Proportional-Integrative (PI) controller, in order to improve the performances of the robust system.

A theoretical guide for choosing the weighting functions and the design procedure which assures the system gains are developed in the paper [1].

The paper [9] is focused on determining the weighting functions under two aspects: initial selection and tuning procedure which improves the performances of the closed-loop system. An interesting procedure for choosing the weighting functions for the optimal H-infinity design formulated as an optimization problem is presented in [10]. The paper [11] contains the synthesis issue for a nominal controller with unstable weighting functions. The authors proposed a simplification of the robust controller design procedure.

The papers [2,12,13] present some techniques for choosing the weighting functions, reducing the order of the transfer functions and designing the robust controllers using the Matlab Toolbox. Robust control methods are developed in [3,4] for both linear and nonlinear systems, and approaches of robust control theory based on weighting functions are also addressed in [5].

In [14], the authors proposed a weighting function modeling method which is used in H infinity loop-shaping design and tested in the numerical simulation. Other methodologies for selecting the sensitivity functions are shown in [15]. For multiple input multiple output (MIMO) systems, an application of choosing the reduced order weighting function is developed in [16].

The paper presents in Section 2 and Section 3 the models for choosing the weighting functions in accordance with the robust theory, a short analysis of two of these models (S and R_S) and the influence of some parameters (magnitude, bandwidth frequency, tracking error). Section 4 contains the analysis of the performances of the closed-loop control system which depend on the parameters of the weighting functions. The conclusions are highlighted in Section 5.

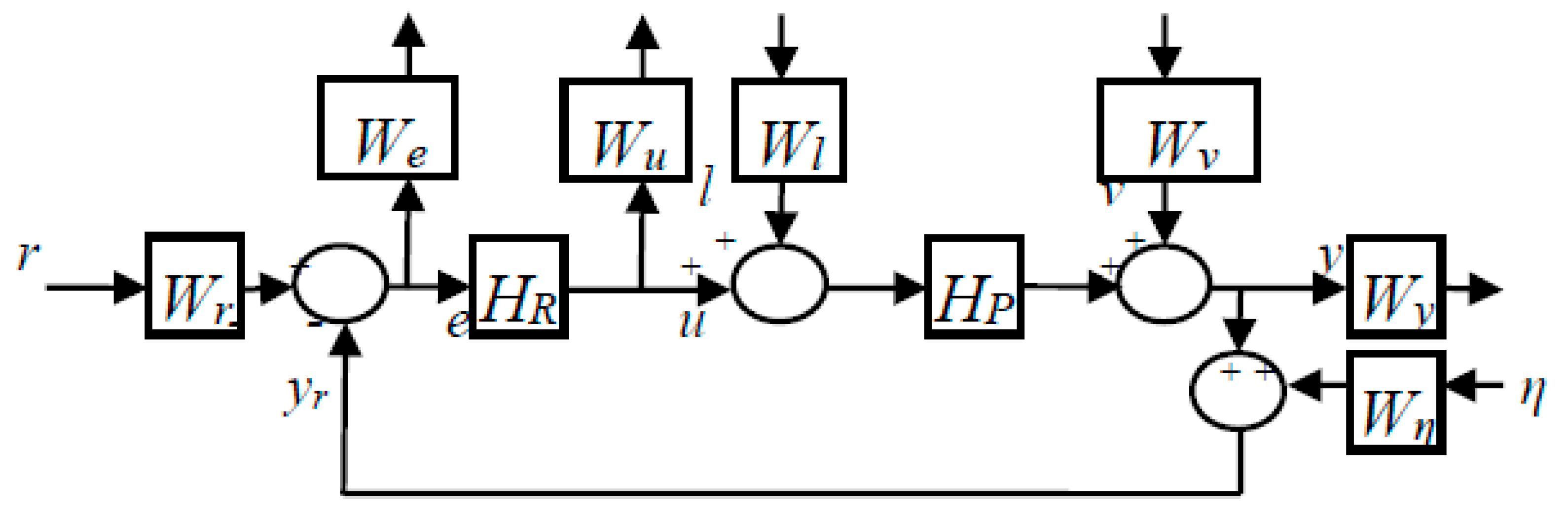
2. Recommendations for Choosing the Models for the Weighting Functions

The robustness performance requirements depend on the sensitivity functions, whose specifications are included in the frequency behavior models. If these sensitivity functions remain inside the imposed limits, the robustness objectives are met [2,3,4,5].

So, for a standard second order model, the sensitivity function depends on the damping ratio and natural frequency according to Figure 3a and relation:

$$S\left(s\right)=\frac{s^2+2\xi {\omega }_{n}s}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}.$$

(3)

On the other hand, the magnitude $M_S$ depends on the damping ratio, according to the relation:

$$M_S:={‖S‖}_{\infty }=\frac{x\sqrt{x^2+4{\xi }^2}}{\sqrt{4x^2{\xi }^2+{\left(1-x^2\right)}^2}},x=\sqrt{0.5+0.5\sqrt{1+8{\xi }^2}}.$$

(4)

As a result, the performance specifications can be given by:

$$\left|S\left(s\right)\right|\le \left|\frac{s}{s/M_S+{\omega }_{bs}}\right|,s=j\omega , \forall \omega ,{\omega }_{bs} \mathrm{is} \mathrm{the} \mathrm{bandwidth}.$$

(5)

In the ideal case, relation $\left|W_{e}S\right|\le 1$ provides the reference tracking to a step input signal (and a zero steady state control error), meaning:

$$W_e\le \frac{s/M_S+{\omega }_{bs}}{s}.$$

(6)

Important for the practical situations is to have a steady state error less than an imposed value ($\left|S\left(0\right)\right|\le {\epsilon }_S$). Thus, it is sufficient to choose $\left|W_e\left(0\right)\right|\ge 1/{\epsilon }_S$ (${\epsilon }_S$ is the tracking error), which can be achieved by correcting Function (6) with the modified form:

$$W_e\left(s\right)=\frac{\frac{s}{M_S}+{\omega }_{bs}}{s+{\omega }_{bs}{\epsilon }_S}$$

(7)

A proper design in terms of the sensitivity function is obtained if both conditions imposed to ${\omega }_{bs}$ and $M_S$ are satisfied according to the relations:

$${‖W_e\left(j\omega \right)S\left(j\omega \right)‖}_{\infty }\le 1,{‖S\left(j\omega \right)‖}_{\infty }\le \frac{1}{W_e\left(j\omega \right)},$$

(8)

where the upper limit (Figure 4a) is:

$$\frac{1}{W_e\left(s\right)}=\frac{s+{\omega }_{bs}{\epsilon }_S}{\frac{s}{M_S}+{\omega }_{bs}}.$$

(9)

For improved performances, Model (7) may have a higher order, as follows:

$$W_e\left(s\right)={\left(\frac{\frac{s}{M_S}+{\omega }_{bs}}{s+{\omega }_{bs}{\epsilon }_S}\right)}^k,k\ge 1.$$

(10)

For the noise sensitivity function, the weighting function $W_u\left(s\right)$ is chosen, which influences the control signal, u, according to the relations:

$$W_u\left(s\right)=\frac{s+\frac{{\omega }_{bu}}{M_u}}{{\epsilon }_{u}s+{\omega }_{bu}},{‖W_u\left(j\omega \right)R_S\left(j\omega \right)‖}_{\infty }\le 1,{‖R_S\left(j\omega \right)‖}_{\infty }\le \frac{1}{W_u\left(j\omega \right)}.$$

(11)

where $M_u$, ${\omega }_{bu}$, ${\epsilon }_u$ are the maximum gain, the bandwidth and the error. The upper limit is:

$$\frac{1}{W_u\left(s\right)}=\frac{{\epsilon }_{u}s+{\omega }_{bu}}{s+{\omega }_{bu}/M_u}.$$

(12)

The magnitude of $\left|R_S\right|$ on low frequency is essential to limit the control signal.

The procedure is similar for the complementary sensitivity function and the load sensitivity function.

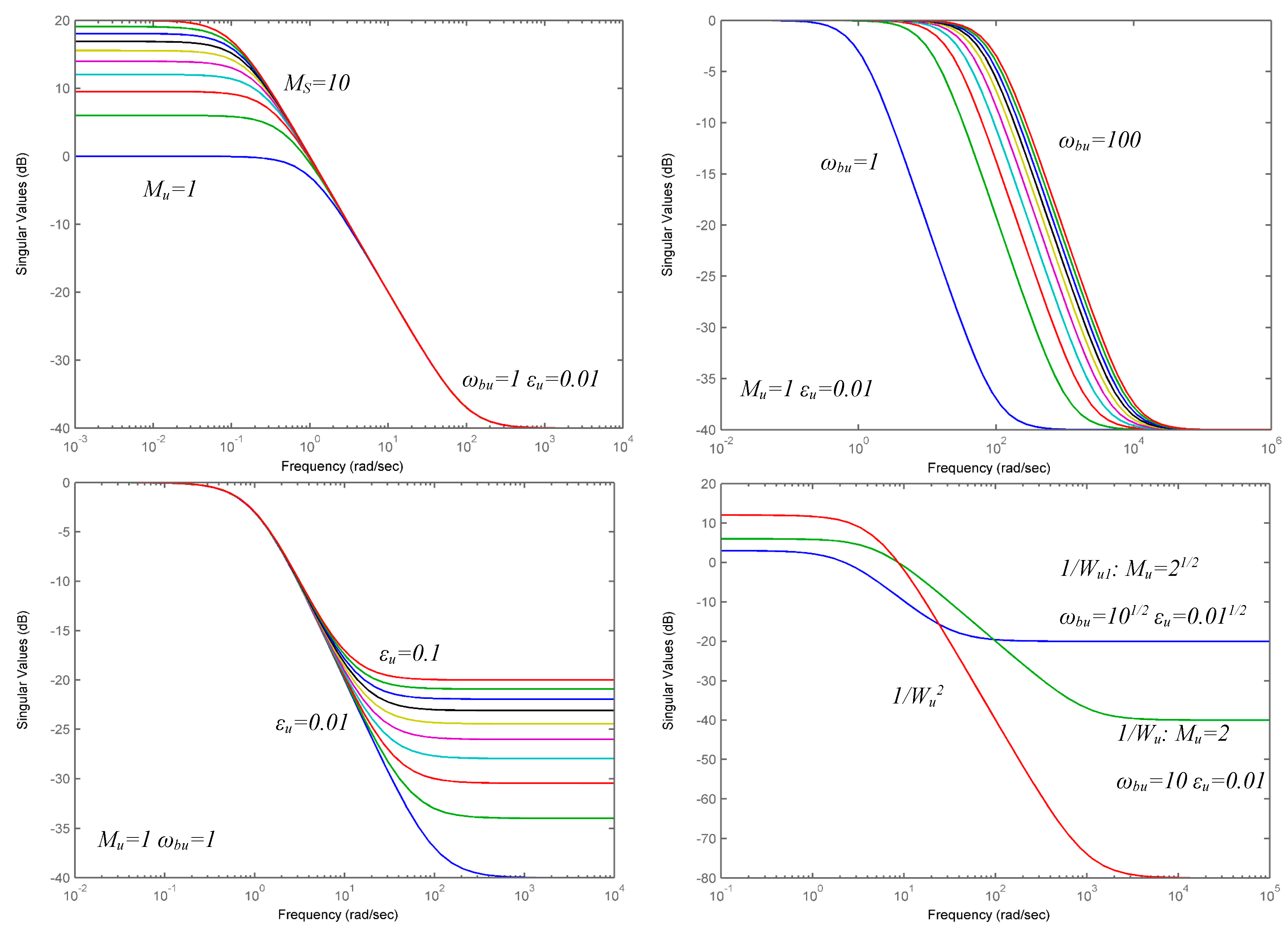
3. The Effect of the Parameters on the Weighting Functions

Several possibilities may be used in order to design the weighting functions. One possible choice is to consider a combination of cost functions providing the mixed-sensitivity formulation.

Figure 5 and Figure 6 show the behaviors imposed using the functions $1/W_e\left(s\right)$, Equation (9), and $1/W_u\left(s\right)$, Equation (12), considering different values of the parameters $M_S, {\omega }_{bs}, {\epsilon }_S,$ $M_u, {\omega }_{bu}, {\epsilon }_u$ [8,16].

The study of the dependencies on the shape of the weighting functions $W_e\left(s\right)$ and $W_u\left(s\right)$ highlights the importance of the following values for the magnitude $M_S, M_u=1, 2, 3,$ bandwidth ${\omega }_{bs}, {\omega }_{bu}=1, 2$ and errors ${\epsilon }_S, {\epsilon }_u>0.01$.

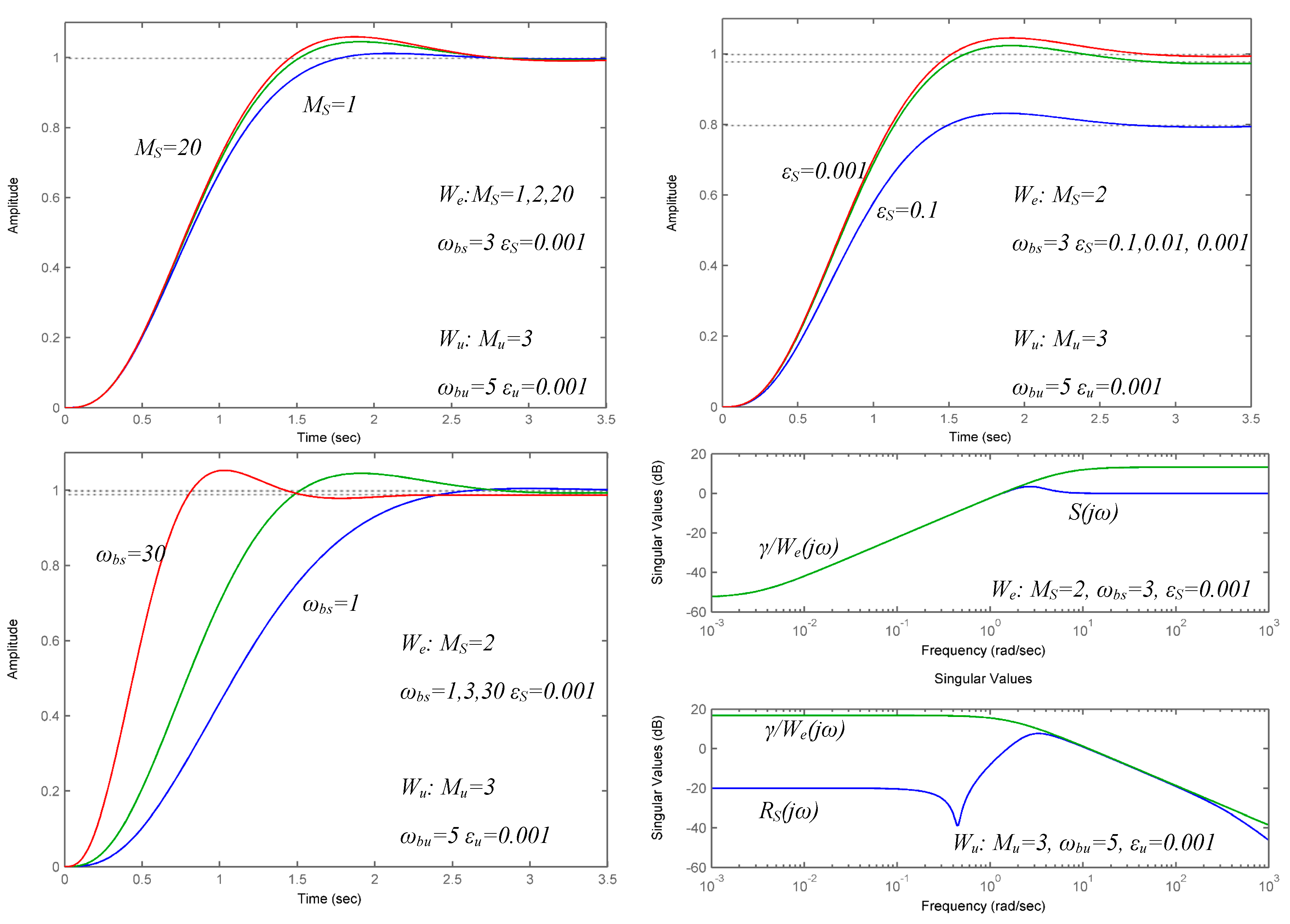
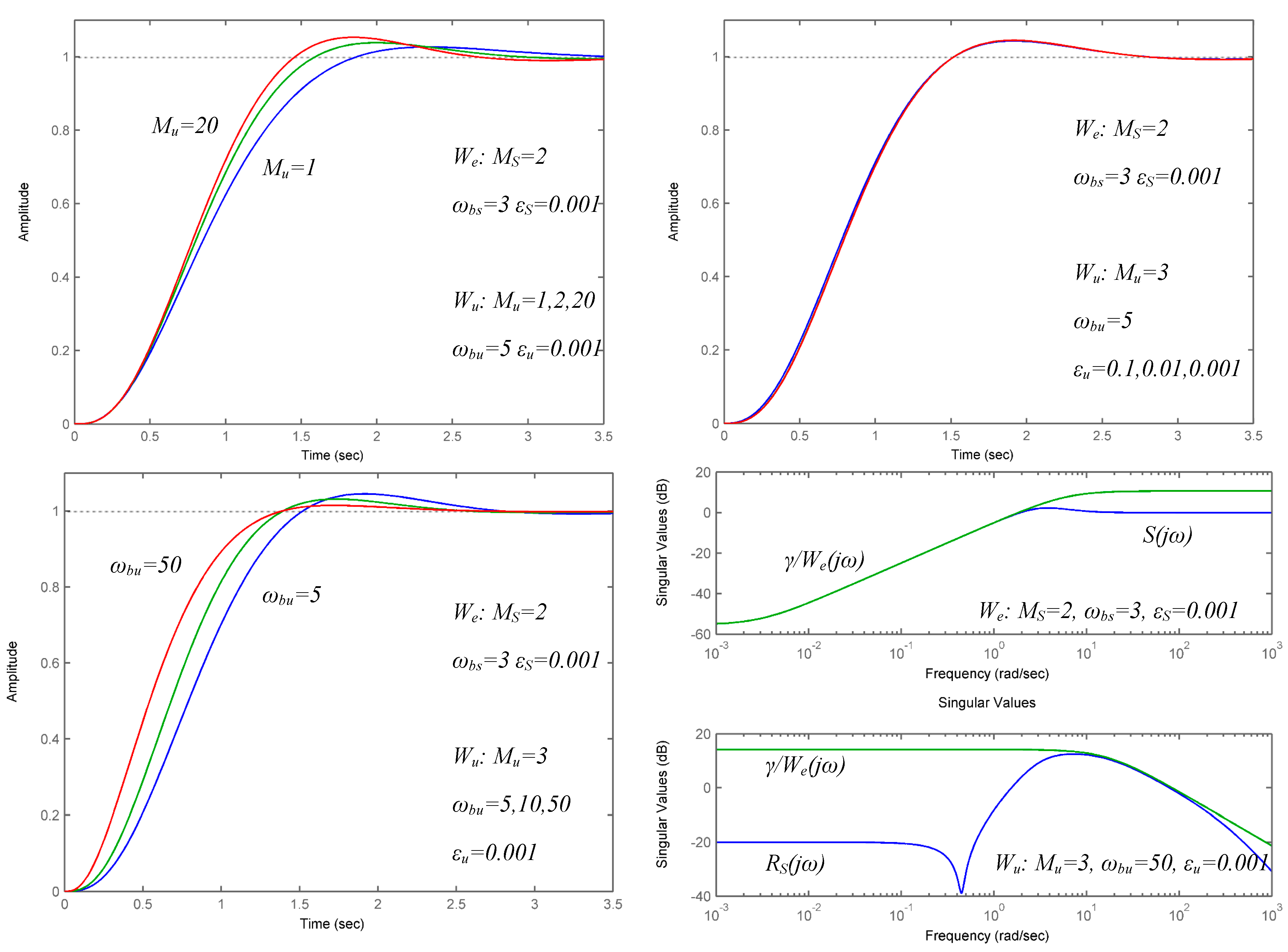
4. Results of the Analysis of the Closed-Loop Control System

The main objectives required in the control system (defined by the block diagram with the weighting functions from Figure 7) are: good reference tracking and a limited control signal [1,2,3,4,5].

The robust design consists in determining the controller H_R so that the H-infinity norm of the closed-loop transfer function is less than a positive number ($\gamma$):

$${‖\begin{array}{l}{W}_{e}S\\ W_u{H}_{R}S\end{array}‖}_{\infty }<\gamma$$

(13)

The plant model used for the case study of the closed-loop system from Figure 7 is described by the transfer function $H_p\left(s\right)=\frac{2}{s^2+0.05s+0.2}$.

The block diagram also includes the weighting functions and the controller designed using the H-infinity synthesis. The simulations from Figure 8 and Figure 9 show the behaviors of the system [13].

5. Conclusions

In this paper, a short study of the effects of the weighting functions on the performances of the robust control systems was presented.

In this context, the basic requirements imposed to the control system (from Figure 1) were:

• Reducing the control error, rejecting the disturbances and ensuring the desired performances;
• Reducing the effect of the variations of the parameters in the open-loop system on the transition to the closed-loop system, i.e., ensuring the robustness of the control system in case of uncertainties.

In the robust control diagram (Figure 2), the performances regarding the reference tracking, disturbances and measurement noise rejection and control signal effort should be achieved for each external input $r, v, \eta , l$, whose energy does not exceed a predetermined value. As a result, weighting functions must be properly designed and used.

So, for the weighting function $W_e\left(s\right)$:

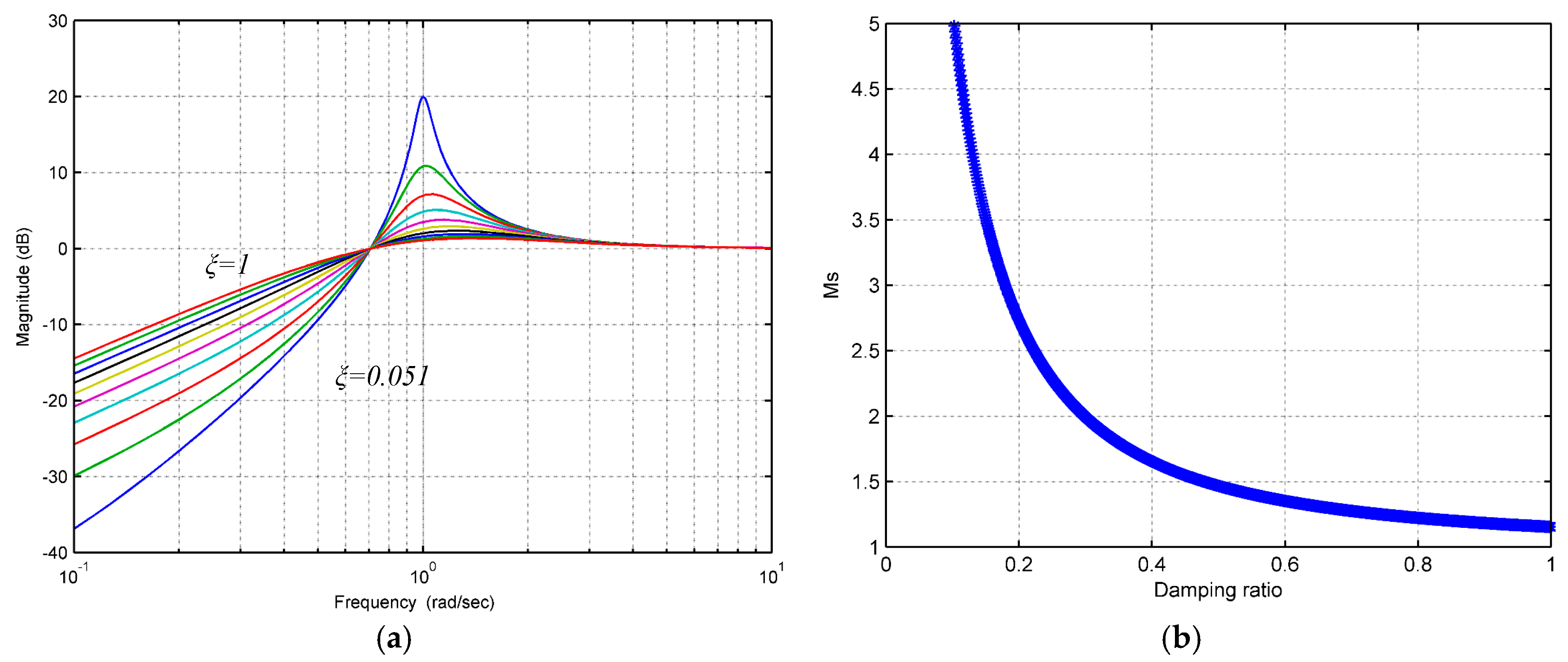
• Increasing the $M_S$ leads to a higher overshoot; reasonable values for the overshoot and for the gain (robustness) margin are obtained for $M_S\le 2$;
• Increasing the ${\omega }_{bs}$ leads to a lower transient time, meaning a faster response of the closed-loop system and a quick rejection of the disturbances; a higher value for ${\omega }_{bs}$ highlights a closed-loop system which is more sensitive to disturbances and parameter variations; a low value for ${\omega }_{bs}$ indicates a longer response time and a more robust system;
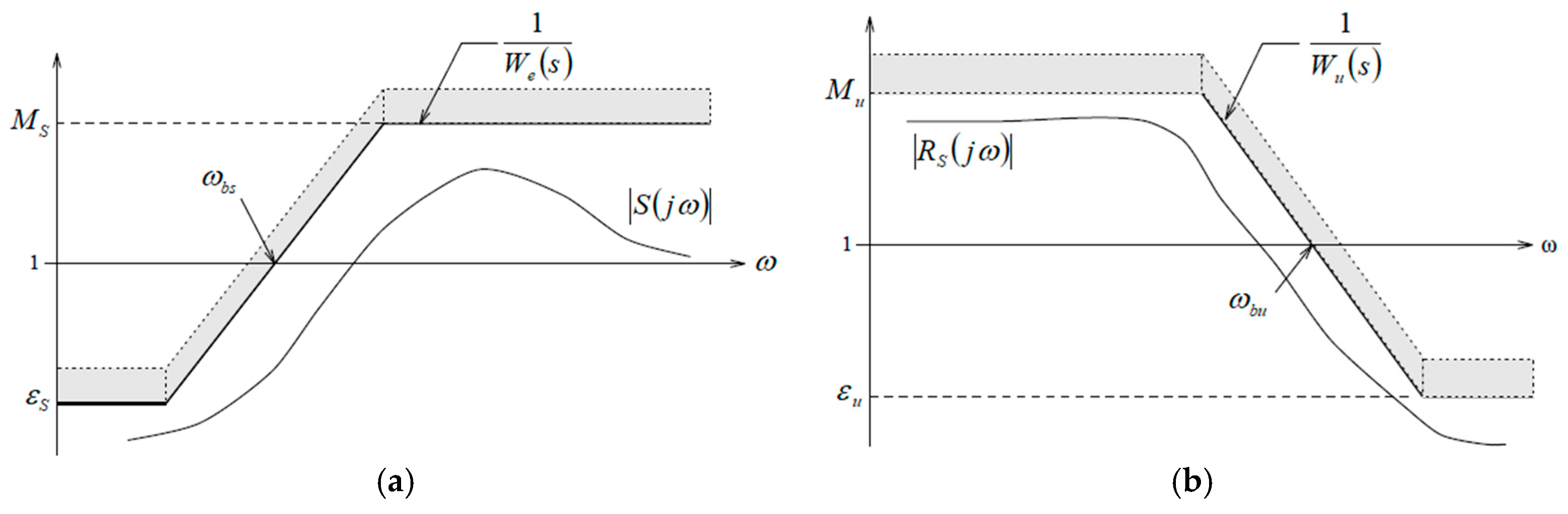
• A low value imposed to the ${\epsilon }_S$ (e.g., ${\epsilon }_S=0.1$) leads to a high steady state error; so, the recommended value is ${\epsilon }_S>0.01$ (e.g., ${\epsilon }_S=0.001, 0.0001$).
  At the same time, for the weighting function $W_u\left(s\right)$:
• $M_u$ it is chosen according to the restrictions imposed to the actuator; increasing the $M_u$ leads to a higher overshoot and a reasonable value is obtained for $M_u\le 2$;
• Increasing the ${\omega }_{bu}$ leads to a lower response time of the closed-loop system; a lower value of ${\omega }_{bu}$ assures a better limitation of the measurement noise;
• The value of ${\epsilon }_u$ does not significantly influence the performances of the closed-loop system.