Pseudo-Analysis as a Tool of Information Processing ^†

Abstract

The theory of the pseudo-analysis is based on a special real semiring (called also tropical semiring). This theory enables a unified approach to three important problems as nonlinearity, uncertainty and optimization, with many applications. There are presented applications in fuzzy logics and fuzzy sets, utility theory, Cumulative Prospect theory of partial differential equations.

1. Introduction

The first traces of the pseudo-analysis goes to Grossman and Katz [1] and Burgin [2] (what today is called g-calculus, see [3]), then Maslov [4] (what today is called idempotent analysis). These previous results were a starting point to develope a complete unified theory under the name pseudo-analysis [5,6,7,8,9,10,11], and as a special case the g-calculus [3]. This theory enables a unified approach to three important problems as nonlinearity, uncertainty and optimization, with many applications. Then corresponding pseudo additive measures and corresponding integrals were introduced. The usefulness of the pseudo-analysis is shown with some important applications in the theory of nonlinear equations, decision theory, fuzzy logics and fuzzy sets, information theory, option pricing, large deviation principle, cumulative prospect theory, physics of the universe, see [4,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21].

2. Pseudo-Analysis

The theory of the pseudo-analysis is based on the idea to introduce a special real semiring instead of the usual field of real numbers, with new operations so-called pseudo-addition and pseudo-multiplication, see [5,6,7,8,9]. These operations are related to aggregation functions (operators), see [17,18,19]. Aggregation of the information in an intelligent system is the basic problem, and its use is increasing in more complex systems, e.g., applied mathematics with probability, statistics, decision theory, computer sciences with artificial intelligence, operations research, as well as many applied fields as economy and finance, pattern recognition and image processing, data fusion, multi-criteria decision aid, automated reasoning, robotics, a fusion of images, integration of different kinds of knowledge, see [17,18,19].

It is considered an ordered semiring ([a, b], ⊕,⊗) on an interval [a, b] in [−∞,+∞], the operation ⊕ is called pseudo-addition and ⊗ is called pseudo-multiplication. Important special cases are: (i) ⊕ = max, ⊗ = +; (ii) ⊕ and ⊗ are generated with a monotone function g; (iii) ⊕ = max, ⊗ = min, see [7,8,9,11]. Special important pseudo-operations on the unit interval are triangular norms T, triangular conorms S, and uninorms, see [18]. Basic continuous t-norms are

TL(x, y) = max(0, x + y − 1),      TP(x, y) = xy,      TM(x, y) = min(x, y),

and corresponding dual t-conorms

SL(x, y) = min(1, x + y),      SP(x, y) = x + y − xy,      SM(x; y) = max(x, y).

3. Application: Fuzzy Logics and Fuzzy Sets

In the classical set theory, a subset A of the basic set X is completely given with its characteristic function ${\chi }_A:X\to \left\{0,1\right\}$, which is zero if the element does not belong to A, and has a value of one if the element belongs to the set A. In order to handle uncertain situations, when it is not quit clear whether an element belongs to the set, it is introduced the notion of fuzzy sets. Fuzzy subset A of X is given by membership function ${\mu }_A:X\to \left[0,1\right]$, where ${\mu }_A\left(x\right)$ has the meaning of a degree that the element $x\in X$ belongs to fuzzy set A, see [18]. For a t-norm T, the strong negation c given by c(x) = 1 − x, and with the t-conorm S dual to T given by

S(x, y) =c(T(c(x), c(y)),

We obtain the basic logic connectives in a [0, 1]-valued logic, see [8,18]:

conjunction: x ^T y = T(x, y);

disjunction: x vs. y = S(x, y).

The arithmetical operations with fuzzy numbers is based on Zadeh extension principle. Let T be an arbitrary but fixed t-norm and ■ a binary operation on R. An operation ■ is defined for fuzzy numbers A and B by the extension

A ■T B(z) = sup {T(A(x), B(y))| x■y = z} for z∈R.

Further, we have introduced in [20] a theory of linear fuzzy vector space, where the main point is the assumption that the distance between two imprecise points is a fuzzy set. We give only the basic definition. We call a fuzzy set fuzzy point $\tilde{P}$ at $P\in {\mathrm{R}}^n$, given by its membership function ${\mu }_{\tilde{P}}\in {ℱ}^n$, where ${ℱ}^n$ denotes all fuzzy points.

Definition 1.

A subset${\mathscr{H}}^n\subseteq {ℱ}^n$is called linear fuzzy space if its elements satisfies the following: Symmetric against the core$C\in {\mathrm{R}}^n$, i.e.,

$$(\mu \left(C\right)=1), \mu \left(U\right)=\mu \left(V\right)\wedge \mu \left(V\right)\ne 0 \Rightarrow d\left(C,U\right)=d\left(C, V\right),$$

where  $d\left(C, V\right)$ is the distance in${\mathrm{R}}^n$. Linearly decreasing with respect to the points’ distance from the core given by

For$r\ne 0$, we have

$$\mu \left(U\right)=\{\begin{array}{c}1-\frac{d\left(C,U\right)}{r} if d\left(C,U\right)<c\\ 0 if d\left(C,U\right)\ge c ,\end{array}$$

for$c=0$, we have

$$\mu \left(U\right)=\{\begin{array}{c} 1 if C=U \\ 0 if C\ne U , \end{array}$$

where$d\left(C,U\right)$is the distance between a point$U$and core$C$($U,C\in {\mathrm{R}}^n$) and$c\in {\mathrm{R}}^{+}$is a constant.

For many impotant applications see [20].

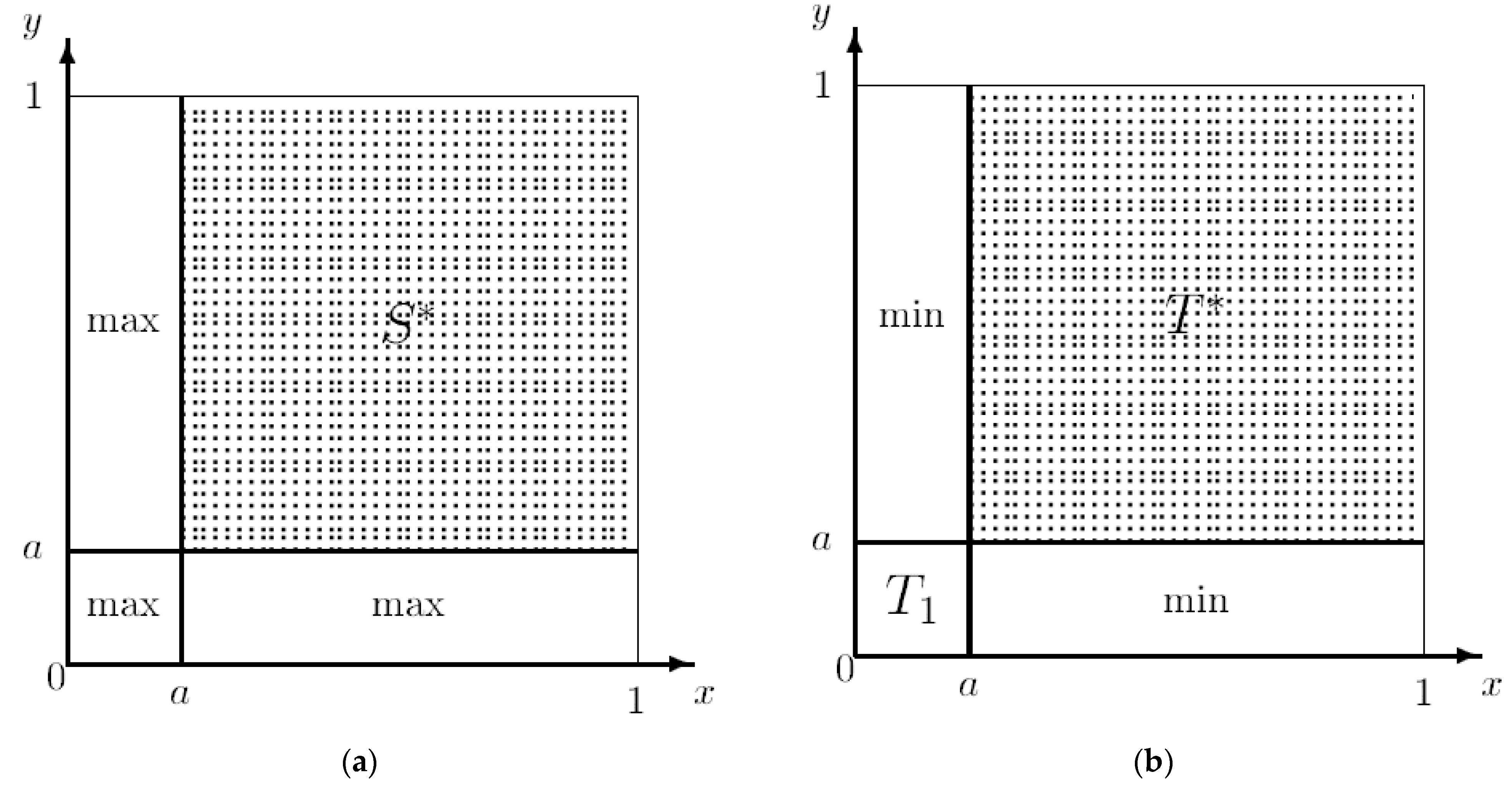
4. Application: Utility Theory

Another example of application is in the utility theory, which was earlier based on the notion of mathematical expectation in the axiomatic foundations by von Neumann and Morgenstern as probabilistic mixtures. The aim of the paper [12] was to extend maximally in a natural way the utility theory. The solution obtained in [12] is based on a result from [18] (Th. 5.21), on the restricted distributivity of a t-norm over a t-conorm:

Triangular normTis conditionally distributive over triangular normSif for every x,y,z$\in$[0, 1] holds

T(x,S(y, z)) =S(T(x, y),T(x, z)),

forS(y,z) < 1 (see Figure 1).

Theorem 1.

A continuous t-norm T is restricted distributive over a continuous t-conorm S if and only if there exists a ∈ [0, 1], a strict t-norm T* and a nilpotent t-conorm S* such that the additive generator s* of S* satisying s*(1) = 1 is also a multiplicative generator of T* such that T is represented by the ordinal sum T = (<0, a, T1>, <a, 1, T*>), where T1 is an arbitrary continuous t-norm and S = (<a, 1, S*>).

For a t-conorm S and a σ–algebra A of subsets of X a mapping m: A→[0, 1] is called a pseudo-additive measure, if m(∅) = 0, m(X) = 1 and if for all M,N∈A with M∩N = ∅, holds

m(M ∪ N) = S(m(M),m(N))

Using also some kind of necessary independence property the only possible pseudo-additive measures, requires conditionally distributive pairs (S, T) of conorms and t-norms. Therefore there are three possible cases:

• probality measures (and T = product);
• possibility measures (and T is any t-norm);
• normalized hybrid measure m such that there exists a∈[0, 1] such that for M and N disjoint

m(M∪N) = m(M) + m(N) − a for m(M) > a, m(N) > a and

m(M∪N) = max(m(M),m(N))      otherwise.

Therefore, there are only three reasonable mixtures: possibilistic, probabilistic, and a hybridization such that the mixture is possibilistic under a certain threshold, and probabilistic above (Figure), see [12].

We have developed an axiomatic system for hybrid probabilistic-possibilistic utility theory. Let X = {x₁, x₂, …, x_n} be the set of outcomes, and Δ(X) is the collection of S-measures given on X. The hybrid mixture combines two S-measures m and m′ in a new H(m,m′;c,d), where

(c,d)∈Φ_S,a = {(c,d)|c,d∈[0, 1], c + d = 1 + a or min(c,d) ≤ a, max(c,d) = 1}, for a∈[0, 1]

given by

H(m,m′;c,d) = S(T(c,m), T(d,m′))

for the pair (S, T) which satisfies restricted distributivity equation. The behavior of the decision maker can be easily interpreted using Figure. Now we give axioms for the preference relation ≤ _h given on Δ(X) which gives the optimistic utility function:

H1. 

Δ(X) is with complete pre-ordering ≤ _h, i.e., ≤ _h is reflexive, transitive and complete.

H2 (Continuity).

If m < _h m′ < _h m″, then∃c∈[a,1]: m′ ~ _h H(m,m″;1 + a − c,c), for m,m′,m″ > a; otherwise∃c∈[0,a]: m′ ~ _h H(m,m″;1,c).

H3 (Independency).

For ∀m,m′,m″∈Δ(X) and all c,d∈Φ_S,a it holds m′ ≤ _h m″⇔ H(m′,m;c,d) ≤ _h H(m″,m;c,d).

H4 (Uncertainty).

m ≤ _h m′ ⇒ m ≤ _h H (m,m′;α,1 + a − c) ≤ _h m′, c∈[a,1], for m,m′ > a; m < m′ ⇒ m < _h m′, otherwise.

We introduce the so-called optimistic utility function for m∈Δ(X) in the following way

$$U^{+}(m)=S_{x_i\in X}\left(T\left(m(x_i),u(x_i)\right)\right),$$

for a preference function u:X→U which corresponds to each consequence of X a preference level of U, with u⁻¹(1) ≠ ∅ ≠ u⁻¹(0). We remark that U⁺ preserves hybrid mixture. The following theorem gives complete characterization of the optimistic hybrid utility.

Theorem 1 (on representation).

Let≤ _h be a binary preference relation on Δ(X). Then the relation ≤ _h satisfies axioms {H1,H2,H3,H4} if and only if there exists linearly ordered scale of utility U, with inf(U) = 0 and sup(U) = 1, and a preference function u:X→[0, 1], such that m ≤ _hm′ if and only m□_um′, where □_u is an ordering in Δ(X) induced by optimistic utility function given by U⁺(m) = S_xi∈X(T(m(x_i), u(x_i)), for (S,T) a conditionaly distributive pair of continuous t-conorm and t-norm.

5. Application: Cumulative Prospecct Theory

Modeling decision procedures with aggregation functions special place deserve non-additive integrals based on fuzzy measures, since they take in the account the interaction between entrances. Therefore, they have many important applications in mathematics, engineering and economics, optimization. Among them are the Choquet integral and Sugeno integral, see [7]. We highlight these two types of integrals for finite set. Let $\mu$ be a monotone measure on Ὠ and $f$ a function defined on Ὠ and with values in the set of nonegative real numbers and with finite set of values $\left\{a_1,a_2,\dots ,a_n\right\}$, whit $a_1$< $a_2$<…< $a_n$. Choquet integral ($C$) ${\displaystyle \int f\left(x\right)d\mu \left(x\right)}$ is given by.

$$(C){\displaystyle \int fd\mu }={\displaystyle \sum _{i=1}^n\left(a_i-a_{i-1}\right)\cdot \mu \left(\left\{x|f\left(x\right)\ge a_i\right\}\right)}.$$

For $\mu$ a normalized monotone measure on Ὠ and $f$ is a function on Ὠ with values $\left\{a_1,\dots ,a_n\right\}$, where $0\le a_1\le \dots \le a_n\le 1$, Sugeno integral ${\displaystyle \int f\left(x\right)\circ \mu \left(x\right)}$ is given by (finite case) ${\displaystyle \int f\circ \mu }=\underset{i=1}{\overset{n}{\vee }}\left[a_i\wedge \mu \left(\left\{x|f\left(x\right)\ge a_i\right\}\right)\right]$.

For the purpose for comparing two decisions amounts regarding two pairs of sets, the positive and negative features of the alternatives it was introduced a generalization of Expected Utility and Choquet Expected Utility, under the bipolar perspective, Cumulative Prospect Theory (CPT) was introduced. We have introduced CPT-like integral-based premium principle related to the concept of symmetric operations is introduced in [21], and we have shown by an example that in some decision problems the previous monotone integral-based functionals are not appropriate decision-making tools, but our CPT-like integral works. Let ${\mathcal{M}}_b$ be the class of all monotone measures m such that $m(\Omega )=b$. Let ${ℱ}_a$ be the class of all insurance risks $f:\mathrm{\Omega }\to \left[-a,a\right]$. The integral-based premium principle is some rule $\mathrm{\Pi }:ℱ\times \mathcal{M}\times \mathcal{M}\to R$ which corresponds premium $\mathrm{\Pi }(f,m_1,m_2)$ to the insurance risks $f:\mathrm{\Omega }\to R$. Some well-known examples are: The net premium principle, is defined for $f\in ℱ$ and probability $m=p\in M_1$ as

$$E(f)={\displaystyle {\prod }_N(f,p,p)}=I(f^{+},p)-I(f^{-},p).$$

The distortion premium principle, is defined for $f\in ℱ$ and $p\in {\mathcal{M}}_1$ as

$${\displaystyle {\prod }_{DPP}(f,m,m)}=I(f^{+},m)-I(f^{-},\overline{m}),$$

for $m=g\circ p$ and nondecreasing distorsion function $g:\left[0,1\right]\to \left[0,1\right]$, $g\left(0\right)=0$,$g(1)=1$.

The mean premium principle, for $f\in ℱ$, probability $p\in {\mathcal{M}}_1$ and increasing function $\varphi$, $\varphi (0)=0$, is given by

$${\displaystyle {\prod }_M(f)={\varphi }^{-1}}(I(\varphi (f),p))$$

The exponential premium principle for$f\in ℱ$, probability $p\in {\mathcal{M}}_1$ and $\alpha >0$ is given by

$${\displaystyle {\prod }_{\exp }(f)}=\frac{1}{\alpha }\ln (I(e^{\alpha f},p))$$

Now we give the general definition from [21].

Definition 2.

The generalized CPT-like integral-based premium principle

$${\mathrm{\Pi }}_{CP{T}_{\varphi }}:{ℱ}_a\times {\mathcal{M}}_b\times {\mathcal{M}}_b\to R$$

for an insurance risk$f\in {ℱ}_a$and$m_1,m_2\in {\mathcal{M}}_b$is defined by

$${\mathrm{\Pi }}_{CP{T}_{\varphi }}(f,m_1,m_2)={\varphi }^{-1}(I(\varphi (f^{+}),m_1)-I(\varphi (f^{-}),\overline{m_2})),$$

for odd, increasing, continuous function$\varphi :[-a,a]\to \left[-\infty ,\infty \right]$, $\varphi (0)=0$, $\varphi (a)=\infty$

Specialy, for $\varphi (x)=x$, and $m_1=m_2=P$ probability we obtain ${\mathrm{\Pi }}_{CP{T}_{\varphi }}={\mathrm{\Pi }}_N$. If $\varphi$ is an odd function and $m_1=m_2=P$ probability we obtain ${\mathrm{\Pi }}_{CP{T}_{\varphi }}={\mathrm{\Pi }}_M$. We have given in [21] a complete characterization for the CPT-like integral-based premium principle and we have investigated its main properties. Further development of integrals based on pseudo-analysis is obtained in [22,23].

Recent approach [24] is based on important operation copula, see [25].

6. Application: Partial Differential Equations

Pseudo-analysis is very useful in the theory of nonlinear equations (ODE, PDE, difference equations, etc.). The basic tool is the pseudo-superposition principle [8,12,14], i.e., for solutions of a nonlinear equation u1 and u2, then also a1 ⊗ u1 ⊕ a2 ⊗ u2 is a solution of the considered equation for any constants a1 and a2 from [a, b].

Important contribution of the pseudo-analysis is the fact that it enables an exact solution of the Burgers equation. It is very important in treating the general Hamilton–Jacobi equation. We remark that the nonlinear Hamiltonian was non-smooth, what is important in control theory. For Hamilton-Jacobi equation, where H is a convex function, then pseudo linear combination a1 ⊗ u1 ⊕ a2 ⊗ u2 is also a solution of the preceding Hamilton-Jacobi equation, with respect to pseudo-operations ⊕ = min and ⊗ = +.