Informational Approaches Lead to Formulations of Quantum Mechanics on Poincaré Disks †
Abstract
:1. Introduction
2. Pars construens: Hyperbolic Dynamics and Quantum Mechanics
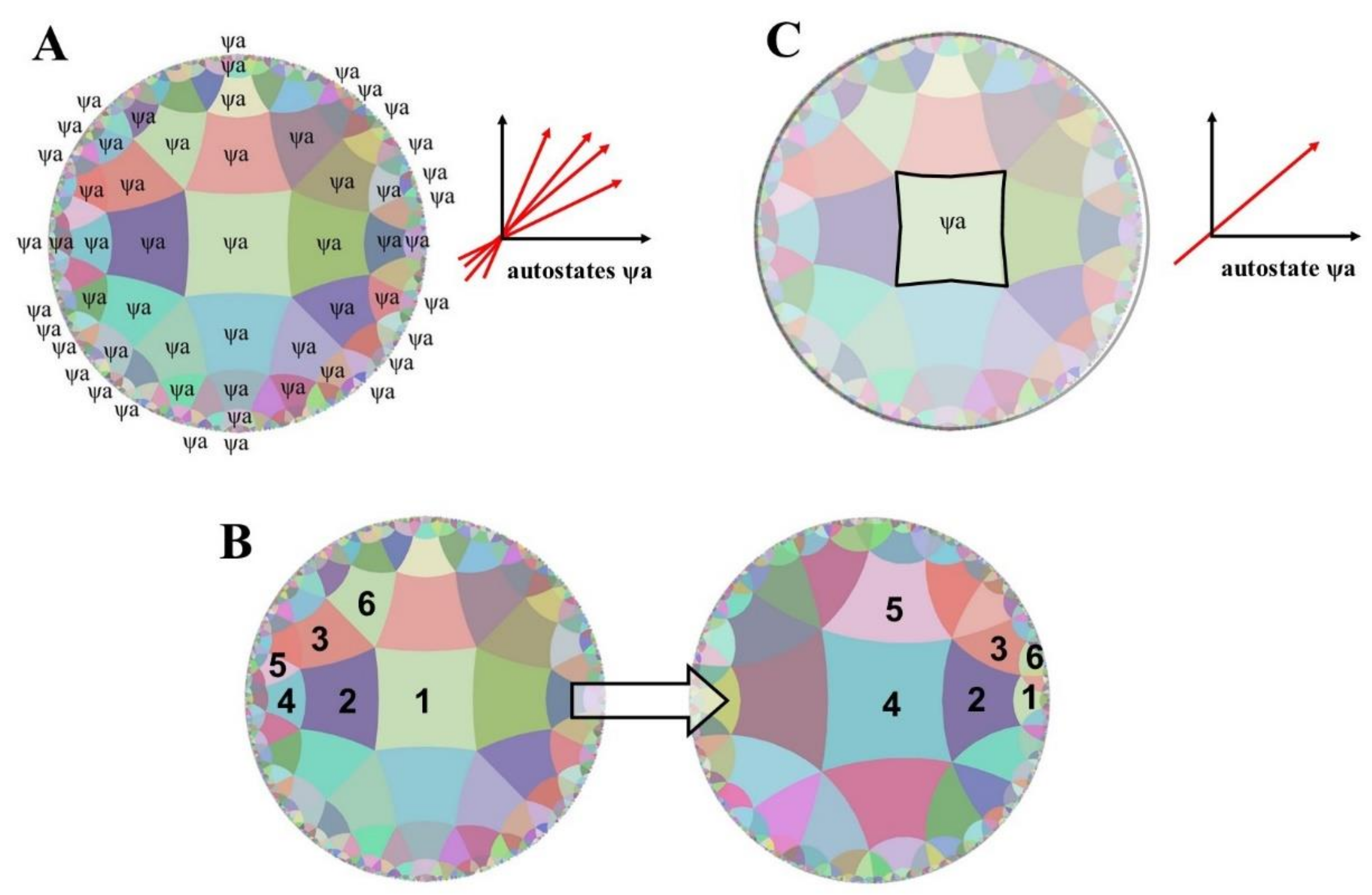
2.1. Before Measuring
2.2. After Measuring
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dales, R.C. The Problem of the Rational Soul in the Thirteenth Century; Brill: Leiden, The Netherlands; New York, NY, USA; Köln, Germany, 1995. [Google Scholar]
- The BIG Bell Test Collaboration. Challenging local realism with human choices. Nature 2018, 557, 212–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tozzi, A.; Peters, J.F. Information-devoid routes for scale-free neurodynamics. Synthese 2021, 199, 2491–2504. [Google Scholar] [CrossRef]
- Curtright, T.L.; Fairlie, D.B.; Zachos, C.K. A Concise Treatise on Quantum Mechanics in Phase Space; World Scientific: Singapore, 2014; ISBN 9789814520430. [Google Scholar]
- Piazza, L.; Lummen, T.T.; Quiñonez, E.; Murooka, Y.; Reed, B.W.; Barwickm, B.; Carbonem, F. Simultaneous observation of the quantization and the interference pattern of a plasmonic near-field. Nat. Commun. 2015, 6, 6407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tegmark, M. The Mathematical Universe. Found. Phys. 2008, 38, 101–150. [Google Scholar] [CrossRef] [Green Version]
- Cassinelli, G.; Lahti, P. Quantum mechanics: Why complex Hilbert space? Philos. Trans. A Math. Phys. Eng. Sci. 2016, 375, 20160393. [Google Scholar] [CrossRef] [PubMed]
- Dirac, P.A.M. The Fundamental Equations of Quantum Mechanics. Proc. R. Soc. A Math. Phys. Eng. Sci. 1925, 109, 642–653. [Google Scholar] [CrossRef] [Green Version]
- Gisin, N.; Fröwis, F. From quantum foundations to applications and back. Philos. Trans. A Math Phys. Eng. Sci. 2018, 376, 20170326. [Google Scholar] [CrossRef] [Green Version]
- Batygin, K. Schrödinger evolution of self-gravitating discs. Mon. Not. R. Astron. Soc. 2018, 475, 5070–5084. [Google Scholar] [CrossRef] [Green Version]
- Cartas-Fuentevilla, R.; Berra-Montiel, J.; Meza-Aldama, O. Hyperbolic ring-based formulation for thermo field dynamics, quantum dissipation, entanglement, and holography. Eur. Phys. J. C 2020, 80, 603. [Google Scholar] [CrossRef]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605. [Google Scholar] [CrossRef]
- Khrennikov, A. Hyperbolic quantum mechanics. Adv. Appl. Clifford Algebras 2003, 13, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Cariñena, J.F.; Rañada, M.F.; Santander, M. The quantum free particle on spherical and hyperbolic spaces: A curvature dependent approach. J. Math. Phys. 2011, 52, 072104. [Google Scholar] [CrossRef] [Green Version]
- Iomin, A. Exponential spreading and singular behavior of quantum dynamics near hyperbolic points. Phys. Rev. E 2013, 87, 054901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kollár, A.J.; Fitzpatrick, M.; Houck, A.A. Hyperbolic lattices in circuit quantum electrodynamics. Nature 2019, 571, 45–50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, A. Informational Approaches Lead to Formulations of Quantum Mechanics on Poincaré Disks. Proceedings 2022, 81, 20. https://doi.org/10.3390/proceedings2022081020
Tozzi A. Informational Approaches Lead to Formulations of Quantum Mechanics on Poincaré Disks. Proceedings. 2022; 81(1):20. https://doi.org/10.3390/proceedings2022081020
Chicago/Turabian StyleTozzi, Arturo. 2022. "Informational Approaches Lead to Formulations of Quantum Mechanics on Poincaré Disks" Proceedings 81, no. 1: 20. https://doi.org/10.3390/proceedings2022081020
APA StyleTozzi, A. (2022). Informational Approaches Lead to Formulations of Quantum Mechanics on Poincaré Disks. Proceedings, 81(1), 20. https://doi.org/10.3390/proceedings2022081020





