Learning Computing from Nature: Reflection on the Klein Four-Group ^†

Abstract

Information integration has been considered the key characteristic of the mechanism of consciousness. However, the mechanism of integration remains unknown. Integration can be considered in terms of the factorization of mathematical structures. This paper presented information integration as a mode of encoding information. The level of integration is reflected in the logic of encoding. The frequent occurrence of Klein’s Four-Group in relevant contexts provides some clues about the integrating logic of encoding information.

1. Introduction

Qualification of computing as natural can be interpreted in many essentially different ways. It is understood here as the functioning of models of the information transformation acquired through abstraction from similar processes in natural phenomena occurring without any engagement of human purpose-oriented action. In a slightly oversimplified distinction, natural computing is discovered while artificial is invented. A Turing Machine could qualify as a natural computing device (human computers described by Turing in his revolutionary 1936 paper did not have any idea about the purpose of their work being different from earning money for a living), but its special version of the Universal Turing Machine as artificial (it was not derived from an observation of a natural process and it was designed with the specific purpose of the simulation of all other Turing Machines). Another example of natural computing, probably less problematic in the qualification as natural, can be identified in the Artificial Neural Networks derived from the observation of natural neural systems. Certainly, a better name would have been Abstract Neural Networks, but this is not our concern.

The subject of this study was the continued exploration of a new and essentially different form of natural computing associated with consciousness and conceptualized as information integration [1,2]. The main difference between modeling natural phenomena occurring in neural networks and modeling information integration interpreted as consciousness is in the process of their observation. Natural neural networks can be investigated using traditional neuro-physiological methods of empirical inquiry that entirely eliminate the involvement of subjective experience. The study of consciousness not only necessarily involves subjective experience, but also makes it the central object of the inquiry. This does not mean that consciousness cannot be considered a natural phenomenon, at least in our understanding of the natural. It is important to make a clear distinction between the study of the traditional oppositions of mind-body or mental-physical qualifying phenomena according to the way we experience them or access them for our inquiry and the study of the structural characteristics of consciousness.

Many components of our mental experience are not conscious, for instance, retrieval of information. Moreover, the content of our phenomenal consciousness is obviously accessible to introspection and we have some level of control of this content, for instance, intentional initiation of the search of memory. However, the process of retrieval from memory can be, and usually is, beyond the access of consciousness. Additionally, we can perform quite complex actions (e.g., driving a car) without being in conscious control of it and without being able to retrieve it from memory. Even within conscious experience, we can distinguish different levels of awareness associated with focusing or shifting attention. However, consciousness, otherwise devoid of characteristics attributed to elements of its content, has only one striking feature of being a whole, in the philosophical tradition expressed as being one.

The presence of non-conscious mental phenomena and our ability to perform complex actions without any engagement of consciousness are sufficient arguments against the a priori assumption that consciousness is produced by the human neural system or any other already known physiological mechanism of the human organism. There are only two alternative assumptions that can be reasonably made. Consciousness is integrated information or its content is a product of an information integrating mechanism. The delicate issue of the difference between these two is outside of the scope of this paper and in this paper, the latter was assumed. The subject of this paper was the search for a mathematical model of such a mechanism considered as a natural computing device. Surprisingly, Klein’s Four-Group gives us a hint for the direction of this search.

2. Information Encoding

In my earlier work on modeling consciousness and the attempts to create conscious artifacts, I provided arguments for the claim that the missing component of computing AI devices is in encoding information [2]. In virtually the entire literature of the subject, encoding is considered arbitrary and irrelevant. Indeed, the number of characters or their choice does not make any difference for a Turing Machine as long as their set is finite. However, it does not mean that the way of encoding is trivial or irrelevant for the processing of information. Encoding and decoding of information are the missing links engaging the human intelligence of a programmer. This is the point where the meaning is lost as “irrelevant to the engineering problem” [3]. Can a Turing Machine tell you the meaning of the sequence 1,0,0 on its tape? Only a human programmer/engineer can tell you whether it is decimal 4 or 100 based on the way the information was encoded.

Encoding of information can be associated with the “logarithmic” set operation opposite to the creation of a power set. When we have a set S of n elements, T, a set of k elements, and k is the lowest natural number such that k ≥ log₂(n), then every element of S can be encoded as a subset of T. Of course, T can be much smaller than S. The set S can be infinite, but then the set T has to be infinite, or encoding has to be not by subsets of T, but by functions from a set U of lower cardinality than S, but still infinite, to the set T (positional digital systems).

In this brief exposition of the idea of encoding, we consider the finite case here where both S and T are finite. We can see that the encoding of S is an injective function from S to the power set 2^T of T, which has the natural structure of a Boolean algebra with respect to the partial order of set inclusion. This Boolean algebra (understood as a distributive ortholattice) will be called the logic $\mathcal{L}$ of the encoding [4]. A simple example of an information processing system of this type can be given by the Young-Helmholtz model of human color vision. The eye has three types of color receptors with two states that can be simply on or off, i.e., T = {R,G,B} and encoding is by the selection of subsets of T. The variety of eight colors from the set S with eight elements can be detected as it can be illustrated by the Venn diagram for three sets. The subsets of T can be associated with the sensations of colors (qualia) as encoded information. The set S can have more than eight colors (qualities or properties), but in this model, only eight can be perceived. Of course, in human vision, the receptors have some distributions of sensitivity and the incoming light can have different intensities of colors, so the Young-Helmholtz model is a gross oversimplification, but this is not important here. The crucial point is that our familiar Boolean logic is a consequence of the way information is encoded and, once it is encoded, how it is processed.

Boolean logic is not the only type possible, as the logic depends on the way encoding is performed or on how the artificial systems are designed. The idea of a circuit performing a function of ordering multiple inputs into an ordered output of smaller size can be found in the digital logical design of standard computer science in the form of a priority encoder [5]. In this case, the logic $\mathcal{L}$ is simply a linear order (every two elements are comparable). Moreover, the circuit works on already encoded information (typically in the binary form) and its function is just to order incoming encoded information. However, the two different logics open the way for the study of further alternatives.

3. Information Integration

Information integration requires a prior idea of the meaning of being integrated, being an indivisible whole. Here comes mathematics, where this concept is omnipresent. At the lowest level, we have this irreducibility into components in the distinction of prime numbers, numbers which cannot be products of other numbers. This ancient concept of irreducibility into products re-appeared in the study of a large variety of structures together with the idea that we can combine structures by generating analog structures on the direct products of components. It turns out that Boolean algebras (considered as lattices with orthocomplementation) are completely reducible into the simplest possible two-element Boolean algebras. This applies to the much wider class of distributive lattices. The complete reducibility of a lattice can be used as a test for distributivity [4].

This brings us to the main point of the idea of information integration as an encoding that has its logic $\mathcal{L}$ irreducible. Certainly, both examples considered above have distributive, i.e., completely reducible logics (linear orders are distributive). However, we have examples of quantum logic that are irreducible into products. Additionally, there is a large variety of lattices (potential logics of encoding) that are partially reducible to not necessarily small irreducible components. In such cases, we can have partial integration. In a general case, we can consider a gate (in my earlier papers on the subject called a General Venn Gate, which has as its mathematical model an injective function from a set S to the logic of encoding $\mathcal{L}$, where this logic is realized as a lattice of (not necessarily all) subsets of some set T). The level of integration corresponds to the level of the irreducibility of the logic.

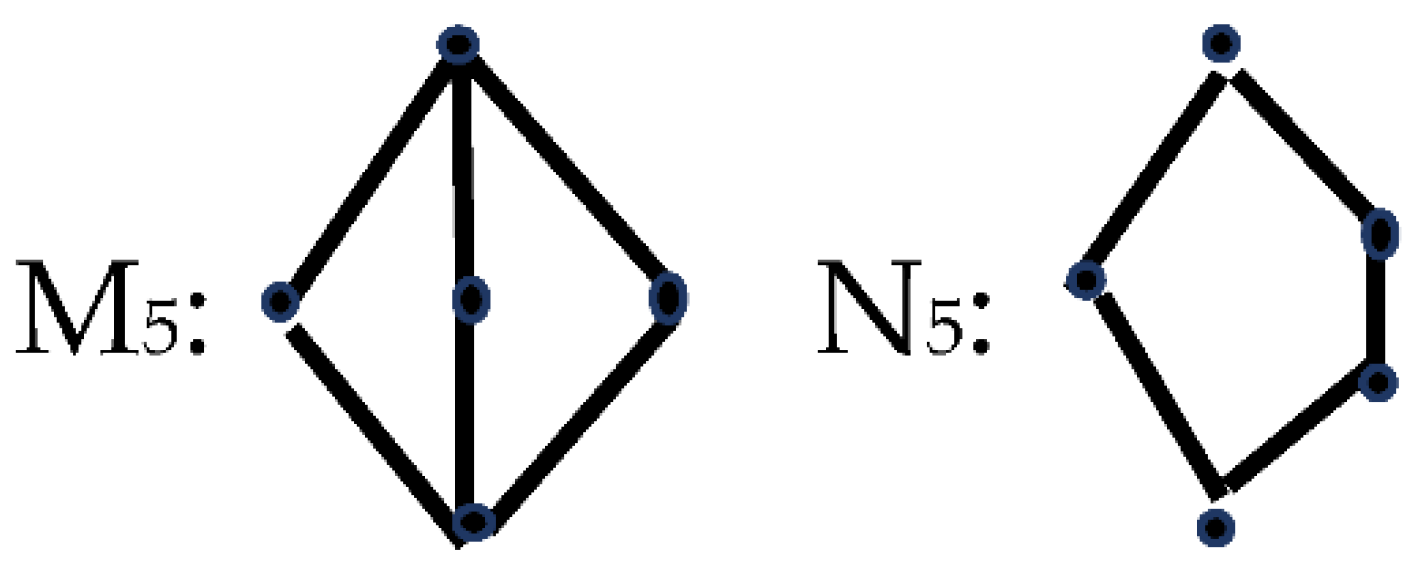
When we want to test a lattice for being distributive (completely reducible), we can use as a criterion the presence of two sublattices called M₅ and N₅ (Figure 1).

Lattices that have either M₅ or N₅ as sublattices are not distributive (i.e., they are reducible to products of component lattices. Lattices which have N₅ as sublattice are not modular (a weaker than distributivity but fundamental property of lattices) [5] (p. 11).

Since we are interested in the logic of integration, the natural question is whether there is a criterion for the level of integration. The criterion is in the structure of the so-called center of the lattice which consists of the elements which correspond to the pair on the top and the bottom elements of the component lattices in the decomposition of the lattice into a product [4] (p. 67). The center of the lattice (actually every bound poset) is always a Boolean lattice. If this Boolean lattice is trivial (with only two elements), the lattice is completely irreducible. Thus, the size of the center is a measure of reducibility. The center of a Boolean lattice is the entire lattice.

We have to add that Boolean algebra has in addition to the structure of a distributive lattice additional operation of othocomplementation corresponding in logic (understood as a discipline) to the negation. Orthocomplentation does not have any direct relationship to the property of irreducibility. It may be present in the completely irreducible quantum logic, but there is no compelling reason to include orthocomplementation as a necessary component of the logic of encoding.

4. Quantum Brain?

The natural candidate for the logic of information integration is quantum logic that is (almost) completely irreducible. The qualification “almost” prevents confusion. While the pure quantum logic is completely irreducible, the presence of the so-called superselection rules separating states which cannot enter superposition may require that quantum logic can have a nontrivial center. However, we can ignore this special case.

This choice of quantum logic seemed quite reasonable when we consider the long history of the attempts to explain consciousness as a quantum phenomenon. The most mysterious features of this description of reality at the microscale are the superposition of the states of the system and the entanglement of quantum objects. Both involve unknown in classical mechanics integration into an irreducible whole. However, all attempts to explain the unity of consciousness in terms of quantum-mechanical phenomena, from the holographic consciousness to microtubule models of Hameroff and Penrose, failed to provide a convincing description of the quantum mechanism in the brain, which could maintain necessary quantum coherence for more than a small fraction of a second.

I proposed to avoid using quantum-mechanical phenomena for the explanation, but rather to use mathematical formalism to create models for searching possible mechanisms not involving actual known quantum mechanical objects [1,2]. This view could raise the objection of how to explain that consciousness would have quantum features, but without being a quantum phenomenon. How do we explain the common theoretical features of consciousness and quantum systems? My response was that these commonalities are the result of the way we conceptualize physical reality in which, of course, human consciousness is involved. So, the short answer is that it is not consciousness that reflects quantum mechanical characteristics, but the other way around: quantum mechanical description of reality reflects the way of how our view of the world is influenced by the information integration in the mechanisms of consciousness [2,6,7].

We do not need quantum mechanical formalism to look for the structures in which irreducible lattices are involved. For instance, the lattice of subspaces of any vector space is completely irreducible. The role of the concept of a vector space in the formalization of the concept of geometric space is so important that this can explain our perception of space as an irreducible whole. The problem is not in the scarcity of irreducible lattices serving as candidates for the logic of encoding information into consciousness, but too big a choice of them. This is why Klein Four-Group is so interesting instead of being the smallest nontrivial (i.e., non-cyclic) group.

5. Klein Four-Group

Finally, we can consider the curious role of the Klein group. Why should we be interested in it in the search for an appropriate logic of information integration that can be considered a model for consciousness? The group has only four elements and can be defined by group presentation V = <a,b|a² = b² = (ab)² = e>. It is present in logic and computer logic design as it can be identified with one of the 16 logical operations XOR. However, in logic, it does not have a prominent role such as NAND (one of the two logical operations which can be used to generate all other logical operations). XOR is distinguished only by the fact that it is an invertible operation, i.e., it defines a group. This does not explain much.

This brings us to the next natural question of why we should be interested in any group, this particular one or any other. Here the answer is much simpler. Every group can be identified as a subgroup of the group of transformations of some set. Cayley initiated the general group theory by this statement in the 19th century. The triumphal march of the concept of a group to the central position in the entire mathematics and later all physical sciences was accelerated by its use in Klein’s 1872 Erlangen Program of the unification of geometry as a theory of symmetry, i.e., invariants of the groups of geometric transformations.

The main tool of the study of symmetries and their breaking (transition to the lower level of symmetry) in mathematics and physics is the structure of subgroups of a group of transformations. The most important developments in modern physics were transitions between different symmetries in the description of reality. For instance, the transition from classical mechanics to special relativity was essentially the change from the invariance (symmetry) with respect to the Galilean group of transformations to the invariance with respect to the Lorentz group. The most general form of symmetry in physics is so-called CPT symmetry where C represents the transformation of charge (or transformation from matter to antimatter), P is the parity transformation (mirror reflection), and T is the change of the direction of time. The surprising fact is that the group associated with the CPT symmetry is Klein’s group.

We can find Klein’s group in the contexts of symmetry at all levels of reality. For instance, in the study of child development, Jean Piaget distinguished the so-called INRC group, that is, the Klein group [8]. Claude Levi-Strauss identified Klein’s group in the structure of the myth of several cultures [9].

The omnipresence of Klein’s group may seem mysterious. What could be the link between the CPT symmetry of physics, the mental development of children, and the structure of myths? The mystery can be dispersed when we look at the lattice of subgroups of Klein’s group. It is M₅ (Figure 1) whose presence is a criterion for the non-distributivity of lattices. Thus, the multiple occurrences of Klein’s group indicate the presence of the integrative logic of the information involved in each of the cases. It is too early to make any conclusions regarding the model of information integration mechanisms, but Klein’s group points in the direction of a likely solution.