1. Introduction
A motor vehicle crash can cause considerable economic loss, serious bodily injuries and loss of human life. Crash scene investigation and reconstruction are considered crucial being part of the major concerns in traffic incident management (TIM) [
1]. Traditional coordinate and triangulation methods have long been adopted by investigators at a crash scene. They use mechanical measurement tools such as tape measures and roller wheels to acquire baseline measurements and delineate crash scene diagrams [
2]. While relatively low cost, these methods have limited efficiency to document measurements and pose safety risks to investigators due to possible exposure to traffic. In order to automate accurate documentation of distance and angle measurements, total stations have started to play a key role at crash scenes since the early 1990s [
3]. The ability to collect digital data off the roadway eases investigators’ exposure risk to traffic and reduces entire surveying time. Close-range photogrammetry, which emerged around the same time in accident investigation, is able to recover accurate two-dimensional (2D) and three-dimensional (3D) measurements and diagrams by taking overlapping photographs from different viewpoints around crash scenes [
4]. Over the past two decades, the potential of terrestrial laser scanning (TLS) has been validated in various crash scene scenarios [
5,
6,
7]. Enormous scene details can be scanned and captured in a relatively short period of time. However, the costs of TLS equipment are usually high, and multiple scan locations may be needed to minimize scan occlusions in scenes where terrain and crash are complex.
With rapid advances in microelectronics, radio communication, miniaturized imaging lenses and positioning modules, small unmanned aircraft systems (sUASs) have pioneered a series of TIM applications, such as traffic monitoring, flow analysis, crash detection and response, and situational awareness [
8,
9,
10]. Advantages of using sUAS platforms for TIM include: (1) allowing for customization of onboard sensing systems and observing parameters, (2) offering adequate flexibility in data collection above the scene to be investigated, (3) reducing the exposure of investigators to the dangers of traffic in the roadway, and (4) providing detailed 2D and/or 3D measurement documentation and imagery for post-crash scene investigation conducted in the office. Nowadays, the potential of multirotor sUASs being low-cost and robust crash scene recovery platforms has been manifested via structure-from-motion (SfM) photogrammetry. SfM converts overlapped image sequences taken by a consumer-grade digital camera into 2D orthorectified image products and reconstructed 3D scenes (dense 3D point cloud data and textured 3D meshes). SfM photogrammetry with an octocopter platform was reported to save up to 90% of data collection time compared with traditional coordinate method [
11]. Measurements obtained from the point cloud were in accordance with sketches drawn by the investigators, and centimeter-level differences were found in the entire scene. Above the accident scene, orthophotos can be generated using a sequence of individual photos converted from the 4 K-resolution video taken by the quadcopter camera [
12]. The results demonstrated a horizontal accuracy of 5–8 cm in scene documentation compared with a real time kinematic (RTK) global navigation satellite system (GNSS) survey.
While growing attention has been paid to SfM photogrammetric surveys with sUAS platforms in crash scene investigation and recovery, it is important to realize that nearly 21% of the crashes are weather-related every year in the United States [
13] and performing flight missions under hazardous weather conditions remains a difficult task due to safety and data quality concerns. For example, wind is a frequent natural phenomenon, but high winds tend to increase the risks of freight truck crashes on the roadway [
14,
15]. In such a scenario, before an sUAS is dispatched to conduct the crash scene reconstruction mission, it is essential to ensure that the wind speed does not exceed the aircraft’s operation limit specified by the vendor. Some sUASs are less susceptible to the wind disturbance, but their battery life and flight time is reduced as wind speeds increase [
16,
17]. High wind speed can also negatively affect the SfM photogrammetry and derived mapping products due to disturbed waypoint targeting and image orientation. Wind direction and turbulence are also important variables to consider as they affect the flight path geometry, energy consumption and overall flight safety [
18,
19,
20,
21].
Some studies have documented preliminary findings on the variations of sUAS flight stability due to wind forces. Wang conducted an in-house simulation to assess the wind impacts on sUAS flight stability at low altitudes [
22]. The differences in flight speed and attitude were summarized when various types of wind were examined. Siqueira mathematically created a wind model and evaluated its effects on sUAS trajectory tracking by looking into 2D/3D error and control activities [
23]. The results suggested rapid trajectory tracking degradation as a response to the increased magnitude of wind dynamics.
Initial research efforts have been made in recent years to use open-source mission planning tools such as Mission Planner to conduct sUAS simulation runs in windy conditions [
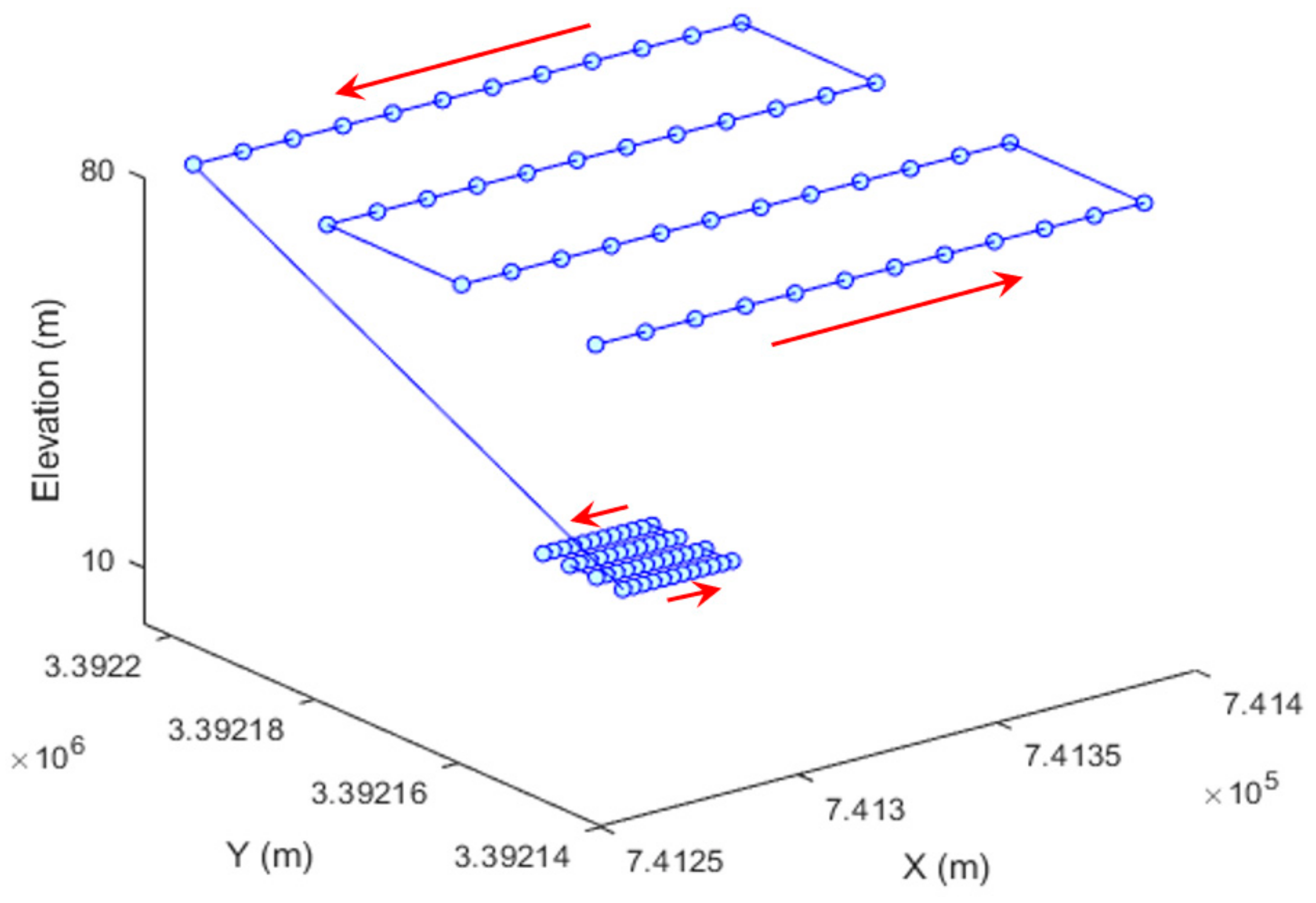
24]. However, comprehensively characterizing sUAS responses to various wind conditions has been understudied but is considered crucial before planning flight operations for crash scene reconstruction. While there are multiple types of suboptimal weather conditions that raise safety and data quality concerns for flying sUASs, the main aim of this study is to set wind as an exclusive factor to parameterize its impacts on flight performance of a representative quadcopter sUAS platform type via realistic flight simulations using a standard gridded flight design for SfM image acquisition. Simulation results are applied to document and generalize lessons learned for platform-independent quadcopter sUAS flight design under windy conditions for crash scene mapping. A series of quadcopter simulations with incremental increases in wind speed, direction, and turbulence are performed to model suboptimal weather conditions. Positional error, battery use, and flight time are used as statistical metrics to characterize the wind impacts on flight performance.
4. Lessons Learned and Conclusion
A timely investigation and reconstruction at the motor vehicle crash scene plays a pivotal role in identifying the cause and severity of the accident, assessing roadway safety risks, clarifying insurance liabilities, and facilitating legal proceedings. SfM photogrammetry with sUAS in crash scene reconstruction has gained increasing attention in recent years because of its reliability and flexibility in offering quality geospatial surveying products. One of the main deficiencies in past literature has been the failure of demonstrating its effectiveness in adverse weather conditions, under which the risk of motor vehicle crashes is exacerbated. In this article, wind was chosen as the primary factor that drove adverse weather conditions, and the sUAS was presented in the form of a simulated quadcopter in the ArduPilot SITL environment. The main objectives were to: (1) characterize the impacts of wind speed, direction, and turbulence on the positional accuracy, required flight time, and battery use of the simulated quadcopter type via realistic flight simulations, and (2) generalize lessons learned for platform-independent quadcopter flight design under wind conditions for crash scene mapping. Real-world quadcopters were not tested and compared due to flight safety and compliance concerns. The simulation also provided a method to assess wind impact on flight design in a systematic and controlled fashion, which is generally not feasible in real-world operating conditions. A total of 58 simulation runs with incremental increases in wind speed, direction, and turbulence were created and analyzed at a single altitude of 80 m AGL. Six more simulation runs were created and analyzed at dual altitudes of 80 m and 10 m AGL.
The wind disturbance settings were deliberately chosen to ensure that the simulated quadcopter was able to maintain the planned route and avoid divergent 3D errors between intended waypoints and actual camera trigger locations. The results indicated that as wind conditions departed from the ideal zero-speed with no-turbulence scenario, there was an adverse impact on sUAS stability performance, measured in terms of positional accuracy, required flight time, and battery use. Several lessons learned related to real-world quadcopter sUAS flight design under wind conditions for crash scene reconstruction are discussed and summarized below.
The average 3D error and corresponding standard deviation of 3D error between planned waypoints and the actual camera trigger locations increased as the wind speed increased. The research findings suggested operating the simulated quadcopter when the wind is not greater than 11 m/s. It is important to note that this ArduPilot quadcopter module has been run on real-world systems such as 3DR Solo and Parrot Bebop 2, and this conclusion accords well with the accepted wind tolerance that the respective user guides recommend for these platforms [
33,
34,
42]. This recommendation on wind tolerance is also consistent with that of other popular quadcopter sUAS platforms in current operation of similar size such as DJI Phantom 4 Pro/Pro+, DJI Inspire 2 and Skydio 2 [
43,
44,
45]. However, it should be realized that wind tolerance is platform dependent and 11 m/s as the documented value in this work may not be generalized for all types of quadcopter sUAS platforms. For the average 3D error and corresponding standard deviation of 3D error between planned waypoints and the actual camera trigger locations, the magnitude of the impact varied significantly as a function of the turbulence level. The simulation runs also demonstrated that the flight performance remained relatively stable under light to moderate turbulence levels (i.e., turbulence level ≤5).
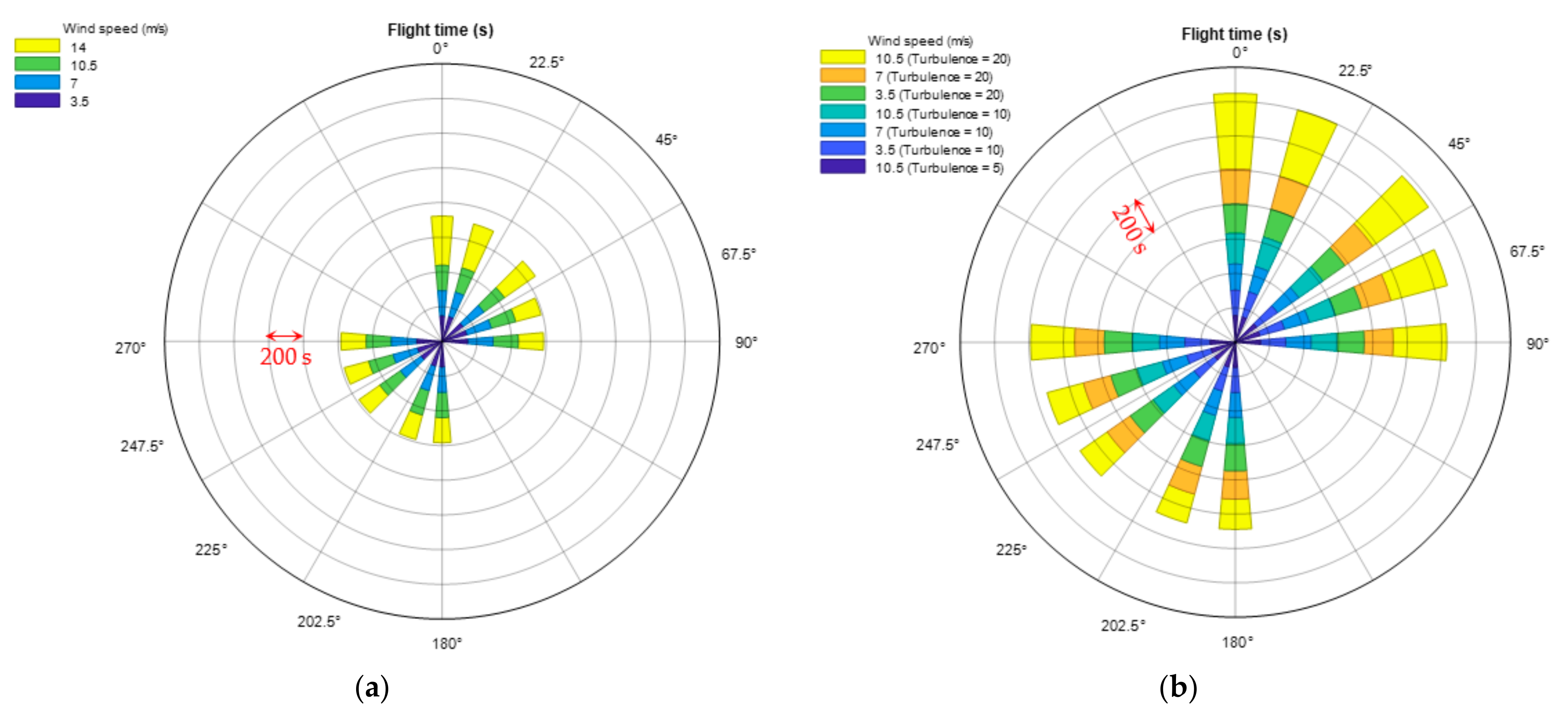
Flying perpendicular to the wind direction is a well-known practice for fixed-wing sUAS survey missions. It helps maintain stable ground speed during imagery data collection [
46,
47]. Results obtained in this study suggest that this rule of thumb for fixed-wing aircrafts applies well to quadcopter sUAS platforms. Under high wind and low turbulence scenarios (e.g., a wind speed of 14 m/s and turbulence level of 0), statistical results proved that flying in crosswind (i.e., α = 90° or 270°) and against headwind (i.e., α = 0°) were the most and least favorable flight patterns, respectively. While the average 3D error metric was not sensitive to the increase of wind speed in crosswind scenarios (i.e., α = 90° or 270°), the average 3D error sharply grew four times if wind speed rose from 0 to 14 m/s for the headwind scenario (i.e., α = 0°). Similar results were observed in the flight time metric. The sUAS spent nearly twice as much time on headwind flight segments (i.e., α = 0°) than those segments where flight lines were perpendicular to the wind direction (i.e., α = 90° or 270°). As shown in the simulation runs, the total flight time metric was less sensitive to changes in wind speed, direction, and turbulence conditions than the average 3D error and standard deviation metrics. The ideal flight paths for quadcopter sUAS platforms are, therefore, supposed to stay nearly perpendicular to horizontal wind. However, in real-world scenarios, this goal may not be achievable in every single flight attempt due to road geometry at the crash location, overhead safety concerns, airspace restrictions and so forth. A general recommendation to the crash investigation team and sUAS remote pilot within high wind and low turbulence environments is to apply this conclusion when pertinent on-site conditions permit.
Under strong wind conditions (e.g., wind speed ≥ 11 m/s and turbulence level >5 for the simulated quadcopter platform in ArduPilot SITL), flight stability degraded dramatically, resulting in disrupted frontal and side overlap settings due to large waypoint targeting errors. This overlap disruption is expected to get amplified for flight missions at a low altitude (e.g., below 10 m AGL) due to smaller camera field of view (FOV). This can result in a decreased number of detected and matched features in a pair of overlapping images in SfM processing routine, potentially affecting the overall quality of 2D orthomosaic image and 3D point cloud products. Even if overlaps are not disrupted in some cases, remote pilots are supposed to take battery usage into careful consideration prior to conducting high-wind flight missions. Nowadays, many commercially available multirotor sUAS platforms need a 2S to 6S lithium-ion polymer (LiPo) battery with the energy capacity less than 6000 mAh to achieve best balance between performance, flight time, and weight [
43,
44,
45,
48,
49]. Assuming this battery specification applies to the examined quadcopter platform in ArduPilot SITL,
Table 10 implies that when strong wind and turbulence exist (i.e., wind speed of 10.5 m/s and turbulence level of 20), the fully charged LiPo battery can potentially run out of power before completion of the mapping mission over the simulated crash scene area of 105 × 70 m. The rapid degradation in flight efficiency as observed from the simulation runs and platform demonstrates the need for adequate battery backup under high wind conditions, even when the scene is within a limited geographic extent. However, while this statement is generalized, it needs to be pointed out that battery consumption is platform dependent. Some lighter weight quadcopters may potentially complete a mission with one LiPo battery should they withstand as much wind as the simulated quadcopter type.
At a crash scene, the quadcopter to be deployed on the ground usually stay in close proximity to the on-site investigators and nearby vehicles. If the wind speed is marginally below the aforementioned maximum wind tolerance (e.g., 11 m/s for the simulated quadcopter in ArduPilot SITL), the remote pilot is supposed to pay extra attention during quadcopter take-off and landing phases. This is because a quadcopter sUAS is likely more susceptible to the air movement when it is flat on the ground and sitting still, causing an increased risk of flipping over in windy conditions. When the platform comes to hover in the air or traverse pre-defined waypoints to collect images for a photogrammetric survey, it should largely be able to withstand the maximum wind tolerance in a relatively steady state. In such phase, the gimbal stabilizer, which is nowadays attached to many commercially available quadcopter sUAS platforms, also helps maintain favorable image quality by compensating for angular motions to the onboard camera.
It is worth emphasizing that as a popular and reliable open-source autopilot software suite, ArduPilot has been used on a wide spectrum of autonomous systems with full-featured autonomous capabilities. ArduPilot on SITL features a high-fidelity simulation environment running a realistic flight dynamics model, and therefore, the major simulation findings summarized in this study are expected to be applicable to real-world flight scenarios. In addition, the choice of 80 m and 10 m AGL in the article was generic. Changing flight altitude did not vary wind and turbulence effect and hence, did not affect the simulated results other than flight endurance and battery consumption. The wind and turbulence parameters were defined and adjusted in Mission Planner interface, so the same wind impact results apply to other pre-defined flight altitude for the simulated quadcopter without loss of generality. However, in a real-world flight mission for crash scene reconstruction, flight height is usually determined by considering factors such as desired GSD and camera model settings, flight time, geographic extent of the mission, and waypoint geometry given specific overlap settings.
In the United States, public and commercial sUAS operations within the national airspace system (NAS) require obtaining either a Certificate of Waiver or Authorization (COA), with the option of including a Section 333 exemption, or Part 107 license from the Federal Aviation Administration (FAA). For public safety and transportation agencies that administer auto crash investigation, having a COA may warrant sUAS operations across vast airspace regions. More importantly, the COA may grant these agencies privilege of flying in suboptimal flight conditions, such as during nighttime and foggy hours to carry out an emergency survey immediately after a crash takes place. On the other hand, getting a Part 107 license usually requires less time and effort, but it is generally considered more restrictive in various dimensions compared with the COA. Thanks to the FAA’s recent efforts, waivers to Part 107 rules can be applied to gain approvals of certain sUAS operations outside the limitations defined in the rules [
50]. For example, a waiver can request easing the restrictions of conducting routine sUAS operations above standard Part 107 flight height limits (e.g., 121.9 m (400 ft) AGL at the time of this writing). This type of special permission allows pilots of public safety and transportation agencies to operate sUASs with adequate flexibility at a crash scene while ensuring safety and compliance. Recently, the FAA provided rule amendments to Part 107 to enable routine operations of sUAS over people, from moving vehicles, and at night under certain conditions. Nowadays, sUASs have become an integral part of our daily life, and technologies to advance sUAS safety evolve rapidly. This leaves open the possibilities of exploring impacts of multiple suboptimal weather conditions on sUAS flight performance for crash scene reconstruction in the near future. The intended future work also includes: 1) investigating wind impacts on fixed-wing sUAS platforms, and 2) conducting real-world flight missions with different commercially available quadcopters under varying wind conditions and assessing the flight performance as well as SfM photogrammetric products.