An Autonomous Control Framework of Unmanned Helicopter Operations for Low-Altitude Flight in Mountainous Terrains
Abstract
:1. Introduction
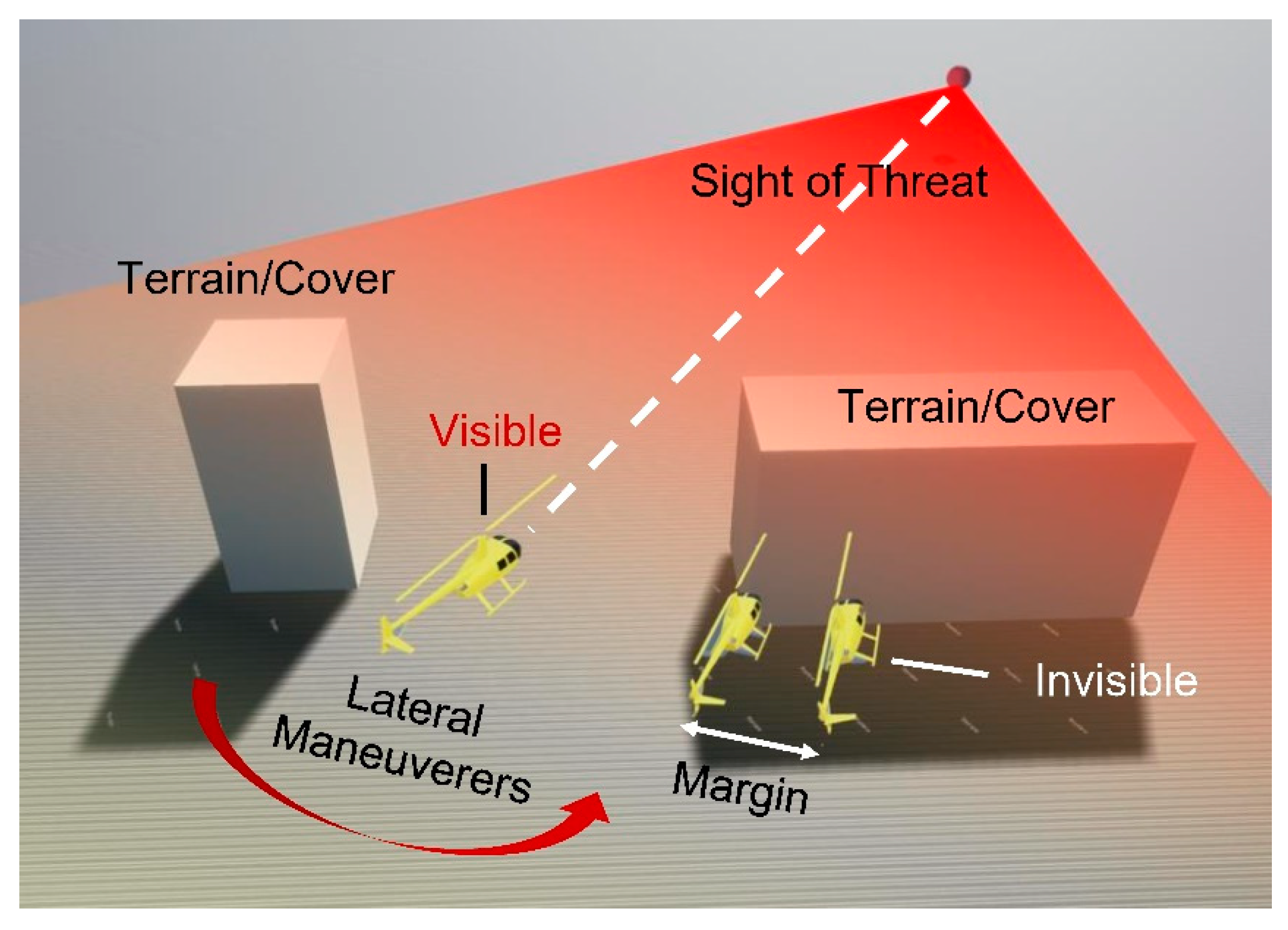
- The helicopter visibility with respect to ground threats or specific facilities is investigated in this research, which was rarely studied in previous studies about threat avoidance or survivability assessment [55,56]. We also propose a direct viewing method to judge and change the visibility quickly and robustly.
- On the basis of the visibility judgement, an integrated control framework is established using the finite state machine. Compared with many existing studies [13,19,40,47,57], this framework focuses on solving complex multi-objective flight tasks and realizing unmanned helicopter operations of cover concealment and circuitous flight similar to human pilots.
2. Problem Formulation
2.1. Low-Altitude Flight in Complex Mountainous Terrains
- Terrain following: flight maneuvering with the terrain contour in the vertical plane according to the predetermined minimum ground clearance. This penetration method can use terrain cover and reach the destination in a short time.
- Terrain avoidance: flight maneuvering in the azimuth plane, flying around mountains and other tall obstacles. This penetration method can make full use of the terrain as cover and facilitate hiding, but increases the likelihood of colliding with terrain obstacles.
- Threat avoidance: flight maneuvering in the azimuth plane, avoiding detection and weapon attacks, fully approaching the target, realizing sudden attacks, and reducing enemy interference.
- Target/threat recognition: identifying the target/threat facilities during the flight and determining the threat degrees; making maneuvering decisions on the basis of the recognition result.
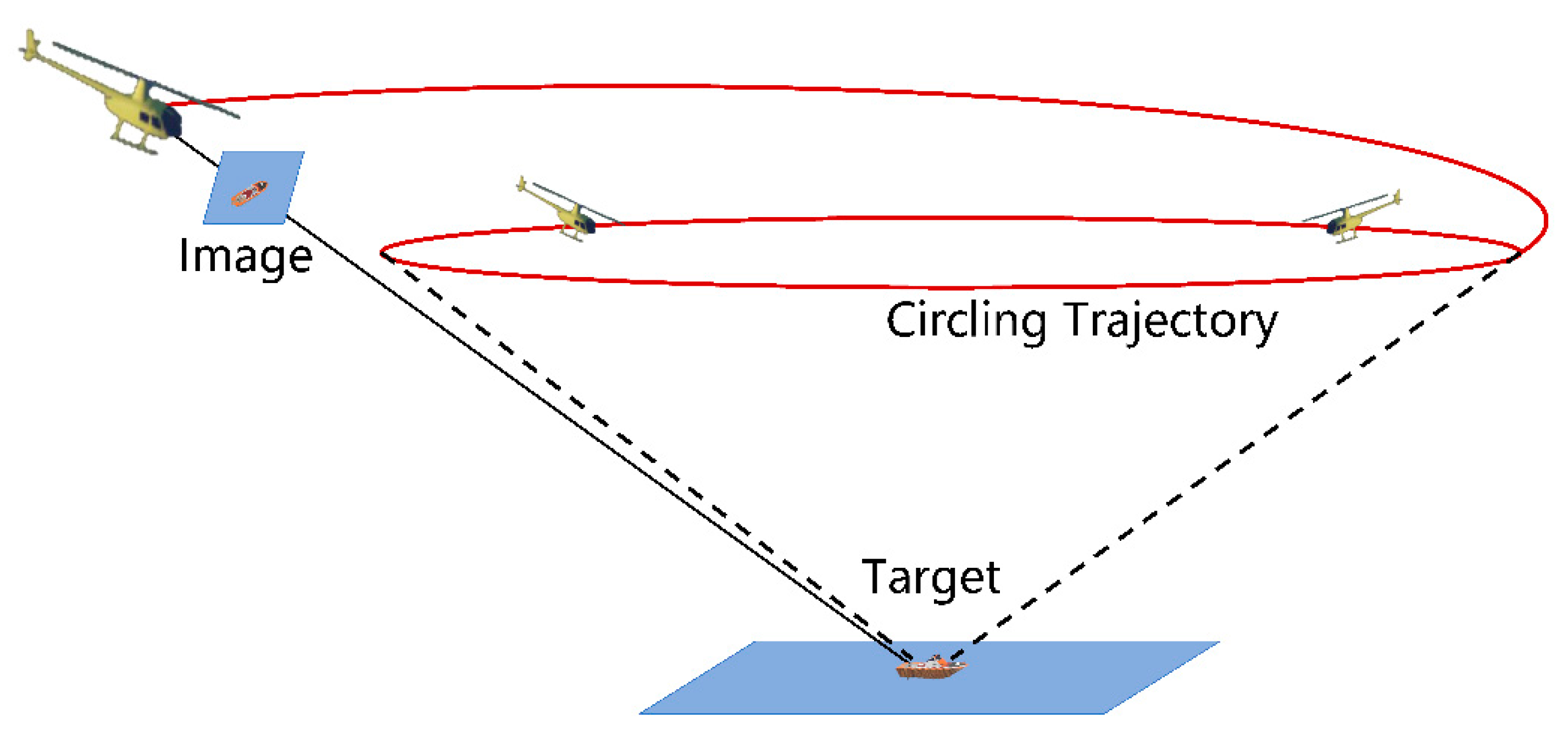
- Target approaching: identifying the target using airborne cameras, tracking and approaching the target through visual servo control, avoiding terrain obstacles, and maintaining the ability to approach the target when it is blocked or temporarily lost.
- Cover concealment: when a threat is detected, finding cover through the terrains and moving to the terrain cover to escape the threat; discriminating and changing the helicopter’s visibility through flight maneuvers.
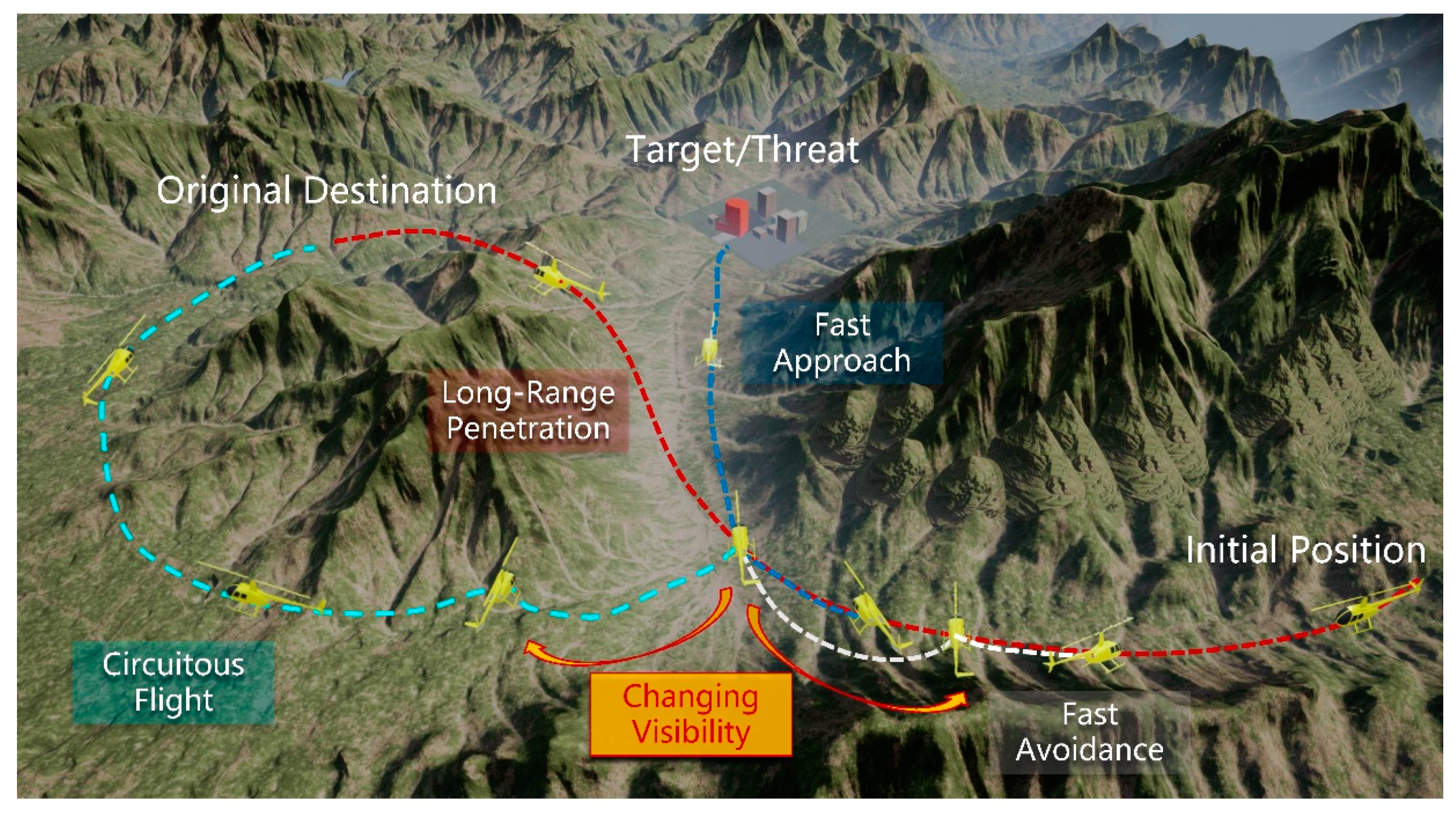
- Circuitous flight: comprehensive flight maneuvering around the terrain, avoiding the threat, and following the terrain contour near the predetermined heading, so as to finally reach the destination safely.
2.2. Modeling Method of the Simulation Environment
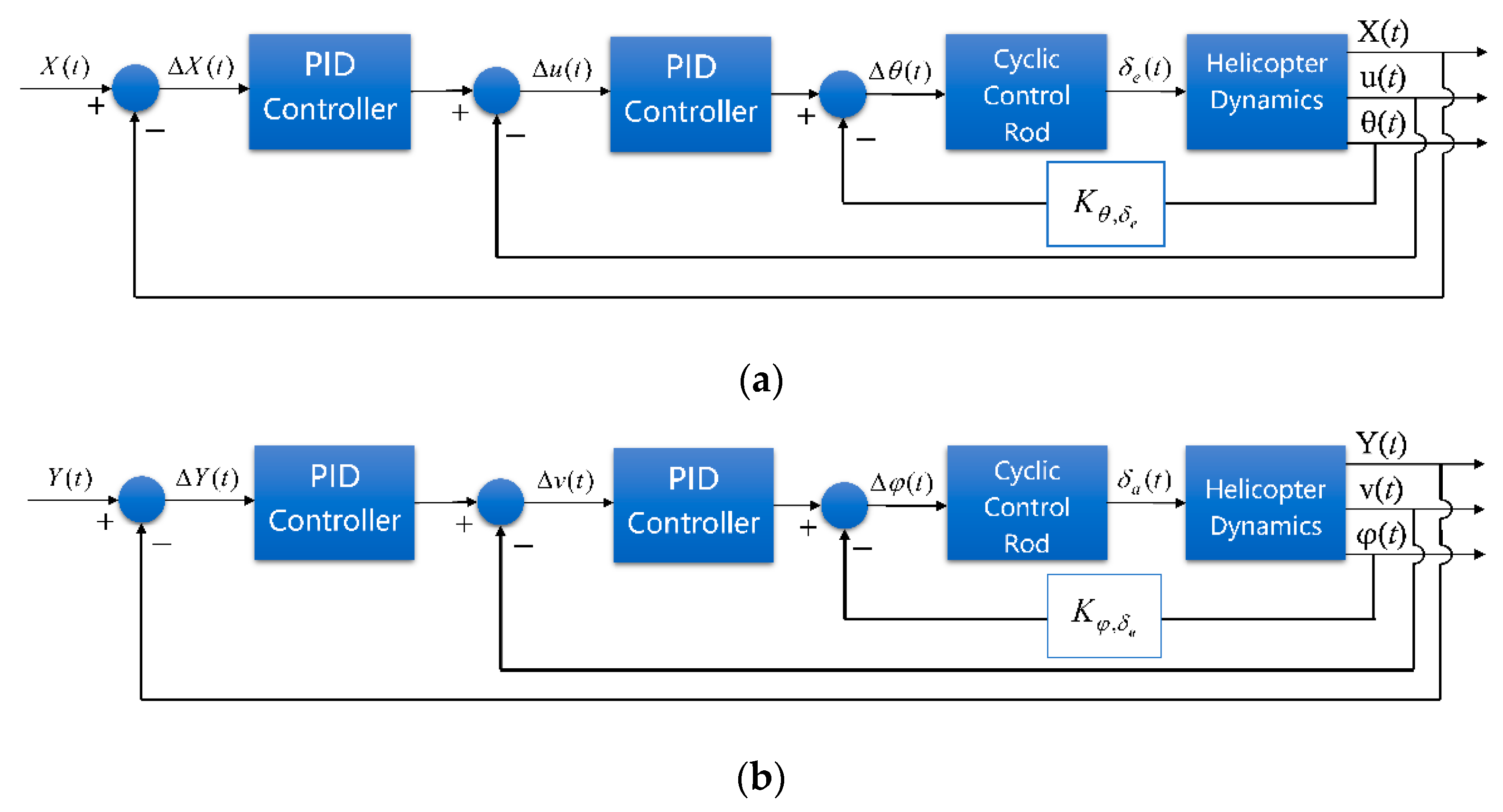
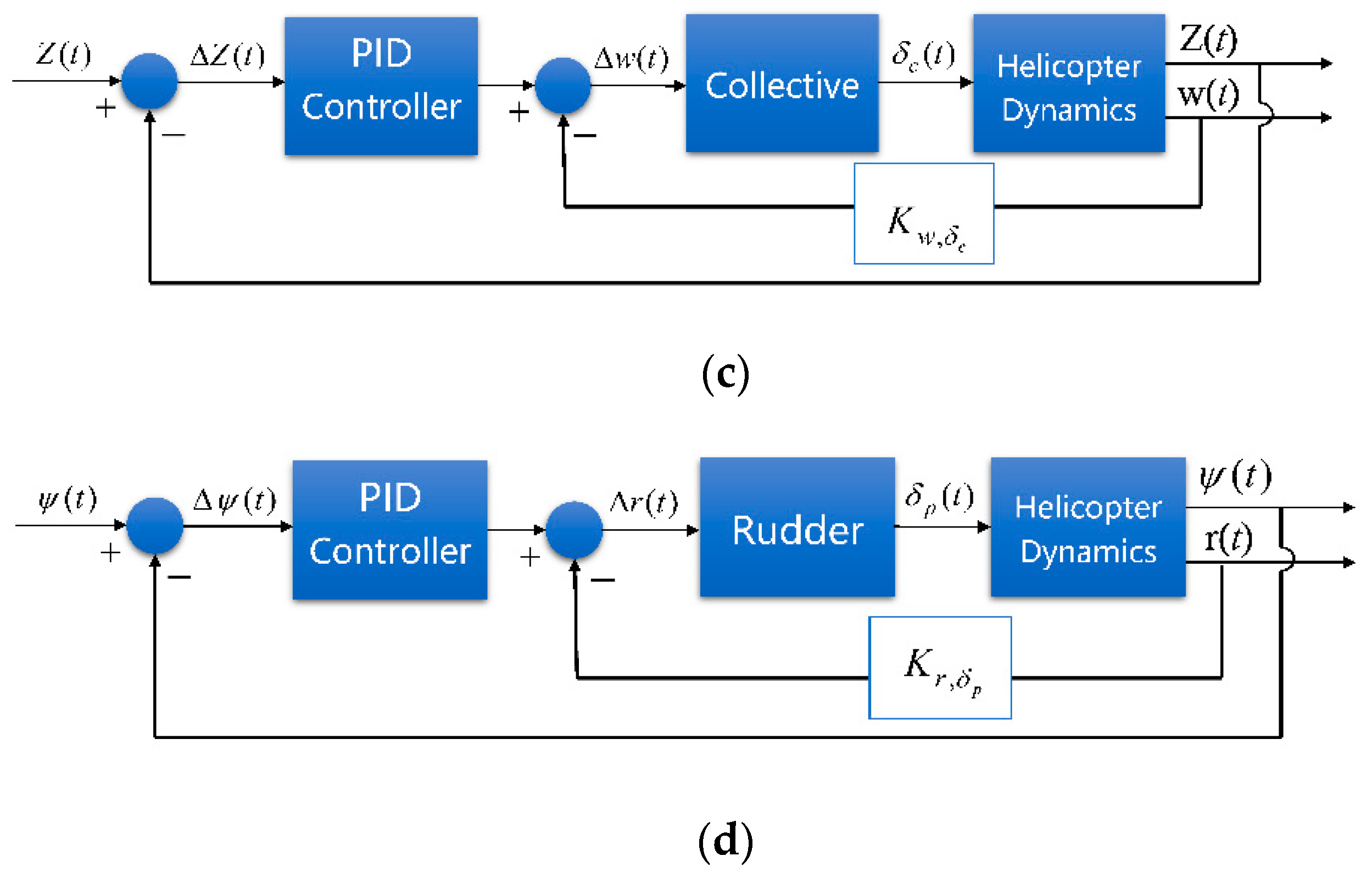
3. Target Tracking and Terrain Avoidance
3.1. Target Tracking
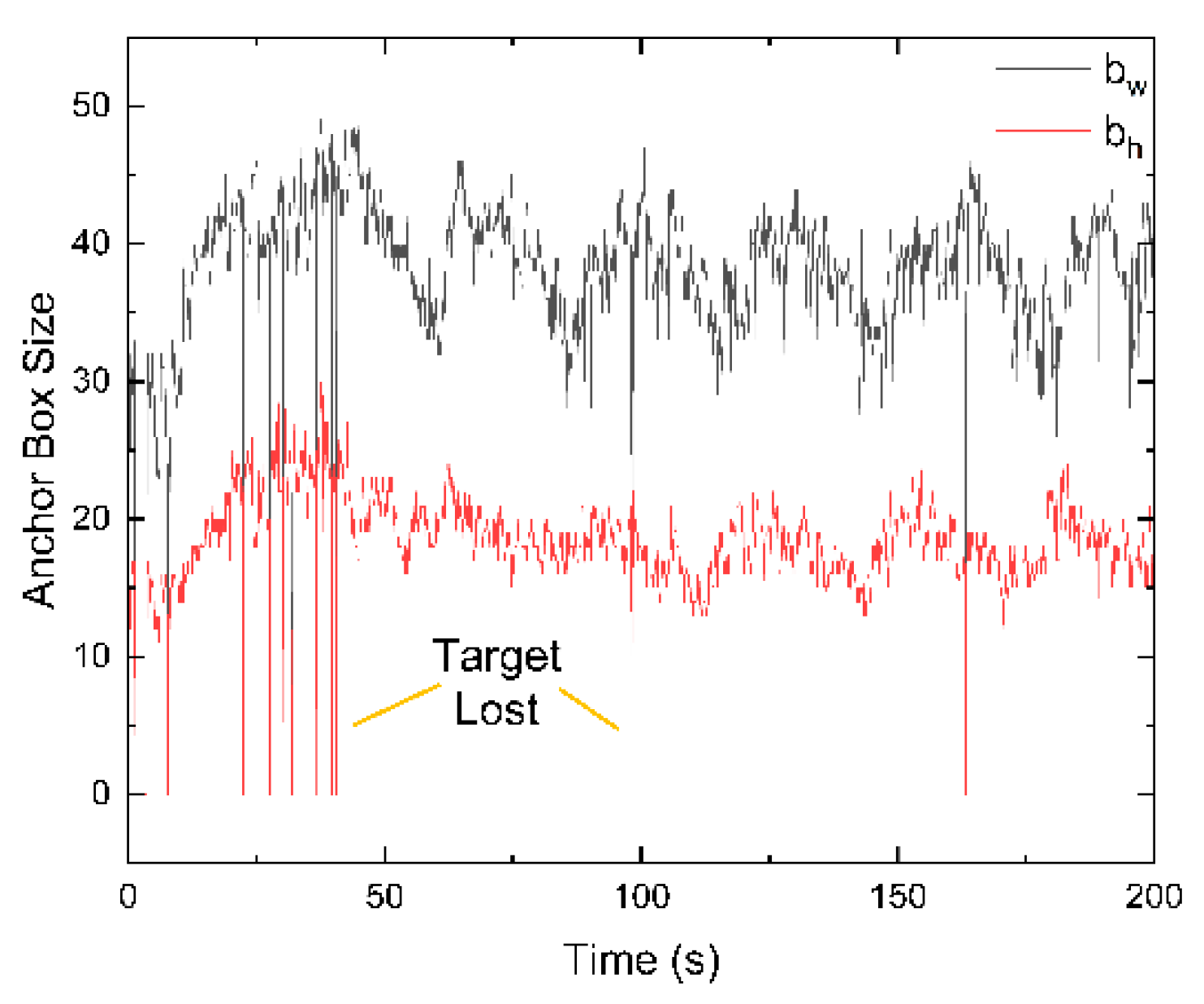
3.1.1. Target Recognition
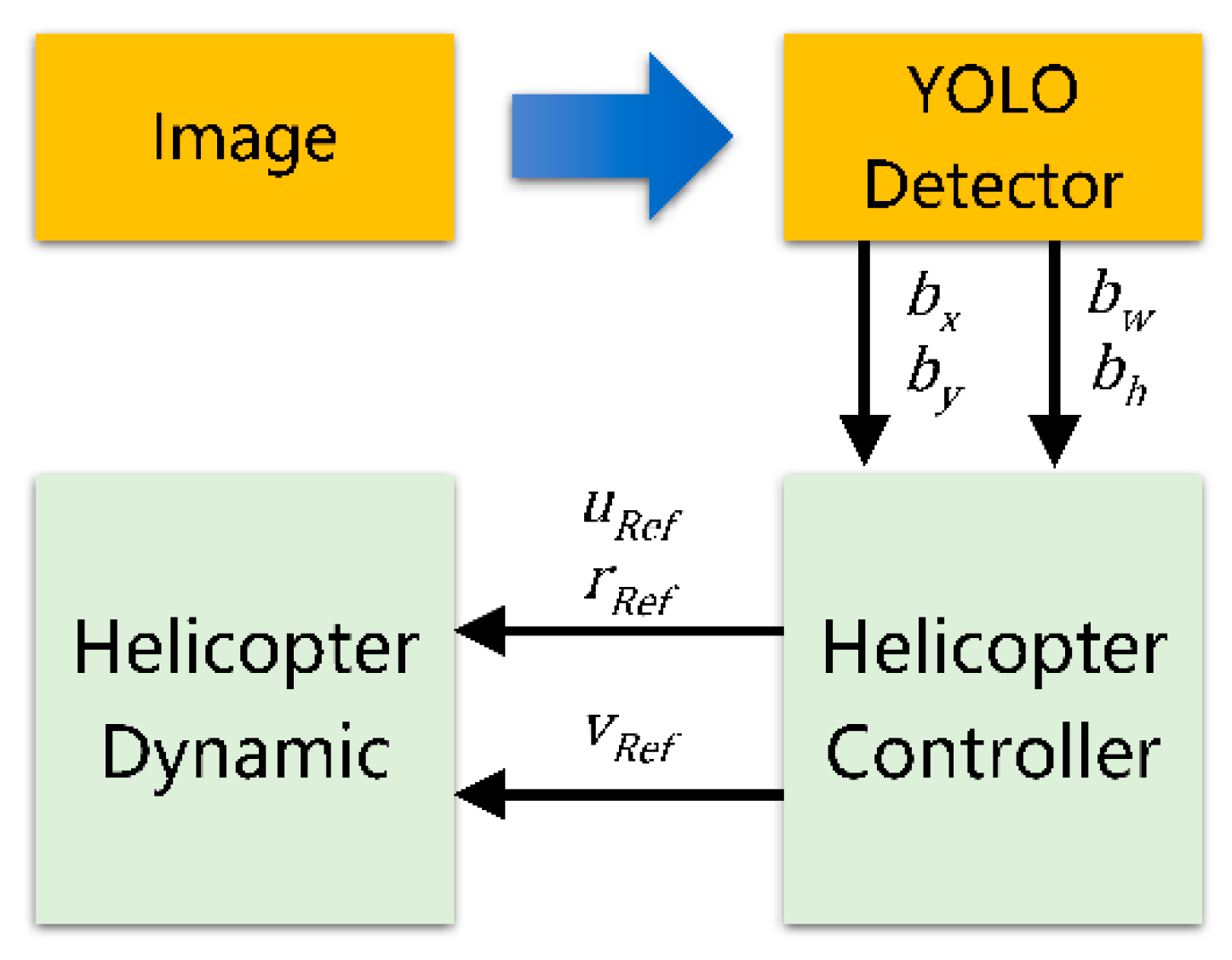
3.1.2. Visual Servo Control
3.2. Terrain Avoidance
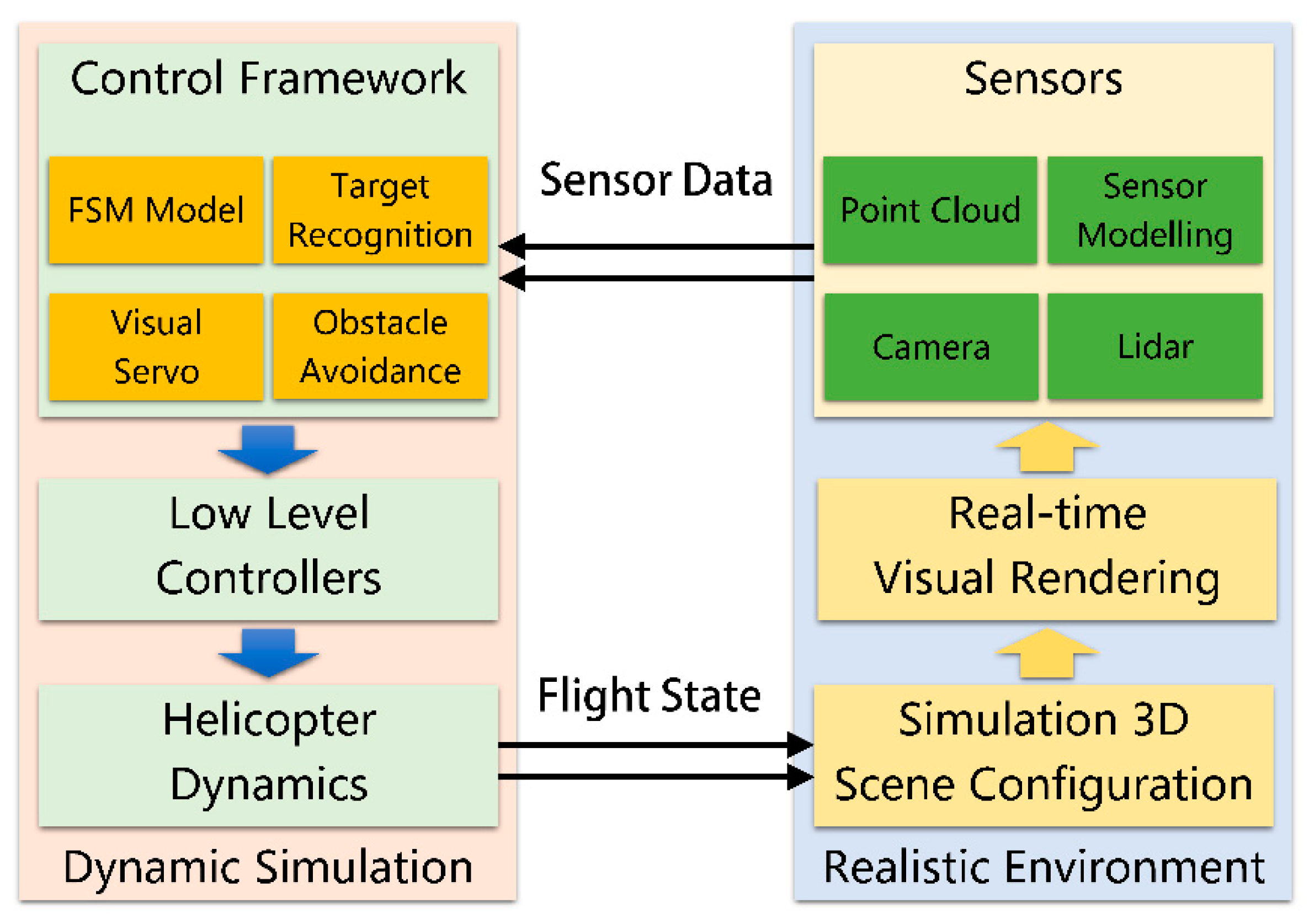
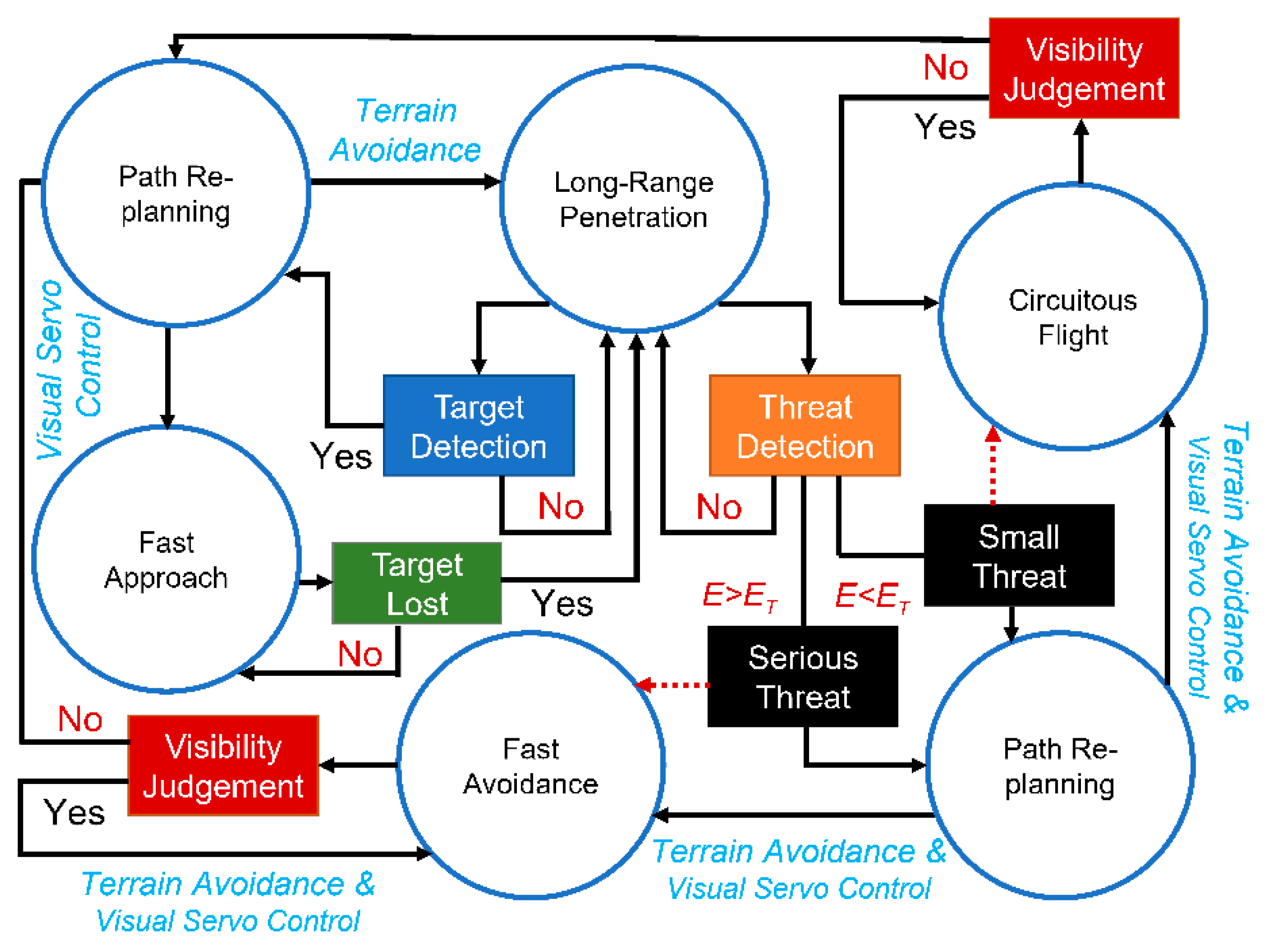
4. Autonomous Decision-Making Framework
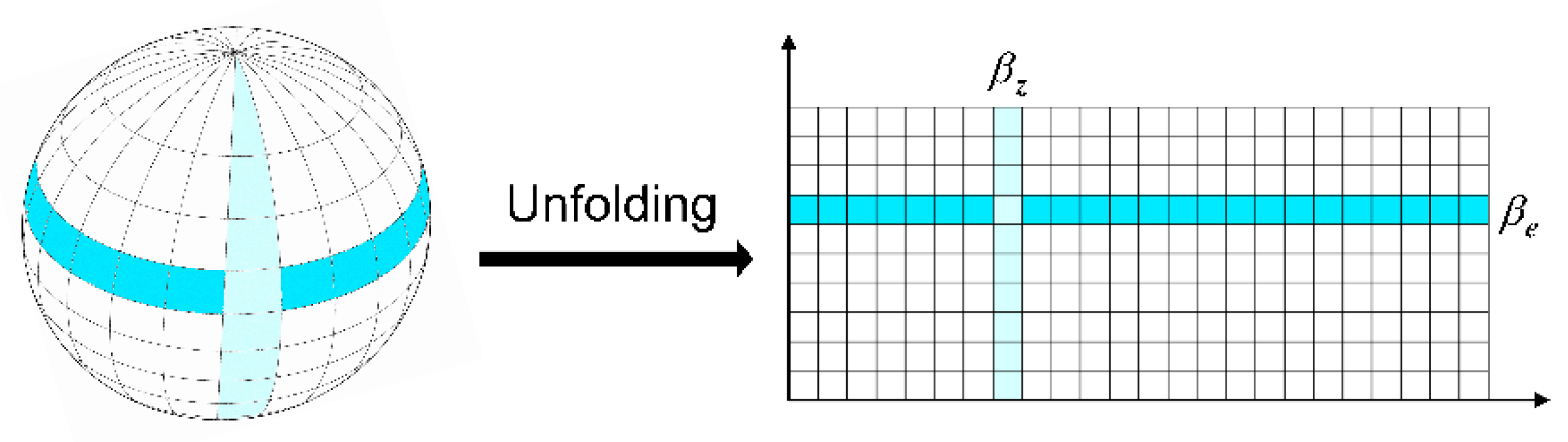
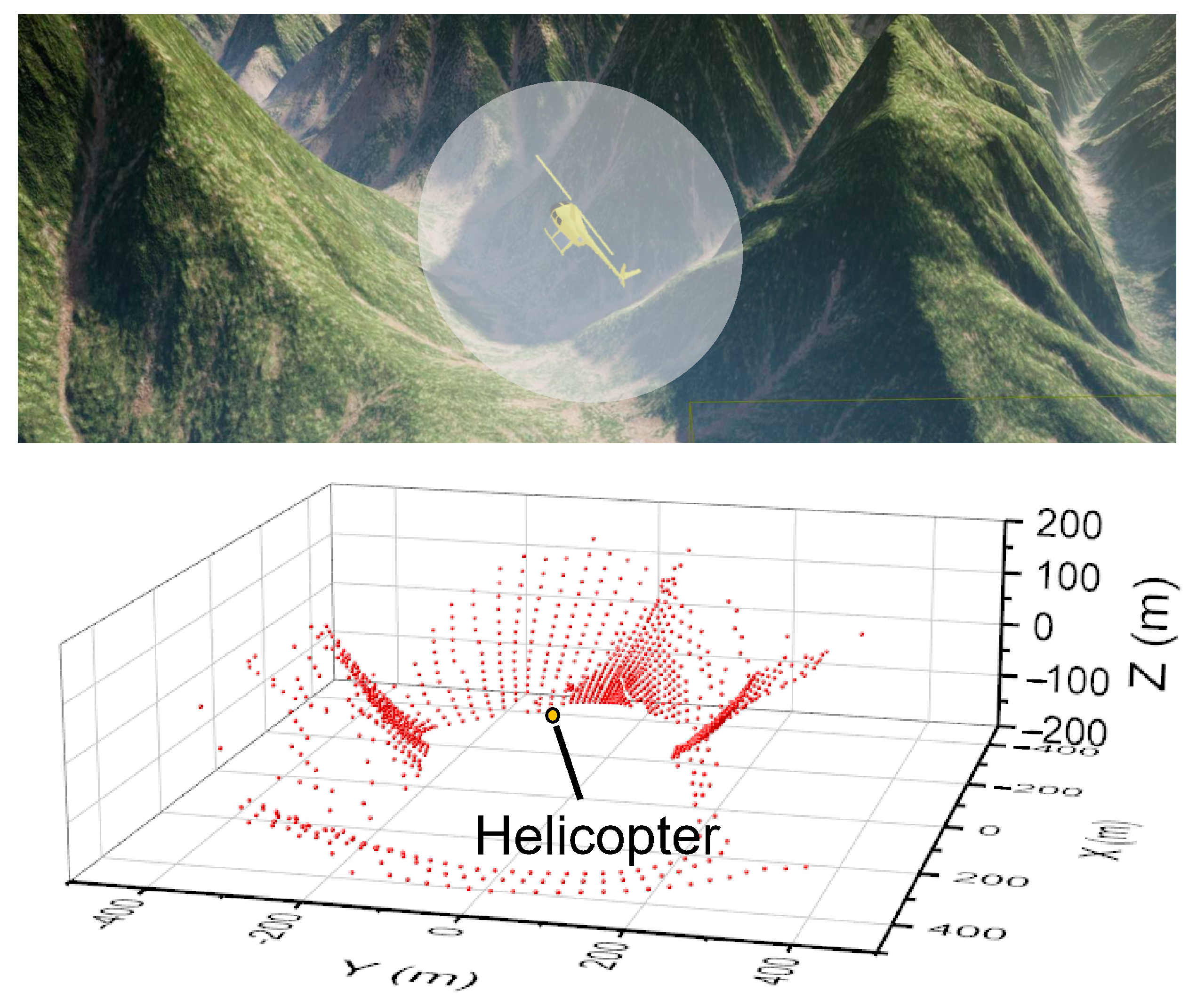
4.1. Visibility Judgment
4.2. Finite State Machine
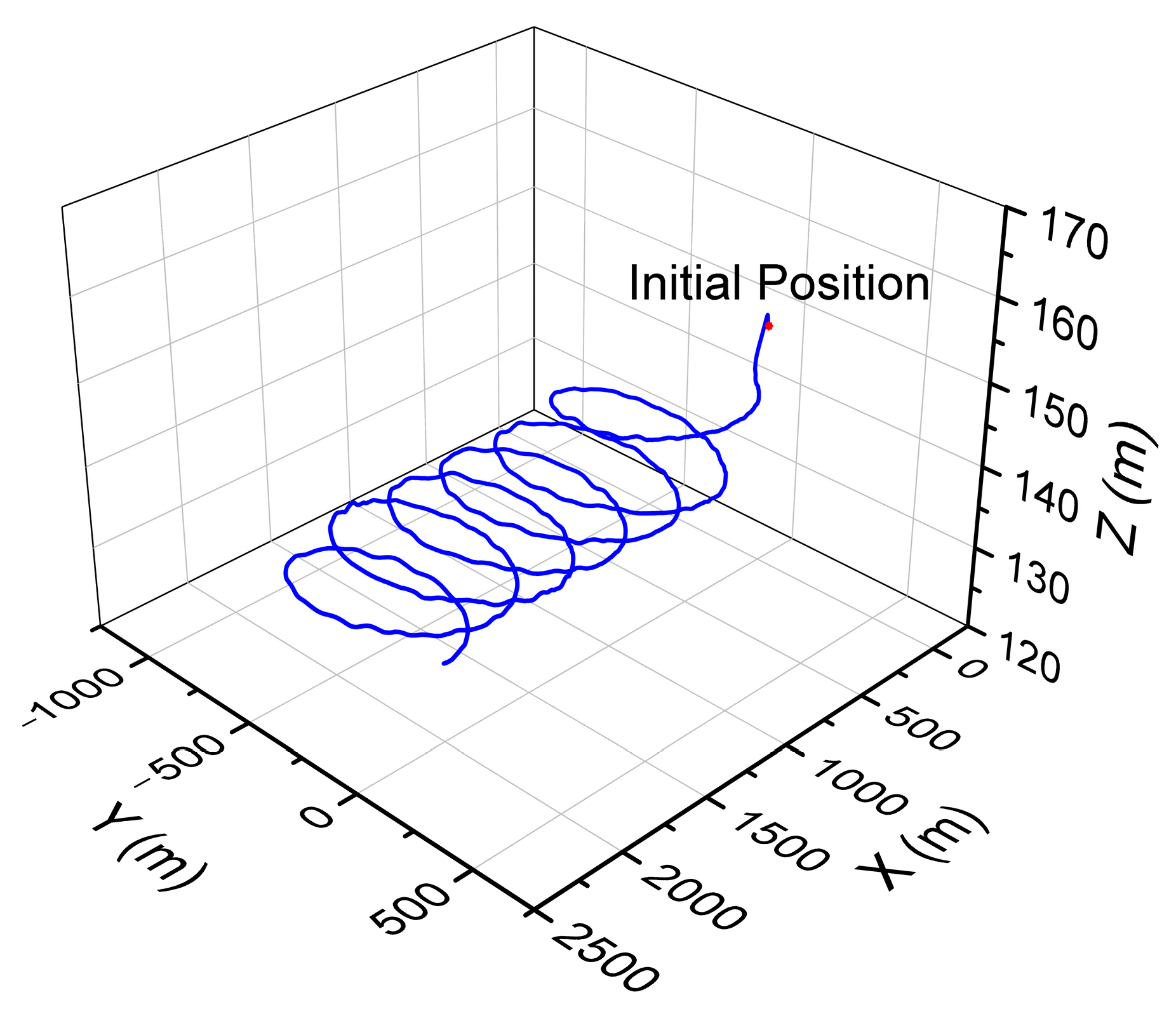
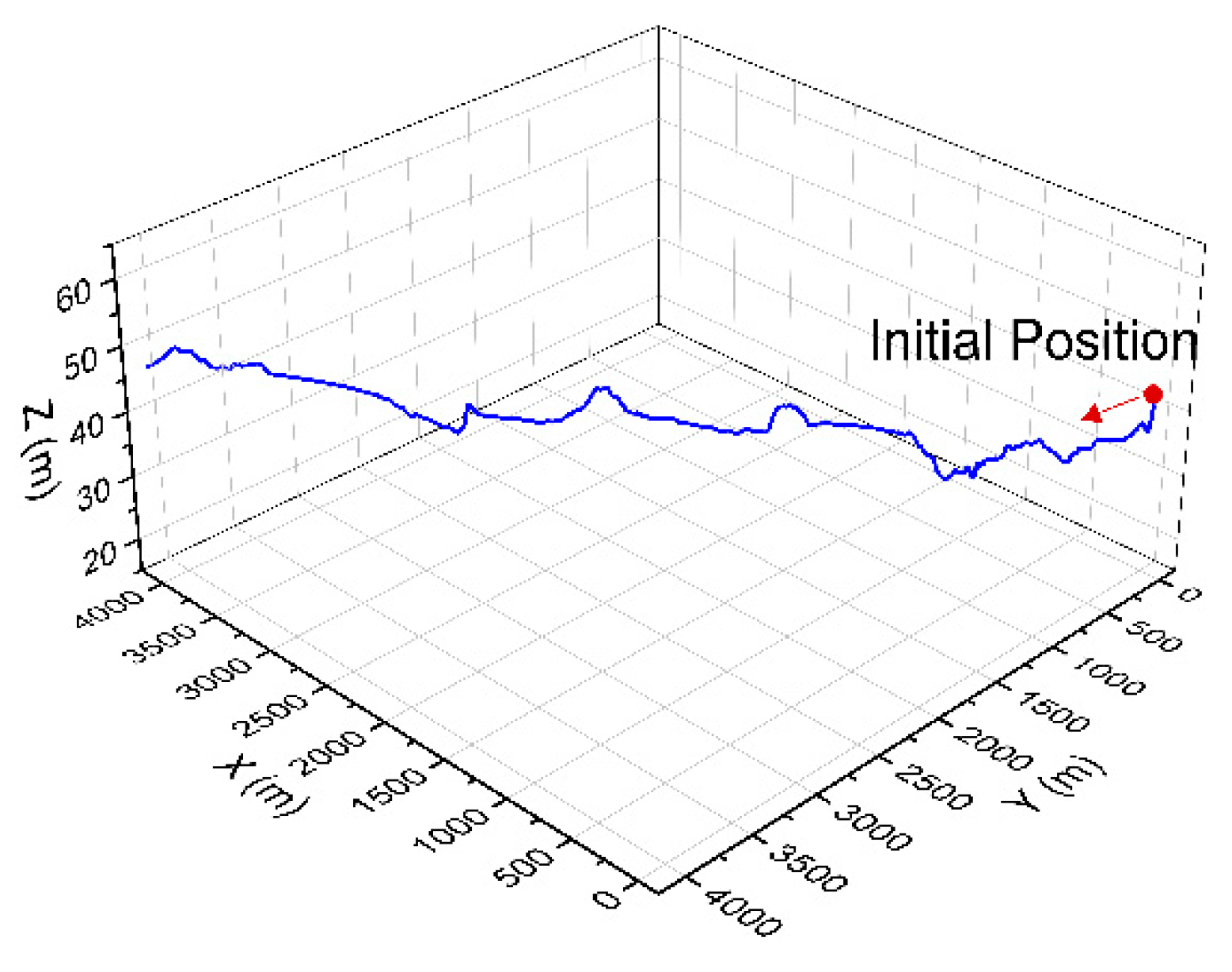
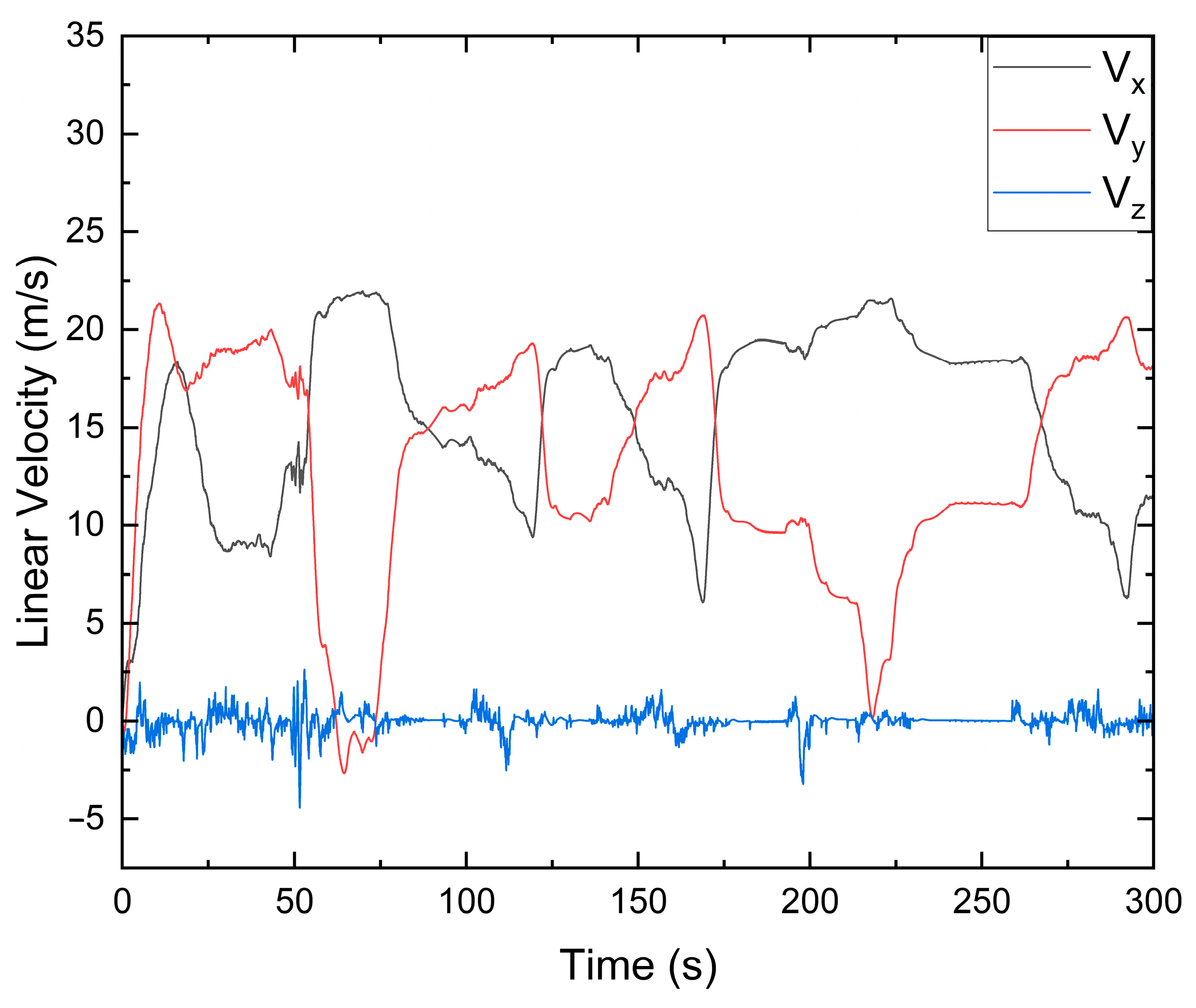
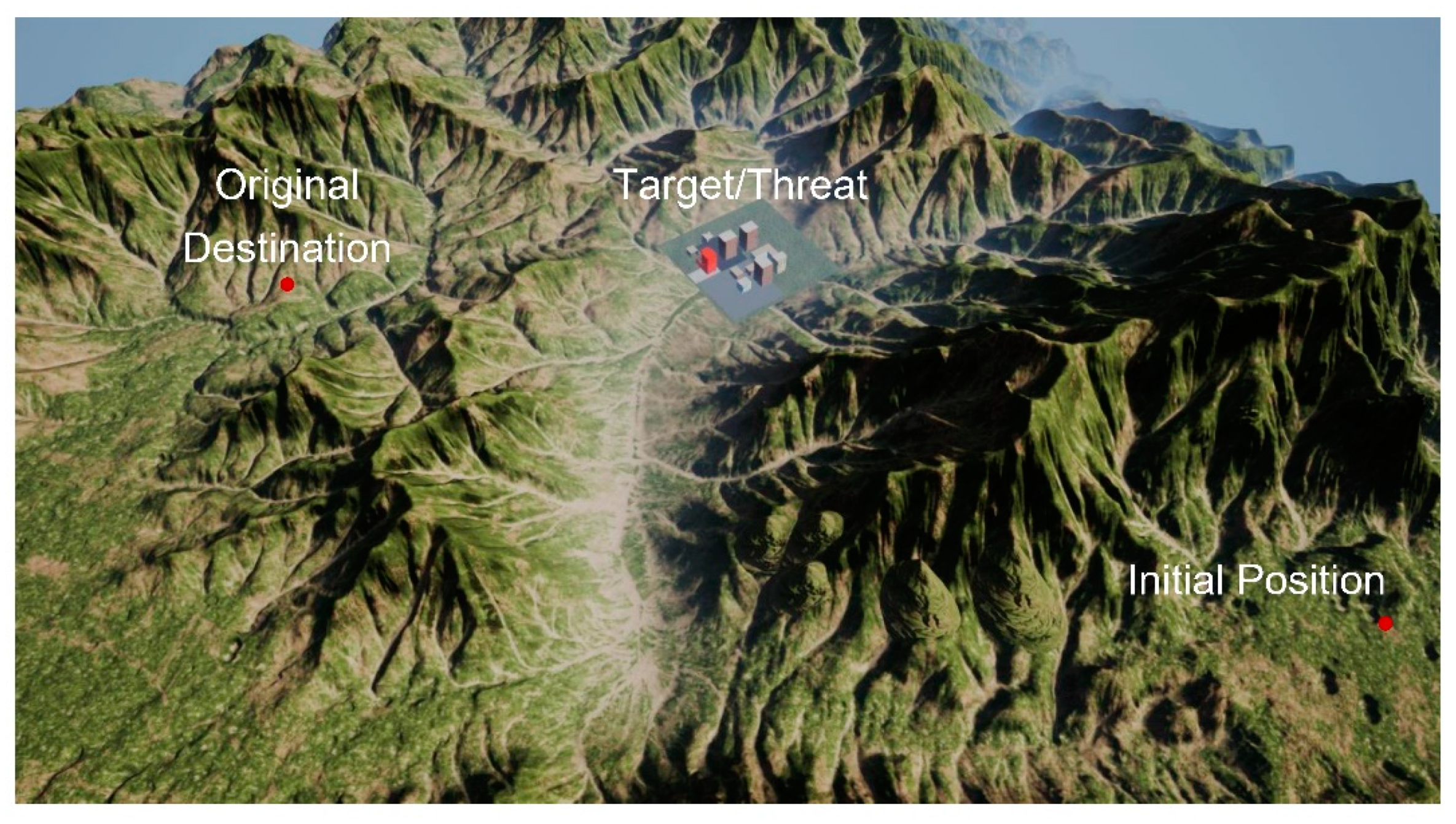
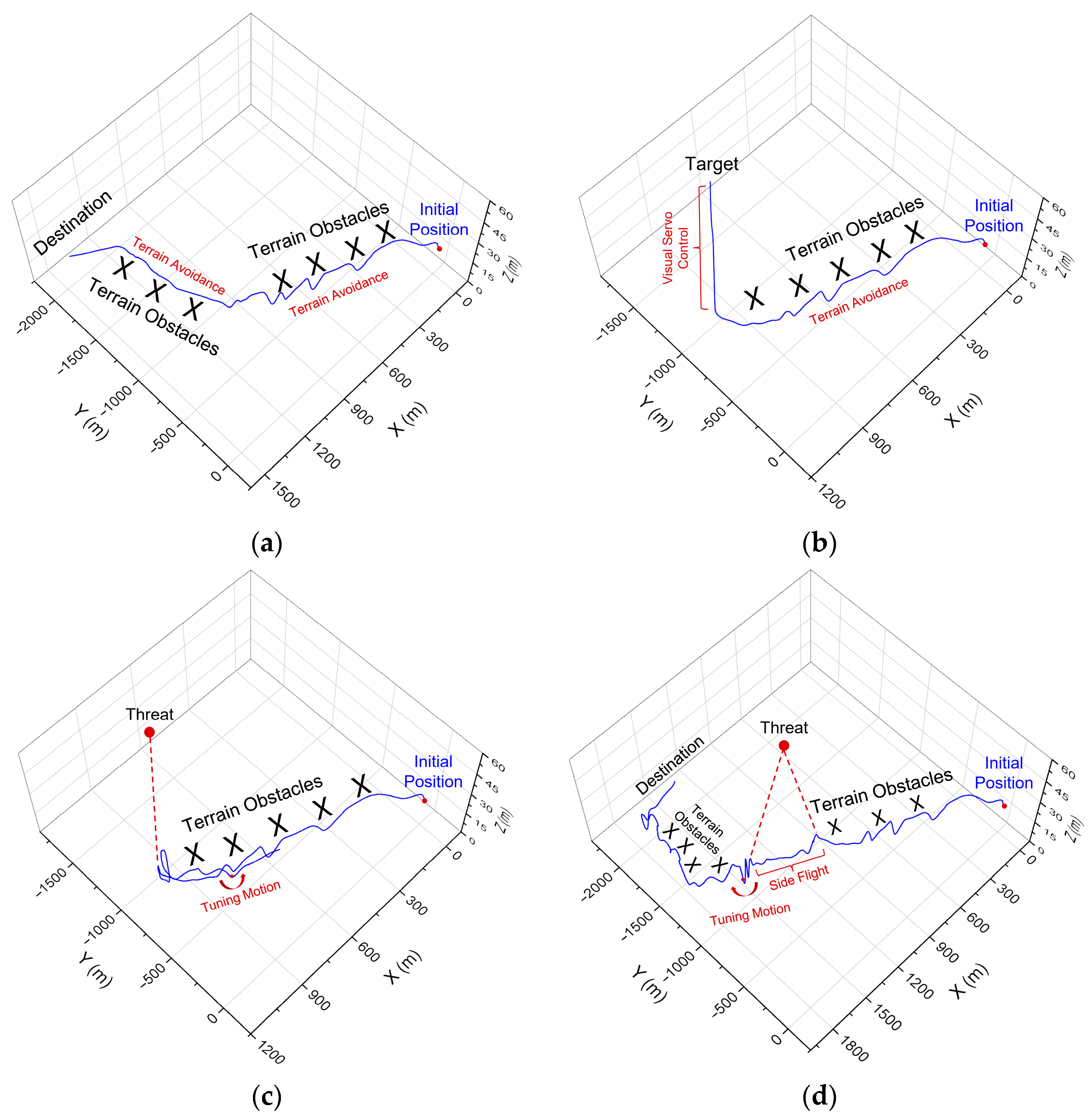
5. Simulation Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassan, S.; Ali, A.; Rafic, Y. A survey on quadrotors: Configurations, modeling and identification, control, collision avoidance, fault diagnosis and tolerant control. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 14–33. [Google Scholar]
- Lee, H.; Kim, H.J. Trajectory tracking control of multirotors from modelling to experiments: A survey. Int. J. Control Autom. Syst. 2016, 15, 281–292. [Google Scholar] [CrossRef]
- Yang, H.; Lee, Y.; Jeon, S.Y.; Lee, D. Multi-rotor drone tutorial: Systems, mechanics, control and state estimation. Intell. Serv. Robot. 2017, 10, 79–93. [Google Scholar] [CrossRef]
- Nascimento, T.P.; Saska, M. Position and attitude control of multi-rotor aerial vehicles: A survey. Annu. Rev. Control 2019, 48, 129–146. [Google Scholar] [CrossRef]
- Skowron, M.; Chmielowiec, W.; Glowacka, K.; Krupa, M.; Srebro, A. Sense and avoid for small unmanned aircraft systems: Research on methods and best practices. Proc. Inst. Mech. Eng. 2019, 233, 6044–6062. [Google Scholar] [CrossRef]
- Lin, Y.; Gao, F.; Qin, T.; Gao, W.; Liu, T.; Wu, W.; Yang, Z.; Shen, S. Autonomous aerial navigation using monocular visual-inertial fusion. J. Field Robot. 2018, 35, 23–51. [Google Scholar] [CrossRef]
- Faessler, M.; Fontana, F.; Forster, C.; Mueggler, E.; Pizzoli, M.; Scaramuzza, D. Autonomous, Vision-based Flight and Live Dense 3D Mapping with a Quadrotor Micro Aerial Vehicle. J. Field Robot. 2015, 33, 431–450. [Google Scholar] [CrossRef]
- Doukhi, O.; Lee, D.J. Deep Reinforcement Learning for End-to-End Local Motion Planning of Autonomous Aerial Robots in Unknown Outdoor Environments: Real-Time Flight Experiments. Sensors 2021, 21, 2534. [Google Scholar] [CrossRef]
- Zhou, Y.; Lai, S.; Cheng, H.; Hamid, M.; Chen, B.M. Towards Autonomy of Micro Aerial Vehicles in Unknown and GPS-denied Environments. IEEE Trans. Ind. Electron. 2021, 68, 7642–7651. [Google Scholar] [CrossRef]
- Jin, Z.; Li, D.; Wang, Z. Research on the Operating Mechanicals of the Helicopter Robot Pilot. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 887, p. 012022. [Google Scholar]
- Jeong, H.; Kim, J.; Shim, D.H. Development of an Optionally Piloted Vehicle using a Humanoid Robot. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Kovalev, I.V.; Voroshilova, A.A.; Karaseva, M.V. On the problem of the manned aircraft modification to UAVs. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1399, p. 055100. [Google Scholar]
- Hu, J.; Gu, H. Survey on Flight Control Technology for Large-Scale Helicopter. Int. J. Aerosp. Eng. 2017, 2017, 5309403. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhang, Y. Sense and avoid technologies with applications to unmanned aircraft systems: Review and prospects. Prog. Aerosp. Sci. 2015, 74, 152–166. [Google Scholar]
- Bijjahalli, S.; Sabatini, R.; Gardi, A. Advances in Intelligent and Autonomous Navigation Systems for small UAS. Prog. Aerosp. Sci. 2020, 115, 100617. [Google Scholar] [CrossRef]
- Marantos, P.; Karras, G.C.; Vlantis, P.; Kyriakopoulos, K.J. Vision-based Autonomous Landing Control for Unmanned Helicopters. J. Intell. Robot. Syst. 2017, 92, 145–158. [Google Scholar] [CrossRef]
- Lin, C.H.; Hsiao, F.Y.; Hsiao, F.B. Vision-Based Tracking and Position Estimation of Moving Targets for Unmanned Helicopter Systems. Asian J. Control Affil. ACPA Asian Control Profr. Assoc. 2013, 15, 1270–1283. [Google Scholar] [CrossRef]
- Lin, F.; Dong, X.; Chen, B.M.; Lum, K.Y.; Lee, T.H. A Robust Real-Time Embedded Vision System on an Unmanned Rotorcraft for Ground Target Following. IEEE Trans. Ind. Electron. 2012, 59, 1038–1049. [Google Scholar] [CrossRef]
- Yong, C.; Liu, H.L. Feature article: Overview of landmarks for autonomous, vision-based landing of unmanned helicopters. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 14–27. [Google Scholar]
- Miao, C.; Li, J. Autonomous Landing of Small Unmanned Aerial Rotorcraft Based on Monocular Vision in GPS-denied Area. IEEE/CAA J. Autom. Sin. 2015, 2, 109–114. [Google Scholar]
- Andert, F.; Adolf, F.; Goormann, L.; Dittrich, J. Autonomous Vision-Based Helicopter Flights through Obstacle Gates. J. Intell. Robot. Syst. 2009, 57, 259–280. [Google Scholar] [CrossRef]
- Marlow, S.Q.; Langelaan, J.W. Local Terrain Mapping for Obstacle Avoidance Using Monocular Vision. J. Am. Helicopter Soc. 2011, 56, 22007. [Google Scholar] [CrossRef] [Green Version]
- Hrabar, S. An evaluation of stereo and laser—Based range sensing for rotorcraft unmanned aerial vehicle obstacle avoidance. J. Field Robot. 2012, 29, 215–239. [Google Scholar] [CrossRef]
- Paul, T.; Krogstad, T.R.; Gravdahl, J.T. Modelling of UAV formation flight using 3D potential field. Simul. Model. Pract. Theory 2008, 16, 1453–1462. [Google Scholar] [CrossRef]
- Javier, G.; Gandolfo, D.C.; Salinas, L.R.; Claudio, R.; Ricardo, C. Multi-objective control for cooperative payload transport with rotorcraft UAVs. ISA Trans. 2018, 80, 481–502. [Google Scholar]
- Gimenez, J.; Salinas, L.R.; Gandolfo, D.C.; Rosales, C.D.; Carelli, R. Control for cooperative transport of a bar-shaped payload with rotorcraft UAVs including a landing stage on mobile robots. Int. J. Syst. Sci. 2020, 51, 3378–3392. [Google Scholar] [CrossRef]
- Watson, N.A.; Owen, I.; White, M.D. Piloted Flight Simulation of Helicopter Recovery to the Queen Elizabeth Class Aircraft Carrier. J. Aircr. 2020, 57, 742–760. [Google Scholar] [CrossRef]
- Topczewski, S.; Narkiewicz, J.; Bibik, P. Helicopter Control During Landing on a Moving Confined Platform. IEEE Access 2020, 8, 107315–107325. [Google Scholar] [CrossRef]
- Ngo, T.D.; Sultan, C. Variable Horizon Model Predictive Control for Helicopter Landing on Moving Decks. J. Guid. Control Dyn. 2021, 45, 774–780. [Google Scholar] [CrossRef]
- Zhao, S.; Hu, Z.; Yin, M.; Ang, K.Z.; Liu, P.; Wang, F.; Dong, X.; Lin, F.; Chen, B.M.; Lee, T.H. A Robust Real-Time Vision System for Autonomous Cargo Transfer by an Unmanned Helicopter. IEEE Trans. Ind. Electron. 2014, 62, 1210–1219. [Google Scholar] [CrossRef]
- Truong, Q.H.; Rakotomamonjy, T.; Taghizad, A.; Biannic, J.-M. Vision-based control for helicopter ship landing with handling qualities constraints. IFAC-PapersOnLine 2016, 49, 118–123. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, M.; Zheng, Z.; Low, K.H. Linear Velocity-Free Visual Servoing Control for Unmanned Helicopter Landing on a Ship with Visibility Constraint. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2979–2993. [Google Scholar] [CrossRef]
- Chen, Y.B.; Yu, J.Q.; Su, X.L.; Luo, G.C. Path Planning for Multi-UAV Formation. J. Intell. Robot. Syst. 2015, 77, 229–246. [Google Scholar] [CrossRef]
- Bassolillo, S.R.; Blasi, L.; D’Amato, E.; Mattei, M.; Notaro, I. Decentralized Triangular Guidance Algorithms for Formations of UAVs. Drones 2022, 6, 7. [Google Scholar] [CrossRef]
- Fei, Y.; Sun, Y.; Shi, P. Robust Hierarchical Formation Control of Unmanned Aerial Vehicles via Neural-Based Observers. Drones 2022, 6, 40. [Google Scholar] [CrossRef]
- Karimoddini, A.; Lin, H.; Chen, B.M.; Tong, H.L. Hybrid three-dimensional formation control for unmanned helicopter. Automatica 2013, 49, 424–433. [Google Scholar] [CrossRef]
- Hu, D.; Yang, R.; Zuo, J.; Zhang, Z.; Wang, Y. Application of Deep Reinforcement Learning in Maneuver Planning of Beyond-Visual-Range Air Combat. IEEE Access 2021, 9, 32282–32297. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver Decision of UAV in Short-Range Air Combat Based on Deep Reinforcement Learning. IEEE Access 2019, 8, 363–378. [Google Scholar] [CrossRef]
- Kivelevitch, E.; Ernest, N.; Schumacher, C.; Casbeer, D.; Cohen, K. Genetic Fuzzy Trees and their Application Towards Autonomous Training and Control of a Squadron of Unmanned Combat Aerial Vehicles. Unmanned Syst. 2015, 3, 185–204. [Google Scholar]
- Chamberlain, L.; Scherer, S.; Singh, S. Self-aware helicopters: Full-scale automated landing and obstacle avoidance in unmapped environments. In Proceedings of the 67th American Helicopter Society International Annual Forum 2011, Virginia Beach, WV, USA, 3–5 May 2011; pp. 3210–3219. [Google Scholar]
- Nikolajevic, K.; Belanger, N. A new method based on motion primitives to compute 3D path planning close to helicopters’ flight dynamics limits. In Proceedings of the 7th International Conference on Mechanical and Aerospace Engineering (ICMAE), Cambridge, UK, 18–20 July 2016; Volume 23, pp. 411–415. [Google Scholar]
- Schopferer, S.; Adolf, F.M. Rapid trajectory time reduction for unmanned rotorcraft navigating in unknown terrain. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Wyndham Grand, Orlando Resort, Orlando, FL, USA, 27–30 May 2014; pp. 305–316. [Google Scholar]
- Whalley, M.S.; Takahashi, M.D.; Fletcher, J.W.; Moralez, E.; Ott, L.C.R.; Olmstead, L.M.G.; Savage, J.C.; Goerzen, C.L.; Schulein, G.J.; Burns, H.N.; et al. Autonomous Black Hawk in Flight: Obstacle Field Navigation and Landing—Site Selection on the RASCAL JUH—60A. J. Field Robot. 2014, 31, 591–616. [Google Scholar] [CrossRef]
- Sridhar, B.; Cheng, V.H.L. Computer vision techniques for rotorcraft low-altitude flight. Control Syst. Mag. IEEE 1988, 8, 59–61. [Google Scholar] [CrossRef]
- Friesen, D.; Borst, C.; Pavel, M.D.; Stroosma, O.; Masarati, P.; Mulder, M. Design and Evaluation of a Constraint-Based Head-Up Display for Helicopter Obstacle Avoidance. J. Aerosp. Inf. Syst. 2021, 18, 80–101. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, B.; Meng, Z.; Zhou, Y. Integrated real time obstacle avoidance algorithm based on fuzzy logic and L1 control algorithm for unmanned helicopter. In Proceedings of the Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1865–1870. [Google Scholar]
- Chandrasekaran, R.; Payan, A.P.; Collins, K.B.; Mavris, D.N. Helicopter wire strike protection and prevention devices: Review, challenges, and recommendations. Aerosp. Sci. Technol. 2020, 98, 105665. [Google Scholar] [CrossRef]
- Merz, T.; Kendoul, F. Dependable Low-Altitude Obstacle Avoidance for Robotic Helicopters Operating in Rural Areas. J. Field Robot. 2013, 30, 439–471. [Google Scholar] [CrossRef]
- Wang, D.; Li, W.; Liu, X.; Li, N.; Zhang, C. UAV environmental perception and autonomous obstacle avoidance: A deep learning and depth camera combined solution. Comput. Electron. Agric. 2020, 175, 105523. [Google Scholar] [CrossRef]
- Aldao, E.; Gonzalez-Desantos, L.M.; Michinel, H.; Gonzalez-Jorge, H. UAV Obstacle Avoidance Algorithm to Navigate in Dynamic Building Environments. Drones 2022, 6, 16. [Google Scholar] [CrossRef]
- Hermand, E.; Nguyen, T.W.; Hosseinzadeh, M.; Garone, E. Constrained Control of UAVs in Geofencing Applications. In Proceedings of the 26th Mediterranean Conference on Control and Automation, Zadar, Croatia, 19 June 2018; pp. 217–222. [Google Scholar]
- Jiang, M.; Xu, C.; Ji, H. Path Planning for Aircrafts using Alternate TF/TA. In Proceedings of the Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3702–3707. [Google Scholar]
- Kosari, A.; Kassaei, S.I. TF/TA optimal Flight trajectory planning using a novel regenerative flattener mapping method. Sci. Iran. 2020, 27, 1324–1338. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.-x.; Nan, Y.; Yang, Y. A Two-Stage Method for UCAV TF/TA Path Planning Based on Approximate Dynamic Programming. Math. Probl. Eng. 2018, 2018, 1092092. [Google Scholar] [CrossRef]
- Hao, L.; Cui, J.; Wu, L.; Yang, C.; Yu, R. Research on threat modeling technology for helicopter in low altitude. In Proceedings of the 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016; pp. 774–778. [Google Scholar]
- Machovina, B.J. Susceptibility Modeling and Mission Flight Route Optimization in a Low Threat, Combat Environment. Doctoral Thesis, University of Denver, Denver, CO, USA, 2010. [Google Scholar]
- Woo, J.W.; Choi, Y.S.; An, J.Y.; Kim, C.J. An Approach to Air-To-Surface Mission Planner on 3D Environments for an Unmanned Combat Aerial Vehicle. Drones 2022, 6, 20. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, X.; Liu, X. TF/TA2 trajectory tracking using nonlinear predictive control approach. J. Syst. Eng. Electron. 2006, 17, 396–401. [Google Scholar] [CrossRef]
- Hilbert, K.B. A Mathematical Model of the UH-60 Helicopter; No. NASA Technical Memorandum 85890; NSNA: Washington, DC, USA, 1984. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar]
- Yang, L.; Liu, Z.; Wang, X.; Xu, Y. An Optimized Image-Based Visual Servo Control for Fixed-Wing Unmanned Aerial Vehicle Target Tracking with Fixed Camera. IEEE Access 2019, 7, 68455–68468. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Z.; Wang, X.; Yu, X.; Wang, G.; Shen, L. Image-Based Visual Servo Tracking Control of a Ground Moving Target for a Fixed-Wing Unmanned Aerial Vehicle. J. Intell. Robot. Syst. 2021, 102, 81. [Google Scholar] [CrossRef]
- Vanneste, S.; Bellekens, B.; Weyn, M. 3DVFH+: Real-Time Three-Dimensional Obstacle Avoidance Using an Octomap. In Proceedings of the Morse 2014—Model-Driven Robot Software Engineering, York, UK, 21 July 2014; Volume 1319, pp. 91–102. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Nie, L.; Li, D.; Tu, Z.; Xiang, J. An Autonomous Control Framework of Unmanned Helicopter Operations for Low-Altitude Flight in Mountainous Terrains. Drones 2022, 6, 150. https://doi.org/10.3390/drones6060150
Jin Z, Nie L, Li D, Tu Z, Xiang J. An Autonomous Control Framework of Unmanned Helicopter Operations for Low-Altitude Flight in Mountainous Terrains. Drones. 2022; 6(6):150. https://doi.org/10.3390/drones6060150
Chicago/Turabian StyleJin, Zibo, Lu Nie, Daochun Li, Zhan Tu, and Jinwu Xiang. 2022. "An Autonomous Control Framework of Unmanned Helicopter Operations for Low-Altitude Flight in Mountainous Terrains" Drones 6, no. 6: 150. https://doi.org/10.3390/drones6060150
APA StyleJin, Z., Nie, L., Li, D., Tu, Z., & Xiang, J. (2022). An Autonomous Control Framework of Unmanned Helicopter Operations for Low-Altitude Flight in Mountainous Terrains. Drones, 6(6), 150. https://doi.org/10.3390/drones6060150







