Multi-UAV Collaboration to Survey Tibetan Antelopes in Hoh Xil

Abstract

Reducing the total mission time is essential in wildlife surveys owing to the dynamic movement of animals throughout their migrating environment and potentially extreme changes in weather. This paper proposed a multi-UAV path planning method for counting various flora and fauna populations, which can fully use the UAVs’ limited flight time to cover large areas. Unlike the current complete coverage path planning methods, based on sweep and polygon, our work encoded the path planning problem as the satisfiability modulo theory using a one-hot encoding scheme. Each instance generated a set of feasible paths at each iteration and recovered the set of shortest paths after sufficient time. We also flexibly optimized the paths based on the number of UAVs, endurance and camera parameters. We implemented the planning algorithm with four UAVs to conduct multiple photographic aerial wildlife surveys in areas around Zonag Lake, the birthplace of Tibetan antelope. Over 6 square kilometers was surveyed in about 2 h. In contrast, previous human-piloted single-drone surveys of the same area required over 4 days to complete. A generic few-shot detector that can perform effective counting without training on the target object is utilized in this paper, which can achieve an accuracy of over 97%.

1. Introduction

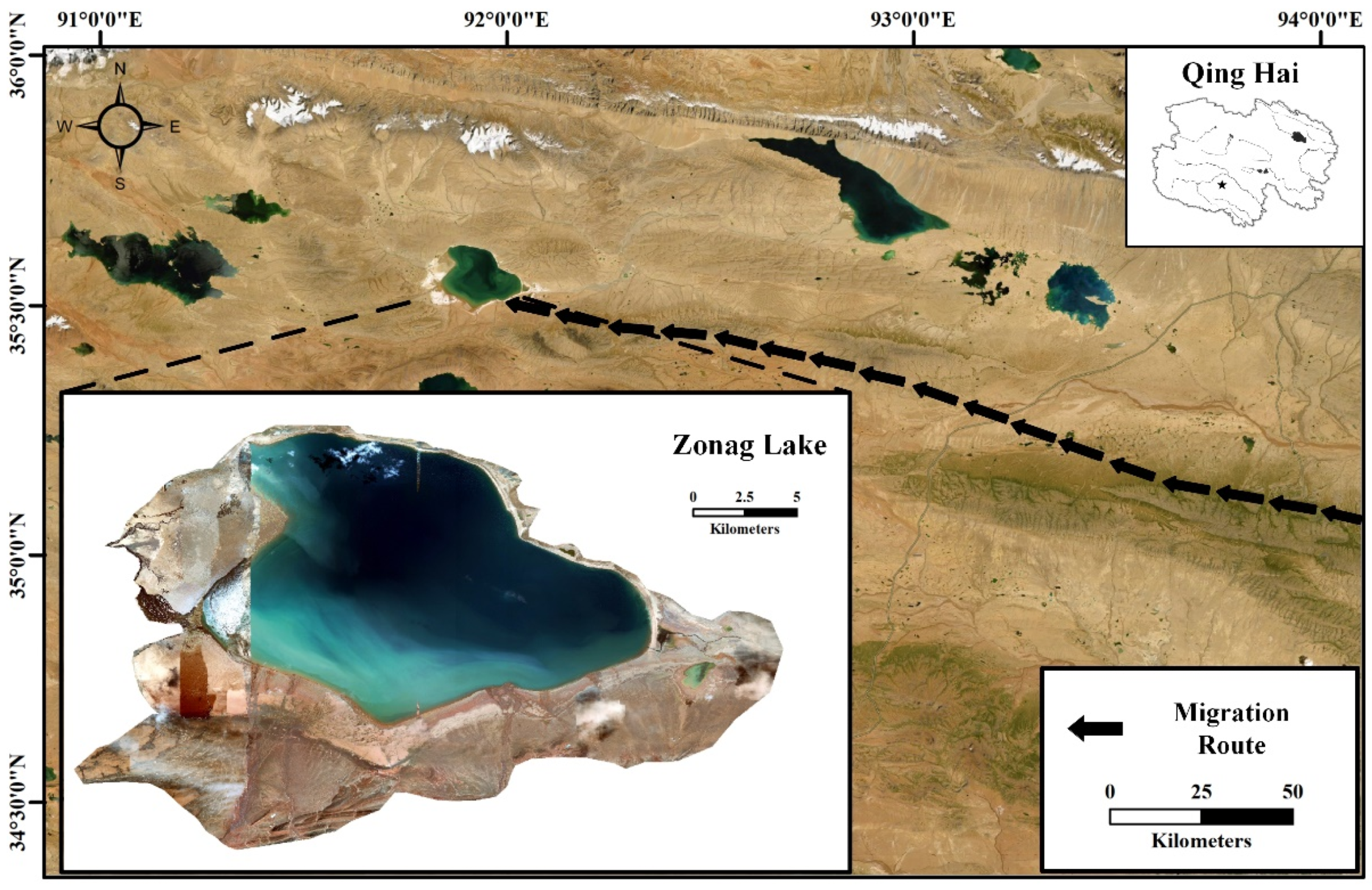
Located between the Tanggula Mountains and the Kunlun Mountains, Hoh Xil is one of the main water sources of the Yangtze River and the Yellow River [1]. It is a significant habitat for wildlife, such as Tibetan antelopes, black-necked cranes, lynxes, and wild yaks. Hoh Xil National Nature Reserve (HXNNR) was established in 1995. It was majorly divided into four national nature reserves, the Qiangtang, the Arjinshan, the Sanjiangyuan, and the Hoh Xil, located in Qinghai province. Furthermore, HXNNR joined the World Heritage List in 2017 for its unique biodiversity and environmental conditions [2], of which Tibetan antelopes constitute a highly representative population.

However, wild Tibetan antelopes have been listed as endangered by the International Union for Conservation of Nature (IUCN) [3]. Facing this heated issue, they are protected by the Wildlife Protection Law of China, and the Convention on International Trade in Endangered Species of Wild Fauna and Flora (CITES). Over the past century, hunting and grazing have been the main threats to the survival rate of the Tibetan antelope population. Worse, Tibetan antelopes’ poachers killed large numbers of antelopes for their hides and skins due to the enormous financial profits. From 1900 to 1998, the Tibetan antelope population declined from a million to less than 70,000, with a mortality rate of nearly 85%. In recent two decades, the Chinese government and wildlife conservation organizations have acted to constrain poaching, which has gained progress. Still, the deterioration of the antelopes’ natural habitat and environmental degradation continue to threaten their survival [4]. Owing to the shortage of funds and labor, reserve staff can only monitor limited areas but not the entire reserve. However, artificial ground investigation caused potential damage to the protection of fragile regions [5].

Traditional survey methods mainly include field surveys by vehicle or on foot. Nevertheless, Tibetan antelopes, especially females in pregnancy, are sensitive to the appearance of humans and vehicles, so surveys are usually conducted from a distance. This method can be appropriate during the non-migratory season when small groups are evenly distributed across the plateau. Still, it may lead to biased data where terrain features block sight lines, or animals are herded [6]. Moreover, some population surveys were conducted by land-based rovers remotely piloted within survey sites [7], but this method is not suitable for surveys in larger areas or uneven, rocky, and steeply sloping terrain. It is arduous to determine the population size with ground survey methods, as animal movements can cause violent fluctuations in density estimates. In addition, severe weather conditions in unpopulated areas often create much uncertainty at high altitudes, making it difficult for observers to access investigation areas [8]. Moreover, some zoologists tracked individuals through collars with global positioning system devices to identify calving grounds, migration corridors, and suitable habitats [1,9]. However, they cannot accurately and quickly estimate the number of animals or their distribution range, so new observation methods are needed.

In recent years, aerial surveys by UAVs in unpopulated areas, poor-developed transportation, and a fragile environment have become promising options [5,6]. Compared to full-size helicopters, small UAVs produce less noise flying at altitudes that can effectively obtain ground information and significantly reduce the disturbance to wildlife [10]. Fixed-wing UAVs have also been applied to wildlife surveys [11]. However, they are not suitable for the large-area survey missions in this survey, considering the take-off and landing environments and portability. Moreover, fixed-wing UAVs may also disturb wildlife as they may be perceived as avian predators [12]. In contrast, rotary-wing UAVs are more controllable and can obtain higher-resolution images, as UAVs can fly at lower speeds and altitudes without disturbing Tibetan antelopes [6]. Besides, using commercial rotary-wing UAVs can reduce the difficulty of flight operations for scientific investigations and allow researchers to focus on data analysis [13]. Moreover, UAV airports have been successfully applied in multiple fields recently [14], making regular unmanned aerial surveys possible. Utilizing multiple UAVs in an autonomous system can reduce manual requirements and conduct surveys with higher frequency and efficiency with the help of the short window period of weather, environments, and animal migration.

The efficiency of UAVs in conducting aerial surveys depends largely on the strategies the area coverage paths are planned. Generally, the complete coverage path-planning (CCPP) problem of a single UAV can be solved by sweep-style patterns, which guide the UAV back and forth over a rectangular space [15]. Other similar spatial sweep-style patterns include spiral patterns [16] and Hilbert curves [17]. Robotics designed to solve cyclic paths may encounter many tracebacks in sweep-style patterns [18]. Meanwhile, some tracebacks also occur in graphic search methods, such as wavefront methods [19,20]. Approaches that focus on minimizing the number of turns are often improved based on the minimum energy method [21,22], which is more suitable for fixed-wing or fast-moving aircraft. In contrast, we pay more attention to rotary-wing UAVs, consuming less energy during low-speed turns. In these path planning methods, the distance between the starting and ending points of the trajectories is often long. At the same time, unnecessary tracebacks may exist if the take-off and landing positions are far from the survey area. Moreover, it is time-consuming and inefficient for multiple sorties by a single UAV to perform coverage survey tasks in large areas. Presently, it is becoming a trend for multiple UAV formations to accomplish tasks jointly [23].

Most multi-UAV CCPP algorithms are extended based on the single-UAV area coverage research [24]. The common multi-UAV CCPP can be divided into two ways according to whether the task assignment is performed or not. In the multi-UAV CCPP without task assignment, each UAV may avoid collision with others by communicating with or regarding them as moving obstacles. After that, they complete area coverage tasks wholly and jointly. For instance, the path planning of each UAV is randomly generated by random coverage methods [25] and with a high traceback rate. There is also an improvement in the spanning tree coverage algorithm that employs multiple UAVs for complete coverage of a task area where there is acquired environmental information [26]. However, this method has poor robustness, and a planned trajectory’s quality depends on the robot’s initial position. In contrast, the research idea of the task assignment-based multi-UAV CCPP method is to divide a task area according to a certain way and assign the multiply divided sub-regions to each UAV. Then, each UAV plans its sub-region coverage trajectory within the region by a single UAV CCPP algorithm. For instance, task assignments of the sweep-style pattern [18] and polygonal area coverage [27] have been widely studied with high backtracking rates. Moreover, many of these methods are often used to find UAVs that satisfy appointed duration requirements. Moreover, many of these methods are often used to find UAVs that meet some endurance requirements. However, this paper mainly emphasizes generating optimal paths that satisfy a maximum path length constraint decided by UAV’s endurance conditions.

Therefore, we formulate the multi-robot CCPP problem according to the satisfiability modulo theory (SMT), which is a generalization of Boolean satisfiability because it allows us to encode all the specific survey-related constraints. Compared to the traditional traveling salesman problem (TSP), our method focuses more on finding feasible paths that satisfy a maximum path length constraint, allowing for vertex revisitation. Because the UAV’s battery constraints dictate the maximum path length, we can find solutions tailored to the limitations of the chosen UAV rather than finding a vehicle that would need to meet some endurance requirement. Although, our planning method is inherently a non-deterministic polynomial complete problem. The coverage problem can also be encoded as a MILP [28,29], it takes 4 to 6 days to solve problems for the same area, even using the most advanced solver on a powerful workstation. In contrast, the SMT method can generate available solutions in a few hours on a laptop [30].

The raw image shot by UAVs were assembled to form a large patchwork map. Then, this larger image is adopted for analysis. For example, ecologists leverage it to count flora and fauna for population analysis [31] or wildfire risk assessment in forests and grasslands [32]. However, most current counting methods can only be applied to specific types of objects, such as people [33], plants [34], and animals [31]. Meanwhile, they usually require images with tens of thousands or even millions of annotated object instances for training. Some works tackle the issue of expensive annotation cost by adopting a counting network trained on a source domain to any target domain using labels for only a few informative samples from the target domain [35]. However, even these approaches require many labeled data in the source domain. Moreover, obtaining this type of annotation is costly and arduous by annotating millions of objects on thousands of training images, especially when the photos of endangered animals are scarcer. The few-shot image classification task only requires learning about known or similar categories to classify images without training in a test, which is a promising solution [36,37]. Most existing works for few-shot object counting involve the dot annotation map with a Gaussian window of a fixed size, typically 15 × 15, generating a smoothed target density map for training the density estimation network. However, there are huge variations in the size of different target objects, and using a fixed-size Gaussian window will lead to significant errors in the density map. Therefore, to solve this problem, this paper uses Gaussian smoothing with adaptive window size to generate target density maps suitable for objects of different sizes. Once UAV aerial survey data have been collected and images have been analyzed to acquire accurate survey data, which can provide information on species distribution and population size, it also enables a deeper understanding of animals’ seasonal migrations and habitat changes. That is critical for preparing proper wildlife conservation policies and provides affluent data for ecologists. The focus of this paper is on the development of a multi-UAV system for conducting aerial population counting.

In this paper, we considered a path planning method with a set of aerial robots for population counting, which plans the trajectories of these robots for aerial photogrammetry. UAVs acquire a set of images covering the entire area with overhead cameras. It requires the images to have higher resolution and ensure enough overlap to stitch the images further together. Besides, aerial surveys should be conducted as soon as possible, owing to changing weather, light, and dynamic ground conditions. So it is necessary to require all UAVs to perform their tasks simultaneously. The collected UAV data and analyzed images will promote the sustainable development of population ecology. This paper focuses on developing a multi-UAV system for conducting aerial surveys to provide an autonomous multi-robot solution for UAV surveys and planning suitably for most survey areas.

This research is aimed at: (1) developing and testing a multi-UAVs CCPP algorithm for fast and repeatable unmanned aerial surveys on a large area that optimizes mission time and distance. Meanwhile, it compensates for the short battery life of small UAVs by minimizing tracebacks when investigating large areas. (2) Developing and testing a population counting method applicable to various species that does not require pre-training and large data sets.

The method in this paper is demonstrated in an extensive field survey of Tibetan antelope populations at the HXNNR, China. In this task, the celerity and repeatability of aerial surveys were conducted under extreme conditions on a large area. So, it can demonstrate the effectiveness of our system in facilitating the development of population ecology. In this paper, an investigating system of four UAVs observed a herd containing approximately 20,000 Tibetan antelopes distributed over an area of more than 6 km², which reduced the survey time from 4 to 6 days to about 2 h. The method put forward in this paper can complete aerial surveys in shorter distance and less mission time. For instance, this method reduced the total distance and mission time by 2.5% and 26.3%, respectively. Furthermore, the effectiveness increased by 5.3% compared to the sweep-style pattern over an area of the same size for the Tibetan antelope herd survey described in this paper.

2. Materials and Methods

2.1. Survey Area

Situated in southwest Qinghai Province, China (top right of Figure 1), the unpopulated areas of Hoh Xil are 83,000 square kilometers with an average altitude of 4800 m. The Zonag Lake and Sun Lake in northwest HXNNR (lower left of Figure 1) have been identified as the current principal calving grounds for Tibetan antelopes. The birth season reaches its peak from mid-June to July every year, when tens of thousands of female Tibetan antelopes from the TRHR (Three-Rivers Headwater Region), the Qiangtang Plateau of Tibet, and Hoh Xil migrate about 300 km southwest to the Zonag Lake and the Sun Lake for parturition [4]. Therefore, the Zonag Lake is also known as the “great delivery room of antelopes”. After calving, the antelope population will return to the northeast and arrive at the major overwintering pastures in mid-August.

Zonag Lake most frequently sees poachers. It is difficult to hunt antelopes because they usually are strong and vigorous. Most poachers decide to besiege Tibetan antelopes during the calving period around the Lake and kill them, which seriously affects the ecological balance of Tibetan antelope reproduction and leads to a sharp decline in population quantity. Tibetan antelopes are almost extinct.

One of the main calving grounds is presented in Figure 2. The water area of the Zonag Lake shrank drastically by 39% after the flood occurred in 2011. The western, southern, and eastern shorelines of the lake significantly altered, and the calving grounds of Tibetan antelopes on the southwestern shore also changed [2]. Recently, the government and organizations have gradually paid attention to conserving Tibetan antelopes. However, specific conservation efforts are often accompanied by the danger of entry into unpopulated areas, which requires high human costs and may cause unavoidable human interventions on the antelopes. In order to reduce costs in antelope population conservation and human interventions, we arranged a team of four rotary-wing UAVs to conduct aerial surveys and population counting in one of the main calving grounds of Tibetan antelopes located on the southwestern shore of the Zonag Lake. Meanwhile, we can learn more about the Tibetan antelope population’s reproduction and changes in calving grounds.

2.2. CCPP Methods

2.2.1. Path-Planning Problem Encoding

The multi-UAV CCPP problem was described as SMT in this paper, which is a popularization of SAT, as it allows us to encode all the specific survey-related constraints. SMT allows predicate logic in addition to the propositional logic used in the SAT solver.

$B_{i,a,t}\in \left\{0,1\right\}$ was set to be a Boolean variable where $i\in \left\{1,\dots ,N_{robots}\right\},a\in A=\left\{1,\dots ,N_{vertex}\right\},and t\in \left\{0,\dots ,T_{\max }\right\}$. The UAV $i$ is at the vertex $a\in A$ when the step is $t$ if $B_{i,a,t}=1$. The parameter $T_{\max }$ is the maximum trajectory allowed by any UAV. For instance, a UAV will pass through a maximum of 20 vertices if $T_{\max }=20$. For simplicity, it was assumed in this paper that all UAVs share the same $T_{\max }$ and there were enough UAVs to cover the entire map. The Figure $G\left(A,E\right)$ was constructed based on the survey areas, where there are various types of logical statements to describe the expected behaviors allowed by UAVs. The solver attempted to assign a value of 0 (False) or 1 (True) to each Boolean variable. By doing so, the values of these statements formed in the predicate logic are true. These logical statements can be considered constraints, like expression approaches to the optimization problem.

To strengthen the physical constraints of coverage, it is required to define that

$$\forall \left(i,t\right) \exists a B_{i,a,t}=1$$

(1)

works only for an $a$. This expression confines the UAV $i$ to the point $a$ at any given step $t$. Then, the UAV is only allowed to move to the vertex $y$ at the step $t+1$, given that it is in the vertex $a$ at the step $t$. Therefore, there is a line $\left(a~y\right)$ between these two vertices.

$$\neg B_{i,a,t}{\mathrm{A}}_{a~\mathrm{y}}{B}_{i,a,t+1}=1$$

(2)

Only the starting/ending vertex is connected to itself, and all other vertices have no self-loops. Next, it is defined that:

$$\forall a \exists \left(i,t\right)B_{i,a,t}=1$$

(3)

It enforces constraint requirements of the coverage task. For each vertex $a$ in the figure, there is at least a step $t$ where there is at least a UAV $i$ occupying the space. If there is only a pair of $\left(i,t\right)$ in a spot where the constrains must be satisfied, it will be equivalent to traveling salesman problem. The anti-collision constraint between UAVs may be achieved by, at most, one $i$ as required.

$$\forall a,t{ \mathrm{B}}_{i,a,t}=1$$

(4)

At the end, the starting and the ending points were coded in this paper by setting $a_i^0$ as the starting and ending vertices of the UAV $i$:

$$B_{i,a_i^0,0}=B_{i,a_i^0,T_{\max }}=1$$

(5)

It is expected that there is a closed-loop trajectory to ensure that UAVs do not have to return to the take-off location with repeated paths through the area. A separate boundary condition can be set if a closed-loop trajectory is not required, for the maximum trajectory length is determined by a UAV’s battery use. To find a feasible trajectory means that the UAV has enough power to arrive at the end of the trajectory. In an emergency recall, the UAV will have enough power to return, since the straight-line distance between any point of the trajectory and its ending point is at most the length of its remaining part. This feature allows the UAV to safely return to the starting point of the survey path when the vehicle cannot safely complete the survey (e.g., adverse weather conditions or poor visibility). It also encourages the UAV to end the survey at a spot near the starting point of the trajectory.

2.2.2. Model Optimization

• Variables reduction

The number of Boolean variables and the computing time can be reduced by leveraging the problem structure although these four constraints have fully encoded the multi-UAV coverage problem on SMT. It is assumed that each UAV can only move to an adjacent vertex at each time step, then the binary variables representing unreachable states can be removed from the problem to reduce the problem-solving time. Algorithm 1 describes the method.

2.

Sequential SMT

An SMT instance does not directly optimize the objective function but only finds a feasible solution at any time. The standard descending (or ascending) method was adopted in this paper to solve the objective function until the problem is infeasible to transform the feasibility framework into an optimization framework. Algorithm 1 performs this iterative process by repeatedly solving an SMT instance to identify the shortest trajectory. Each step is sequentially decremented by $T_{\max }$ according to a certain search dispatch until the user terminates the process or the problem is infeasible. Regarding problem structure, each subsequent iteration guarantees that the generated trajectory is no longer than that in the previous iteration if a solution is found. For instance, linear search dispatch for $T_{\max }$ is provided to Algorithm 1. However, in effect, any reasonable search dispatch is applicable.

3.

Parameter optimization

A parameter optimization algorithm (POA) [38] was adopted for the optimal trajectory. In this paper, the variational design of variables was performed by adding a normally distributed random value to each design variable, based on the evolutionary strategy of Schwefel’s [39] work. The goal of the POA is to minimize $f\left(x\right)$. We use $x_i$ to denote the candidate solution at the i-th generation. For each generation, we randomly mutate $x_i$ to obtain $x_i^{\prime }$. If $f\left(x_i^{\prime }\right)<f\left(x_i\right)$, then we set $x_{i+1}=x_i^{\prime }$.If $f\left(x_i^{\prime }\right)>f\left(x_i\right)$, then we use the following logic to determine $x_{i+1}$. If we had set $x_{k+1}=x_k^{\prime }$ at the previous generation k at which $f\left(x_k^{\prime }\right)>f\left(x_k\right)$, then we set $x_{i+1}=x_i^{\prime }$ with a 10% probability, and $x_{i+1}=x_i$ with a 90% probability. However, if we had set $x_{k+1}=x_k$ at the previous generation k at which $f\left(x_k^{\prime }\right)>f\left(x_k\right)$, then we set $x_{i+1}=x_i^{\prime }$ with a 50% probability, and we set $x_{i+1}=x_i$ with a 50% probability. This POA is greedy as it always accepts a beneficial mutation. However, it also includes some exploration in that it sometimes accepts a detrimental mutation. The probability of accepting a detrimental mutation varies, depending on whether or not the previous detrimental mutation was accepted. The algorithm for this POA is shown in Algorithm 1.

Algorithm 1 Model optimization algorithm

AcceptFlag indicates if the previous detrimental mutation replaced the candidate solution. The function of Distance() refers to time steps required to return to two vertices. In a linear grid, the function of Distance() refers to Manhattan distance required to return to two points.

2.2.3. Evaluation Indexes

The focus of this study is to reduce the total survey mission time and the total course flown by UAVs in order to accomplish a survey quickly while saving energy consumption. Therefore, the total course length was regarded as a constraint, rather than the result of a path planner’s calculation. The planning aims to satisfy the trajectory coverage requirement while minimizing the distance of tracebacks. The efficiency of a set of planned trajectories $R$ is defined as:

$${\eta }_{\mathrm{path}}=\frac{{\displaystyle \sum _i^R{S}_i}-{\displaystyle \sum _i^R{L}_i}}{{\displaystyle \sum _i^R{S}_i}}$$

(6)

$S_i$ is the total course length flown by the UAV $i$, $L_i$ is the sum of the UAV’s $i$ repeated flight paths and the distance from the take-off point to the survey area (also called transit distance). When the efficiency is 1, it means that the UAV took off within the survey area and had no repeated flight path.

2.3. Counting Methods

2.3.1. Adaptation and Matching Counting Network

In Figure 3, the network architecture of the animal counting algorithm adopted in this paper is depicted. Input to the network is the image $X\in {ℝ}^{H\times W\times 3}$ and several examples describing bounding boxes of the objects to be counted from the same image. Output from the network is the predicted density map $Z\in {ℝ}^{H\times W}$, and the counts of the interesting objects are obtained by summing up all density values. The network consists of two crucial modules: (1) a multi-scale feature extraction module; (2) a density prediction module. These two modules were designed in this paper for them to handle new categories in a test. ImageNet was adopted to extract features for such a network that can handle a wide range of visual categories. The feature extractor consists of a multi-layer convolution operation that maps the input into d-channel features. For the image $X$, it outputs a downsampled feature map $F\left(X\right)\in {ℝ}^{d\times h\times w}$. For an exemplar box $a$, the output feature map is further processed with global average pooling to form a feature vector $F\left(a\right)\in {ℝ}^d$.The density prediction module was designed to be incognizable to visual categories. The multi-scale feature extraction module consists of the first four blocks from a pre-trained ResNet-50 backbone [40]. Images were represented in this paper by convolutional feature mapping in the third and fourth blocks. In addition, ROI pooling was performed in this paper for the convolutional feature mapping from the third and fourth Resnet-50 blocks to obtain the examples’ multi-scale features.

The features obtained from the feature extraction module were not directly adopted in density prediction, in order to make the density prediction module incognizable to visual categories. Instead, the correlation mapping between sample features and image features was input to the density prediction module. The sample features were resized to different scales given the target objects at different scales should be considered. The resized sample features were associated with the image features to obtain multiple correlation maps, each of which corresponds to one scale. Scales of 0.9 and 1.1, as well as the original scales, were adopted in all experiments. The correlation maps were connected in series’ and fed to the density prediction module. The density prediction module consists of five convolutional blocks and three upsampling layers placed after the first, second, and third convolutional layers, respectively. The last layer is a 1 × 1 convolutional layer that predicts the two-dimensional density map. The size of the predicted density map is the same as the size of the input image.

2.3.2. Adaptative Window

The training images of a dataset were leveraged to train the network. Each training image contains multiple target objects. Moreover, most objects were only annotated with dots, while only the example objects were annotated with bounding boxes. However, it is difficult to train the density prediction network based on the training losses defined by dotted annotations. Most existing visual counting efforts, especially crowd counting [41], use a fixed size Gaussian window (usually 15 × 15) to convolve dotted annotated maps, thus generating smooth target density maps for training the density prediction network. The selected training dataset consists of 147 different categories in which the object size varies considerably [42]. Therefore, Gaussian smoothing with a self-adaptive window size was employed to generate the target density map. Firstly, the object size was estimated with dotted annotations. In a given dotted annotated map, each dot is nearly located at the center of the object. The horizontal distance $x_i$ and vertical distance $y_i$ between each dot $i$ and its nearest neighbor were calculated. With the modes $\stackrel{⌢}{x},\widehat{y}$ of $X$ and $X,Y\left(x_i\in X,y_i\in Y,i=1,2,3\dots n\right)$, the distance $d=\sqrt{{\left(\stackrel{⌢}{x}\right)}^2+{\left(\widehat{y}\right)}^2}$ can be calculated as the size of the Gaussian window to generate the target density map. The Gaussian standard deviation was set to be one quarter of the window size. The mean square error between the density prediction map and the ground truth density map was minimized to train the network. To match it, we adopted Adam optimizer with a learning rate of ${10}^{-5}$ and a batch size of 1. The height of each image was fixed at 384, and the width was accordingly adjusted to maintain the aspect ratio of the original image.

2.3.3. Loss Function

The above network structure only uses the samples’ example bounding boxes to extract their feature information. It does not fully use the position information provided by the exemplar boxes, while annotations by human eyes are crucial in this process. So we define the combination of two losses here to correct the model’s errors during the test.

• Count Loss

For each example bounding box, a, the sum of the density values within the box should be at least 1 because the exemplar box may also contain parts of other objects or overlap other objects with the same type to some extent. The following count loss was defined to quantify the number of constraint violations.

$${ℒ}_{count}={\displaystyle \sum _{a\in A}\max \left(0,1-{\Vert Z_a\Vert }_1\right)}$$

(7)

In this equation, A is the set of bounding boxes, and ${\Vert Z_a\Vert }_1$ the sum of all values in $Z_a$.

• Perturbation Loss

The density prediction map Z in essence is a correlation map between a sample and an image. Therefore, the density values near the sample should be similar to Gaussian distribution in an ideal circumstance. $G_{h\times w}$ was set to be a two-dimensional Gaussian window with the size of $h\times w$. The perturbation loss was defined as follows:

$${ℒ}_p={{\displaystyle \sum _{a\in A}\Vert Z_a-G_{h\times w}\Vert }}_2^2$$

(8)

• The Combined Adaptation Loss

The self-adaptation loss for testing is a weighted combination of the minimum count loss and the perturbation loss.

$${ℒ}_{Adapt}={\lambda }_1{ℒ}_{count}+{\lambda }_2{ℒ}_p$$

(9)

In the equation, ${\lambda }_1$ and ${\lambda }_2$ are coefficients of the count loss and the perturbation loss respectively. In testing, we referred to parameters setting [42], so as to perform 100 gradient descent steps for each test image and optimize the weighted loss of Equation (9). The learning rate adopted in this paper is ${10}^{-7}$. The values of ${\lambda }_1$ and ${\lambda }_2$ are, respectively, ${10}^{-9}$ and ${10}^{-4}$. The self-adaptation loss was only employed in testing. The loss function during training is the root mean square error between the density prediction map and the actual density map.

2.3.4. Evaluation indexes

The mean absolute error (MAE) and the root mean square error (RMSE) were adopted in this paper to measure the accuracy of counting methods, which are defined as follows.

$$\mathrm{MAE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|c_i-{\widehat{c}}_i\right|}$$

(10)

$$\mathrm{RMAE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(c_i-{\widehat{c}}_i\right)}^2}}$$

(11)

In these equations, $n$ refers to the quantity of test images, $c_i$ and ${\widehat{c}}_i$ are the ground truth and the predicted counts, respectively.

3. Results

3.1. Multi-UAVs CCPP

3.1.1. Summary of the Surveys

Considering the altitude of the animal survey area is around 5000 m, we chose a high-altitude low noise propeller. In this way, the UAVs can better adapt to the flight conditions at high altitudes and meet the noise limits of animal surveys. During the execution of the survey, the path spacing and flight altitude of the UAV are set according to the camera parameters and image stitching requirements. During non-mission execution (transit distance transit distance to and from the takeoff point and mission start point), the flight speed of the UAV is 10 m/s, which is determined by the environmental conditions and the specifications of the UAV. We want the speed to be as fast as possible under the premise of ensured safety and low noise. In addition, considering the safety withdrawal requirements and the actual hovering test results in abnormal weather, we set the safe flight time of the UAV at 28 min. Its detailed parameters are shown in

Table 1. Technical parameters of the aircraft.

Technical Parameters	Description	Technical Parameters	Description
Safe endurance time	28 min	Survey area flight speed	5 m/s
Maximum flight time	55 min	Transit distance flight speed	10 m/s
Maximum takeoff weight	9 kg	Maximum flight altitude	7000 m
Body weight with battery	6.3 kg	Flight height from ground	200 m
Autopilot	DJI flight control unit	Size (folded, including paddles)	430 × 420 × 430 mm (L × W × H)

.

During each survey, more than 6000 images were taken by a group of UAVs and stitched together to form a large, stitched image covering the entire survey area, as presented in Figure 4d. In this paper, these stitched images were employed to identify the number of Tibetan antelopes for estimating the population density of these groups. In our work, CCPP methods and population counting were emphasized rather than ecology.

Figure 4 shows the workflow of our system in the survey area (Figure 2). Firstly, we specified the interested area and divided it into grids with the spacing of 100 m between vertices, as shown in Figure 4a. Secondly, the CCPP algorithm is used to generate offline trajectories and optimize the starting and ending positions of the UAVs, as shown in Figure 4b. The four starting points are distributed in the vicinity of the survey area to ensure the optimal total flight distance and mission time for a group of UAVs. Thirdly, UAVs that execute these routes were activated to collect survey images at regular intervals. Figure 4c shows the image coverage area of each UAV. The images are stitched according to the UAVs’ time intervals and flight paths. The four different color blocks represent the captured areas by each of the four UAVs. Finally, these images were stitched together to generate a mosaic image, as shown in Figure 4d. The mosaic images will be used for animal counts to estimate population size, as described in Section 3.2.

12~13 flights (the flight number depends on the UAV position) were required to survey the area with four deployed UAVs in advance. It cost 2 days for a single manually piloted UAV to survey. However, in this paper, the survey can be completed in about 2 h in some regions of Zonag Lake by the proposed multi-UAV collaborative survey method. Using the autonomous system reduces the burden on manual requirements and realizes faster surveys with higher frequencies, thus enabling the exploitation of short windows in favor of the survey. That makes it more likely to make arrangements in advance and perform unmanned observation and data collection with the knowledge of animal migration routes.

The paths in Figure 4b were input to universal ground control software (UGCS) [43] for arranging the interface between a route planner and the UAV on-board flight computer. Although a trajectory is generated offline, its self-adaption allows a user to place the starting node at any position on it without recalculating the entire path. The entire course of each path is displayed in Figure 5. The UGCS will send a UAV command after it takes off so that the drone can execute the route and automatically land back at the starting point for recharging, thus preparing for the next flight.

3.1.2. Comparisons Ignoring Transit Distance

In this paper, we employed the SMT algorithm employed with the Z3 solver [44], the experimental calculations, which are performed under CPU:12th Gen Intel(R) Core(TM) i9-12900KF 3.20 GHz and the operating system of Windows11. Each computation takes about 15 s, and optimized calculation can get the best result in less than 100 epochs. We developed the algorithms on python and the commercial software ISIGHT, and we eventually ported them to python for ease of deployment and fast computation.

The proposed method in this paper was compared with both the common sweep-style method in the literature [18] and recently cell decomposition polygon coverage path planning method [27]. The sweep-style pattern was planned by using the area coverage function already realized in the UGCS [43]. The polygon coverage method divides the required region into polygons first, then plans coverage routes by using the sweep-style method, and last stitches these paths together with the TSP solver at the end. Moreover, Polygon division allows the solver to locally optimize the sweep direction of each polygon cell, which leads to shorter trajectories in most cases.

The efficiency of the polygon coverage method is higher than that of the simple sweep-style method, but there are still considerable tracebacks in both two methods because the core planning strategy of two methods lies are the sweep-style pattern. We compared routes of our trajectory planning algorithm, the standard sweep-style method, and the polygon division method in Figure 6. Although the sweep-style method has covered enough areas, it is influenced greatly by tracebacks, as presented in Figure 6b.

The path efficiency of our method, the sweep-style method, and the polygon method are demonstrated in

Table 2. Comparison of route efficiency. Bold entries indicate the most efficient set of routes.

Method	Parameters	Zone 1	Zone 2	Zone 3	Zone 4	Zone 5	Zone 6	Average
Ours	Length	5.9 km	4.7 km	4.4 km	3.6 km	2.5 km	1.5 km	-
	$N_{\mathrm{vertex}}$	132	109	102	82	62	56	-
	$N_{\mathrm{path}}$	136	112	104	85	65	61	-
	${\eta }_{\mathrm{path}}$	0.971	0.973	0.981	0.965	0.954	0.918	0.960
Sweep	Length	6.5 km	5.5 km	4.9 km	4.5 km	3.4 km	1.8 km	-
	Backtrack	0.57 km	0.98 km	0.37 km	0.63 km	0.52 km	0.08 km	-
	${\eta }_{\mathrm{path}}$	0.912	0.822	0.924	0.860	0.847	0.956	0.887
Polygon	Length	6.8 km	4.7 km	4.5 km	4.3 km	2.9 km	1.6 km	-
	Backtrack	0.80 km	0.51 km	0.38 km	0.61 km	0.33 km	0.17 km	-
	${\eta }_{\mathrm{path}}$	0.882	0.891	0.916	0.858	0.886	0.894	0.888

. The most effective set of paths is presented in bold. Algorithms in this paper realize the best efficiency in all but one case, with an average efficiency improvement of 8.2% compared to the sweep planner and 8.1% compared to the polygon coverage method. Without considering the transit distance of the planned trajectory, the sweep-style method results in a total course that is about 700 m longer than the trajectory generated by our method. The route generated by the polygon method is 400 m longer than that planned by our method. In all cases, the method proposed in this paper can reduce 366 m and 1.5 min compared to the polygon method, which will be 666 m and 2.2 min, compared to the sweep-style method.

3.1.3. Comparisons Considering Transit Distance

In an actual flight survey, there is a long distance between the UAV take-off point and the survey area. In the event of regular multi-UAV surveys, the take-off point may be flexibly arranged in advance before the survey window, which can reduce the impact of tracebacks and the consumption of UAV power to a certain extent. The total UAV flight distance was optimized in this paper within a given take-off area to make full use of the advantages of multiple UAVs.

We demonstrated the actual survey results of our method, the sweep-style method, and the polygon method in parts of the Zonag Lake (Figure 2) in

Table 3. Comparison of route parameters (distance, efficiency, and mission time). Set the total flight distance as the optimization parameter. Bold entries indicate the most efficient set of routes. The data are the average of 50 experiments.

Take-Off Plan	Method	Distance	Backtrack	${\mathit{\eta }}_{\mathbf{path}}$	Efficiency Improvement	Mission Time	Time Reduction
Two different take-off points within the area restrictions	Manual setting	94.2 km	20.8 km	0.779	Control group	2.6 h	Control group
	Sweep	94.1 km	20.8 km	0.779	0.00%	2.6 h	0%
	Polygon	94.0 km	20.7 km	0.780	0.13%	2.4 h	7.69%
	Ours	94.0 km	20.7 km	0.780	0.13%	2.4 h	7.69%
Four different take-off points within the area restrictions	Manual setting	94.2 km	20.8 km	0.779	Control group	2.6 h	Control group
	Sweep	91.8 km	18.4 km	0.799	0.00%	1.9 h	26.92%
	Polygon	91.6 km	18.3 km	0.800	0.13%	1.9 h	26.92%
	Ours	88.7 km	15.5 km	0.825	5.91%	1.7 h	34.62%
Four different take-off points without the area restrictions	Manual setting	95.8 km	22.4 km	0.766	Control group	2.6 h	Control group
	Sweep	92.4 km	16.2 km	0.795	3.79%	1.8 h	30.77%
	Polygon	89.0 km	15.6 km	0.825	7.70%	1.8 h	30.77%
	Ours	78.0 km	4.7 km	0.940	22.72%	1.7 h	34.62%

, where the effective set of trajectories are presented in bold. In Table 3, the take-off point is designated at the geometric center of the take-off area, based on empirical judgment. It is evident that the trajectory efficiency and the mission time are improved for different methods by flexibly configuring take-off points (number of starting points, restrictions on the starting area). Differences among the methods are few and finding the optimal set of paths is easy when there are two different take-off points. As the differences among algorithms grow when plans become more flexible, there are more starting points available for choosing. Moreover even the take-off area is no longer restricted to be outside the survey area (which is undesirable in animal surveys because the noise from the UAV may be perceived as a threat). The method proposed in this paper demonstrates the best path’s efficiency and the shortest time consumption under all three different plans, with a 22.72% increase in trajectory efficiency and a 34.62% reduction in mission time with unrestricted starting area. The method may reduce at most 54 min of the mission time, when compared to the manual setting method (designate starting points according to experience), which is equivalent to the time about twice as long as the maximum UAV endurance time.

During short-term and quick surveys, the flight time of UAVs is a factor to be fully considered to make full use of the valuable survey window. Shorter aerial survey time can help accomplish more surveys and capture more data throughout the breeding season. Based on the above methods, the total UAV flight distance and total mission time were optimized in this paper within a given planned take-off area.

Table 4. Comparison of route parameters (distance, efficiency, and mission time). Set the weighted sum of total flight path and total mission time as optimization parameters. Bold entries indicate the most efficient set of routes. The data are the average of 50 experiments.

Take-Off Plan	Method	Distance	Backtrack	${\mathit{\eta }}_{\mathbf{path}}$	Efficiency Improvement	Mission Time	Time Reduction
Two different take-off points within the area restrictions	Manual setting	94.2 km	21.6 km	0.771	Control group	2.6 h	Control group
	Sweep	95.0 km	21.7 km	0.772	0.13%	2.5 h	3.85%
	Polygon	95.0 km	21.3 km	0.776	0.65%	2.3 h	11.54%
	Ours	94.4 km	20.8 km	0.780	1.17%	2.2 h	15.38%
Four different take-off points within the area restrictions	Manual setting	94.2 km	20.8 km	0.779	Control group	2.6 h	Control group
	Sweep	91.8 km	18.5 km	0.799	0.00%	1.9 h	26.92%
	Polygon	92.7 km	19.0 km	0.795	2.05%	1.7 h	34.62%
	Ours	89.5 km	16.1 km	0.820	5.26%	1.4 h	46.15%
Four different take-off points without the area restrictions	Manual setting	95.8 km	22.4 km	0.766	Control group	2.5 h	Control group
	Sweep	90.8 km	21.2 km	0.866	11.55%	1.5 h	42.31%
	Polygon	80.3 km	7.0 km	0.913	19.19%	1.4 h	46.15%
	Ours	77.4 km	4.1 km	0.947	23.63%	1.2 h	53.85%

shows the actual test results of our method and other methods in some parts of Zonag Lake. If the configuration of starting points is more flexible (number of starting points, restrictions on the starting area), the metrics of the different methods will improve accordingly. This is similar to the results of the method mentioned above, that optimizes only the total flight distance of a group of aircrafts. The variation between algorithms is increasing as plans become more flexible, starting points become more selective, and even take-off areas are no longer restricted to survey areas. Our method shows the best trajectory efficiency and the shortest task time among all three different schedules, with a 23.63% improvement in path efficiency and a 47.83% reduction in task time as the starting area is unrestricted. Our method’s flight distance is unchanged, compared to methods only optimizing the total flight distance while the total mission time decreases from 2.6 h to 1.2 h at most, with an improvement of 19.23%. The method proposed in this paper witnesses an average improvement of 12.82% with three different take-off plans. Meanwhile, it can reduce mission times by up to 66 min, compared to manual setup methods, which are about twice the safe endurance time.

3.2. Population Counting

3.2.1. Comparison with Few-Shot Approaches

The performance of counting effects of our method was compared with that of other methods. There are two common baselines, namely (1) always outputting the average object quantity of the training images; (2) always outputting the mid-value counts of the training images. The two popular algorithms are: feature reweighting (FR) few-shot detectors [36] and few-shot object detection (FSOD) [37]. The method adopted in this paper is more advance than others, as presented in

Table 5. Comparing our method to two simple baselines (mean, median) and two popular algorithms (FR few-shot detector, FSOD few-shot detector). These are few-shot methods that have been adapted and trained for population counting. Our method has the lowest MAE and RMSE on Tibetan antelope dataset. Bold entries indicate the most efficient method.

Method	MAE	RMSE
Mean	48.7	146.7
Median	47.7	152.4
FR few-shot detector	41.7	141.0
FSOD few-shot detector	35.5	140.7
Ours	23.2	98.4

.

3.2.2. Comparison with the Object Detector

One of the other counting methods is to use detectors to count objects after they have been detected, which is only applicable to certain categories of objects with pre-trained detectors. In general, training object detectors requires thousands of examples, so it is not a practical approach for general visual counting. The performance of the network on a validation set with pre-trained object detectors and on categorized subsets of a test set was evaluated in this paper. To be specific, we compared our method with Faster R-CNN [45] and Mask R-CNN [46]. These two pre-trained detectors can be found in the Detectron2 library [47]. The comparison results are shown in

Table 6. Comparing our method with pre-trained object detectors. Bold entries indicate the most efficient method.

Method	MAE	RMSE
Faster R-CNN	36.5	79.2
Mask R-CNN	35.2	79.8
Ours	23.9	45.4

. It can be seen that our method outperforms target detectors that have been pre-trained with thousands of annotated examples.

3.2.3. Qualitative Analysis

Figure 7, Figure 8, Figure 9 and Figure 10 shows the visual prediction results of our algorithm. The input was the image to be tested and several bounding boxes of counting objects. In order to analyze the correctness of the density map expediently, we showed the input image and the density map superimposed. Figure 7 and Figure 8 show examples of Tibetan antelope images with different densities from the aerial view of the UAVs, which has proved the algorithm works well in the case of a flat background from an overhead view with more than 97% correct counting rate. Furthermore, the model still has an accuracy rate of more than 97% in the case of complex backgrounds (Figure 9), where both water and land are present in the overhead view and the color of the land is close to that of Tibetan antelope. Figure 10 shows an example of a Tibetan antelope herd image taken from the side view of a UAV flight, which has a correct counting rate of over 96%. The overhead and side view results demonstrate the robustness of the method utilized in this paper for counting Tibetan antelopes photographed from different viewpoints.

4. Discussion

The study demonstrates that daily monitoring in protected areas is greatly complemented by surveys of wildlife, which are conducted by small, low-cost, multiple rotary-wing UAVs in large areas. However, the influence of UAVs’ noise and appearance on wildlife should be considered during surveys. As we only surveyed and analyzed Tibetan antelopes, prior detailed testing on the UAV’s influence of noise and movements should be conducted when this method is applied to other animals. Moreover, our method extends the field of UAV application and provides an autonomous multi-robot solution for UAV path planning, which is suitable for any size of the survey area. It can also select the appropriate path according to the existing UAV parameters and allows them to optimize the take-off point of each flight.

The flexible deployment of multiple UAVs can significantly improve the path efficiency for completing area coverage missions and reducing manual survey time and manpower consumption, especially in remote and unpopulated areas. The results of multi-UAV trajectory planning (Table 2 and Table 3) have been visualized in Figure 11, Figure 12 and Figure 13. Regarding the total distance and the mission time, our method has more edges over the current multi-UAV CCPP methods. In one aspect, the shorter total distance means less energy consumption, which indicates a group of recharged UAVs can complete more flights when deployed at a UAV airport. In another aspect, a shorter mission time means that a quicker survey, allowing more surveys to be done within a window period to reduce da-ta errors and learn about timing-related issues. It can provide ecologists with more options for their survey methods. Compared to the method where only the total distance is done, both the total distance and mission time decline when these two indicators are optimized simultaneously. This is because the planner divides and distributes the entire survey route task to each with different take-off points evenly while acquiring the optimal solution for the area to survey on its own.

The few-shot object counting method can be used without pre-training the model via images of the target population. This improves the universality of the counting method to a certain extent, and it can be applied to many different fields. When using this method to test the photos of Tibetan antelope taken by UAVs, it has good applicability to images of different densities and perspectives. It can meet the requirements of population counting. A particular animal can be repeatedly photographed when images are stitched together because of the possible animal movements during a multi-UAV survey. Ecologists focusing on data research need to correct the survey results to ensure the accuracy of data results, which has become a necessary research subject [48]. Therefore, it is essential to reduce the mission time of such investigations. The information obtained directly from traditional ground surveys is often one-dimensional. The distribution of all animals may be visually linear (Figure 14) if interpreted from an image perspective when surface observation is conducted on the ground [49]. These factors often lead to significant errors in the results, which is not conducive to animal counting. When compared with traditional field survey methods by vehicle or on foot, UAV surveys have a better field of view (Figure 7, Figure 8 and Figure 9) and have reduced the impact of animal movements on the data to a large extent, which can improve the survey accuracy.

With the current development of commercial multi-rotary-wing UAVs and UAV airports, an untrained layman may acquire the skills to control a rotary-wing UAV quickly. The aerial animal counting system with multi-UAVs, developed by us, aims to enable scientists to focus on experimental design and data analysis rather than flight control skills. The survey deployment can be made before the survey window through a simple setup that determines the surveyed areas, the take-off areas, and the UAVs’ information. The current artificial intelligence methods can quickly assist humans in completing many of tedious counting tasks. The approach proposed in this paper can replace humans in performing uninterrupted unmanned count surveys, and we only need to ensure that UAVs will not influence the ecology of the survey areas.

However, more sorties of UAVs are often required for conducting simultaneous surveys of large areas, due to UAV endurance limitations. Besides, excessively high-flight altitudes, which means reducing the impact of UAV noise on animals, may not be conducive to animal counting in feature identification. It does harm to the applicability of the multi-UAV survey method because of camera resolution. UAV aerial surveys will also integrate more features by combining visible light and multispectral and thermal infrared cameras to improve information accuracy further.

5. Conclusions

A general and flexible CCPP method was provided in this paper for a group of UAVs to count animals. This planning algorithm enables scientists to employ multiple drones to conduct regular unmanned surveys in the uninhabited region in fragile environments with poor access. Moreover, multiple UAVs allow faster surveys with higher frequencies, lower costs, and greater resolution than helicopters and better leverage for rare observation opportunities by reducing wildlife disturbance from human activities. We have implemented our algorithms on a set of UAVs and conducted field experiments. The rapid and repeatable aerial surveys of large-scale environments demonstrated the utility of our system in facilitating population ecology. The results unveil that, in this paper, a herd containing approximately 20,000 Tibetan antelopes distributed over an area of more than 6 km² was observed by a measuring system of four UAVs, which reduced the survey time from 4 to 6 days to about 2 h. Our method can complete aerial surveys in shorter trajectories and mission time. With this method, the trajectories and time were reduced by 2.5% and 26.3%, respectively, and the effectiveness increased by 5.3% when compared to sweep-style paths over an area of the same size.

Different from the target detector methods commonly used in current counting methods, the current work mainly focuses on one specific category at a time, such as people, cars, and plants. In this paper, we use a general few-shot adaptive matching counting method, which can count effectively without pre-training through the objects to be measured. We tested the photos of Tibetan antelope taken from the UAV, and the accuracy can reach more than 97%. The survey data will facilitate the development of animal protection policies. The results of the later survey can contribute to the development of animal protection policy, which is conducive to protecting and promoting ecological sustainability. However, animals may move in the process of multi-drone surveys, which makes photos of them possible to be duplicated when stitched together. In the future, reasonable corrections based on the survey results can further improve the accuracy of the survey. Other investigations that require fast aerial surveys under unpopulated circumstances can also benefit from our algorithms, such as surveys of other wildlife populations, forests, and shrublands.