CARLA+: An Evolution of the CARLA Simulator for Complex Environment Using a Probabilistic Graphical Model

Abstract

In an urban and uncontrolled environment, the presence of mixed traffic of autonomous vehicles, classical vehicles, vulnerable road users, e.g., pedestrians, and unprecedented dynamic events makes it challenging for the classical autonomous vehicle to navigate the traffic safely. Therefore, the realization of collaborative autonomous driving has the potential to improve road safety and traffic efficiency. However, an obvious challenge in this regard is how to define, model, and simulate the environment that captures the dynamics of a complex and urban environment. Therefore, in this research, we first define the dynamics of the envisioned environment, where we capture the dynamics relevant to the complex urban environment, specifically, highlighting the challenges that are unaddressed and are within the scope of collaborative autonomous driving. To this end, we model the dynamic urban environment leveraging a probabilistic graphical model (PGM). To develop the proposed solution, a realistic simulation environment is required. There are a number of simulators—CARLA (Car Learning to Act), one of the prominent ones, provides rich features and environment; however, it still fails on a few fronts, for example, it cannot fully capture the complexity of an urban environment. Moreover, the classical CARLA mainly relies on manual code and multiple conditional statements, and it provides no pre-defined way to do things automatically based on the dynamic simulation environment. Hence, there is an urgent need to extend the off-the-shelf CARLA with more sophisticated settings that can model the required dynamics. In this regard, we comprehensively design, develop, and implement an extension of a classical CARLA referred to as CARLA+ for the complex environment by integrating the PGM framework. It provides a unified framework to automate the behavior of different actors leveraging PGMs. Instead of manually catering to each condition, CARLA+ enables the user to automate the modeling of different dynamics of the environment. Therefore, to validate the proposed CARLA+, experiments with different settings are designed and conducted. The experimental results demonstrate that CARLA+ is flexible enough to allow users to model various scenarios, ranging from simple controlled models to complex models learned directly from real-world data. In the future, we plan to extend CARLA+ by allowing for more configurable parameters and more flexibility on the type of probabilistic networks and models one can choose. The open-source code of CARLA+ is made publicly available for researchers.

1. Introduction

The advancement in sensor technologies, mobile network technologies, and artificial intelligence has pushed the boundaries of different verticals, e.g., healthcare, autonomous driving, etc. Statistics show that more than one million people are killed in traffic accidents yearly, and the vast majority of the accidents are caused by human negligence [1]. Therefore, the realization of safe and robust autonomous driving (AD) has the potential to drastically reduce road traffic accidents, congestion, and excessive fuel consumption by shifting the driving control from humans to autonomous vehicles.

The Society of Automotive Engineers (SAE) [2] classifies autonomous vehicles into six levels of autonomy. Most of the autonomous driving features that are currently commercially available in Level (L) 2 and L3 autonomous vehicles (AVs) are Advanced Driving Assistance Systems (ADAS) and were first deployed in structured and controlled environments such as highway driving and low-speed parking. However, in urban and uncontrolled environments, the presence of mixed traffic of autonomous vehicles, classical vehicles, vulnerable road users, e.g., pedestrians, cyclists, and dynamic unprecedented events make it challenging for the classical AV to safely navigate the traffic, reduce travel delay, and avoid congestion. Therefore, the classical autonomous driving of L2 and L3 are pushing toward the L5 fully autonomous driving. In relation to this, both industry and research communities have been working on and contributing solutions such as collaborative autonomous driving to realize a higher level of autonomous driving.

Collaborative autonomous driving solutions have been around for some time. However, the focus has been on lower automation levels and vehicular networks. Behavioral planning, local planning, and inter-vehicular communication for lower automation levels are simpler when compared with the envisioned higher automation levels that involve different weather dynamics, congested settings, many lanes populated with vehicles of varying speeds, roundabouts, crossings, pedestrians, etc. These complex dynamics ask for the collaboration of short-time quanta and a varying number of collaborating vehicles. The solution to these challenges necessitates a newer design goal of the evolved version of collaborative autonomous driving. However, an obvious challenge in this regard is how to create a dynamic and uncertain environment that realistically captures the complex dynamics of this problem domain. Thus, to create and validate the solutions to these and similar problems, a realistic environment is required for which the researchers heavily rely on different options such as (i) simulators, (ii) emulators, and (iii) real environment. Testing autonomous vehicles in real-time on public roads has always been extremely challenging due to the high cost of the required infrastructure, high-performance computing, sensors, and communication equipment, jeopardizing public safety. This is where simulation testing helps to fill the research gap and democratize autonomous driving research.

In this research, we opt for simulation-based testing to define, model, and simulate the dynamic and uncertain environment that realistically captures the dynamics of a complex and urban environment. There are a bunch of simulators that are being used by researchers in this area such as RRADS [3], TORCS, and Udacity [4]. However, these simulators lack the environmental dynamics and complexity, such as predicting and controlling the behavior of pedestrians, road junctions, traffic laws, and other complex dynamics, that differentiate urban driving from simple track racing. In addition, some closed-source commercial simulators such as Grand Theft Auto V and ANSYS offer little environment customization and control, restricted kinematic behavior, limited scripting, and use case scenario descriptions, constrained sensor suite specification, and various other limitations caused by the commercial nature of the simulator. CARLA (Car Learning to Act) being one of the prominent simulators, provides rich features and environment, however, it still fails on a few fronts such as not being able to fully capture the complexity of the urban environment. Moreover, it mainly relies on manual code, and multiple conditional statements, and provides no pre-defined way to do things automatically based on the dynamic simulation environment. Therefore, there is a dire need to extend the off-the-shelf CARLA simulator with more sophisticated settings that can capture the required dynamics and address the challenges of a higher level of autonomous driving.

The novelty of this research lies in contributing to introducing the complex dynamic environment through probabilistic graphical models (PGM) in the classical CARLA. The motivation for using PGM is that it is a robust framework for encoding probability distributions for this complex domain by computing the joint distributions over numerous random variables that interact with one another. Furthermore, the experimental environment is carefully designed, developed, and implemented by capturing the relevant dynamics of specialized use cases of complex and urban driving.

Some of the main contributions of this research are:

• Modeling the complex urban environment based on a state-of-art probabilistic graphical model which is suitable for capturing the dynamics specific to urban and higher-level autonomous driving;
• Design and development of an extension of CARLA referred to as CARLA+ by integrating the PGM framework. Instead of manually catering to each condition, it provides a unified framework to automate the behavior of dynamic environments leveraging PGMs;
• Experimentation and validation of the proposed CARLA+ extension.

The paper is structured into six sections. Section 2 provides the background information to comprehend the contents of this paper. Section 3 presents an overview of state-of-the-art simulators and relevant studies. Section 4 elaborates on the design and development of the proposed CARLA+ extension. Section 5 discusses the experimental setup and different settings of experiments to validate the CARLA+ solution. Finally, Section 6 elucidates the conclusion of the study.

2. Background

This section aims to equip the reader with some background information to comprehend the contents of this paper.

2.1. Autonomous Driving Design Goals

The ability to sense their surroundings using a variety of sensors allows autonomous vehicles to operate without any human intervention. Perception, planning, and control are the essential components of autonomous vehicle development. Each layer is responsible for layer-specific operations and decisions. Therefore, realizing the interactions between layers for various use case scenarios helps in achieving a higher level of autonomy. The Society of Automotive Engineers (SAE) establishes design objectives and classifies vehicles into six categories based on their degree of automation. Levels 0 to 2 can widely be defined as driver-assisted, Levels 3 and 4 as semi-automatic, and Level 5 as fully autonomous. The progression from Level 1 to Level 5 requires the development of numerous additional features in autonomous vehicles. It is believed that Level 5 autonomous vehicles will be able to drive and execute maneuvers optimally in a complicated urban environment, handling unprecedented events, and assuring traffic efficiency, and road safety. Therefore, a collaborative autonomous driving paradigm shift is necessary for classical autonomous driving to realize a higher level of autonomy. In an uncontrolled and mixed traffic environment, the solutions of Level 2–3 AVs relying solely on the onboard perception of the environment, and limited visibility are impractical for classical autonomous vehicles to navigate and take decisions. Therefore, the complex dynamics of these environments ask for new short-time collaboration solutions with a varying number of collaborating vehicles.

For ready reference, in what follows next, we briefly discuss the features of SAE levels and their testing requirements in simulation in

Table 1. Testing and Simulation Requirements to meet SAE Automation Levels.

SAE Level of Automation			Testing Requirements
Level (L)	Description	Example
L0	No Automation: There should always be a human driver in the vehicle performing the dynamic driving task. Only warnings and temporary assistance are offered as features.	Blind spot warning	Simulation of traffic flow, multiple road types, radar and camera sensors
L1	Driver Assistance: It is necessary to have a driver at all times. Steering or brake/acceleration control is provided through features.	Adaptive Cruise Control (ACC) & Lane centering	All of the above (AoB) in addition to simulation of vehicle dynamics and ultrasonic sensors
L2	Partial Driving Automation: the system is in charge of longitudinal and lateral vehicle motion within a constrained operational design domain. Features include both steering and brake/acceleration control.	ACC & lane centering at the same time.	AoB and the simulation of a driver monitoring system and machine–human interaction
L3	Conditional Automation: in case of any failure, the system can request the human intervention.	Traffic Jam Chauffer	AoB and the simulation of traffic infrastructure and dynamic objects
L4	High Automation: the automated driving system is in charge of detecting, observing, and reacting to events. Features can operate the vehicle in a few limited scenarios.	High Driving Automation	AoB and simulations of various weather conditions, lidar, camera, and radar sensors, mapping, and localization
L5	Full Automation: L5 AVs will be able to navigate through complicated environments and deal with unforeseen circumstances without human interaction.	Robo-Taxi	All of the above, along with adhering to all traffic laws, norms, and V2X communication

.

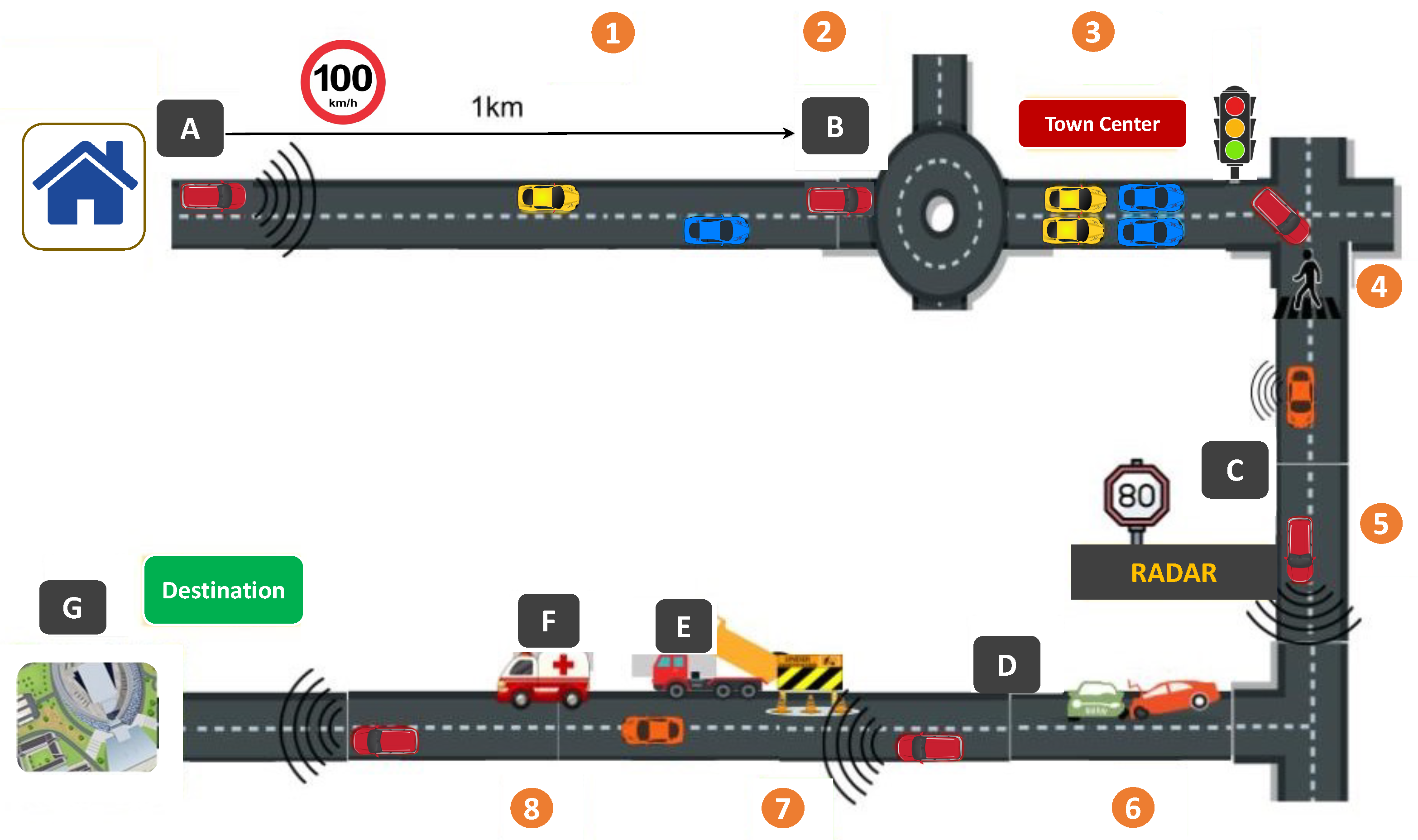
2.2. Complex Dynamics of Urban Environment

The race to fully L5 autonomous vehicles is still going on, and the stakeholders, including automakers and technology pioneers, are continually refining their approaches to reaching the necessary level of automation for their vehicles. The testing grounds play a crucial role in assessing the capability of autonomous vehicles under various environmental dynamics. A key goal of testing grounds is to provide a realistic setting that accurately simulates the environment in which autonomous vehicles will operate in the real world. However, one of the challenging questions is whether autonomous vehicles be able to handle unexpected and sophisticated scenarios.

The complex urban environment is a buzzword, and there is no one common concrete definition of it, even though the 3rd Generation Partnership Project (3GPP) [5] standardization body and different stakeholders have contributed with different use cases which we have already studied in our research literature surveys [6,7]. Based on our extensive research on understanding the complex urban environment, we provide our definition of a complex environment and have created a high-level abstract Figure 1, which captures the most relevant dynamics which are representative of a complex urban environment.

For an easy understanding of the complex urban environment and to highlight the challenges of specific urban environment settings, we decompose the environment into various scenes as shown in Figure 1. These scenes include: (i) Scene 1 with Lesser Dynamics—as it can be seen, that scene 1 between $A\to B$ focuses on the road segment that presents straightforward dynamics, e.g., clearly marked roads, smooth traffic, etc. Such dynamics ask for simplistic environmental understanding and consequently a limited set of critical maneuvers. Furthermore, in this scene, the local perception of the environment is good enough for AV to make decisions. (ii) Scene 2 with Roundabout Challenge—in this scene, the autonomous vehicle is faced with going through a roundabout, which is a challenging scenario that requires consistent interaction with other vehicles. In this scene, it is not possible for an AV to cross the roundabout and interact with the neighboring vehicles solely relying on its onboard sensors. Therefore, it is indispensable for the AV to have an extended perception of the environment by collaborating with the neighboring vehicles leveraging vehicle-to-vehicle (V2V) communication, and creating short-term platoons. The collaboration would result in increased safety and traffic flow at the roundabout. (iii) Scene 3 with Congestion Settings—the road segments that are usually in the city centers with a lot of traffic and reduced speed. In this scenario, the local perception of the environment is not enough for the AV to navigate safely and timely in these congested settings. Therefore, realizing the solution of autonomous driving for such settings requires enhanced vehicular collaboration and platooning format for very short time quanta. (iv) Scene 4 with Sharp Turn and Vulnerable Road Users—the challenge is obvious for vehicles that solely rely on onboard sensors. These classical vehicles would not be able to detect pedestrians due to manifold reasons: (1) due to the limited local perception of the vehicle; (2) occlusion and deformation; (3) due to weather conditions. It is claimed that the realization of the collaboration using V2V and vehicle-to-infrastructure (V2I) communication would provide AVs with an extended perception of the environment as a result, accurately predicting the pedestrians and vulnerable road users. (v) Scene 5 with Sudden Speed Change Zones—the road segments with a sudden change in the speed zones force the vehicles to react unprecedentedly. The AV equipped with heterogeneous sensors (camera, LiDAR, Radar, etc.) is capable of detecting road signs, however, the conventional decision making with a narrow environmental understanding and short lifespan of decisions in terms of time and distance would compel the AVs to make myopic decisions, resulting in erroneous decisions, injuries, fatalities, etc. Hence, having such information known in advance leveraging collaboration with far-ahead vehicles would allow the vehicles to react proactively in a timely and safe manner. (vi) Scenes 6 and 7 with meeting road blockage due to accident—such situations are unprecedented and hamper the usual traffic flow. In these scenarios, relying solely on the local perception of the environment would not allow the AV to know about the accident in advance, resultantly omitting the vehicle to take decisions in advance. Therefore, it asks for dynamic adaptation of the collaboration with other road users including other vehicles. Furthermore, the need for extended collaboration may prove to be instrumental (i.e., by implementing the collaboration with farther vehicles/groups of vehicles, etc.) Collaboration with farther vehicles would allow the AV to have a wider perception of the environment in advance and take optimal decisions proactively. (vii) Scene 8 with an emergency vehicle on the road—in situations, where emergency vehicles appear on the road, the norm of usual traffic is to be avoided. Such situations could also be handled by efficient collaboration among the vehicles. Collaboration would enable the AVs to communicate directly with each other or through the smart tower deployed on the road and make way for the emergency vehicle.

We believe that the aforediscussed scenes to a greater extent capture the dynamics of the complex urban environment. It should be highlighted that the problem of modeling and implementing a collaborative autonomous driving solution will take into account these and similar challenges of the urban complex environment.

3. Related Work

The related work is divided into two sub-sections. Section 3.1 scrutinizes the state-of-the-art simulators and their comparison however, Section 3.2 discusses the studies pertinent to the proposed work.

3.1. Autonomous Driving Simulators—An Overview

Considering the complexity of a dynamic urban environment, the system must be evaluated in a wide range of settings and situations to validate the entire autonomous driving architecture which would enormously increase the cost and development time using the physical method. Given this, leveraging virtual development and validation testing and designing acceptable driving scenarios are currently the cornerstones to building reliable and safe autonomous vehicles. These simulators have developed over time, moving beyond simply simulating vehicle dynamics to simulating more intricate functionalities. Therefore, autonomous vehicle technology testing simulators must meet specifications that go beyond, simulating actual vehicle models to include several sensor models, decision-making, path planning, control, and more.

In what follows next, we briefly discuss the state-of-art simulators used to test and validate autonomous driving solutions. Furthermore, the comparison of some additional commercial and open-source simulators is also presented in

Table 2. Comparison of Autonomous Driving Simulators.

Features		Simulator
		CARLA	AirSim	DeepDrive	LGSVL	NVIDIA Drive	rFpro	MATLAB	Gazebo
General	Licence	Open-Source	Open-Source	Open Source	Open-Source	Commercial	Commercial	Commercial	Open-Source
	Portability	Windows and Linux	Windows and Linux	Windows and Linux	Windows and Linux	Windows and Linux	Windows and Linux	Windows and Linux	Windows and Linux
	Physics Engine	Unreal Engine	Unreal Engine and Unity	Unreal Engine	Unity	Unreal Engine	U	Unreal Engine	DART
	Scripting Languages	Python	C++, Python, Java	C++, Python	Python	Python	U	MATLAB	C++, Python
Environmental	Urban Driving	Town	Town, City	Road Track	City	City, Harbor	Town, City, Road Track	N	Road Track
	Off-Road	N	Forest, Mountain	N	N	N	N	N	N
	Actors–Human	Y	N	N	Y	N/A	Y	Y	Y
	Actors–Cars	Y	Y	Y	Y	N/A	Y	Y	Y
	Weather Conditions	Y	Y	Y	Y	Y	Y	N	N
Sensors	RGB	Y	Y	Y	Y	Y	Y	Y	Y
	Depth	Y	Y	Y	Y	N/A	Y	N	N
	Thermal	N	Y	N	N	N/A	N/A	N	Y
	LiDAR	Y	Y	N	Y	Y	Y	Y	Y
	RADAR	Y	N	N	Y	Y	Y	Y	Y
Output Training Labels	Semantic Segmentation	Y	Y	N	Y	Y	Y	Y	Y
	2D Bounding Box	Y	N	N	Y	Y	N/A	Y	Y
	3D Bounding Box	Y	N	Y	Y	N/A	N/A	Y	Y

.

• MATLAB/Simulink: launched its Automated Driving Toolbox which offers various tools and algorithms to facilitate the design, simulation, and testing of Advanced Driver Assistance Systems (ADAS) and automated driving. It enables the users to test its main functionalities such as environment perception, path planning, and vehicle control. It provides the feature to import HERE HD live map data and OpenDRIVE^® road networks into MATLAB and can be used for various design and testing applications. Last but not least, the toolbox allows the development of C/C++ code for faster prototyping and Hardware-in-the-Loop (HIL) testing, providing support for sensor fusion, tracking, path planning, and vehicle controller algorithms.
• PreScan: an open-source physics-based simulation platform that aims to design ADAS and autonomous vehicles. It introduces PreScan’s automated traffic generator, which offers manufacturers a variety of realistic environments and traffic conditions to test their autonomous navigation solutions. It can also be used to design and evaluate V2V and vehicle-to-infrastructure (V2I) communication applications. Among other features, it also provides support for HIL simulation, real-time data, and Global Positioning System (GPS) vehicle data recording, which can then be replayed later. Furthermore, PreScan provides a special function known as the Vehicle Hardware-In-the-Loop (VeHIL) laboratory. The test/ego vehicle is set up on a rolling bench, and other vehicles are represented by wheeled robots that resemble vehicles allowing users to establish a hybrid real-virtual system. Real sensors are installed in the test vehicle. Therefore, the VeHIL is capable of offering thorough simulations for ADAS by utilizing this setup of ego vehicles and mobile robots.
• LGSVL: an open-source multi-robot autonomous driving simulator developed by LG Electronics America R&D Center. It is built on the Unity game Engine and offers various bridges to pass the message between the autonomous driving stack and the simulator backbone. The simulation engine provides different functions to simulate the environment (e.g., traffic simulation and physical environment simulation), sensor simulation, and vehicle dynamics. Additionally, a PythonAPI is available to control various environmental variables, such as the position of the adversaries, the weather, etc. Furthermore, it also provides a Functional Mockup Interface (FMI) to integrate the vehicle dynamics model platform with the external third-party dynamics models. Lastly, exporting high-definition (HD) maps from 3D settings is one of the key capabilities of LGSVL.
• Gazebo: a multi-robot, open-source, scalable, and flexible 3D simulator that enables the simulation of both indoor and outdoor environments. The world and model are the two fundamental elements that make up the 3D scene. The gazebo is comprised of three main libraries which include physics, rendering, and communication library. In addition to these three core libraries, it also provides plugin support that enables the users to communicate with these libraries directly. The gazebo is renowned for its great degree of versatility and its smooth Robot Operating System (ROS) integration. High flexibility has its benefits because it provides users with complete control over the simulation, but it also requires time and effort. In contrast to CARLA and LGSVL simulators, Gazebo requires the user to construct 3D models and precisely specify their physics and location in the simulated world within the XML file. This manual approach is how simulation worlds are created in Gazebo. It provides a variety of sensor models but also allows users to add new ones by using plugins. Moreover, Gazebo is extremely well-liked as a robotic simulator, but the time and effort required to construct intricate and dynamic scenarios prevent it from being the first choice for testing self-driving technology. The gazebo is a standalone simulator but most often it is used with ROS.
• CarSim: a vehicle simulator that is frequently used in both academics and industry. The latest version of it supports moving objects and sensors that are useful for simulations involving ADAS and autonomous vehicles. These moving items, such as vehicles, cyclists, or people, can be connected to 3D objects with their embedded animations. The key advantage of CarSim is that it offers interfaces for other simulators such as MATLAB and LabVIEW. CarSim is not an open-source simulator, but it does have extensive documentation and provides several simulation examples.
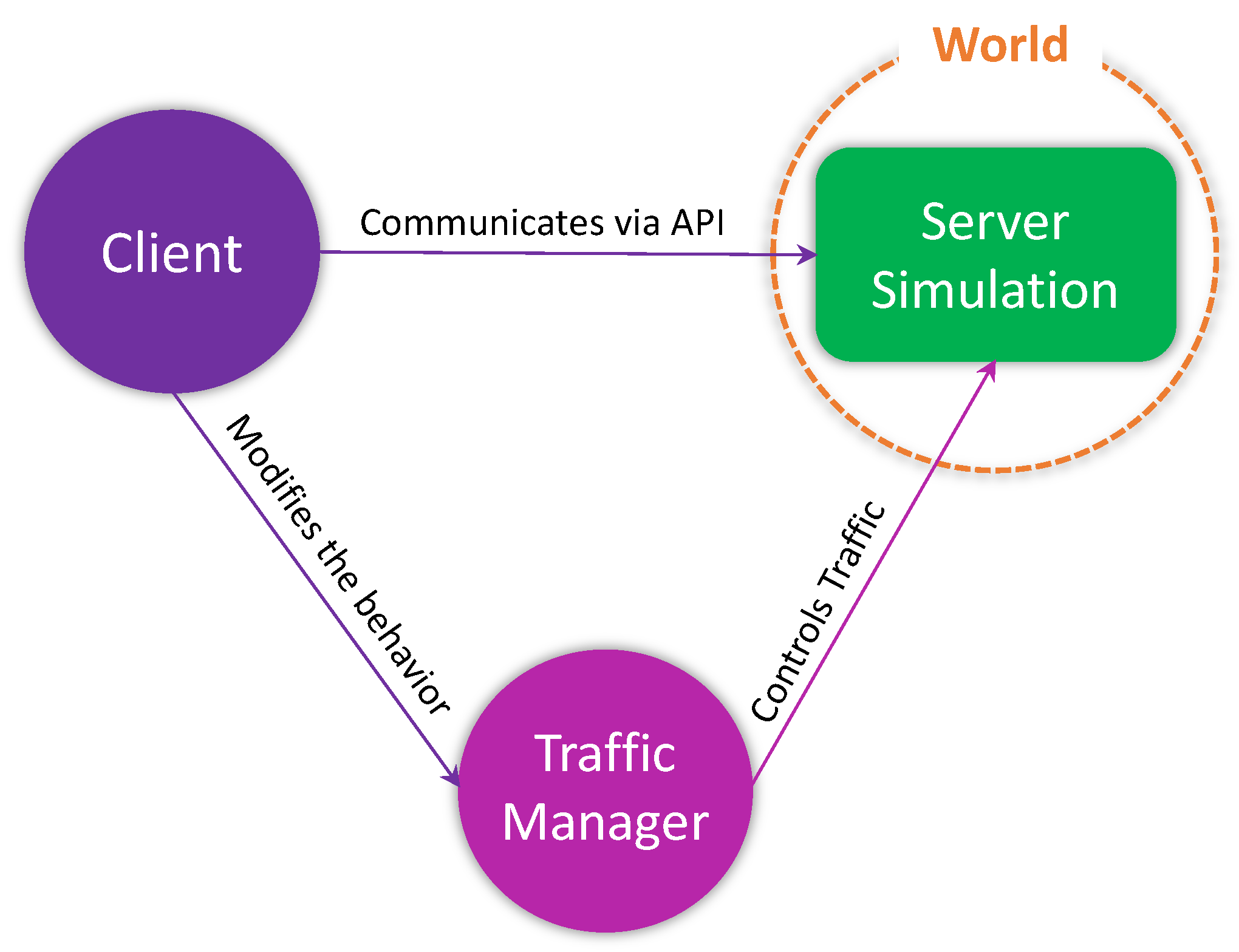
• CARLA [8]: an open-source simulator for autonomous urban driving. It is developed from scratch to support training, prototyping, and validation of autonomous driving solutions including both perception and control. As a result, CARLA makes an effort to meet the needs of different ADAS use cases, such as learning driving rules or training the perception algorithms. It is comprised of a scalable client-server architecture that communicates over transmission control protocol (TCP). It simulates an open, dynamic world implementing an interface between the world and an agent which interacts with the world. The server is responsible for running the simulation, rendering the scenes, sensor rendering, computation of physics, providing the information to the client, etc. Whereas, the client side is comprised of some client modules that aim to control the logic of agents appearing in the scenes. For a detailed discussion on CARLA, the readers are encouraged to look into the authors’ previous publication [9].

A simulator should be as realistic as possible. Thereby, this means it should be accurate with lower-level vehicle calculations such as the physics of the vehicle and detailed in terms of the 3D dynamics and surroundings. There is always a trade-off between the accuracy of the 3D environment and the vehicular dynamics [9]. To choose the right simulator, several factors can be used as a metric to determine which simulators are most appropriate for different tasks. These factors may include a set of sensors to create environmental perception, complex dynamics of the environment, multi-view geometry, traffic infrastructure, vehicle control, traffic scenario simulation, 3D virtual environment, 2D/3D ground truth, and last but not least, open source. We analyze that MATLAB/Simulink is built with effective plot features and computation capabilities to simulate straightforward scenarios. PreScan, as opposed to MATLAB and CarSim, offers superior capabilities to create realistic surroundings and simulate various weather situations. Although the Gazebo is a well-known 3D robotic simulator, testing autonomous driving technology is not the best use for it due to the time and effort required to generate sophisticated and dynamic scenarios. Therefore, we shortlisted two simulators: LGSVL and CARLA. They are the best simulators for testing perception, mapping, vehicle control, and localization systems for autonomous vehicles. The majority of their characteristics are similar, e.g., open-source, portability, 2D/3D ground truth, flexible API, etc., however, the LGSVL does not offer camera calibration to conduct multi-view geometry or Simultaneous Localization and Mapping. In that sense, we decided to choose the CARLA simulator for this research.

3.2. Relevant Studies

Gómez-Huélamo et al. [10] validated the fully autonomous driving architecture in the CARLA based on some challenging driving scenarios inspired by the CARLA Autonomous Driving Challenge (CADC), focusing on the proposed decision-making layer, based on Hierarchical Interpreted Binary Petri Nets (HIBPN). They started by outlining the ROS-based autonomous driving architecture. The CARLA simulator is then discussed, along with the steps followed to integrate the suggested architecture with it and the benefits of developing ad-hoc driving scenarios for use case validation. The architecture was then evaluated utilizing some driving conditions, including STOP, Pedestrian Crossing, ACC, and Unexpected Pedestrian. For each use case, some qualitative and quantitative findings were reported, verifying the architecture in the simulation. In another study [11], the authors extended their work with several interesting temporal graphs to examine the sequence of events and its effect on the physical behavior of the vehicle holistically.

Ramakrishna et al. [12] conducted interesting research and proposed an ANTI-CARLA framework for automated adversarial testing, evaluation, and exploration of the performance of AVs within the CARLA simulator. It offers a framework that enables the plugging in and testing of any pipeline for autonomous driving. It is comprised of a domain-specific Scenario Description Language (SDL) to explain the test conditions and a simple interface to specify test conditions. The suggested system has the drawback of only being able to sample static scenes. The temporal order of scenes preceding each failed case, however, is not yet available.

To enhance the accuracy of risk assessment for autonomous vehicles, leveraging situational awareness for behavior prediction, Reich et al. [13] developed the Situation-Aware Dynamic Risk Assessment (SINADRA) method. They created a computing pipeline as a Python program element and integrated it into the CARLA. Based on dynamically monitored environmental cues, SINADRA employed probabilistic Bayesian network models to estimate the behavior intentions of other traffic participants. Afterward, these behavior intentions were converted into trajectory distributions by using behavior-specific motion models. Finally, probabilistic risk metrics evaluated the risk of executing the planned ego trajectory in the current scenario given the expected future positions of traffic participants and a planned ego trajectory.

The systematic testing of autonomous vehicles operating in a complex real-world environment is a challenging and costly problem. Therefore, to tackle this issue, Majumdar et al. [14] developed a Paracosm framework allowing users to write systematic test scenarios for autonomous driving simulations. It enables users to programmatically define complicated driving scenarios with particular elements, such as road layouts, environmental conditions, and temporal reactions of other vehicles, and pedestrians. It is also made practicable to explore the state space systematically for both visual elements and reactive interactions with the environment. Additionally, a notion of test coverage for parameter configurations is defined based on combinatorial testing and low dispersion sequences.

Vukic et al. [15] developed an urban-like neighborhood simulation environment based on Unity to test sensors and algorithms for autonomous vehicles and to show the deviations from reference data. The proposed simulation model comprised city objects and participants such as roads, sidewalks, buildings, pedestrians, traffic signs, and vehicles. They simulated the motion and sensors from a single vehicle equipped with a stereo camera setup. Unity was used to design the simulation; however, the behavioral scripts were executed using the C# programming language. The OpenCV class for computing stereo correspondence employing the semi-global block matching algorithm was applied to simulate stereo images to demonstrate the testing of relevant algorithms.

The simulation framework proposed by Teper et al. [16] integrated cutting-edge robotics, communication, and control system components such as ROS2, Gazebo, OMNeT++, Artery, MATLAB, and Simulink to simulate the cooperative autonomous driving scenarios and their required technologies. The proposed framework can also be used to integrate new tools since the integration is done in a modular fashion. The platooning scenario under cooperative adaptive cruise control (CACC) and the ETSI ITS-G5 communication architecture was used by the authors to further highlight the framework.

In another study, Cai et al. [17] presented SUMMIT, a simulator to generate high-fidelity interactive data to develop, train, and test crowd-driving algorithms. The simulator generated unregulated congested traffic at any location in the world using online maps. It could generate complex and realistic crowds that closely resemble uncontrolled traffic in the real world by fusing topological road contexts with an optimization-based crowd behavior model. Moreover, the authors also formulated a Context-POMDP as a reference planning algorithm for future developments. In conclusion, they stated that SUMMIT can support a wide range of applications such as perception, control, planning, and learning for driving in unregulated dense urban traffic.

Emre et al. [18] addressed the problem of tracking algorithms based on deep learning. To this end, they designed and developed four different deep learning algorithm—deep convolutional neural networks, deep convolutional neural networks with fine-tuning, transfer learning with a deep convolutional neural network, and fine-tuning deep convolutional neural networks with transfer learning to track the targeted object. The proposed algorithms achieved significantly good results than the state-of-the-art algorithms. In another research, Gulay [19] worked on a similar problem. They leveraged the Kalman filter and deep learning algorithms to detect and track the multiple dynamic targeted objects.

4. Proposed Extension to CARLA

In this section, we provide a detailed discussion of the design and development of CARLA+. In what follows next, we first discuss the PGM for modeling the environment followed by a thorough discussion on the design and development of CARLA+ which integrates a PGM framework with CARLA.

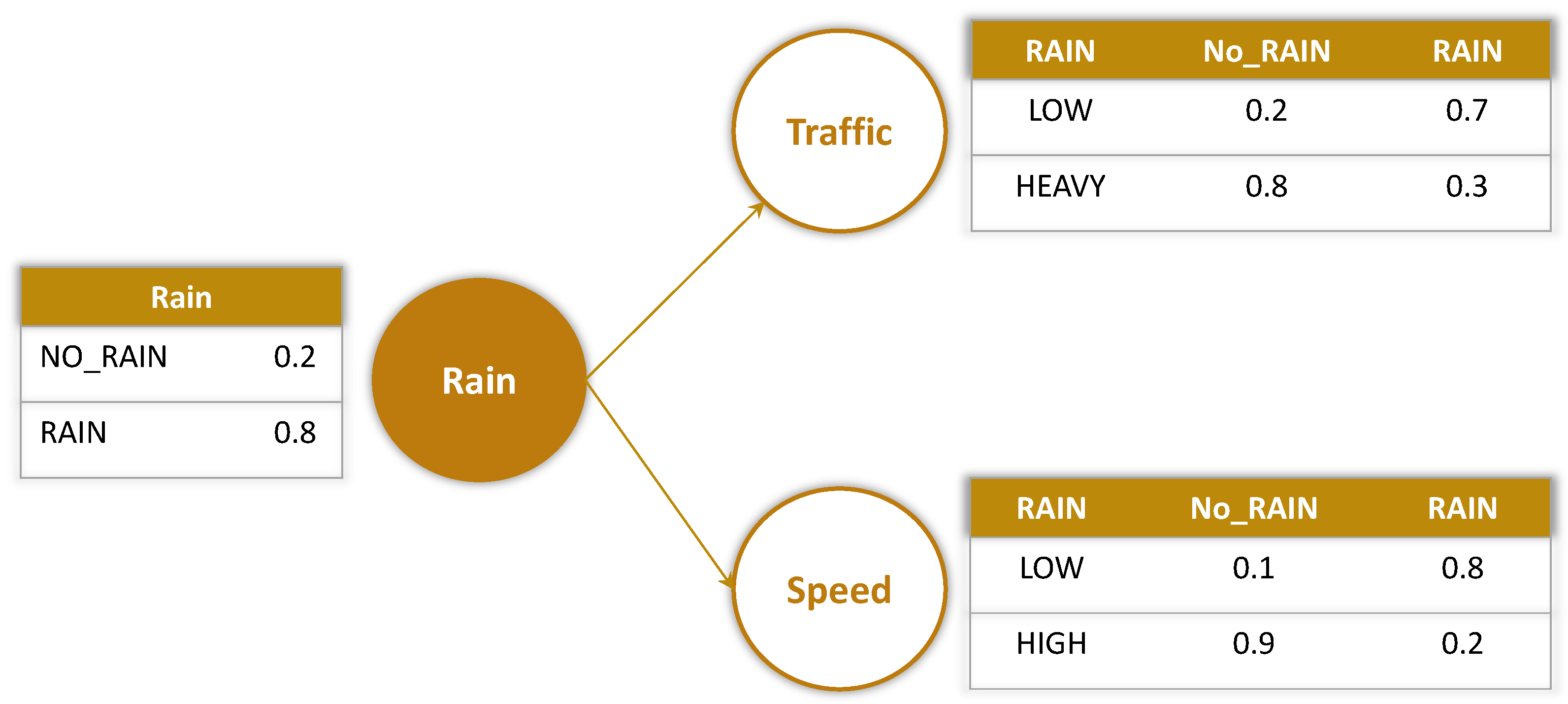
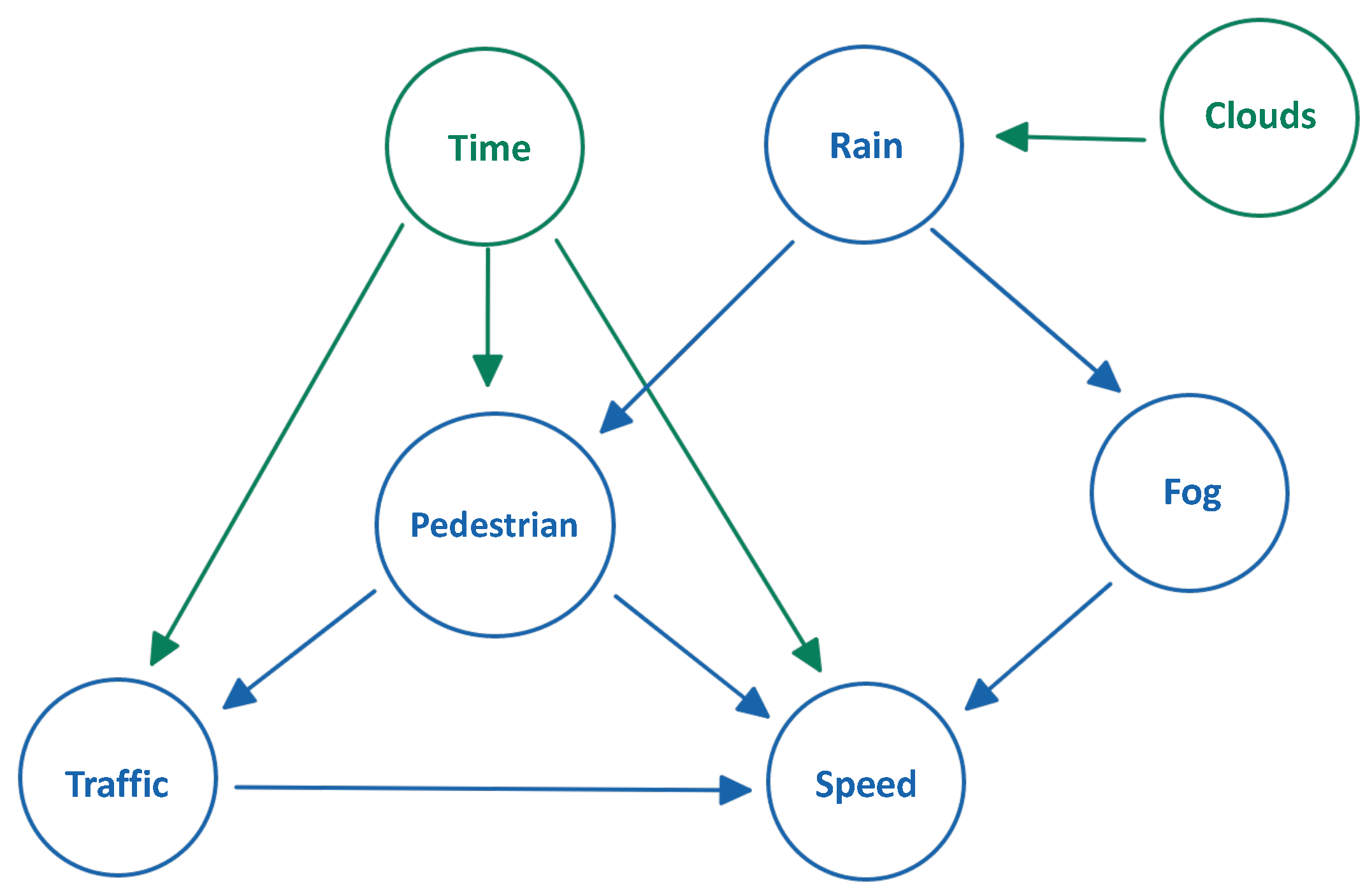
4.1. PGM for Modeling Complex Urban Environment

To capture the realistic dynamics of the complex urban environment such as the number of vehicles, the dynamic speed of the vehicles, the probability of pedestrians in an urban environment, the dynamic weather of the environment, and the time of the day, the probabilistic graphical model (PGM) is used. We aim at capturing the dynamically changing state of the environment, the partially observable state of the environment, and unprecedented events in the environment. To further understand the environment, consider Figure 1 which explains some scenario scenes of the complex urban environment.

In what follows next, we discuss the motivation to opt for the PGM, which comes from the following facts:

• It is instrumental in understanding the complex relationship between a set of random variables. This is an important feature because the considered problem domain involves several variables (e.g., number of vehicles, number of pedestrians, vehicle speed, weather state, time of the day, distance from other vehicles and objects, road markings, road signs, road traffic lights, etc.) Furthermore, these variables have an impact on one another, resulting in much more complex interparameter relationships;
• It allows to reuse the knowledge accumulated over the different scenes and settings;
• It allows for solving tasks such as inference learning. This feature is relevant to the considered collaborative autonomous driving problem domain since we are interested in estimating the probability distributions and probability functions in different use cases. For instance, when the probability is associated with the elements of action space in a specific use case, we are interested in achieving the optimal values of the associated probability values;
• It allows the independence properties to represent high-dimensional data more compactly. The independence properties help in the considered problem domain by assisting in understanding the characteristics of a particular attribute separately from the rest of the system;
• The concept of conditional independence brings in significant savings in terms of how to compute and represent the network structure.

A PGM models a joint probability distribution over a set of random variables $\mathbf{X}=\left\{X_1,...,X_n\right\}$. It is represented as a pair $(\mathcal{G},{\Theta })$, which consists of a graph structure $\mathcal{G}$ that codifies the dependent relationships between the random variables and a set of parameters ${\Theta }$. There are different types of PGM models, however, in this research, we implement the PGM model based on directed acyclic graphs (DAG). Given a PGM $(\mathcal{G},{\Theta })$ with a DAG $\mathcal{G}=(\mathbf{X},\mathbf{R})$, where X is a non-empty finite set of nodes and R is a set of edges, and three distinct subsets of variables $(\mathbf{U},\mathbf{Y},\mathbf{Z})$ of $\mathbf{X}$, $\mathbf{Y}$ is conditionally independent of $\mathbf{Z}$ given $\mathbf{U}$ if $\mathbf{U}$ d-separates $\mathbf{Y}$ and $\mathbf{Z}$ in $\mathcal{G}$.

We suppose that the set of variables $\mathbf{X}$ is arranged in accordance with a DAG $\mathcal{G}$ ancestral ordering, the parent nodes of $X{}_j\left({\mathbf{PA}}_j\right)$ variable d-separates $X_j$ from any prior variable in the ancestral ordering, $X_i\left(i<j\right)$. This is to say that $X_j$ is conditionally independent of any $X_i\left(i<j\right)$ given its parents, ${\mathbf{PA}}_j$. Based on this property, we express the joint probability distribution of $\mathbf{X}$ given the chain rule as:

$$\begin{array}{c}\hfill p\left(x\right)=p\left(x_1,...,x_n\right)=\prod _{j=1}^{n}p\left(x_j\mid x_1,...,x_{j-1}\right)\end{array}$$

(1)

when codified by a DAG-based PGM, it is factorized as:

$$p\left(x\right)=\prod _{j=1}^{n}p(x_j\mid {\mathbf{pa}}_j)$$

(2)

Bayesian network (BN) models are DAG-based PGMs with all the discrete random variables, comprised of a DAG $\mathcal{G}$ and a set of parameters ${\Theta }$. By taking DAGs into account, the joint probability distribution $p\left(x\right)$ can be factored using Equation (2), which typically uses a much smaller set of ${\Theta }$ than the general factorization (Equation (1)). The set of parameters ${\Theta }$ represents all the probability distributions, $p\left(x_{jl}\mid {\mathbf{pa}}_{jk}\right)$. Each parameter ${{\Theta }}_{jkl}=p\left(x_{jl}\mid {\mathbf{pa}}_{jk}\right)$ defines the probability that variable $X_j$ takes its $l-th$ possible value given that the parents ${\mathbf{PA}}_j$ of $X_j$ take their $k-th$ value. Each variable $X_j$ has a set of $d_j$ values. As a result, the set of potential values for a random vector is the product of the sets of possible values for each X such that the parent ${\mathbf{PA}}_j$ of variable $X_j$ takes $D_j={\prod }_{i/X_iϵ{\mathbf{PA}}_j}{d}_i$ different values.

As the size of the model increases, the BN model derived from a set of examples becomes impractical. Therefore, we learn the BN. Generally, the process of learning a BN with DAG $\mathcal{G}$ and parameters ${\Theta }$ from a data set $\mathcal{D}$ comprising n observations can be accomplished in two steps, Equation (3). Following the $\mathcal{D}$ provision, the BN is learned in two stages: structural learning and parametric learning.

$$\underset{\mathrm{Learning}}{\underbrace{P(\mathcal{G},{\Theta }\mid \mathcal{D})}}=\underset{\mathrm{Structure}\mathrm{Learning}}{\underbrace{P(\mathcal{G}\mid \mathcal{D})}}·\underset{\mathrm{Parameter}\mathrm{Learning}}{\underbrace{P({\Theta }\mid \mathcal{G},\mathcal{D})}}$$

(3)

Finding the $\mathcal{G}$ that encodes the dependent structure of the data constitutes structure learning. In this research, we opt for the Hill Climbing (HC) search algorithm to learn the structure of the BN. In Algorithm 1, the initialization phases (steps 1 and 2) are followed by an HC search (step 3). HC executes local moves such as arc additions, deletions, and reversals to explore the area around the current candidate ${\mathcal{G}}_{max}$ in the space of all possible DAGs aiming to locate the $\mathcal{G}$ (if any) that raises the score Score $(\mathcal{G},\mathcal{D})$ the most over ${\mathcal{G}}_{max}$. Then, in each iteration, the HC attempts to add each potential arc that is not already present in ${\mathcal{G}}_{max}$, as well as to delete and reverse each arc in the current optimal ${\mathcal{G}}_{max}$. For all the remaining acyclic DAGs ${\mathcal{G}}^{*}$, the HC calculates $S_{{\mathcal{G}}^{*}}$ = $Score$$({\mathcal{G}}^{*},\mathcal{D})$. The new candidate $\mathcal{G}$ is the ${\mathcal{G}}^{*}$ with the highest $S_{{\mathcal{G}}^{*}}$. If this DAG has $S_{\mathcal{G}}>S_{max}$, then $\mathcal{G}$ becomes the new ${\mathcal{G}}_{max}$, and $S_{max}$ is set to $S_{\mathcal{G}}$ and HC moves to the next iteration. On the other hand, if $S_{\mathcal{G}}<S_{max}$, the HC reaches an optimum.

Algorithm 1. Hill-climbing search algorithm for structure learning

Input: a dataset $\mathcal{D}$ from X, an empty DAG $\mathcal{G}$, a score function Score $(\mathcal{G},\mathcal{D})$.   Output: the ${\mathcal{G}}_{max}$ that maximizes the Score $(\mathcal{G},\mathcal{D})$. 1: Compute the score of $\mathcal{G}$, $S_{\mathcal{G}}$ = $Score$$(\mathcal{G},\mathcal{D})$ 2: Set $S_{max}=S_{\mathcal{G}}$ and ${\mathcal{G}}_{max}=\mathcal{G}$ 3: Hill Climbing: repeat as long as $S_{max}$ increases. (a) For each potential arc addition, deletion, or reversal in ${\mathcal{G}}_{max}$ resulting in a DAG:    (i) Compute the score of updated ${\mathcal{G}}^{*}$, $S_{{\mathcal{G}}^{*}}$ = $Score$$({\mathcal{G}}^{*},\mathcal{D})$    (ii) $S_{{\mathcal{G}}^{*}}>S_{max}$ and $S_{{\mathcal{G}}^{*}}>S_{\mathcal{G}}$, then set $\mathcal{G}={\mathcal{G}}^{*}$ and $S_{\mathcal{G}}=S_{\mathcal{G}}*$ (b) If $S\mathcal{G}>S_{max}$, set $S_{max}=S_{\mathcal{G}}$ and ${\mathcal{G}}_{max}=\mathcal{G}$

As a local search algorithm, the HC can get stuck in the local optima. Therefore, there are two simple approaches that are efficient to escape from the local optima:

• Tabu List: it first moves away from ${\mathcal{G}}_{max}$ by allowing up to $t_0$ additional local moves. These moves would generate DAGs ${\mathcal{G}}^{*}$ with $S_{{\mathcal{G}}^{*}}\le S_{max}$, therefore, the new candidate DAGs would have the highest $S_{\mathcal{G}}$ even though if $S_{\mathcal{G}}<S_{max}$. Moreover, DAGs accepted as candidates in the last $t_i$ iterations would be saved in a list referred to as the tabu list. It will allow the algorithm to not revisit the recently seen structures aiming to guide the search towards unexplored regions of the space of the DAGs and this approach is referred to as Tabu search.
• Random Restarts: multiple restarts up to r times would allow the algorithm to find the global optimum when at a local optimum.

Estimating the ${\Theta }$ based on the $\mathcal{G}$ produced by structure learning is what parameter learning entails. We employ the Bayesian Parameter Estimation to learn the parameters. When learning with a Bayesian approach, the Dirichlet distribution is used as an a priori distribution over all possible sets of parameters, and the maximum a posteriori probability (MAP) estimation—the set of parameters $\widehat{{\Theta }}$ with the highest a posteriori probability given the $\mathcal{D}$ and a graph structure $\mathcal{G}$—is used to estimate the parameters.

$$\widehat{{\Theta }}=arg\underset{{\Theta }}{max}p({\Theta }\mid \mathcal{G},\mathcal{D})\alpha arg\underset{{\Theta }}{max}p(\mathcal{D}\mid \mathcal{G},{\Theta }).p(\mathcal{G},{\Theta })$$

(4)

Given a set of hyper-parameters $\alpha =({\alpha }_{jk1},...,{\alpha }_{jk{d}_j})$, which are the parameters of the a priori Dirichlet distribution that characterizes the prior knowledge about the $\widehat{{\Theta }}$, we compute the set of $\widehat{{\Theta }}$ that maximizes this expression by using the formula below:

$$\widehat{{{\Theta }}_{jkl}}=\frac{N_{jkl}+{\alpha }_{jkl}}{N_{jk}+{\alpha }_{jk}}$$

(5)

where in Equation (5), the $N_{jkl}$ is the total number of occurrences in $\mathcal{D}$ where the variable $X_j$ is given its $l-th$ value and the configuration of ${\mathbf{PA}}_j$ is given its $k-th$ instance, $N_{jk}={\sum }_{l=1}^{d_j}{N}_{jkl}$ and ${\alpha }_{jk}={\sum }_{l=1}^{d_j}{\alpha }_{jkl}$.

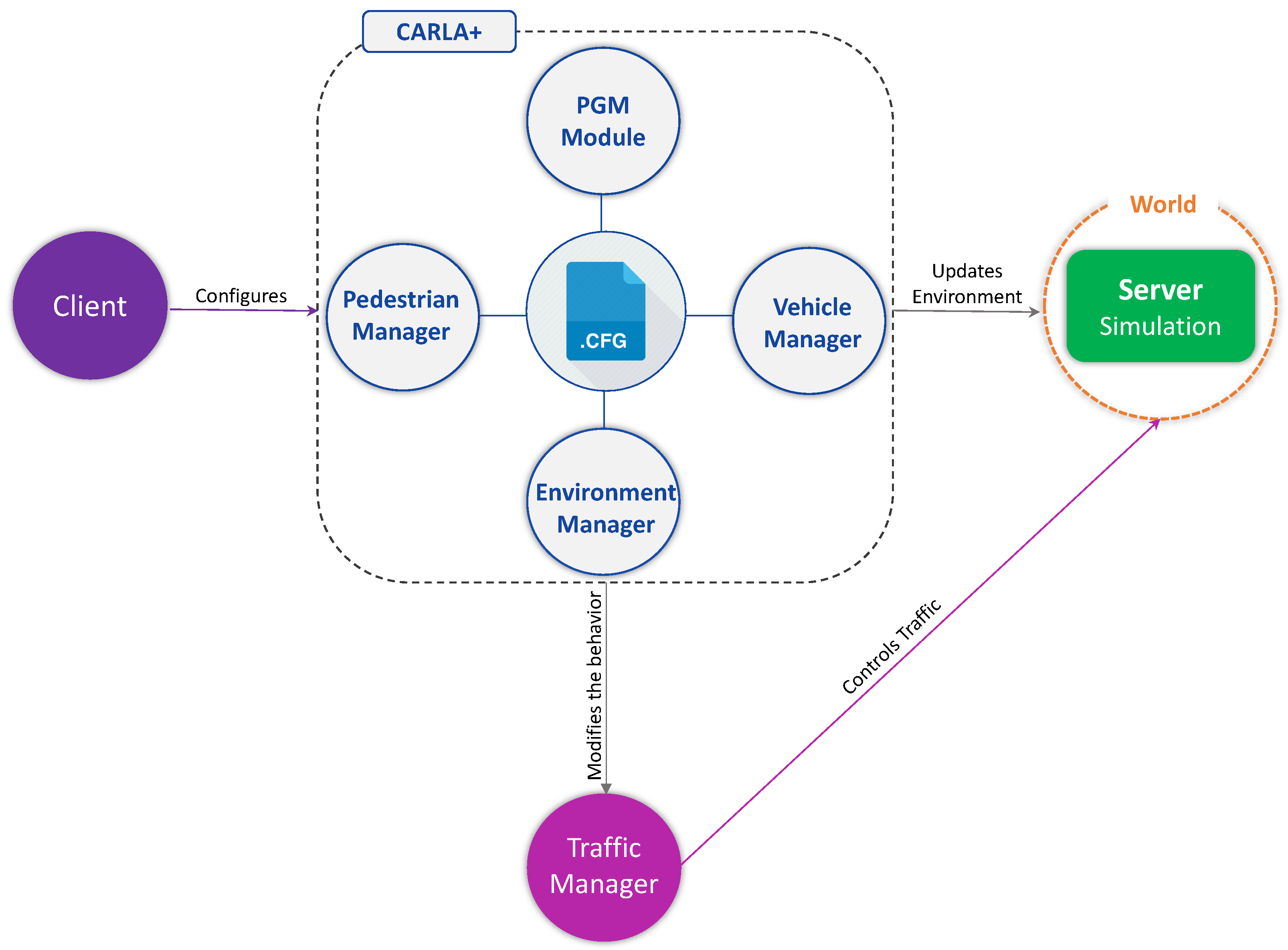
4.2. Designing CARLA+

This section presents a detailed discussion on designing the CARLA+ comprises various crucial components. In what follows next, we discuss each component in detail.

4.2.1. CARLA Architecture

CARLA utilizes the client-server model for its operation where the server runs the actual simulation and the client is responsible to communicate and controlling that simulation. The CARLA client communicates with the CARLA server using the provided API. Therefore, to use the CARLA client, we first establish a connection with the CARLA server running on a specific IP and port. Multiple clients can also be used to communicate simultaneously with a server. The main functionality of the client is to ask for information from the server, load different maps, record simulations, and initialize the traffic manager. The classical architecture of CARLA is presented in Figure 2.

In CARLA, the World represents an object, encapsulating the actual simulation. It is an abstract layer that is used to spawn different actors (vehicles, pedestrians, etc.), change weather conditions, obtain the current state of the world, etc. Each simulation will contain only one world object, which will be destroyed and replaced when loading a new map.

CARLA also provides a Traffic Manager module which controls vehicles in autopilot mode. This is the default implementation for traffic simulation in CARLA. Its behaviors can be modified by the user/client, e.g., forcing a lane change, over-speeding, ignoring traffic lights, stopping signs, etc. It can be used to orchestrate carefully designed driving scenarios to train autonomous agents.

Actors are those elements in CARLA that can perform some action to affect the environment or other actors. These include different sensors, traffic signs, traffic lights, vehicles, pedestrians, etc. These actors can be spawned, handled according to the requirements, and destroyed, by the World. Sensors are special actors that are used to retrieve data from their surroundings.

4.2.2. Maps

In CARLA, a map consists of both the 3D model of the town and the road definition. CARLA comes with 8 predefined towns, each containing two kinds of maps, layered and non-layered maps. Layered maps allow the user to toggle certain layers of the maps, such as buildings, etc., while non-layered maps do not allow any layer-toggling. Furthermore, new user-defined maps can be created and imported into CARLA, allowing for more customizability and extensibility of the system. The proposed CARLA+ is designed in a way that it can work with any kind of map either built-in or user-defined. This would retain the extensibility of the CARLA environment while providing the option for a more realistic and dynamic environment modeling irrespective of the map.

4.2.3. Vehicles

There are a number of blueprints for different types of vehicles in the CARLA. A blueprint is a predefined model with animations and attributes, some of which are modifiable. They allow for the easy incorporation of new actors into the simulation. CARLA contains 70+ blueprints for a different types of vehicles and pedestrians, from large trucks to motorcycles. The proposed CARLA+ allows the user to spawn a particular vehicle based on its blueprint ID, select a vehicle at random, or filter vehicles using a wildcard pattern, e.g., using the pattern ’vehicle.mercedes.*’ would return all the available models of mercedes. Furthermore, CARLA+ uses all kinds of vehicles by default, but the user can configure if they want to experiment with a particular type of vehicle or a particular model.

4.2.4. Weather

Each town is loaded with suitable weather, which can be customized based on user requirements. Different weather parameters can be set by using the WeatherParameters class to simulate a particular weather. These parameters are independent of each other, i.e., having more clouds would not automatically result in rain or raining would not automatically create puddles as well. Some of the parameters that can be set are cloudiness, precipitation, wind intensity, fog, sun azimuth, altitude angles, etc. CARLA+ enables the user to validate their solutions in any weather setting. Some of the examples of weather conditions in CARLA are shown in Figure 3.

4.3. Developing CARLA+

In this section, we discuss the development of CARLA+ and its components. The proposed high-level architecture of CARLA+ is presented in Figure 4.

The CARLA+ is comprised of four main modules:

• Environment Manager Module;
• Vehicle Manager Module;
• Pedestrian Manager Module;
• Integration of PGM Module.

Each of these modules is configured via configuration files, which contain different specifications for environment modeling. The configuration files are an integral piece of the framework as they connect all the other modules together and allow them to function seamlessly. These files are defined in a hierarchical manner where the underlying config can easily be replaced with a different one based on the scenario and requirements. Figure 5 shows the different configuration files, their folder structure, as well as some sample configs to demonstrate how they are used within CARLA+. Configurations within a particular directory are easily replaceable with another of its peers. For example, to load rainy weather instead of clear, we can easily specify the weather/rain.yaml file in the main config file. Schema definitions for different types of configurations are also defined to make sure that the user-defined config files conform to the schema definitions. All of these configuration files are modifiable at three levels, i.e., using the actual config files, using the command line, as well as the Python script.

In what follows next, we discuss the functionality and role of each component in detail.

4.3.1. Environment Manager Module

This module deals with the configuration of the simulation environment. It is developed to dynamically simulate the weather and time of day. Based on the provided configuration files, it changes the weather and time inside the simulated environment. It can also dynamically change the weather with the passage of time. The configuration files expose a number of parameters such as cloudiness, rain, wind, fog, etc., where the user can specify the percentage of value required to get the desired weather in the environment. Some of the pre-defined weather configuration files for some common scenarios, such as clear, rainy, cloudy, etc., are also provided. Furthermore, we enable the user to model a particular hour of the day which can automatically be converted into respective sun azimuth and altitude angles to be used in the simulation. All of these configuration files are configurable and can be extended by the researchers allowing for more granular control over every aspect of the simulation environment.

4.3.2. Vehicle Manager Module

This module is developed to adjust the behavior of the traffic inside the simulation. It allows for a wide range of configuration parameters for traffic, such as the number of vehicles to spawn, the maximum allowed speed, the safe distance from the leading vehicle, the type of vehicle to spawn, and more. Each of these parameters can be configured via configuration files and can be modified later on by the PGM model based on the state of the world. The user can also choose to spawn a mixed type of vehicle such as a car, van, truck, etc.

4.3.3. Pedestrian Manager Module

This component is developed to capture the dynamics of the pedestrians in the simulation environment. It manages the number of pedestrians to spawn, and randomly spawns them on various locations around the map. It also provides the functionality to modify the behavior of the spawned pedestrians, such as the percentage of pedestrians that are running or crossing the road, etc. This module can be used to dynamically model the number and behavior of pedestrians in specific scenarios such as roundabouts. We also provide multiple pedestrian models enabling users to spawn various types of pedestrians which can easily be configured via the configuration files provided.

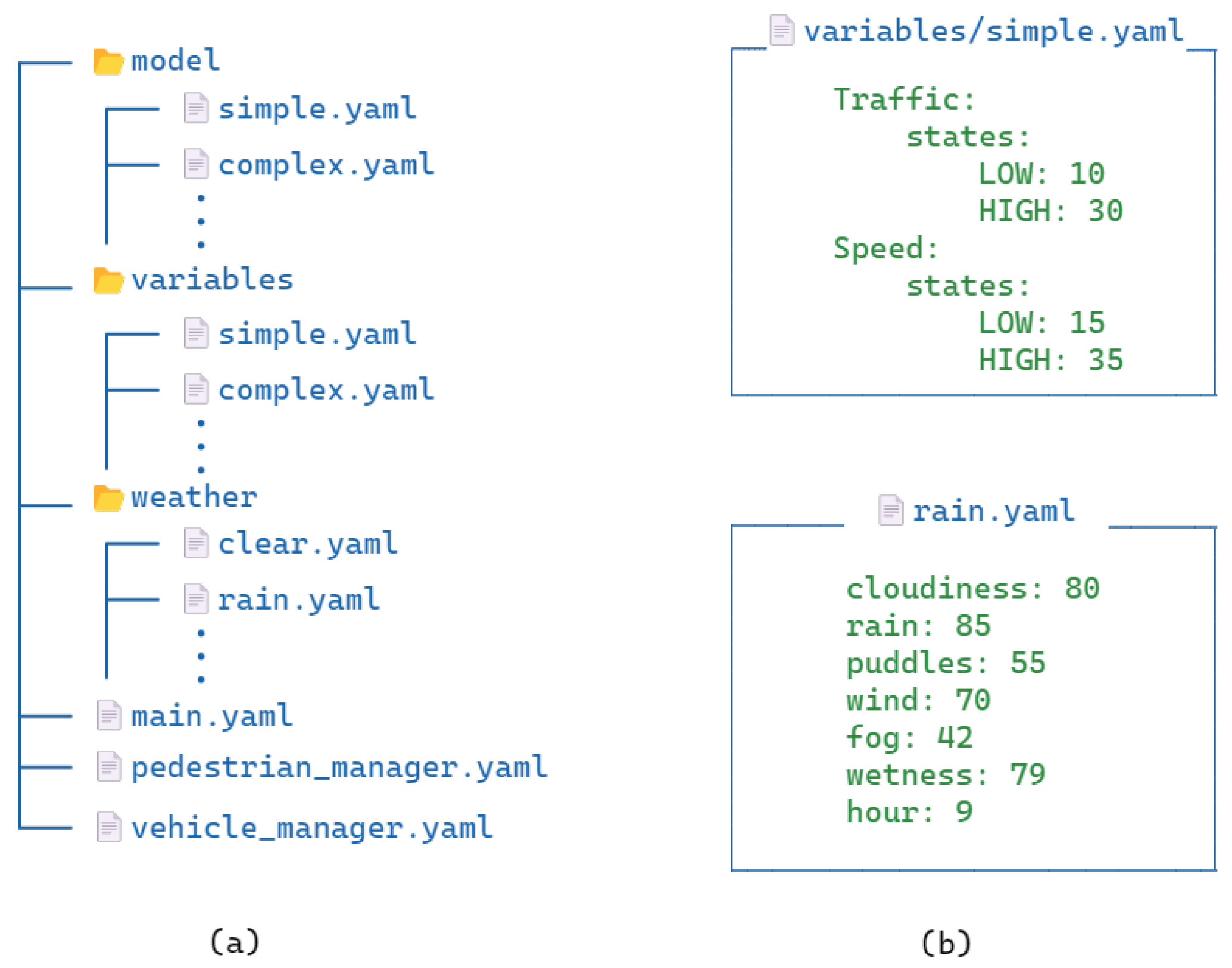
4.3.4. Integrating PGM Module

This is the main component of the CARLA+ that glues all the other components together. It takes the current state of the world as input and predicts the state of different variables based on that. It uses a BN model and loads the Conditional Probability Distribution (CPD) from the configuration files. It then uses the Variable Elimination method to obtain the probability distribution of the required states. The simulated environment is then updated based on the most probable state of the desired variables.

This module is developed to be used in a number of ways. First, the states and CPDs of different variables can be defined entirely in the configuration files manually. The module will create a BN model based on those configuration files. Second, different parameter learning algorithms can be used to directly learn the CPDs of variables from raw data, which can then be exported into the configuration files and loaded into a BN from there. Another approach could be to bypass the configuration files for CPDs and directly load or train the BN when the simulation starts. This flexibility allows us to handle various scenarios, from hand-crafted CPDs to complex CPDs learned directly from real-world data.

Once the model and its CPDs are defined, the CARLA+ loads that model into memory and use that for modeling the simulation. The CARLA client queries the CARLA server for different environmental parameters, and based on the returned parameters, it uses the user-defined PGM model to infer new states for different variables. Once the desired states have been calculated, CARLA+ updates the simulation weather in the CARLA server and traffic count as well as a behavior using the Traffic Manager accordingly. In this way, the CARLA+ framework extends the classical CARLA by integrating it with a PGM framework that is able to model different parameters in the simulated environment and dynamically change the states of those variables based on their dependencies, as defined in the CPD.

Having discussed the design and development of CARLA+, we provide a discussion on clearly highlighting the difference between the classical CARLA and CARLA+. Although CARLA is a comprehensive and well-designed simulator for autonomous driving, providing options to customize the environment including the map, number, and type of vehicles, pedestrians, weather and time of day, automatic and manual traffic control, etc., it does not provide a unified framework to automatically manage those. For instance, we can manually code to spawn a different number of pedestrians based on weather conditions and daytime using multiple conditional statements, but there is no pre-defined way to do so automatically, based on the dynamic simulation environment. Therefore, the proposed CARLA+ takes these different disconnected components of CARLA and provides a unified framework to automate their behaviors leveraging PGMs. For example, a user can define a PGM that models the dynamics of pedestrian counts, vehicle counts, and vehicle speed based on dynamic weather and time of day. CARLA+ is flexible enough and lets the user define the PGM model in different ways: (i) manually defined by the user; (ii) trained on real-world data improving the ability to model different dynamics from the real world. Therefore, instead of manually catering to each condition, CARLA+ enables the user to automate the modeling of different dynamics of the environment. It gives the user more flexibility and control over the dynamic environment, encouraging them to design more complex experimental scenarios.

5. Validation of the Proposed CARLA+

This section carefully discusses the experimental design, implementation details, and the experiments performed in different settings to validate the proposed CARLA+ extension.

5.1. Experimental Setup

In this section, we discuss the experimental setup of the proposed CARLA+ in detail. To validate the proposed CARLA+ solution, all the experiments are conducted in CARLA Town10 map. The motivation behind choosing Town10 is a complex urban setting with detailed high-quality realistic textures and a city comprised of streets, avenues, and pedestrian walkways with various environments. The map layout and the illustration of the simulation environment are shown in Figure 6. Furthermore, the details of different hardware, software, and libraries used to design and develop the CARLA+ are listed in 

Table 3. Hardware and Software Requirements for Experimental Setup.

Requirement	Version	Usage
Operating Sysyem	Windows 11	-
RAM	16 GB	-
CPU	Intel i7	-
GPU	NVIDIA GTX 1080	-
CARLA	v0.9.13	To simulate the environment
Python	v3.7	Scripting language
Pgmpy	v0.1.19	For Bayesian networks
Hydra	v1.2.0	For configuration management
Scikit-learn	v1.0.2	For data analysis
Matplotlib	v3.6.2	For plotting

.

5.2. Experiments

As discussed in Section 4.3 the proposed CARLA+ is designed and developed to be used in different ways to model the dynamics in the environment. Therefore, to validate the proposed extension, we perform two different types of experiments.

5.2.1. Controlled Settings

This experiment aims to model the dynamics between rain, the number of vehicles, and their dynamic speed in the environment. More specifically, a model is developed that can dynamically change the traffic count and speed of the vehicles based on the presence of rain in the environment. Our assumption is that when it is raining, the vehicle count and speed of vehicles will be low, and when it is not raining, it will be high.

Therefore, for this setting, a relatively simple PGM model is designed to validate the effect of rain on the dynamic traffic count and vehicle speed. Three random variables are selected, namely, Rain, Traffic and Speed, having the possible states as shown in

Table 4. Random variables and their states.

Random Variable	States
Rain	NO_RAIN	RAIN
Traffic	LOW	HEAVY
Speed	LOW	HIGH

. The Traffic and Speed variables have a dependency on Rain, and their CPDs are defined manually, as shown in Figure 7.

Firstly, the environment manager reads the weather configuration files and updates the simulation weather accordingly. Then, based on the amount of rain in the simulation environment, the PGM model predicts the state of Traffic and Speed. Finally, a Poisson distribution is used to randomize the actual number of vehicles to spawn and the speed of those vehicles. The value from the predicted state is passed onto the Poisson function as the expected number of events occurring in a fixed time interval, which would return a sample from the parameterized Poisson distribution.

The notion of LOW and HEAVY can be set by the user in the configuration files as well. For example, in one simulation, 20 vehicles might be considered LOW Traffic while in another, it is HEAVY Traffic. These values vary based on the dynamic simulation environment and experiment settings and can be configured easily via configuration files.

This minimal and bare-bones experiment aims to showcase the effectiveness and usefulness of CARLA+ even in the simplest of scenarios. Simple rules and dependencies are used to model the dynamic environment, which would then generate values from random distributions to better model the randomness inherent in the real world. Given that we use a Poisson distribution to select the actual value, instead of a hard-coded one, we ran the experiment 1200 times for each of the scenarios, i.e., NO_RAIN and RAIN to better showcase the effectiveness of this approach. As can be seen in Figure 8, the resulting graph shows that in the case of NO_RAIN, the Speed and Traffic is low, while in the case of RAIN, their values are generally high. This shows that even such simple rules and models can be used to create dynamic environments easily using the proposed CARLA+.

5.2.2. Learning-Based Settings

For this experiment, the objective is to showcase the utility of CARLA+ when modeling the simulation environment based on dynamics learned from real-world data. For this purpose, different features are collected from the real world and a BN is trained based on that data. The trained network is then exploited in the CARLA+ framework to simulate the dynamic environment of the real world.

To validate the full potential of the CARLA+, in this experiment we used real-world data to model the simulation environment. Weather and traffic data from different sources are collected, and the relevant features are extracted to train a PGM model that reflects real-world dynamics more acutely, as compared to hand-crafted CPDs. This section provides a detailed discussion of all the steps involved in learning a PGM model as shown in Figure 9 and the results achieved in this setting.

In what follows next, we discuss each step in detail.

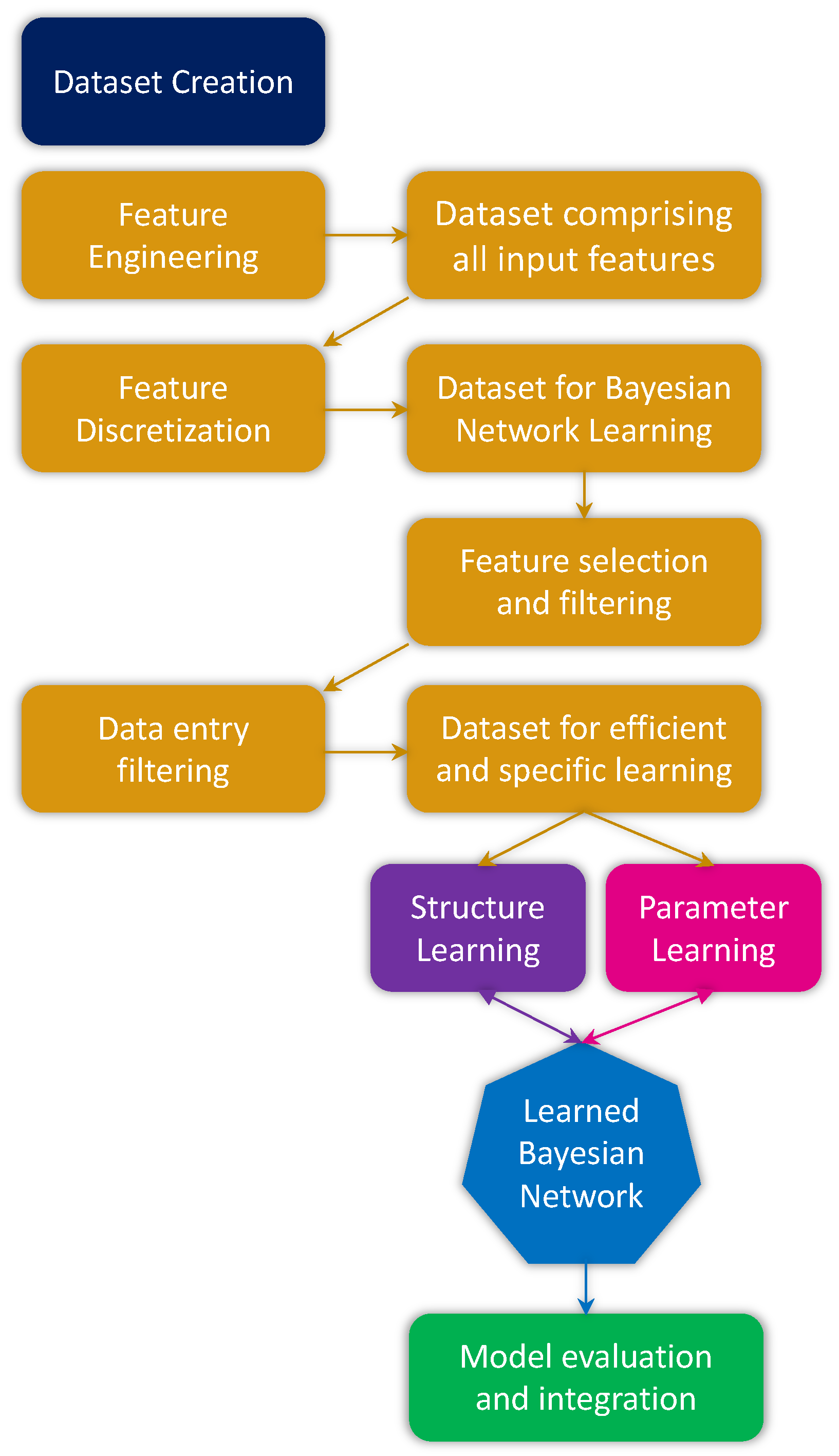
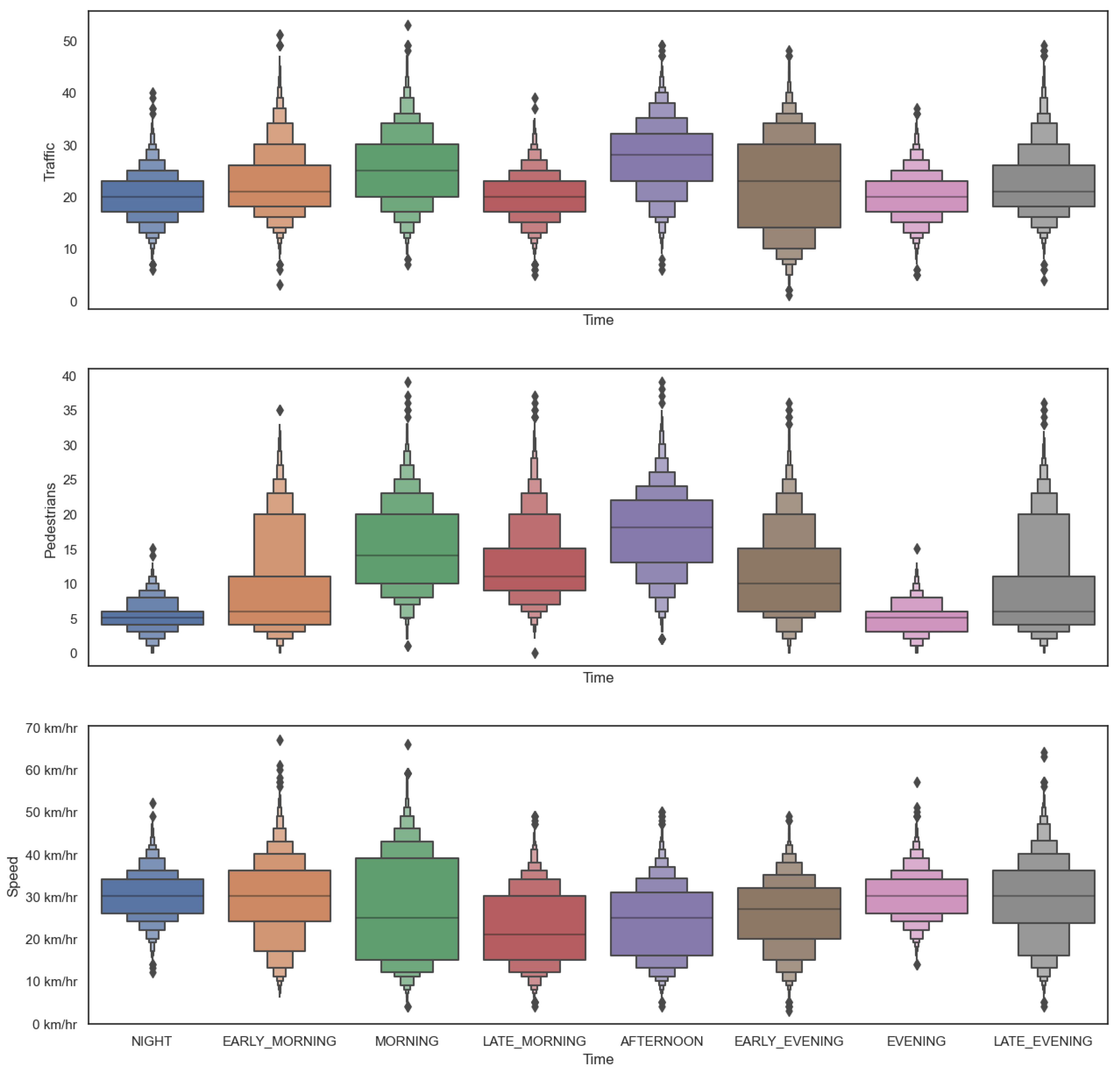
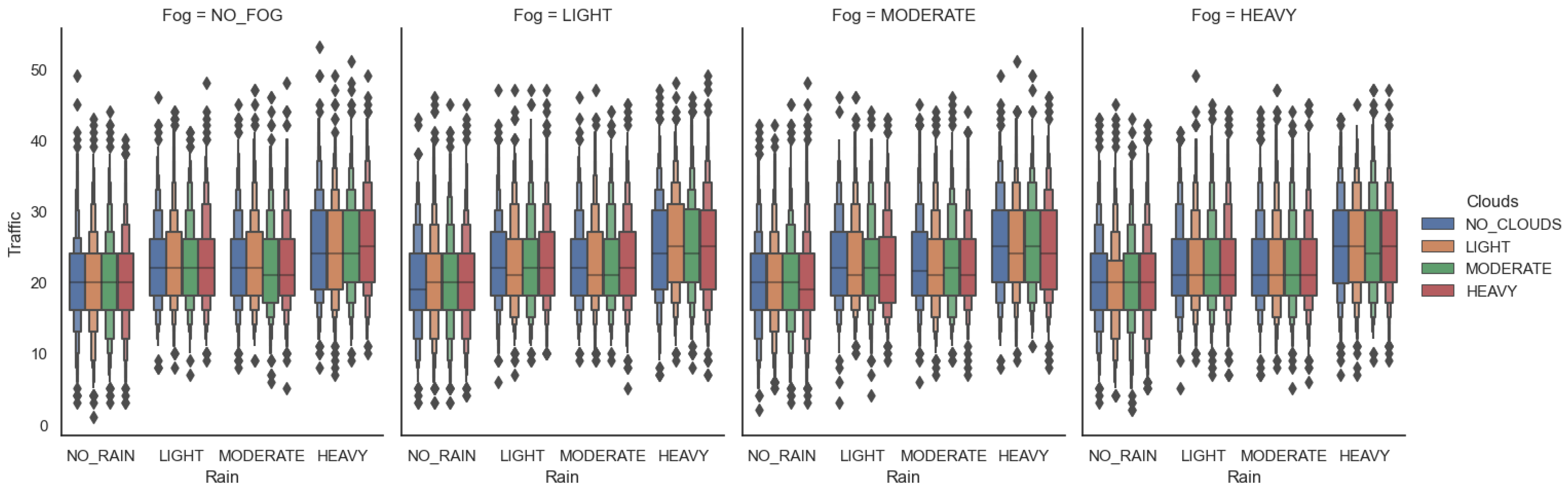
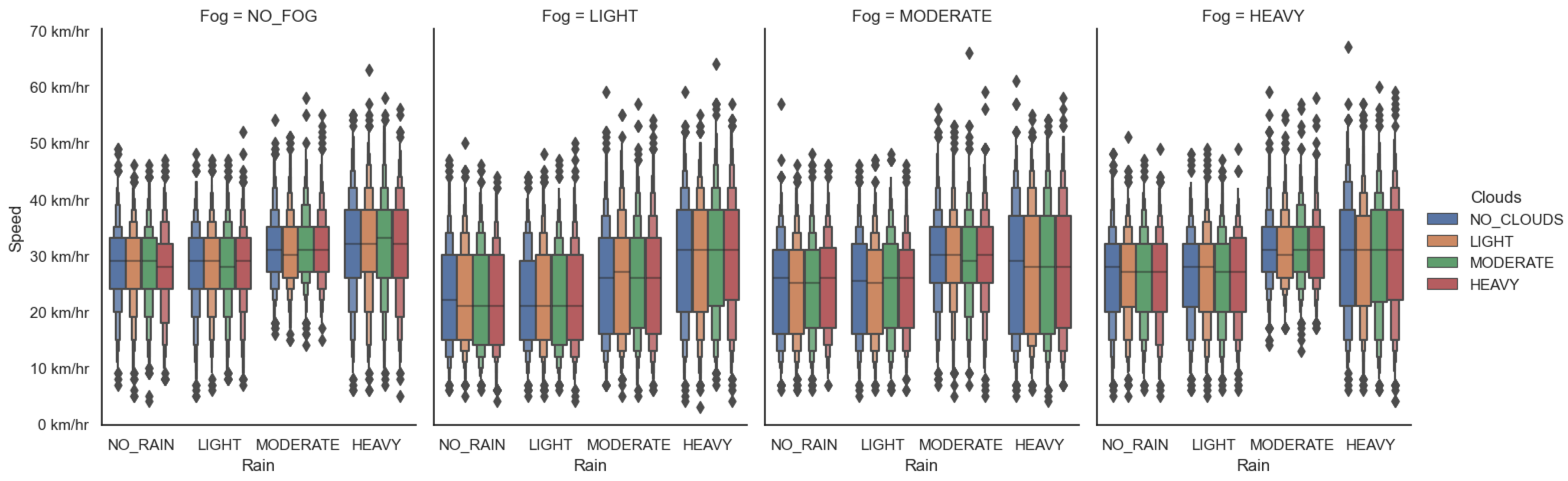
Dataset Creation

For this experiment, we aim to model the effect of weather and time of day on traffic count, pedestrian counts, and vehicle speed in a dynamic environment. After a thorough search, we did not find any relevant dataset which contained data about traffic count, traffic speed, pedestrian count, and weather. Therefore, we created such a dataset ourselves and selected the dataset for New York City, as it satisfied all of our data requirements. The detail of all the data sources that we used to create the new dataset are discussed below:

• Traffic Count: for the traffic count, we used New York City’s open data platform [20] which contains data for traffic volume counts. It contains traffic volume data of different streets in the boroughs of New York City, taken at 15-minute intervals.
• Pedestrian Count: for pedestrians counts, we used the Brooklyn Bridge Automated Pedestrian Counts data [21], which contains pedestrian count as well as basic weather data, taken at 1-hour intervals.
• Traffic Speed: we used New York City’s Real-Time Traffic Speed data [22] which is comprised of the traffic speed as well as the borough where the data were captured.
• Weather: the NYC weather data are taken from Open-Meteo’s Historical Weather API [23] for the city of Brooklyn.

We selected the data from the year 2019 as they contained the largest number of entries in all the datasets, and created a unified dataset containing 8670 rows corresponding to every hour in the year 2019. Our new dataset is openly available for researchers at  https://www.kaggle.com/datasets/aadimator/brooklyn-2019-traffic-data (accessed on 2 January 2023) to experiment and validate their solutions.

Data Preparation and Feature Engineering

Once we have data corresponding to every hour in the year 2019, we filtered it to only contain the data for Brooklyn City, as the pedestrian count only corresponds to that. To handle the missing entries, we employed the backward fill method, where the null entry is replaced with the previous entry. For this experiment, we aim to validate the effect of weather and time of day on traffic and pedestrian counts, as well as their effect on traffic speed. Thus, we filtered only the relevant columns from the dataset, resulting in the following final columns:

• Hour
• Pedestrians
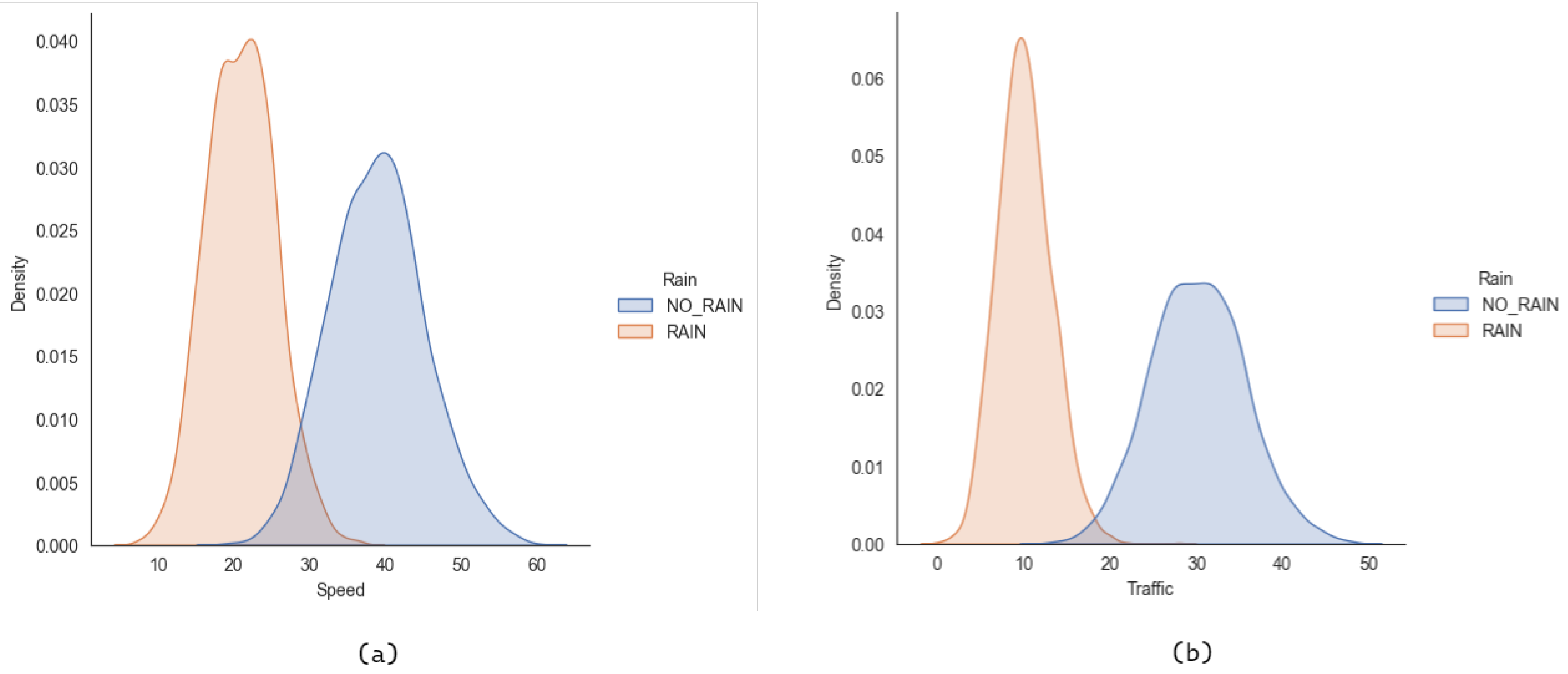
• Traffic
• Speed
• Rain
• Fog
• Clouds

As most of these columns contain continuous values, we further discretize them to be used in a BN. The variable Hour is classified into the time of days, as shown in

Table 5. Hour classification into the time of the day.

Hour Classification into Time of the Day
2:00 AM to 6:00 AM	Early Morning
6:00 AM to 9:00 AM	Morning
9:00 AM to 12:00	Late Morning
12:00 PM to 5:00 PM	Afternoon
5:00 PM to 7:00 PM	Eary Evening
7:00 PM to 9:00 PM	Evening
9:00 PM to 11:00 PM	Late Evening
11:00 PM to 2:00 AM	Night

. Moreover, the Rain, Fog, and Clouds variables are discretized into four categories based on the rules defined in

Table 6. Rules to discretize the Rain, Fog, and Clouds parameters.

Label	Rain (mm/h)	Fog (%)	Clouds (%)
NO	0	0–25	0–25
LIGHT	0.1–2.5	25–50	25–50
MODERATE	2.6–7.5	50–75	50–75
HEAVY	>7.5	75–100	75–100

. As for the discretization of Traffic, Pedestrians, and Speed parameters, they are divided into three bins based on their data distributions, as shown in

Table 7. Rules to discretize the Traffic, Pedestrian, and Speed parameters.

Label	Traffic	Pedestrian	Speed (km/h)
LOW	0–200	0–100	0–30
MEDIUM	200–800	100–1200	30–45
HIGH	>800	>1200	45–55

. The final processed and discretized dataset is made publicly available at the following link https://www.kaggle.com/datasets/aadimator/brooklyn-2019-traffic-data (accessed on 2 January 2023).

Learning and Integration of PGM Model

Once the data have been cleaned, pre-processed and discretized, we learn the BN based on two stages: (i) structure learning and (ii) parameter learning.

Structure learning is used to learn the network structure of the BN and to highlight the dependencies of different variables on one another. For this purpose, the HC algorithm is used, and the best-scoring network structure is selected, as shown in Figure 10. The BN structure depicted in Figure 10 shows that only two of the seven random variables, Time and Clouds, are independent, while all the rest are dependent on one or another.

After learning the structure of the BN, the Bayesian estimator algorithm is used for parameter learning. It learns the CPDs for different variables directly from the dataset that we created previously. Some of the parameters used to learn the structure and parameter learning are presented in

Table 8. Parameters for structure and parameter learning.

Learning Stage	Parameter	Value
Structure Learning	Scoring method	k2score
	Epsilon	1 × 10${}^{-6}$
	White list	Possible edges
Parameter Learning	Estimator	BayesianEstimator
	Prior type	BDeu
	Equivalent sample size	10
	Complete samples only	FALSE

. Once trained, the model is evaluated based on certain criteria and then integrated into our CARLA+ by updating the random variables and their states in the model and variable configuration files. This trained model is then used to model the dynamics of the real world in the simulated environment which allows us to design customized dynamic and more realistic scenarios.

The model is used to infer the state of a certain variable given the states of others, and a Poisson distribution is then used to sample actual values based on the inferred state. Due to the inherent randomness incurred by the utilization of Poisson distribution, we collected 100 samples relating to each permutation of the different variable states, giving us a total of 51,200 data samples. These samples are then used to visualize and present the results of the trained model. The experimental results show the distribution of Speed, Pedestrian, and Traffic variables with respect to Time of the day in Figure 11. In Figure 11, the different states of Time are represented along the x-axis, and the $y-$axis corresponds to the values from the three different modalities, which are Traffic, Pedestrians, and Speed. The graph in Figure 11 shows the distributions of values we get from the Poisson distribution in each particular time state. Figure 12, Figure 13 and Figure 14 show the distributions of traffic, speed, and pedestrians, respectively. The distribution for each variable is represented with respect to the different states of Rain, Fog, and Clouds. In Figure 12, Figure 13 and Figure 14, the $x-$axis and the color correspond to the states of Rain and Clouds, respectively, while the columns represent different states of Fog. Moreover, some of the results of the simulation environment are shown in Figure 15, Figure 16 and Figure 17. All of these distributions are localized to Brooklyn City, and the year 2019. Different cities and time intervals would result in different traffic scenarios and behaviors, and as a result, different resulting distributions.

From these experimental results, we have demonstrated that CARLA+ has the potential to model the dynamics of real-world scenarios more effectively and efficiently. Instead of hand-crafted rules to model certain requirements, CARLA+ can be used to automatically handle the scenarios based on their defined CPDs, which can be either hand-crafted or trained via machine learning algorithms.

6. Conclusions

Autonomous driving in an uncontrolled urban environment is challenging due to the environment dynamics, weather types, heterogeneous vehicles, pedestrians, etc. Therefore, an obvious challenge in this regard is to correctly model the environment that captures the dynamics of this problem domain. To cope with this challenge, the proposed research models the dynamics of the environment leveraging the probabilistic graphical model. The motivation behind using PGM is that it is a robust framework for encoding probability distributions for this complex domain by computing the joint distributions over numerous random variables that interact with one another. Therefore, to develop the proposed solution, we rely on the classical CARLA simulator. It provides rich features; however, it still fails on a few fronts, therefore, there is a dire need to extend the off-the-shelf CARLA with more sophisticated settings that can model the required dynamics. To this end, we have thoroughly designed and developed CARLA+, an extension of classical CARLA. The CARLA+ based on the PGM framework is capable enough to model the dynamics of the environment such as time of the day and weather types, predict the vehicle count in the environment, and predict the speed of the vehicles based on the weather, and predict the number of pedestrians with respect to time and weather, etc. Experiments with different controlled and learning-based settings have been conducted, ranging from hand-crafted PGMs to complex PGMs learned directly from real-world data. The experimental results demonstrated that CARLA+ is flexible enough to be used in various ways to model the dynamics of the environment. In the future, we plan to extend CARLA+ by allowing for more configurable parameters and more flexibility on the type of probabilistic networks and models one can choose.