A Novel Semidefinite Programming-based UAV 3D Localization Algorithm with Gray Wolf Optimization
Abstract
:1. Introduction
- A system model for the design and analysis of 3D UAV localization is developed. We consider distance measurement-based UAV position estimation as an objective optimization problem with quadratic constraints and formulate it as a maximum likelihood estimation (MLE) problem. A localization model for the design of UAVs in a 3D moving scene is developed. We consider the distance-based UAV position estimation as an objective optimization problem with quadratic constraints and formulate it as an MLE problem.
- The SDP and RLT relaxation constraints are established based on the distance constraints of the localization problem, and the solvability and tightness of the proposed composite algorithm SDP + RLT are analyzed.
- In addition, our solution is extended to the case of noisy distance measurement errors and loss, and an I-GWO algorithm is proposed, which greatly improves localization accuracy. Finally, we validate the excellence of the proposed scheme by comparing multiple sets of experimental results.
2. Related Works
3. Problem Formulation
4. Proposed Localization Solution
4.1. System Model
4.1.1. SDP Solvability Analysis
4.1.2. Unique Solvability Analysis
4.2. SDP Plus RLT Relaxation Scheme
The Tightness Analysis
| Algorithm 1 SDP + RLT Method for UAV Localization |
| Input: ak, m, n, , , k,j, di,j, R, l, u, ϵ. Output: positions of unknown UAV nodes x1, x2, …, xn. 1: begin /*Initialization*/ 2: Initialize the Euclidean distance matrix Z = [I3, X; XT,Y], where Y = XTX. 3: Z = Symmetrize (Z) 4: cvx begin 5: minimize norm(X, 2) 6: s.t. 7: for each UAV i ← 1 to n do 8: update Z by solving Problem (14). 9: end for 10: if Z ≤ 0 then 11: break; 12: end if 13: cvx end 14: end |
5. Bionic Optimization Algorithm
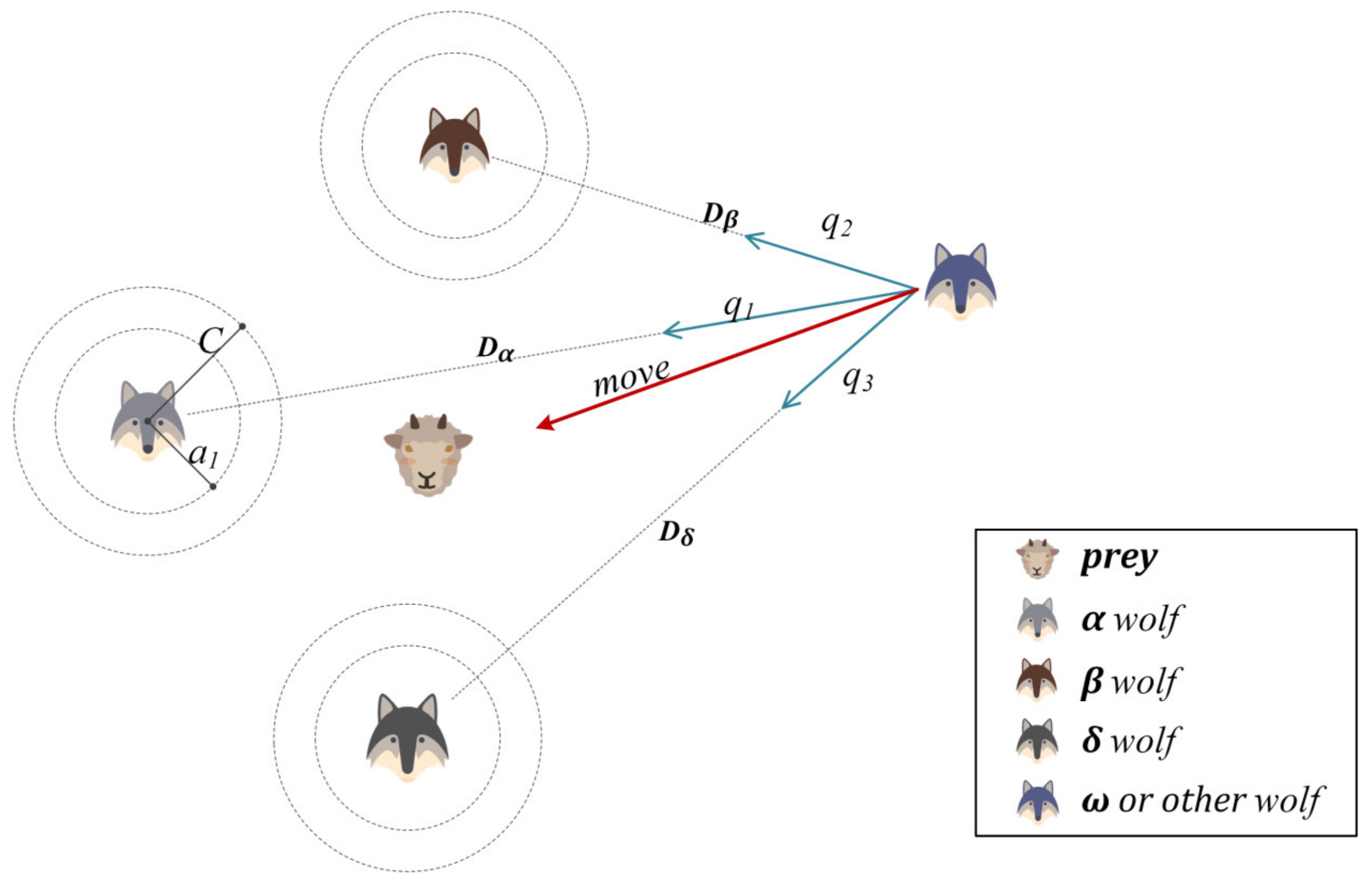
5.1. Motivation
5.2. I-GWO Algorithm
| Algorithm 2 I-GWO of UAV Localization Optimization |
| Input: Preliminary results Xi of SDP + RLT, population size U, max iterations tmax, dimension d, and coefficients r1, r2, q1, q2, and q3. Output: Optimal position of the unknown UAVs. /*Initialization*/ 1: Initialize the gray wolf pack using Xi. 2: Initialize the GWO parameters (a, A, C). 3: Initialize the fitness value (Uα, Uβ, Uδ). /*Computation*/ 4: while (t ≤ tmax) do 5: for each wolf w = 1: W do 6: Update the current search agent position using (18) 7: end for /*I-GWO loop*/ 8: for each wolf w = 1: W do 9: Evaluate the fitness value and update (Uα, Uβ, Uδ) 10: Obtain the variable a based on (23). 11: end for 12: for each wolf w = 1: W do 13: Calculate A and C based on (19) 14: Update the position of wolf w by (24)(25) 15: end for 16: w = w + 1 17: t = t + 1 18: end while 19: Terminate the process and output the optimal position by Uα 20: end |
6. Simulation
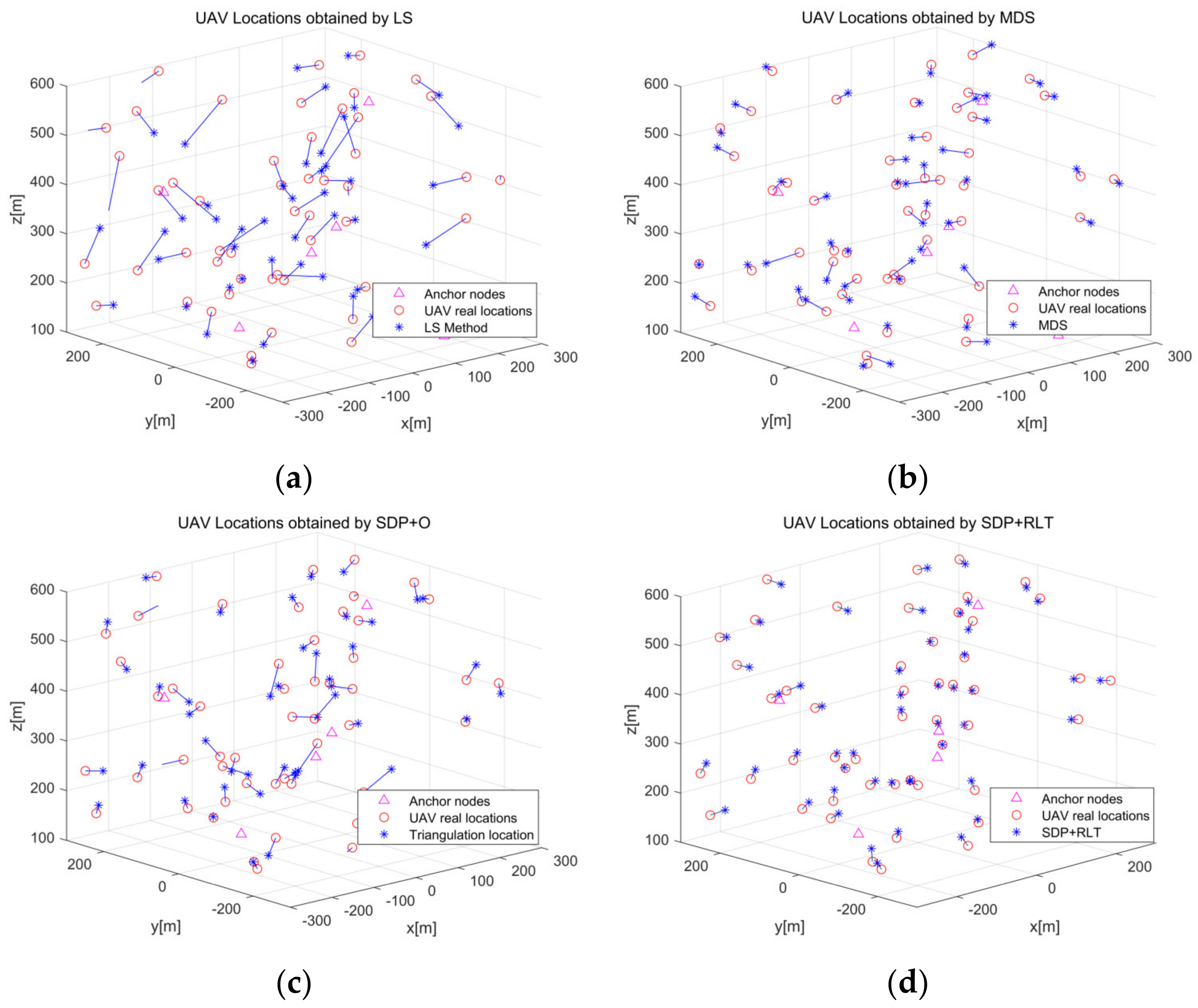
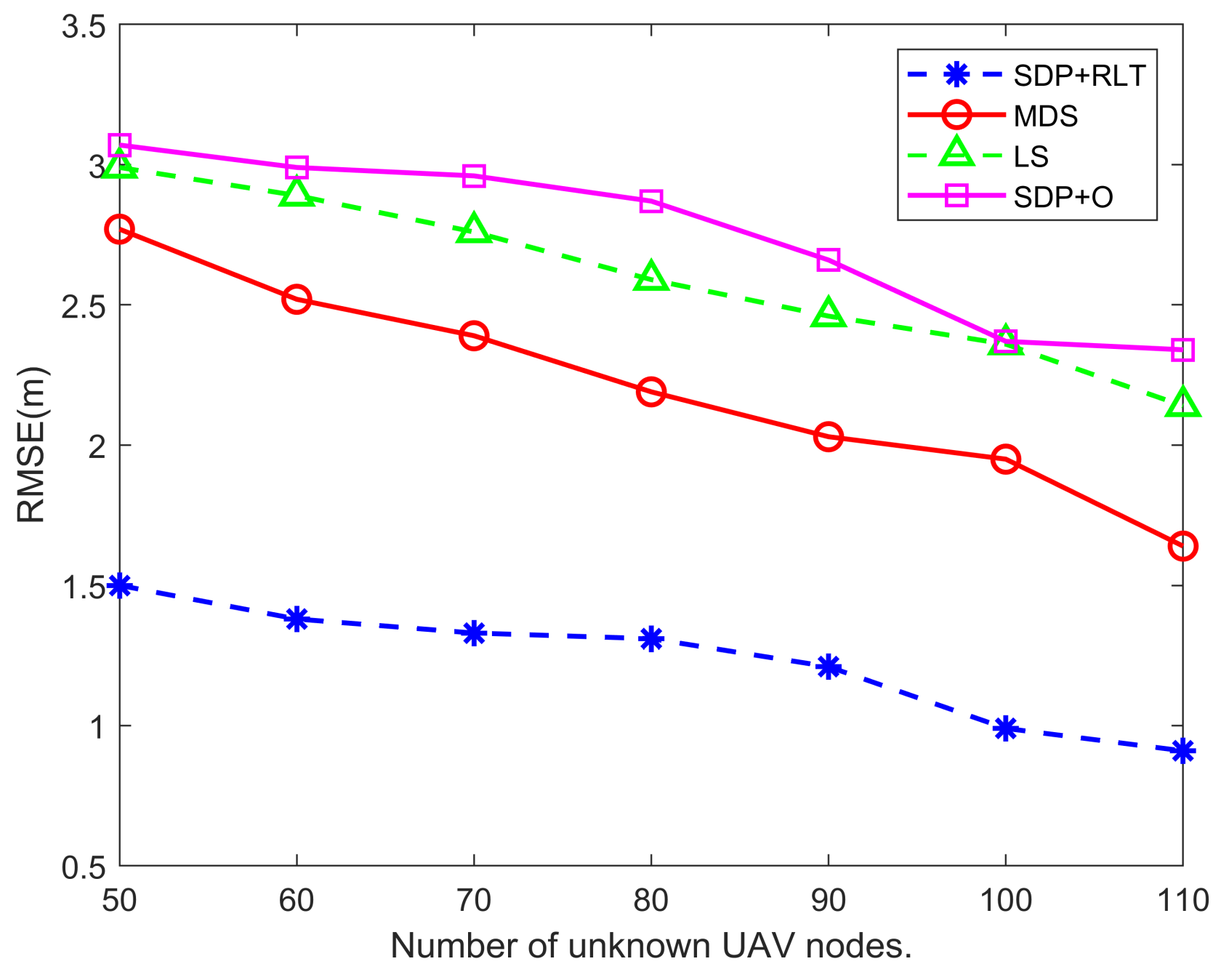
6.1. Performance of Proposed Method
6.2. Simulation Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ashish, S.; Prakash, J. Future FANET with application and enabling techniques: Anatomization and sustainability issues. Comput. Sci. Rev. 2021, 39, 100359. [Google Scholar]
- Tang, F.; Kawamoto, Y.; Kato, N.; Liu, J. Future intelligent and secure vehicular network toward 6G: Machine-learning approaches. Proc. IEEE 2020, 108, 292–307. [Google Scholar] [CrossRef]
- Orfanus, D.; De Freitas, E.; Eliassen, F. Self-Organization as a Supporting Paradigm for Military UAV Relay Networks. IEEE Commun. Lett. 2016, 20, 804–807. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Unmanned Aerial Vehicle with under Laid Device-to-Device Communications: Performance and Tradeoffs. IEEE Trans. Wirel. Commun. 2016, 15, 3949–3963. [Google Scholar]
- Guo, K.; Li, X.; Xie, L. Simultaneous cooperative relative localization and distributed formation control for multiple UAVs. Sci. China Inf. Sci. 2020, 63, 119201. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, J.; Wang, W.-Q.; Yang, H. Classification and localization of mixed near-field and far-field sources using mixed-order statistics. Signal Process. 2018, 143, 134–139. [Google Scholar] [CrossRef]
- Li, W.; Jelfs, B.; Kealy, A.; Wang, X.; Moran, B. Cooperative Localization Using Distance Measurements for Mobile Nodes. Sensors 2021, 21, 1507. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Z.; Wang, Y.; Wang, Z.; Yu, L. Three passive TDOA-AOA receivers-based flying-UAV positioning in extreme environments. IEEE Sens. J. 2020, 20, 9589–9595. [Google Scholar] [CrossRef]
- Kang, Y.; Wang, Q.; Wang, J.; Chen, R. A high-accuracy TOA-based localization method without time synchronization in a three-dimensional space. IEEE Trans. Ind. Inform. 2018, 15, 173–182. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Russell, J.S.; Ye, M.; Anderson, B.D.O.; Hmam, H.; Sarunic, P. Cooperative localization of a GPS-denied UAV using direction-of-arrival measurements. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1966–1978. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. Localization and clustering based on swarm intelligence in UAV networks for emergency communications. IEEE Internet Things J. 2019, 6, 8958–8976. [Google Scholar] [CrossRef]
- Yeasir, A.M.; Moh, S. Bio-inspired approaches for energy-efficient localization and clustering in UAV networks for monitoring wildfires in remote areas. IEEE Access 2021, 9, 18649–18669. [Google Scholar]
- Biswas, P.; Liang, T.-C.; Toh, K.-C.; Ye, Y.; Wang, T.C. Semidefinite programming approaches for sensor network localization with noisy distance measurements. IEEE Trans. Autom. Sci. Eng. 2006, 3, 360–371. [Google Scholar] [CrossRef]
- Guo, K.; Li, X.; Xie, L. Ultra-wideband and odometry-based cooperative relative localization with application to multi-uav formation control. IEEE Trans. Cybern. 2019, 50, 2590–2603. [Google Scholar] [CrossRef] [PubMed]
- Baldi, S.; Roy, S.; Yang, K. Towards adaptive autopilots for fixed-wing unmanned aerial vehicles. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020; pp. 4724–4729. [Google Scholar] [CrossRef]
- Wang, X.; Roy, S.; Farì, S.; Baldi, S. Adaptive Vector Field Guidance Without a Priori Knowledge of Course Dynamics and Wind. IEEE/ASME Trans. Mechatron. 2022, 27, 4597–4607. [Google Scholar] [CrossRef]
- Shang, Y.; Ruml, W. Improved MDS-based localization. In Proceedings of the IEEE INFOCOM 2004, Hong Kong, China, 7–11 March 2004; Volume 4, pp. 2640–2651. [Google Scholar]
- Wan, C.; You, S.; Jing, G.; Dai, R. A distributed algorithm for sensor network localization with limited measurements of relative distance. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 4677–4682. [Google Scholar]
- Zhang, Y.; Chen, Y.; Liu, Y. Towards unique and anchor-free localization for wireless sensor networks. Wirel. Pers. Commun. 2012, 63, 261–278. [Google Scholar] [CrossRef]
- Parulpreet, S.; Khosla, A.; Kumar, A.; Khosla, M. Optimized localization of target nodes using single mobile anchor node in wireless sensor network. AEU-Int. J. Electron. Commun. 2018, 91, 55–65. [Google Scholar]
- Liu, Y.; Wang, Y.; Wang, J.; Shen, Y. Distributed 3D relative localization of UAVs. IEEE Trans. Veh. Technol. 2020, 69, 11756–11770. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Y.; Liu, W.; Wang, L. PMDV-hop: An effective range-free 3D localization scheme based on the particle swarm optimization in wireless sensor network. KSII Trans. Internet Inf. Syst. (TIIS) 2018, 12, 61–80. [Google Scholar]
- Nguyen, T.V.; Jeong, Y.; Shin, H.; Win, M.Z. Least square cooperative localization. IEEE Trans. Veh. Technol. 2015, 64, 1318–1330. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Ansari, N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements. IEEE Trans. Veh. Technol. 2013, 62, 853–862. [Google Scholar] [CrossRef]
- Shang, Y.; Ruml, W.; Zhang, Y.; Fromherz, M. Localization from connectivity in sensor networks. IEEE Trans. Parallel Distrib. Syst. 2004, 15, 961–974. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, H.; Wan, Q. An Iterative Method for Moving Target Localization Using TDOA and FDOA Measurements. IEEE Access 2018, 6, 2746–2754. [Google Scholar] [CrossRef]
- Calafiore Giuseppe, C.; Carlone, L.; Wei, M. A distributed technique for localization of agent formations from relative range measurements. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2012, 42, 1065–1076. [Google Scholar] [CrossRef]
- Pratik, B.; Lian, T.-C.; Wang, T.; Ye, Y. Semidefinite programming based algorithms for sensor network localization. ACM Trans. Sens. Netw. (TOSN) 2006, 2, 188–220. [Google Scholar]
- Man-Cho, A.; Ye, Y. Theory of semidefinite programming for sensor network localization. Math. Program. 2007, 109, 367–384. [Google Scholar]
- Anstreicher, K.M. Semidefinite programming versus the reformulation-linearization technique for nonconvex quadratically constrained quadratic programming. J. Glob. Optim. 2009, 43, 471–484. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, H.; Wang, W.; So, H.C. Source localization using TDOA and FDOA measurements based on semidefinite programming and reformulation linearization. J. Frankl. Inst. 2019, 356, 11817–11838. [Google Scholar] [CrossRef]
- Raguraman, P.; Ramasundaram, M.; Balakrishnan, V. Localization in wireless sensor networks: A dimension based pruning approach in 3D environments. Appl. Soft Comput. 2018, 68, 219–232. [Google Scholar] [CrossRef]



| Symbol | Definition |
|---|---|
| Na, Nu, NR | Set of anchors and target UAVs, where NR = Na + Nu |
rij, αij, sj, nij X, Y, Z | Coordinate of the anchor UAVs and target UAVs Distance between target UAV and UAV (or anchor) Set of distance pairs of UAV/UAV and UAV/anchor Amplitude, waveform, and noise of UAV signal Gaussian noise of distance measurements X is UAV position matrix and Y = XTX, Z = [I3 X; XT Y] |
| l, u U a, r1, r2 | Lower and upper bounds of variables in X Variables greater than 1 and less than e Population of gray wolves Convergence factor and two random numbers of [0,1] |
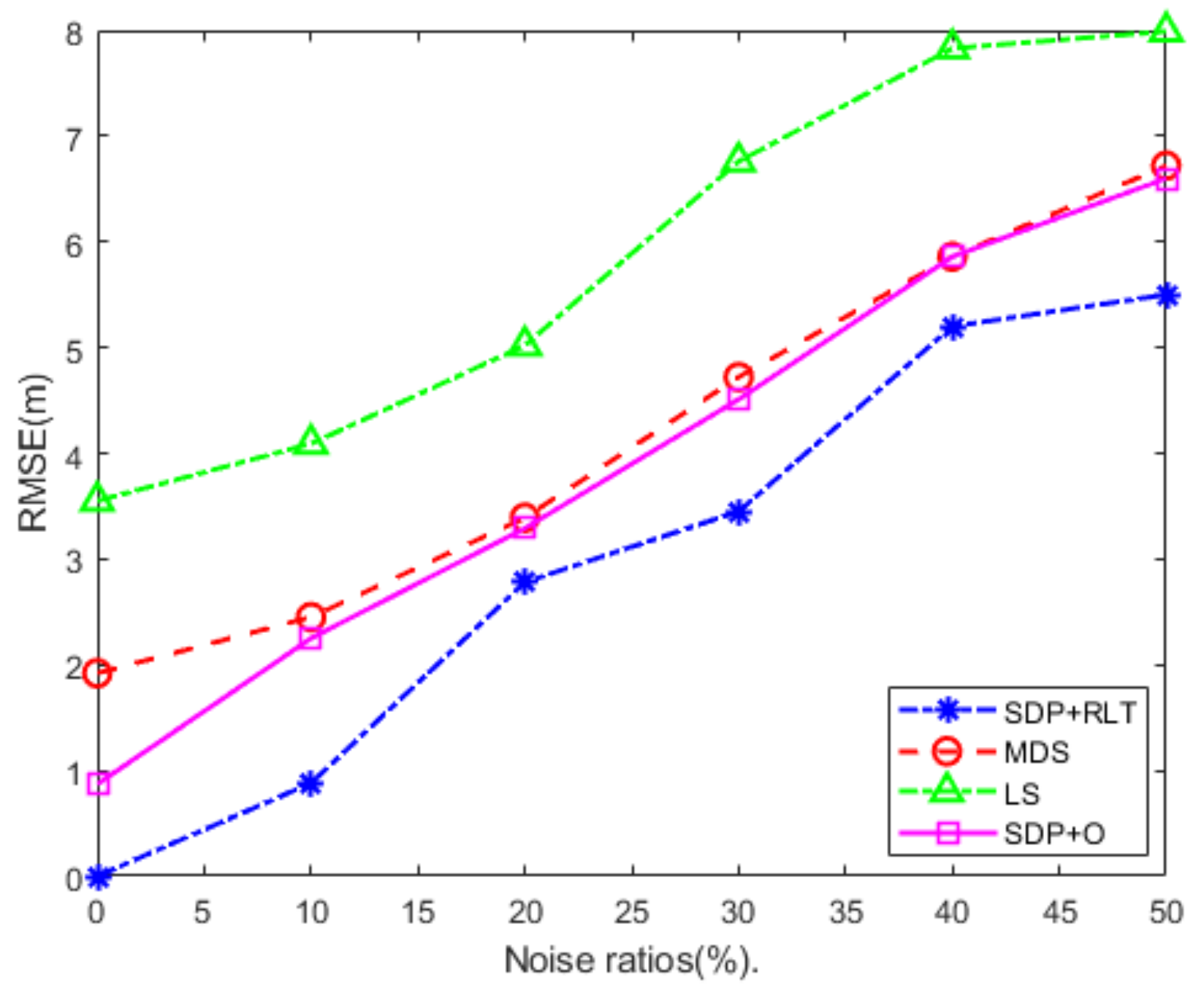
| Localization Algorithm/RMSE | Numbers of Unknown UAV Nodes | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 60 | 70 | 80 | 90 | 100 | 110 | |
| LS | 2.9912 | 2.8923 | 2.7633 | 2.5908 | 2.4648 | 2.3567 | 2.1435 |
| MDS | 2.7732 | 2.5243 | 2.3957 | 2.1894 | 2.0362 | 1.9533 | 1.6415 |
| SDP + O | 3.0796 | 2.9923 | 2.9617 | 2.8796 | 2.6695 | 2.3709 | 2.3474 |
| SDP + RLT | 1.5057 | 1.3809 | 1.3385 | 1.3196 | 1.2061 | 0.9921 | 0.9107 |
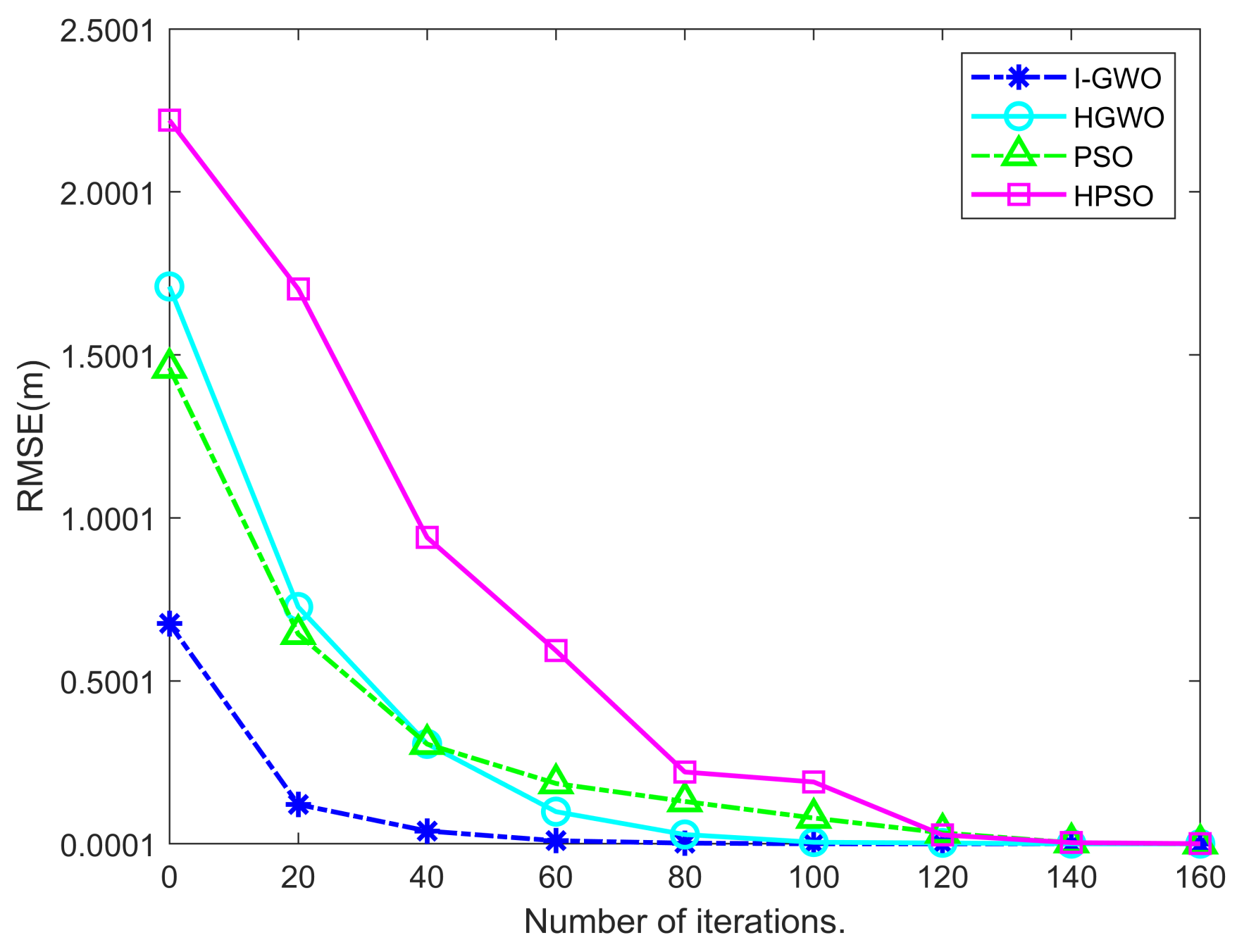
| Optimization Algorithm/RMSE | Iterations | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | |
| PSO | 1.4602 | 0.6434 | 0.3061 | 0.1853 | 0.1302 | 0.0794 | 0.0337 | 0.0036 | 0.0015 |
| HPSO | 1.7132 | 0.7266 | 0.3068 | 0.0988 | 0.0287 | 0.005 | 0.0027 | 5.56 × 10−5 | 7.35 × 10−7 |
| HGWO | 2.2296 | 1.7022 | 0.9412 | 0.5926 | 0.2205 | 0.1899 | 0.0274 | 0.0038 | 0.0006 |
| I-GWO | 0.6757 | 0.1209 | 0.0395 | 0.0096 | 0.0061 | 0.0021 | 3.21 × 10−6 | 2.57 × 10−8 | 1.82 × 10−11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Xia, X.; Yan, Y. A Novel Semidefinite Programming-based UAV 3D Localization Algorithm with Gray Wolf Optimization. Drones 2023, 7, 113. https://doi.org/10.3390/drones7020113
Li Z, Xia X, Yan Y. A Novel Semidefinite Programming-based UAV 3D Localization Algorithm with Gray Wolf Optimization. Drones. 2023; 7(2):113. https://doi.org/10.3390/drones7020113
Chicago/Turabian StyleLi, Zhijia, Xuewen Xia, and Yonghang Yan. 2023. "A Novel Semidefinite Programming-based UAV 3D Localization Algorithm with Gray Wolf Optimization" Drones 7, no. 2: 113. https://doi.org/10.3390/drones7020113
APA StyleLi, Z., Xia, X., & Yan, Y. (2023). A Novel Semidefinite Programming-based UAV 3D Localization Algorithm with Gray Wolf Optimization. Drones, 7(2), 113. https://doi.org/10.3390/drones7020113






