Low-Complexity Three-Dimensional AOA-Cross Geometric Center Localization Methods via Multi-UAV Network
Abstract
:1. Introduction
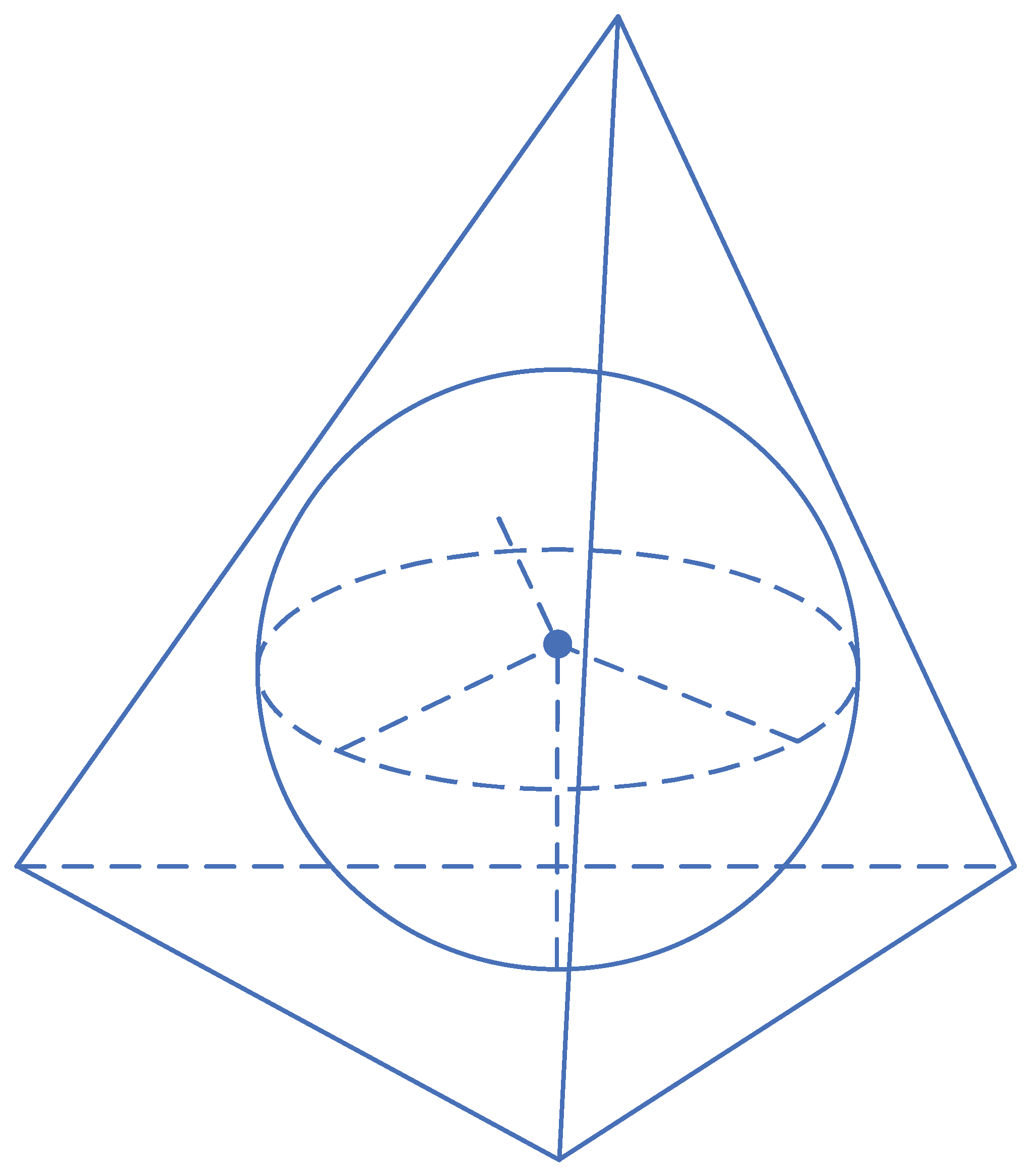
- Three-dimensional AOA positioning is considered in this paper. Inspired by the inscribed sphere of a tetrahedron, we extend every angle to a plane. Then, the 3-D AOA localization can be used to seek out the centers of inscribed spheres for these multiple planes. Our method can not only accurately estimate the source position and the noise level at the same time, but it also has very low computational complexity, which is similar to the conventional least square (LS) estimator.
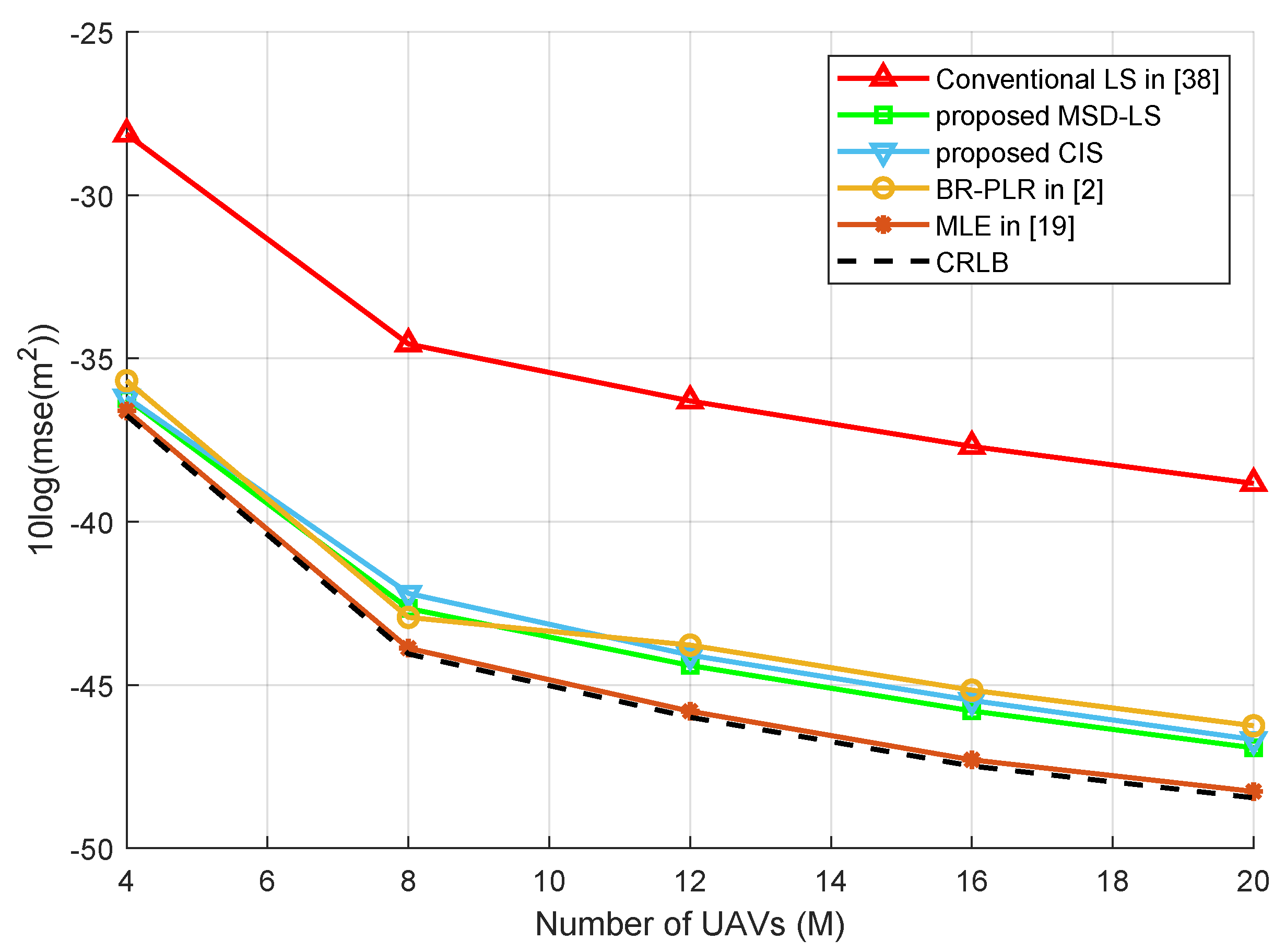
- To further reduce computational complexity, the estimation for variance of angle noise is removed. Then, the second algorithm is born. This algorithm is based on the sum of the minimum squared distance from the estimated point to all planes. The original optimization problem can be converted to a LS problem. Thus, this method has lower computational complexity due to its closed-formed solution. The simulation results show that these two methods have similar performance. Furthermore, compared with conventional LS, the proposed methods have about 8 dB of gain.
- The CRLB and computational complexity are presented. Theoretical analysis and simulation results respectively unveiled that the performance of the proposed methods is close to CRLB and the computational complexity is reduced significantly. The proposed methods could achieve a satisfactory balance between the performance and computational complexity.
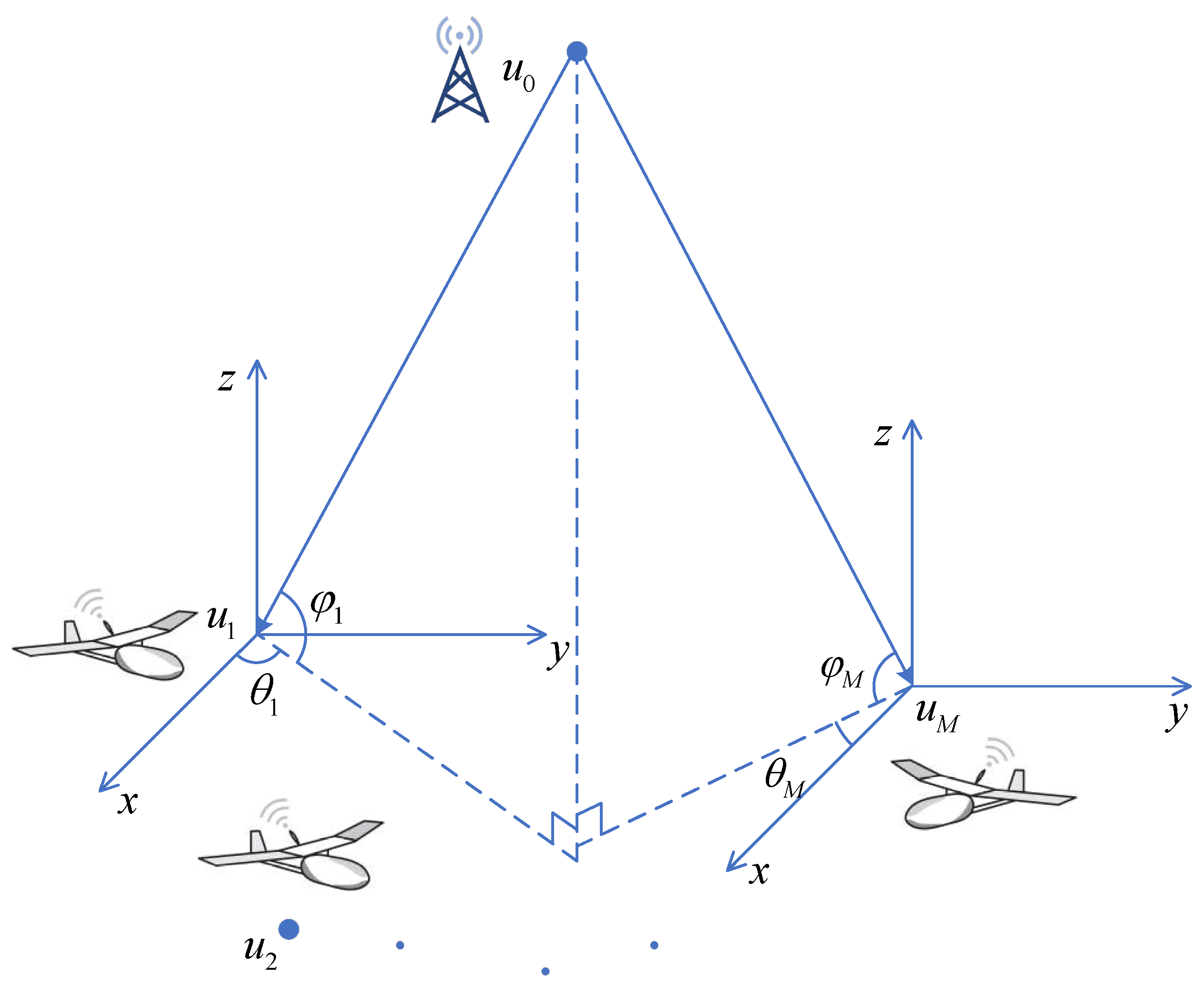
2. System Model
3. Proposed Center of Inscribed Sphere-Based Methods for AOA Localization
3.1. Proposed Center of the Inscribed Sphere Method
3.2. Proposed Minimum Squared Distance Method
4. Analysis
4.1. Performance Accuracy
4.2. Computational Complexity
5. Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3-D | Three-dimensional |
| UAV | Unmanned aerial vehicle |
| MIMO | Multiple-input, multiple-output |
| LOS | Line-of-sight |
| DOA | Directory of arrival |
| RSS | Received signal strength |
| AOA | Angle of arrival |
| TOA | Time od arrival |
| CRLB | Cramér–Rao lower bound |
| WSN | Wireless sensor network |
| MLE | Maximum likelihood estimator |
| IoT | Internet of Things |
| CSI | Channel state information |
| OTFS | Orthogonal time frequency space |
| MUSIC | Multiple signal classification |
| ANM | Atomic norm minimization |
| CIS | Center of the inscribed sphere |
| MSD | Minimum squared distance |
| BR-PLE | Bias reduction pseudolinear estimator |
References
- Wan, P.; Huang, Q.; Lu, G.; Wang, J.; Yan, Q.; Chen, Y. Passive localization of signal source based on UAVs in complex environment. China Commun. 2020, 17, 107–116. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. An Asymptotically Efficient Estimator in Closed-Form for 3-D AOA Localization Using a Sensor Network. IEEE Trans. Wirel. Commun. 2015, 14, 6524–6535. [Google Scholar] [CrossRef]
- Kaur, N.; Sood, S.K. An Energy-Efficient Architecture for the Internet of Things (IoT). IEEE Syst. J. 2017, 11, 796–805. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Liu, F.; Jing, X.; Mu, J. Integrating Sensing and Communications for Ubiquitous IoT: Applications, Trends, and Challenges. IEEE Netw. 2021, 35, 158–167. [Google Scholar] [CrossRef]
- Wu, Z.H.; Han, Y.; Chen, Y.; Liu, K.J.R. A Time-Reversal Paradigm for Indoor Positioning System. IEEE Trans. Veh. Technol. 2015, 64, 1331–1339. [Google Scholar] [CrossRef]
- Le Dortz, N.; Gain, F.; Zetterberg, P. WiFi fingerprint indoor positioning system using probability distribution comparison. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2301–2304. [Google Scholar]
- Ho, K.; Chan, Y. Geolocation of a known altitude object from TDOA and FDOA measurements. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 770–783. [Google Scholar] [CrossRef]
- Ho, K.C.; Lu, X.; Kovavisaruch, L. Source Localization Using TDOA and FDOA Measurements in the Presence of Receiver Location Errors: Analysis and Solution. IEEE Trans. Signal Process. 2007, 55, 684–696. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H. An Importance Sampling Method for TDOA-Based Source Localization. IEEE Trans. Wirel. Commun. 2011, 10, 1560–1568. [Google Scholar] [CrossRef]
- Ho, K.C. Bias Reduction for an Explicit Solution of Source Localization Using TDOA. IEEE Trans. Signal Process. 2012, 60, 2101–2114. [Google Scholar] [CrossRef]
- Meng, W.; Xie, L.; Xiao, W. Optimality Analysis of Sensor-Source Geometries in Heterogeneous Sensor Networks. IEEE Trans. Wirel. Commun. 2013, 12, 1958–1967. [Google Scholar] [CrossRef]
- Weiss, A. On the accuracy of a cellular location system based on RSS measurements. IEEE Trans. Veh. Technol. 2003, 52, 1508–1518. [Google Scholar] [CrossRef]
- Catovic, A.; Sahinoglu, Z. The Cramer-Rao bounds of hybrid TOA/RSS and TDOA/RSS location estimation schemes. IEEE Commun. Lett. 2004, 8, 626–628. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. RSS-Based Localization in Wireless Sensor Networks Using Convex Relaxation: Noncooperative and Cooperative Schemes. IEEE Trans. Veh. Technol. 2015, 64, 2037–2050. [Google Scholar] [CrossRef] [Green Version]
- Jin, D.; Yin, F.; Fritsche, C.; Gustafsson, F.; Zoubir, A.M. Bayesian Cooperative Localization Using Received Signal Strength with Unknown Path Loss Exponent: Message Passing Approaches. IEEE Trans. Signal Process. 2020, 68, 1120–1135. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Shu, F.; Shi, B.; Cheng, X.; Song, Y.; Wang, J. Enhanced RSS-Based UAV Localization Via Trajectory and Multi-Base Stations. IEEE Commun. Lett. 2021, 25, 1881–1885. [Google Scholar] [CrossRef]
- Lingren, A.G.; Gong, K.F. Position and Velocity Estimation Via Bearing Observations. IEEE Trans. Aerosp. Electron. Syst. 1978, AES-14, 564–577. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified Near-Field and Far-Field Localization for AOA and Hybrid AOA-TDOA Positionings. IEEE Trans. Wirel. Commun. 2018, 17, 1242–1254. [Google Scholar] [CrossRef]
- Bishop, A.N.; Anderson, B.D.O.; Fidan, B.; Pathirana, P.N.; Mao, G. Bearing-Only Localization using Geometrically Constrained Optimization. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 308–320. [Google Scholar] [CrossRef]
- Shu, F.; Yang, S.; Lu, J.; Li, J. On Impact of Earth Constraint on TDOA-Based Localization Performance in Passive Multisatellite Localization Systems. IEEE Syst. J. 2018, 12, 3861–3864. [Google Scholar] [CrossRef]
- Shu, F.; Qin, Y.; Liu, T.; Gui, L.; Zhang, Y.; Li, J.; Han, Z. Low-Complexity and High-Resolution DOA Estimation for Hybrid Analog and Digital Massive MIMO Receive Array. IEEE Trans. Commun. 2018, 66, 2487–2501. [Google Scholar] [CrossRef] [Green Version]
- Shi, B.; Jiang, X.; Chen, N.; Teng, Y.; Lu, J.; Shu, F.; Zou, J.; Li, J.; Wang, J. Fast ambiguous DOA elimination method of DOA measurement for hybrid massive MIMO receiver. Sci. China Inf. Sci. 2022, 65, 159302. [Google Scholar] [CrossRef]
- Shi, B.; Chen, N.; Zhu, X.; Qian, Y.; Zhang, Y.; Shu, F.; Wang, J. Impact of Low-Resolution ADC on DOA Estimation Performance for Massive MIMO Receive Array. IEEE Syst. J. 2022, 16, 2635–2638. [Google Scholar] [CrossRef]
- Wen, F.; Gui, G.; Gacanin, H.; Sari, H. Compressive Sampling Framework for 2D-DOA and Polarization Estimation in mmWave Polarized Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2022, 22, 3071–3083. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Tian, Z.; Leus, G.; Zhang, G. Efficient Super-Resolution Two-Dimensional Harmonic Retrieval With Multiple Measurement Vectors. IEEE Trans. Signal Process. 2022, 70, 1224–1240. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, J.A.; Zhang, X.P. A Novel Location-Penalized Maximum Likelihood Estimator for Bearing-Only Target Localization. IEEE Trans. Signal Process. 2012, 60, 6166–6181. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Cabric, D. Stansfield Localization Algorithm: Theoretical Analysis and Distributed Implementation. IEEE Wirel. Commun. Lett. 2013, 2, 327–330. [Google Scholar] [CrossRef]
- Lu, L.; Wu, H.C. Novel Robust Direction-of-Arrival-Based Source Localization Algorithm for Wideband Signals. IEEE Trans. Wirel. Commun. 2012, 11, 3850–3859. [Google Scholar] [CrossRef]
- Le Cadre, J.P.; Jaetffret, C. On the convergence of iterative methods for bearings-only tracking. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 801–818. [Google Scholar] [CrossRef] [Green Version]
- Shao, H.J.; Zhang, X.P.; Wang, Z. Efficient Closed-Form Algorithms for AOA Based Self-Localization of Sensor Nodes Using Auxiliary Variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Zhou, Q.; Duan, Z. Weighted intersections of bearing lines for AOA based localization. In Proceedings of the 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014; pp. 1–8. [Google Scholar]
- Dogancay, K.; Ibal, G. Instrumental Variable Estimator for 3D Bearings-Only Emitter Localization. In Proceedings of the 2005 International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, VIC, Australia, 5–8 December 2005; pp. 63–68. [Google Scholar]
- Doğancay, K. 3D Pseudolinear Target Motion Analysis From Angle Measurements. IEEE Trans. Signal Process. 2015, 63, 1570–1580. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Gui, G.; Gacanin, H.; Dobre, O.A. 3-D Positioning Method for Anonymous UAV Based on Bistatic Polarized MIMO Radar. IEEE Internet Things J. 2023, 10, 815–827. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G.; Coviello, G. Multiple Source Angle of Arrival Estimation Through Phase Interferometry. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 674–678. [Google Scholar] [CrossRef]
- Gou, P.; Li, F.; Wang, Y.; Li, M. Low Energy Consumption and High-Precision Time Synchronization Algorithm Based on Improved TPSN in Wireless Sensor Networks. In Proceedings of the 2018 International Conference on Engineering Simulation and Intelligent Control (ESAIC), Changsha, China, 10–11 August 2018; pp. 54–57. [Google Scholar]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. ACM SIGOPS Oper. Syst. Rev. 2002, 36, 147–163. [Google Scholar] [CrossRef] [Green Version]
- BniLam, N.; Nasser, S.; Weyn, M. Angle of Arrival Estimation System for LoRa Technology based on Phase Detectors. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–5. [Google Scholar]
- Palomar, D.P.; Eldar, Y.C. Convex Optimization in Signal Processing and Communications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing; PTR Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Badriasl, L.; Dogancay, K. Three-dimensional target motion analysis using azimuth/elevation angles. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3178–3194. [Google Scholar] [CrossRef]


| Methods | Advantages | Disadvantages |
|---|---|---|
| RSS | 1. Low circuit cost 2. Easy to be implemented | Performance is easily influenced by electromagnetic energy |
| TOA | 1. The speed of light is fixed 2. Interfered with by the structure of array | Requires ultra-high-precision time measurement synchronization accuracy |
| AOA | Relatively low communications cost | Multiple antennas are essential |
| Algorithms | Complexity |
|---|---|
| Conventional LS | |
| MLE in [19] | |
| BR-PLE in [2] | |
| Proposed CIS | |
| Proposed MSD-LS |
| Parameter | Value |
|---|---|
| Source location | m |
| The range of UAVs’ locations | m |
| The number of UAVs | 20 |
| Angle measurement variance | −5 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, B.; Li, Y.; Wu, G.; Chen, R.; Yan, S.; Shu, F. Low-Complexity Three-Dimensional AOA-Cross Geometric Center Localization Methods via Multi-UAV Network. Drones 2023, 7, 318. https://doi.org/10.3390/drones7050318
Shi B, Li Y, Wu G, Chen R, Yan S, Shu F. Low-Complexity Three-Dimensional AOA-Cross Geometric Center Localization Methods via Multi-UAV Network. Drones. 2023; 7(5):318. https://doi.org/10.3390/drones7050318
Chicago/Turabian StyleShi, Baihua, Yifan Li, Guilu Wu, Riqing Chen, Shihao Yan, and Feng Shu. 2023. "Low-Complexity Three-Dimensional AOA-Cross Geometric Center Localization Methods via Multi-UAV Network" Drones 7, no. 5: 318. https://doi.org/10.3390/drones7050318
APA StyleShi, B., Li, Y., Wu, G., Chen, R., Yan, S., & Shu, F. (2023). Low-Complexity Three-Dimensional AOA-Cross Geometric Center Localization Methods via Multi-UAV Network. Drones, 7(5), 318. https://doi.org/10.3390/drones7050318










