Stepwise Soft Actor–Critic for UAV Autonomous Flight Control
Abstract
:1. Introduction
- In this study, we constructed realistic flight environments based on JSBSim, a 6-DOF flight environment with high-dimensional state and action spaces;
- We define states, actions, and rewards for the UAV agent to successfully accomplish disaster management and counter-terrorism missions. We incorporated past experiences by stacking the states of previous time steps into the states by utilizing a 1D convolution layer. Additionally, we customized the episode rewards and time step rewards to match the specific characteristics of each mission;
- We introduce a positive buffer and a cool-down alpha technique into the SAC algorithm to improve learning efficiency and stability;
- Finally, we propose SeSAC by incorporating the concept of stepwise learning. Throughout the experiments, it was confirmed that the agent trained with SeSAC succeeded in the mission with fewer learning epochs and a higher average reward.
2. Background
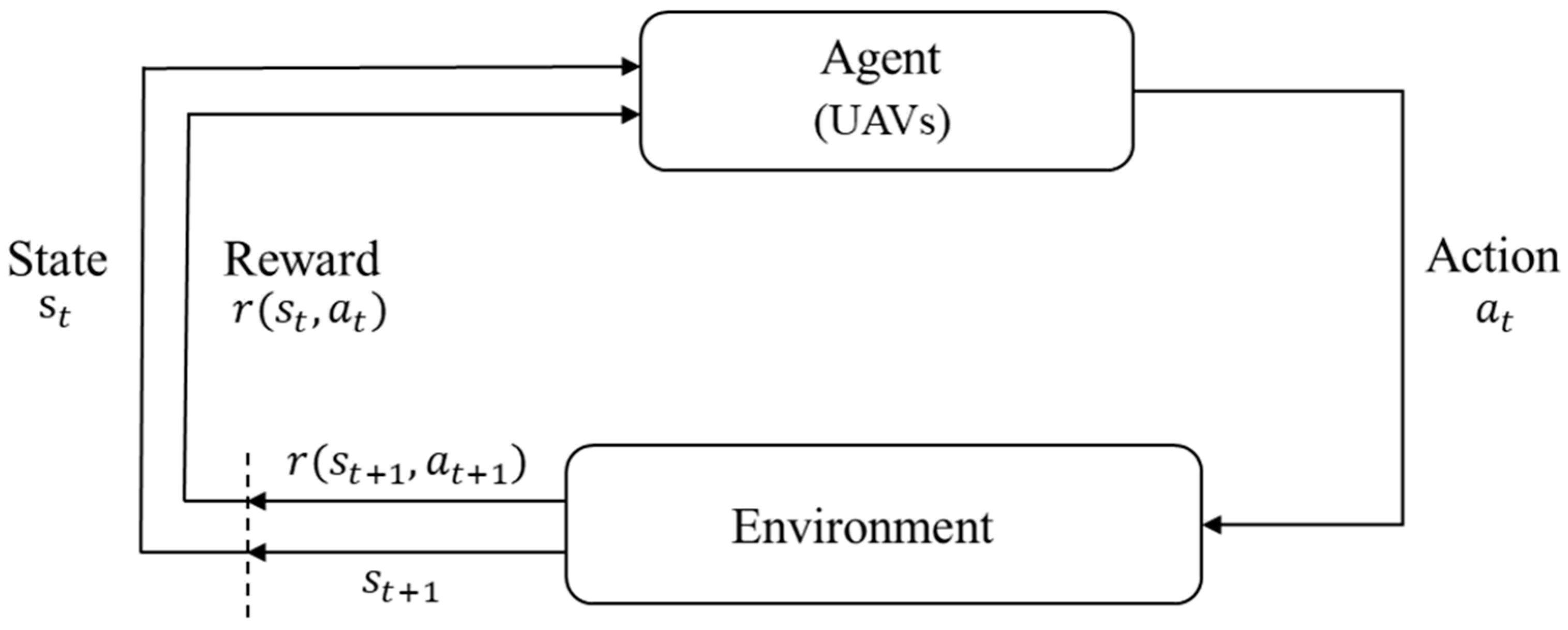
2.1. Reinforcement Learning
2.2. Actor–Critic Algorithm
2.3. Soft Actor–Critic
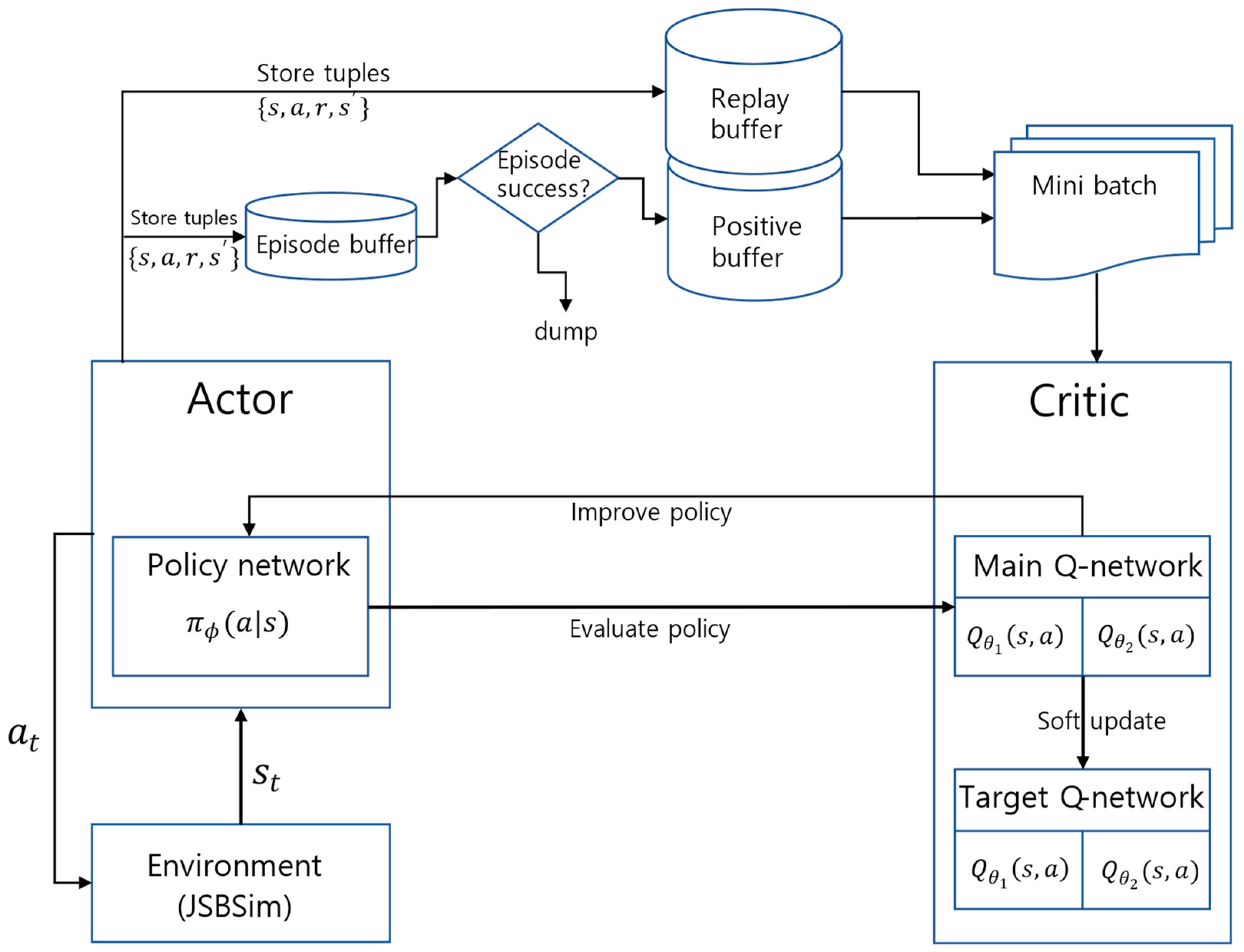
3. Proposed Method
3.1. Positive Buffer
3.2. Cool-Down Alpha
| Algorithm 1: Soft Actor–Critic + Positive Buffer + Cool-down alpha |
Initialize main Q-network weights , and policy network weight Initialize target Q-network weights , Initialize replay and positive buffer Initialize episode buffer Update Q-function parameters Update policy weights Update target network weights Adjust temperature parameter |
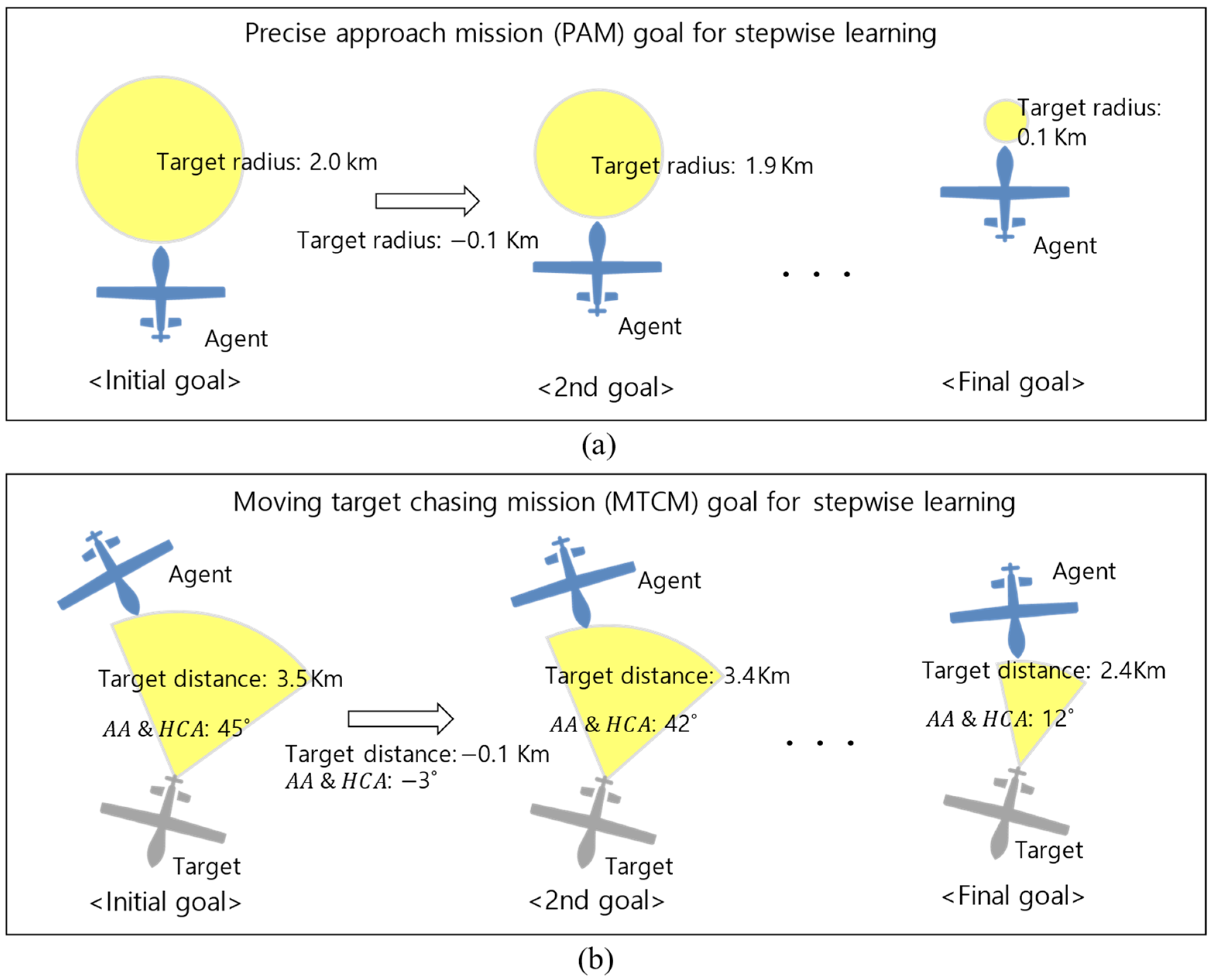
3.3. Stepwise Soft Actor–Critic
| Algorithm 2: Stepwise soft actor–critic (SeSAC) |
3.4. Environment and Agent Design
3.4.1. Environment
3.4.2. States
3.4.3. Actions
3.4.4. Reward
- Distance reward: Reward for the difference between the distance from the target at timestep and the distance from the target at timestep . This induces the agent to approach the target without moving away from it;
- Line-of-sight (LOS) reward: Reward increases as the agent’s heading direction accurately faces the target in three-dimensional space. It consists of the pitch score and heading score, which are calculated based on the pitch angle and heading angle to the target, respectively.
4. Experiments
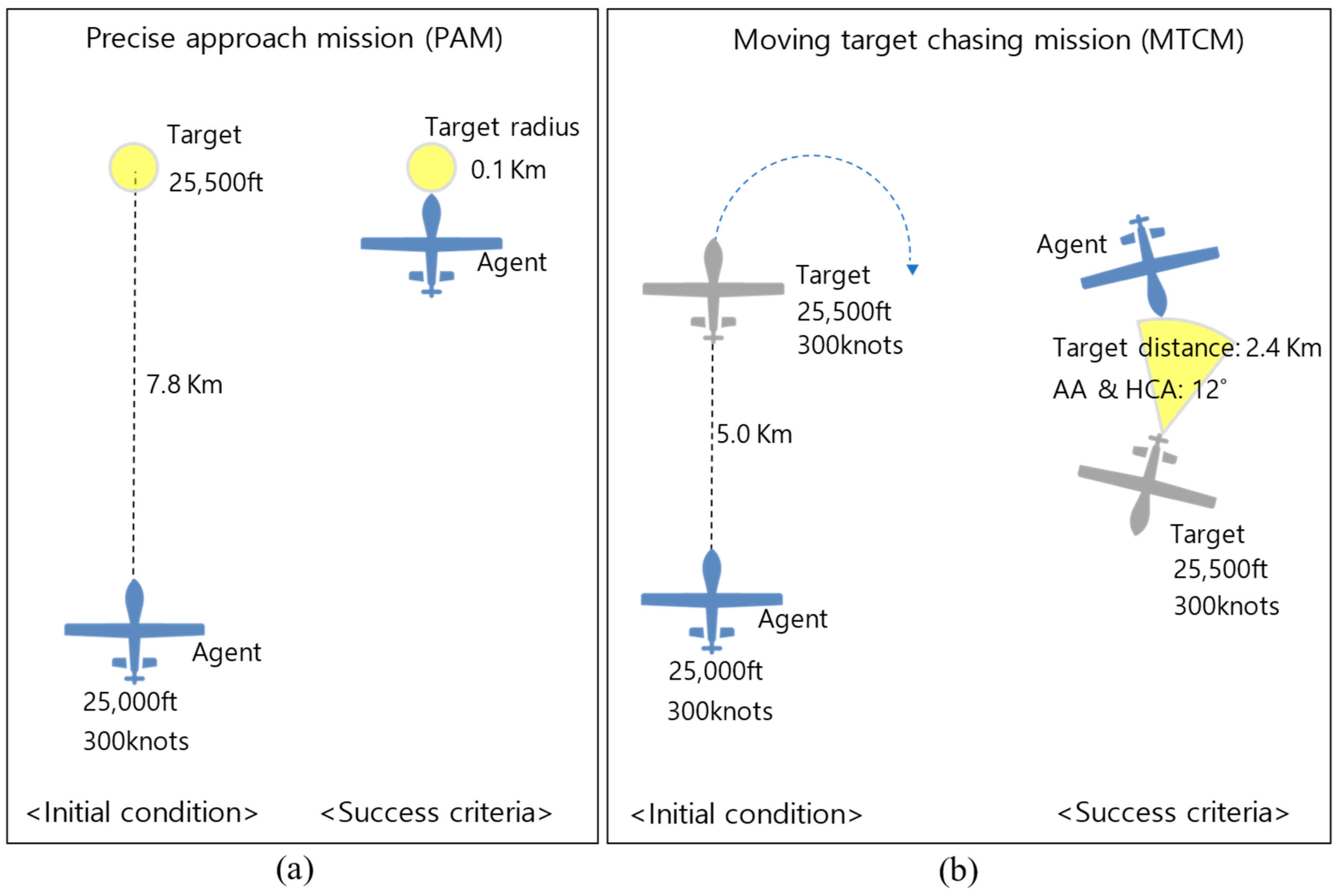
4.1. Experiment Design
4.1.1. Reward Function for PAM
- Success reward: This reward represents the success condition of the mission and is given as a reward of 500 when ;
- Failure reward: This reward is received by −100 when , which means the agent failed the mission by colliding with the ground or overtaking the target;
- Distance reward: The agent receives a value of at every timestep. This reward becomes negative when the agent is farther away from the target and positive when it is closer.
4.1.2. Reward Function for MTCM
- Success reward: This reward of 100 is given when . Additionally, if the agent satisfies these conditions consecutively for five timesteps, it is considered a success.
- LOS reward: As the agent’s gaze moves further away from the target, it receives a smaller reward, as follows
- Failure and Distance reward: Same as PAM’s Failure and Distance reward.
4.1.3. Model Structure and Hyperparameters
4.2. Experiment Results
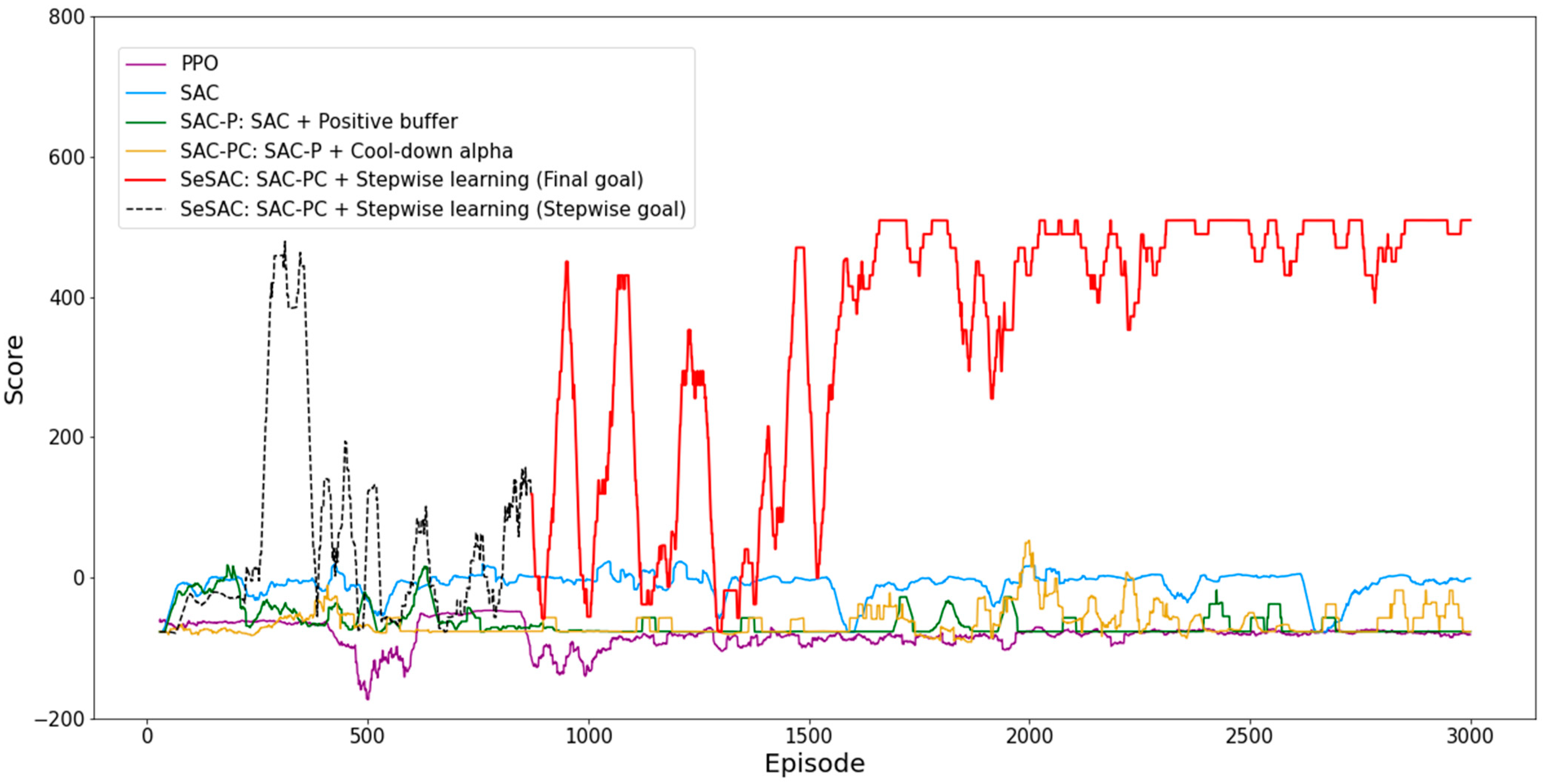
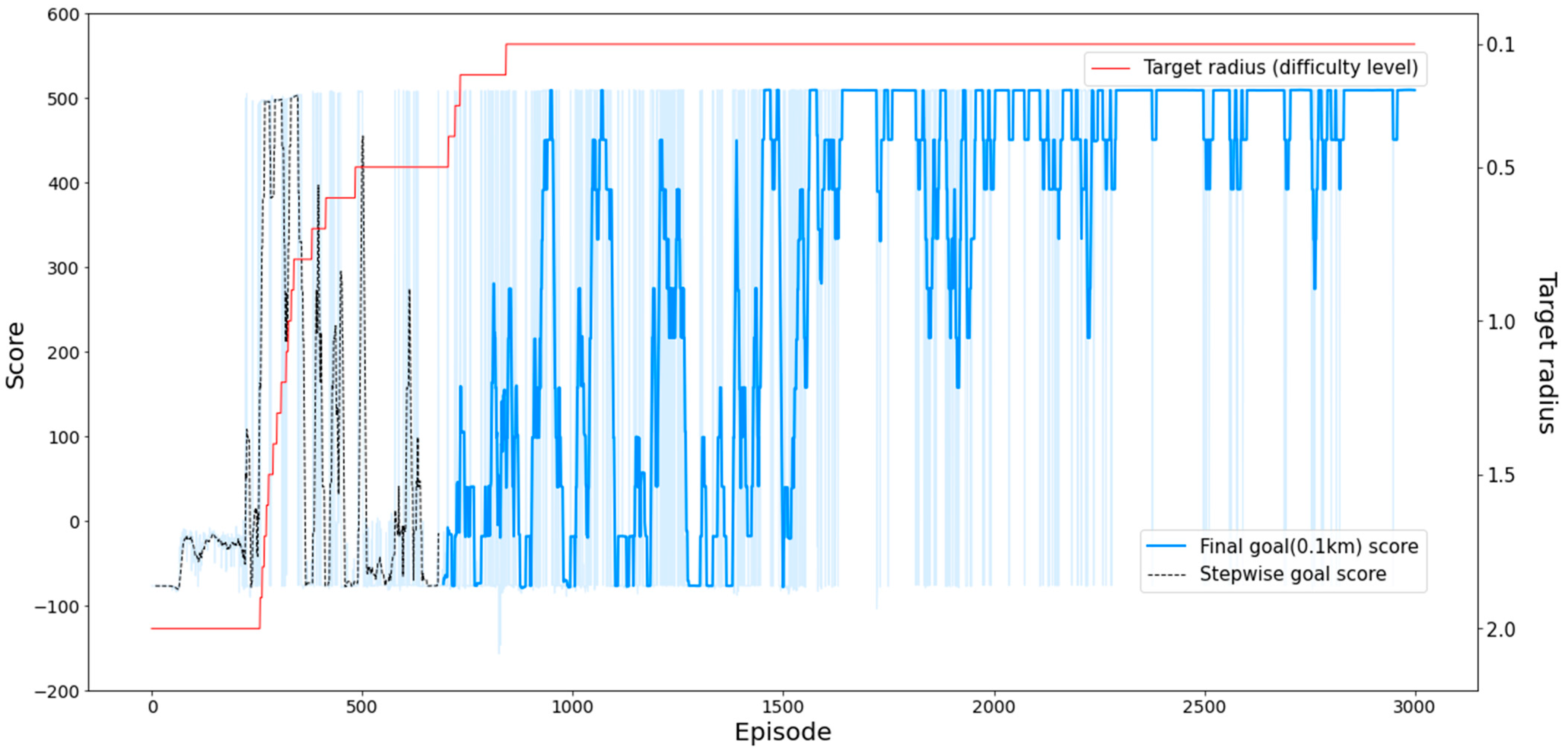
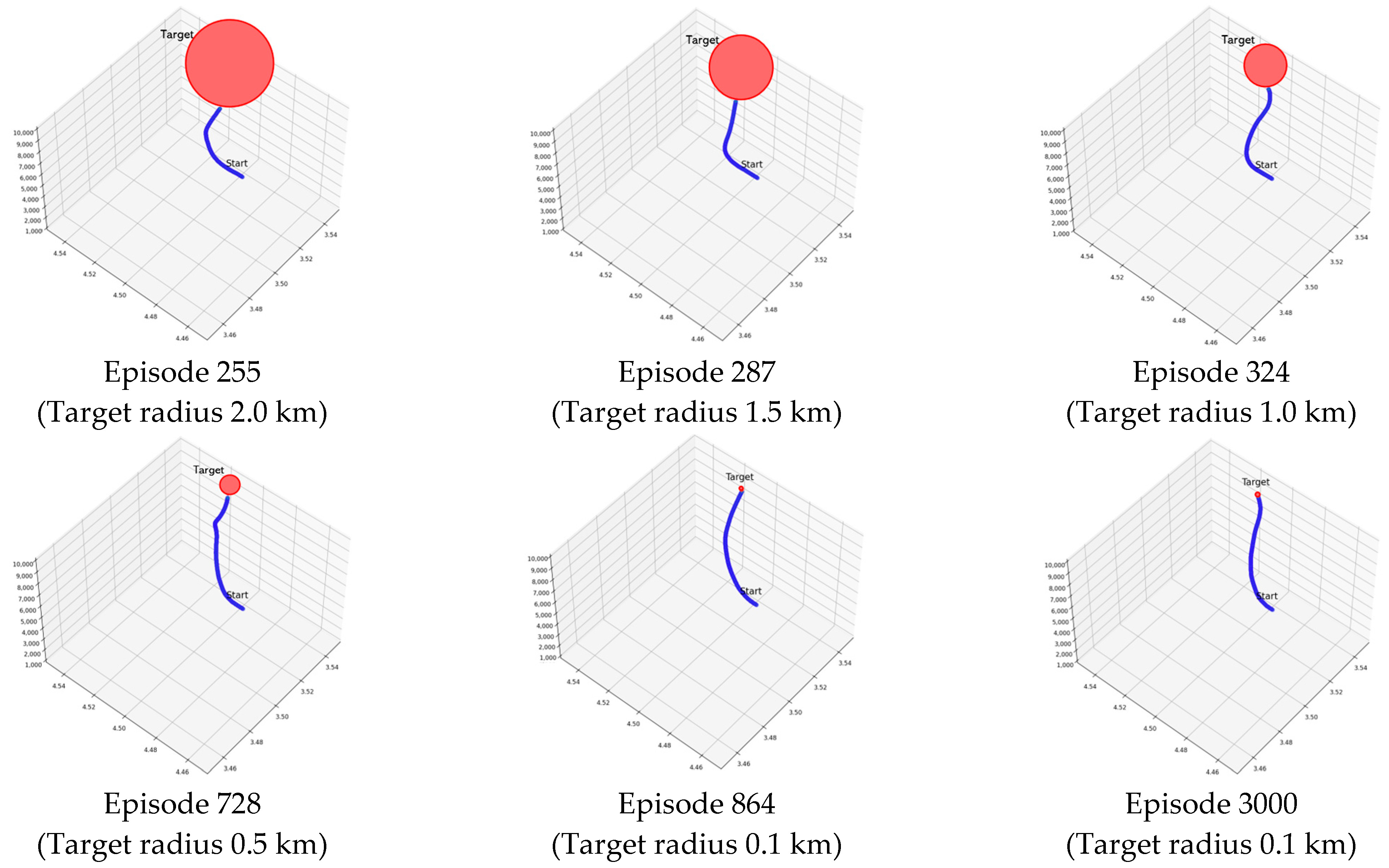
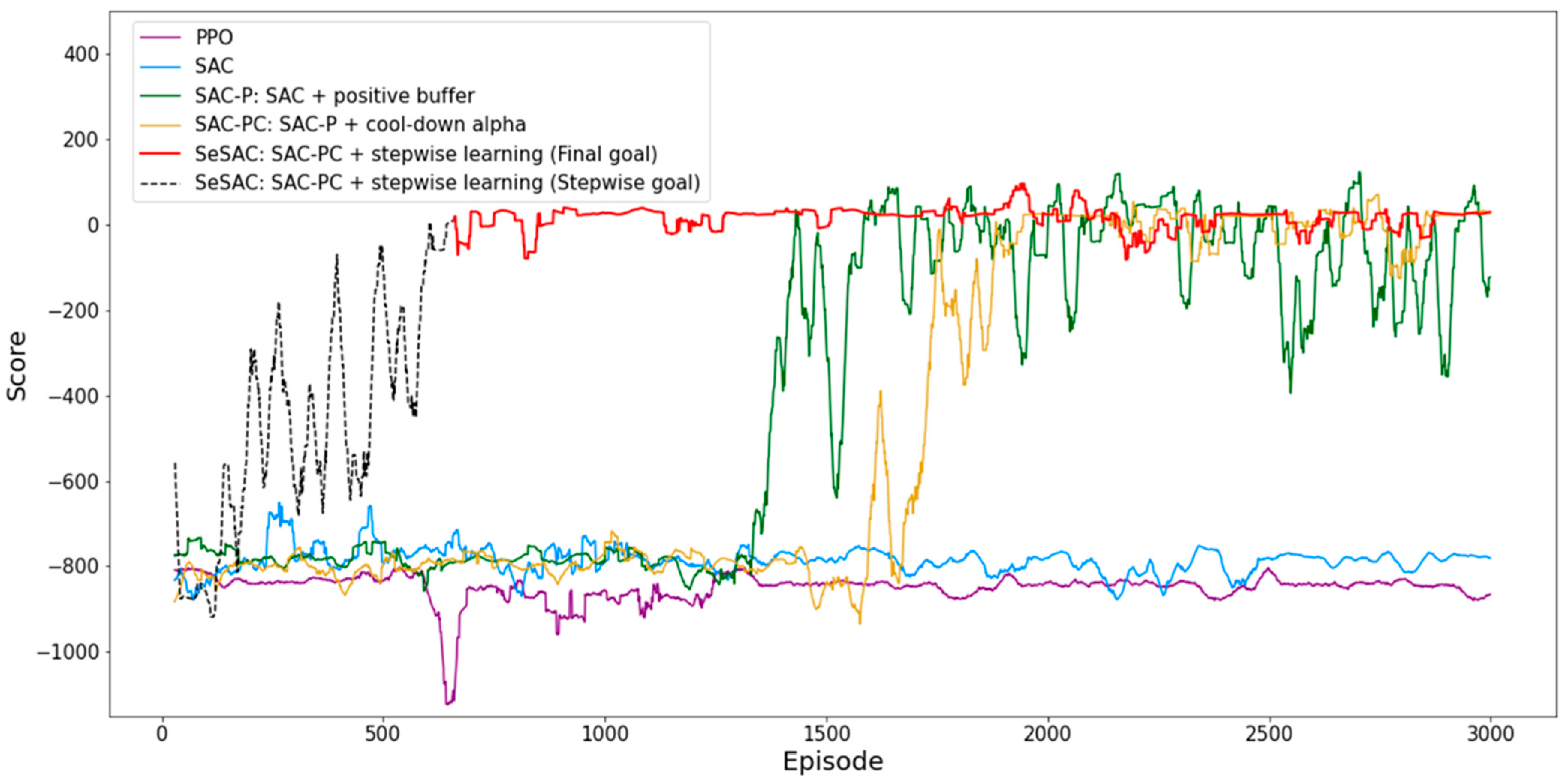
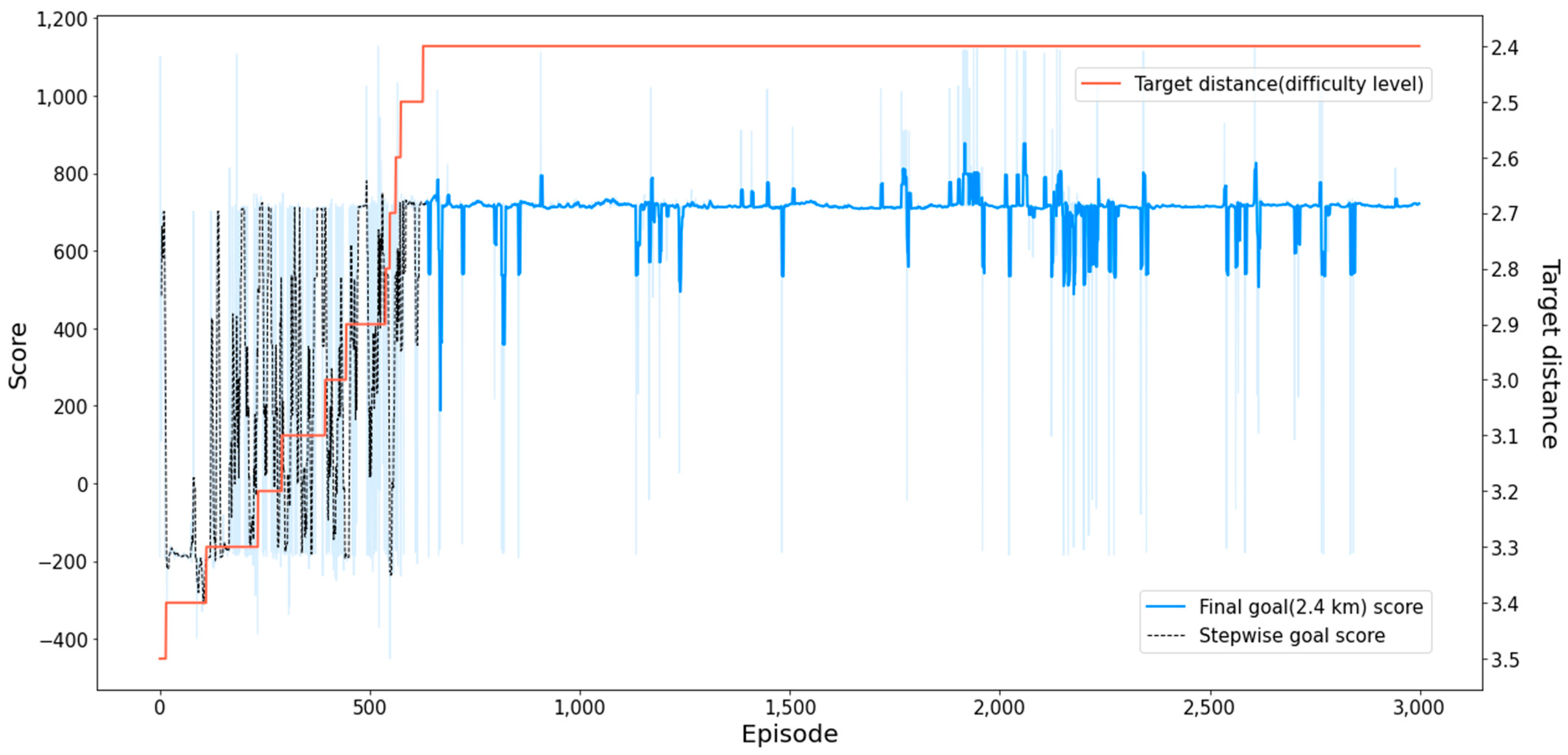
4.2.1. Result for PAM
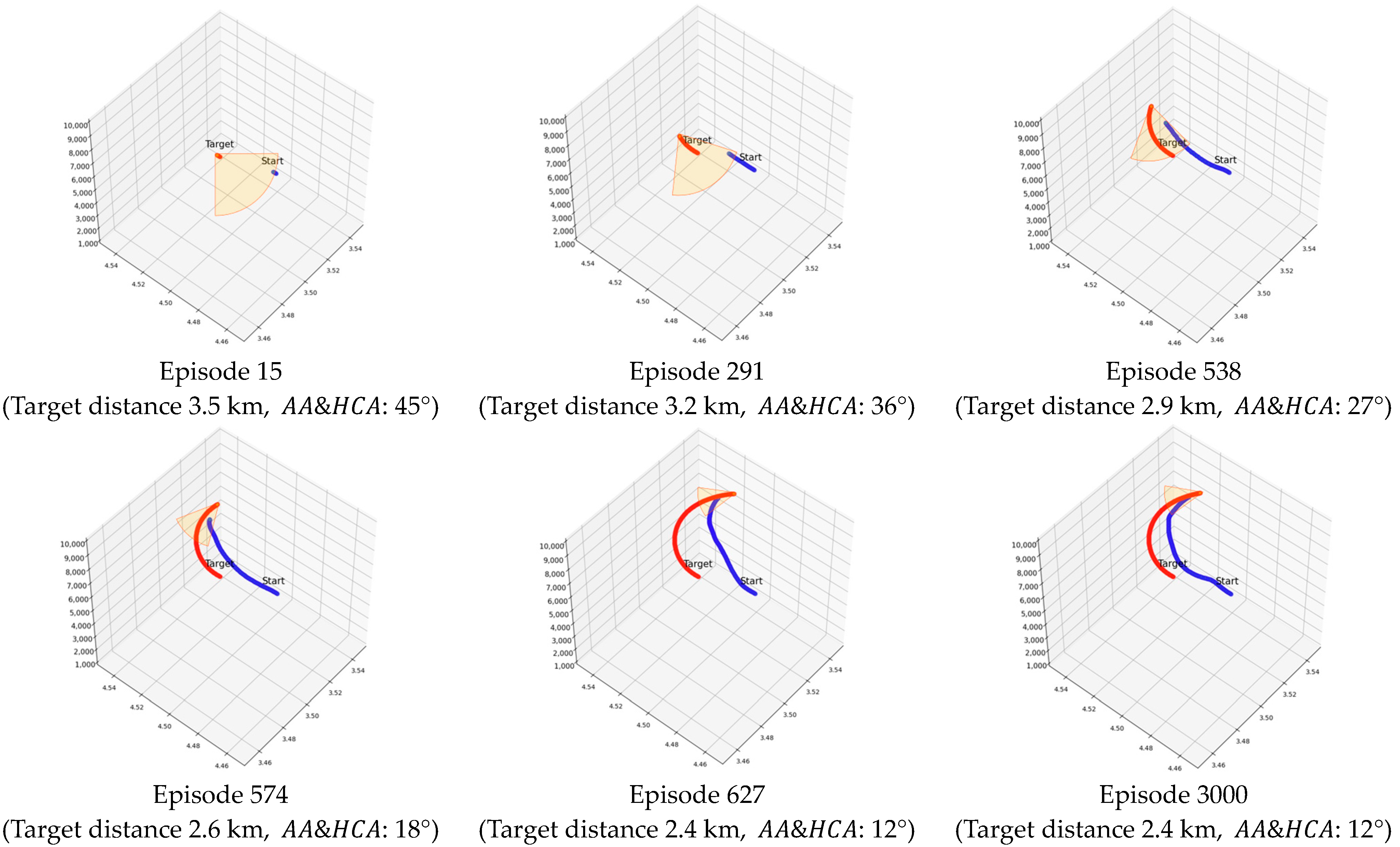
4.2.2. Result for MTCM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV Photogrammetry for Mapping and 3d Modeling: Current Status and Future Perspectives. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 25–31. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The Application of Small Unmanned Aerial Systems for Precision Agriculture: A Review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Gomez, C.; Purdie, H. UAV-Based Photogrammetry and Geocomputing for Hazards and Disaster Risk Monitoring—A Review. Geoenviron. Disasters 2016, 3, 23. [Google Scholar] [CrossRef]
- Ling, G.; Draghic, N. Aerial Drones for Blood Delivery. Transfusion 2019, 59, 1608–1611. [Google Scholar] [CrossRef] [PubMed]
- Hii, M.S.Y.; Courtney, P.; Royall, P.G. An Evaluation of the Delivery of Medicines Using Drones. Drones 2019, 3, 52. [Google Scholar] [CrossRef]
- Gong, S.; Wang, M.; Gu, B.; Zhang, W.; Hoang, D.T.; Niyato, D. Bayesian Optimization Enhanced Deep Reinforcement Learning for Trajectory Planning and Network Formation in Multi-UAV Networks. IEEE Trans. Veh. Technol. 2023, 1–16. [Google Scholar] [CrossRef]
- Bose, T.; Suresh, A.; Pandey, O.J.; Cenkeramaddi, L.R.; Hegde, R.M. Improving Quality-of-Service in Cluster-Based UAV-Assisted Edge Networks. IEEE Trans. Netw. Serv. Manag. 2022, 19, 1903–1919. [Google Scholar] [CrossRef]
- Yeduri, S.R.; Chilamkurthy, N.S.; Pandey, O.J.; Cenkeramaddi, L.R. Energy and Throughput Management in Delay-Constrained Small-World UAV-IoT Network. IEEE Internet Things J. 2023, 10, 7922–7935. [Google Scholar] [CrossRef]
- Kingston, D.; Rasmussen, S.; Humphrey, L. Automated UAV Tasks for Search and Surveillance. In Proceedings of the IEEE Conference on Control Applications, Buenos Aires, Argentina, 19–22 September 2016. [Google Scholar]
- Motlagh, N.H.; Bagaa, M.; Taleb, T. IEEE Communications Magazine; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2017; pp. 128–134. [Google Scholar]
- Masadeh, A.; Alhafnawi, M.; Salameh, H.A.B.; Musa, A.; Jararweh, Y. Reinforcement Learning-Based Security/Safety UAV System for Intrusion Detection Under Dynamic and Uncertain Target Movement. IEEE Trans. Eng. Manag. 2022, 1–11. [Google Scholar] [CrossRef]
- Tian, J.; Wang, B.; Guo, R.; Wang, Z.; Cao, K.; Wang, X. Adversarial Attacks and Defenses for Deep-Learning-Based Unmanned Aerial Vehicles. IEEE Internet Things J. 2022, 9, 22399–22409. [Google Scholar] [CrossRef]
- Azar, A.T.; Koubaa, A.; Ali Mohamed, N.; Ibrahim, H.A.; Ibrahim, Z.F.; Kazim, M.; Ammar, A.; Benjdira, B.; Khamis, A.M.; Hameed, I.A.; et al. Drone Deep Reinforcement Learning: A Review. Electronics 2021, 10, 999. [Google Scholar] [CrossRef]
- Davies, L.; Vagapov, Y.; Bolam, R.C.; Anuchin, A. Review of Unmanned Aircraft System Technologies to Enable beyond Visual Line of Sight (BVLOS) Operations. In Proceedings of the International Conference on Electrical Power Drive Systems (ICEPDS), Novocherkassk, Russia, 3–6 October 2018; pp. 1–6. [Google Scholar]
- Chen, H.; Wang, X.M.; Li, Y. A Survey of Autonomous Control for UAV. In Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence (AICI), Shanghai, China, 7–8 November 2009; Volume 2, pp. 267–271. [Google Scholar]
- Darbari, V.; Gupta, S.; Verman, O.P. Dynamic Motion Planning for Aerial Surveillance on a Fixed-Wing UAV. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 488–497. [Google Scholar]
- Polo, J.; Hornero, G.; Duijneveld, C.; García, A.; Casas, O. Design of a Low-Cost Wireless Sensor Network with UAV Mobile Node for Agricultural Applications. Comput. Electron. Agric. 2015, 119, 19–32. [Google Scholar] [CrossRef]
- Hoa, S.; Abdali, M.; Jasmin, A.; Radeschi, D.; Prats, V.; Faour, H.; Kobaissi, B. Development of a New Flexible Wing Concept for Unmanned Aerial Vehicle Using Corrugated Core Made by 4D Printing of Composites. Compos. Struct. 2022, 290, 115444. [Google Scholar] [CrossRef]
- Prisacariu, V.; Boscoianu, M.; Circiu, I.; Rau, C.G. Applications of the Flexible Wing Concept at Small Unmanned Aerial Vehicles. Adv. Mater. Res. 2012, 463, 1564–1567. [Google Scholar]
- Boris, V.; Jérôme, D.M.; Stéphane, B. A Two Rule-Based Fuzzy Logic Controller for Contrarotating Coaxial Rotors UAV. In Proceedings of the IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 16–21 July 2006; pp. 1563–1569. [Google Scholar]
- Oh, H.; Shin, H.-S.; Kim, S. Fuzzy Expert Rule-Based Airborne Monitoring of Ground Vehicle Behaviour. In Proceedings of the UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 534–539. [Google Scholar]
- Çolak, M.; Kaya, İ.; Karaşan, A.; Erdoğan, M. Two-Phase Multi-Expert Knowledge Approach by Using Fuzzy Clustering and Rule-Based System for Technology Evaluation of Unmanned Aerial Vehicles. Neural. Comput. Appl. 2022, 34, 5479–5495. [Google Scholar] [CrossRef]
- Toubman, A.; Roessingh, J.J.; Spronck, P.; Plaat, A.; van den Herik, J. Rapid Adaptation of Air Combat Behaviour; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Teng, T.H.; Tan, A.H.; Tan, Y.S.; Yeo, A. Self-Organizing Neural Networks for Learning Air Combat Maneuvers. In Proceedings of the Proceedings of the International Joint Conference on Neural Networks, Brisbane, QLD, Australia, 10–15 June 2012. [Google Scholar]
- Pope, A.P.; Ide, J.S.; Micovic, D.; Diaz, H.; Rosenbluth, D.; Ritholtz, L.; Twedt, J.C.; Walker, T.T.; Alcedo, K.; Javorsek, D. Hierarchical Reinforcement Learning for Air-to-Air Combat. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2021; pp. 275–284. [Google Scholar]
- Chen, Y.; Zhang, J.; Yang, Q.; Zhou, Y.; Shi, G.; Wu, Y. Design and Verification of UAV Maneuver Decision Simulation System Based on Deep Q-Learning Network. In Proceedings of the IEEE International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020; pp. 817–823. [Google Scholar]
- Xu, J.; Guo, Q.; Xiao, L.; Li, Z.; Zhang, G. Autonomous Decision-Making Method for Combat Mission of UAV Based on Deep Reinforcement Learning. In Proceedings of the IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 20–22 December 2019; pp. 538–544. [Google Scholar]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver Decision of UAV in Short-Range Air Combat Based on Deep Reinforcement Learning. IEEE Access 2020, 8, 363–378. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Wu, H.; Wu, Z. Improving Maneuver Strategy in Air Combat by Alternate Freeze Games with a Deep Reinforcement Learning Algorithm. Math. Probl. Eng. 2020, 2020, 7180639. [Google Scholar] [CrossRef]
- Lee, G.T.; Kim, C.O. Autonomous Control of Combat Unmanned Aerial Vehicles to Evade Surface-to-Air Missiles Using Deep Reinforcement Learning. IEEE Access 2020, 8, 226724–226736. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Fixed-Wing UAVs Flocking in Continuous Spaces: A Deep Reinforcement Learning Approach. Rob Auton. Syst. 2020, 131, 103594. [Google Scholar] [CrossRef]
- Bohn, E.; Coates, E.M.; Moe, S.; Johansen, T.A. Deep Reinforcement Learning Attitude Control of Fixed-Wing UAVs Using Proximal Policy Optimization. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 523–533. [Google Scholar]
- Tang, C.; Lai, Y.C. Deep Reinforcement Learning Automatic Landing Control of Fixed-Wing Aircraft Using Deep Deterministic Policy Gradient. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020; pp. 1–9. [Google Scholar]
- Yuan, X.; Sun, Y.; Wang, Y.; Sun, C. Deterministic Policy Gradient with Advantage Function for Fixed Wing UAV Automatic Landing. In Proceedings of the Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8305–8310. [Google Scholar]
- Rocha, T.A.; Anbalagan, S.; Soriano, M.L.; Chaimowicz, L. Algorithms or Actions? A Study in Large-Scale Reinforcement Learning. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI-18), Stockholm, Sweden, 13–19 July 2018; pp. 2717–2723. [Google Scholar]
- Imanberdiyev, N.; Fu, C.; Kayacan, E.; Chen, I.M. Autonomous Navigation of UAV by Using Real-Time Model-Based Reinforcement Learning. In Proceedings of the International Conference on Control, Automation, Robotics and Vision, ICARCV 2016, Phuket, Thailand, 13–15 November 2016; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2017. [Google Scholar]
- Wang, C.; Wang, J.; Wang, J.; Zhang, X. Deep-Reinforcement-Learning-Based Autonomous UAV Navigation with Sparse Rewards. IEEE Internet Things J. 2020, 7, 6180–6190. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Shen, Y.; Zhang, X. Autonomous Navigation of UAVs in Large-Scale Complex Environments: A Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2019, 68, 2124–2136. [Google Scholar] [CrossRef]
- Berndt, J.S. JSBSim: An Open Source Flight Dynamics Model in C++. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Providence, Rhode Island, 16–19 August 2004. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Dong, H.; Ding, Z.; Zhang, S. Deep Reinforcement Learning; Springer: Singapore, 2020; ISBN 978-981-15-4095-0. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. IEEE Signal Processing Magazine; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2017; pp. 26–38. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-Critic Algorithms. In Advances in Neural Information Processing Systems 12 (NIPS 1999); MIT Press: Cambridge, MA, USA, 1999; Volume 12. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft Actor-Critic Algorithms and Applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Rennie, G. Autonomous Control of Simulated Fixed Wing Aircraft Using Deep Reinforcement Learning. Master’s. Thesis, The University of Bath, Bath, UK, 2018. [Google Scholar]
- Wiering, M.A.; Van Otterlo, M. Reinforcement Learning: State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 9783642015267. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D Convolutional Neural Networks and Applications: A Survey. Mech. Syst. Signal. Process 2021, 151, 107398. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction Second Edition; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
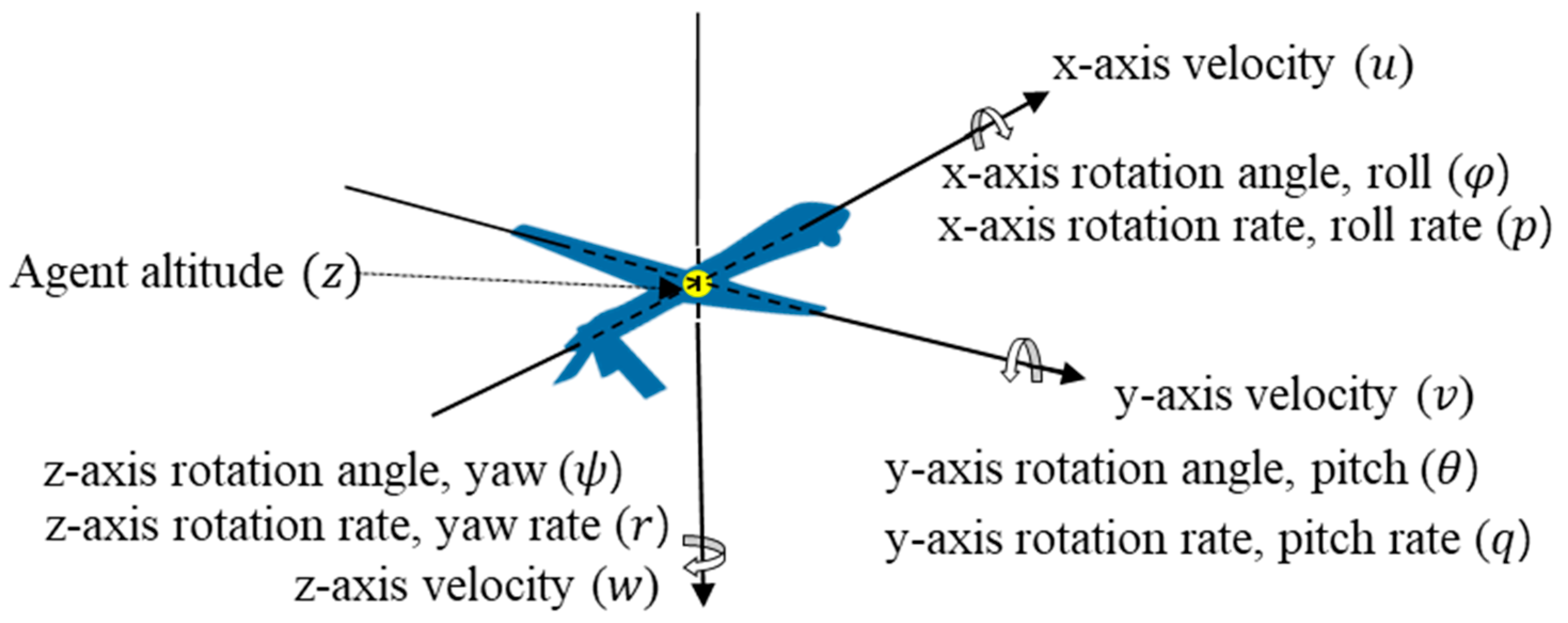
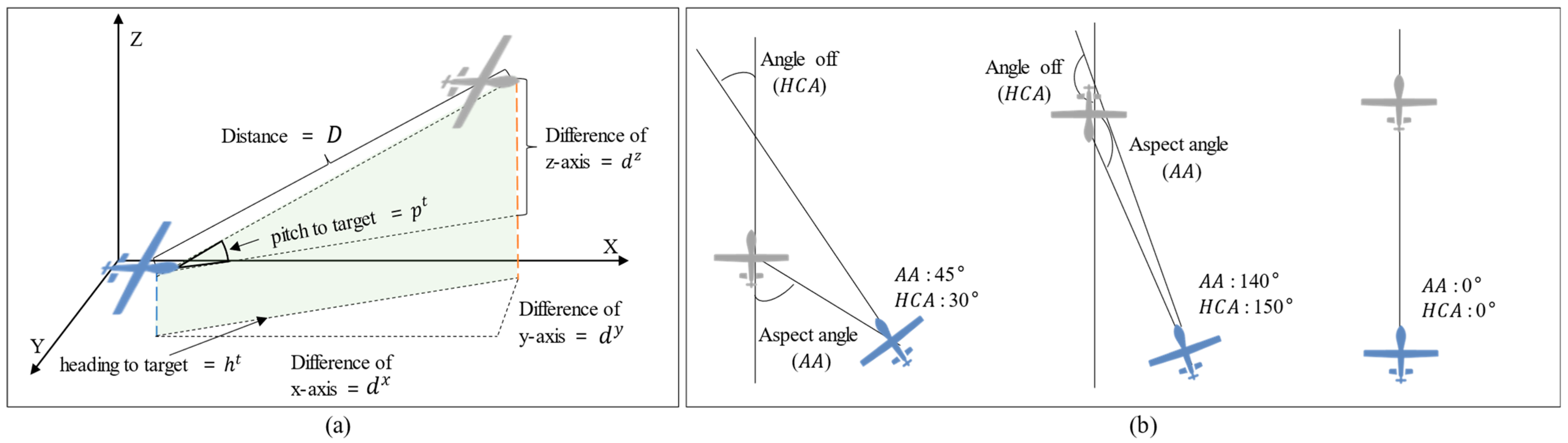
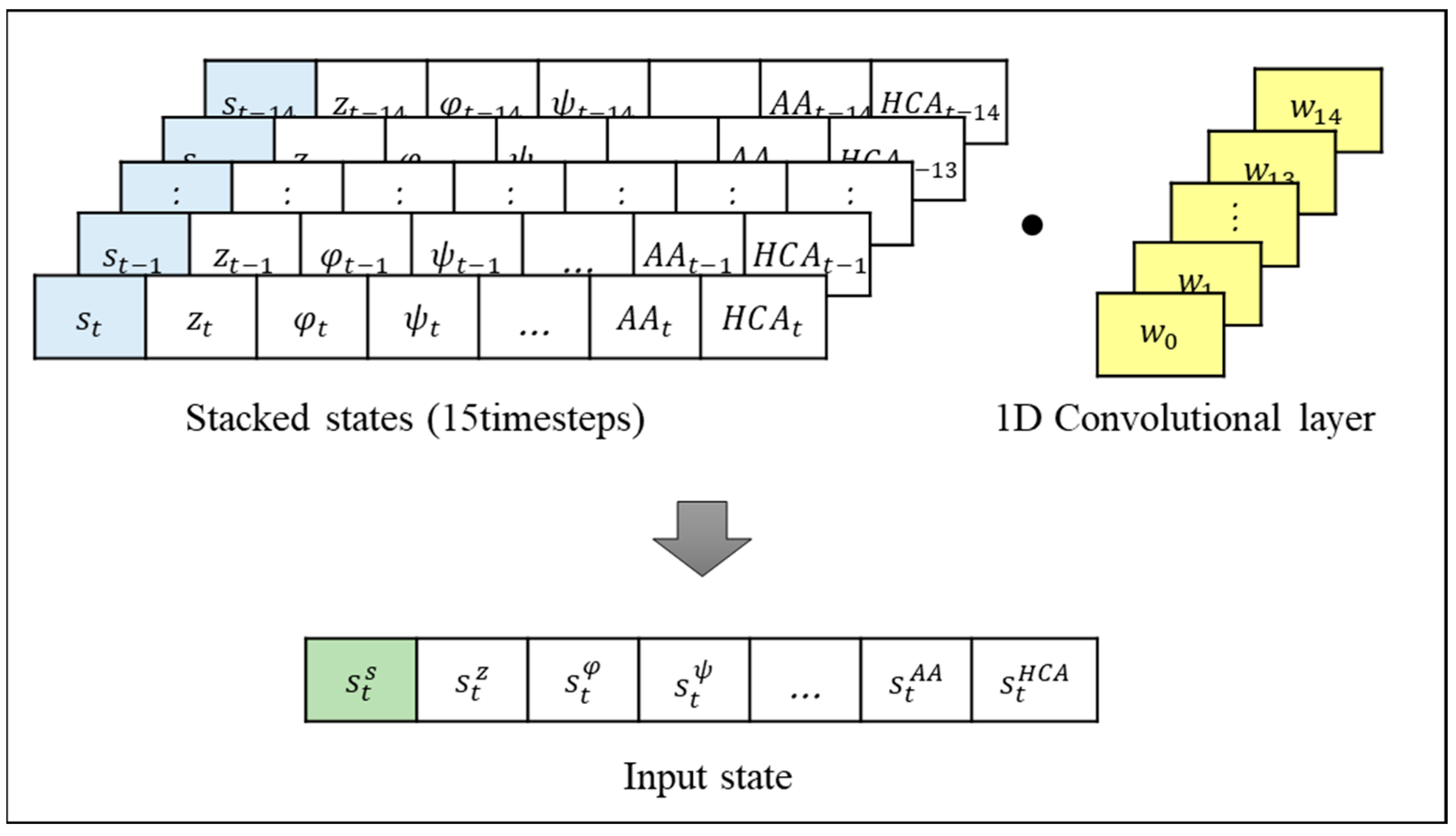
| State | Definition | State | Definition |
|---|---|---|---|
| z-axis position | z-axis rotation rate | ||
| x-axis rotation angle | Difference in x-axis position | ||
| y-axis rotation angle | Difference in y-axis position | ||
| z-axis rotation angle | Difference of z-axis position | ||
| x-axis velocity | Pitch angle to target | ||
| y-axis velocity | Heading angle to target | ||
| z-axis velocity | Distance between agent and target | ||
| x-axis rotation rate | Aspect angle | ||
| y-axis rotation rate | Heading cross angle |
| Action | Definition | Action | Definition |
|---|---|---|---|
| X-axis stick position (−1–1) | Throttle angle (0–1) | ||
| Y-axis stick position (−1–1) | Rudder pedal angle (−1–1) |
| Hyperparameter | Value | Hyperparameter | Value |
|---|---|---|---|
| Optimizer | Adam | ||
| The learning rate for actor network | Activation function | SeLU | |
| The learning rate for critic network | Replay buffer capacity | ||
| Batch size | 128 | Positive buffer capacity | |
| Configuration of hidden layers | [128, 64, 32, 32] |
| Hyperparameter | PAM | MTCM |
|---|---|---|
| 50 | 50 | |
| 0.01 | 0.01 | |
| 490 | 490 | |
| Target radius: 0.1 km | Target distance: 2.4 km, : 12° | |
| Target radius: 2.0 km | Target distance: 3.5 km, : 45° | |
| Target radius: −0.1 km | Target distance: −0.1 km, : −3° | |
| Five episodes | Ten episodes |
| Min Score | Max Score | Mean Score | Cumulative Successes | |
|---|---|---|---|---|
| PPO | −555.33 | −47.91 | −68.96 | 0 |
| SAC | −133.42 | 509.82 | −9.73 | 9 |
| SAC-P | −124.53 | 510.20 | −64.85 | 17 |
| SAC-PC | −134.33 | 511.00 | −64.03 | 62 |
| SeSAC (entire) | −157.05 | 509.85 | 274.33 | 1781 |
| SeSAC (final goal) | −157.05 | 509.85 | 338.31 | 1640 |
| Min Score | Max Score | Mean Score | Cumulative Successes | First Convergent Episode | |
|---|---|---|---|---|---|
| PPO | −2303.86 | 72.70 | −359.96 | 2 | - |
| SAC | −665.86 | 984.03 | −296.78 | 22 | - |
| SAC-P | −728.24 | 1829.24 | 95.21 | 1387 | 1602 |
| SAC-PC | −638.35 | 1120.11 | 28.62 | 1246 | 1951 |
| SeSAC (entire) | −650.34 | 928.17 | 404.90 | 2584 | 660 |
| SeSAC (final goal) | −391.14 | 927.32 | 505.99 | 2308 | 660 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, H.J.; Jang, J.; Choi, J.; Bae, J.H.; Kim, S.H.; Kim, C.O. Stepwise Soft Actor–Critic for UAV Autonomous Flight Control. Drones 2023, 7, 549. https://doi.org/10.3390/drones7090549
Hwang HJ, Jang J, Choi J, Bae JH, Kim SH, Kim CO. Stepwise Soft Actor–Critic for UAV Autonomous Flight Control. Drones. 2023; 7(9):549. https://doi.org/10.3390/drones7090549
Chicago/Turabian StyleHwang, Ha Jun, Jaeyeon Jang, Jongkwan Choi, Jung Ho Bae, Sung Ho Kim, and Chang Ouk Kim. 2023. "Stepwise Soft Actor–Critic for UAV Autonomous Flight Control" Drones 7, no. 9: 549. https://doi.org/10.3390/drones7090549
APA StyleHwang, H. J., Jang, J., Choi, J., Bae, J. H., Kim, S. H., & Kim, C. O. (2023). Stepwise Soft Actor–Critic for UAV Autonomous Flight Control. Drones, 7(9), 549. https://doi.org/10.3390/drones7090549






