Grid Matrix-Based Ground Risk Map Generation for Unmanned Aerial Vehicles in Urban Environments
Abstract
1. Introduction
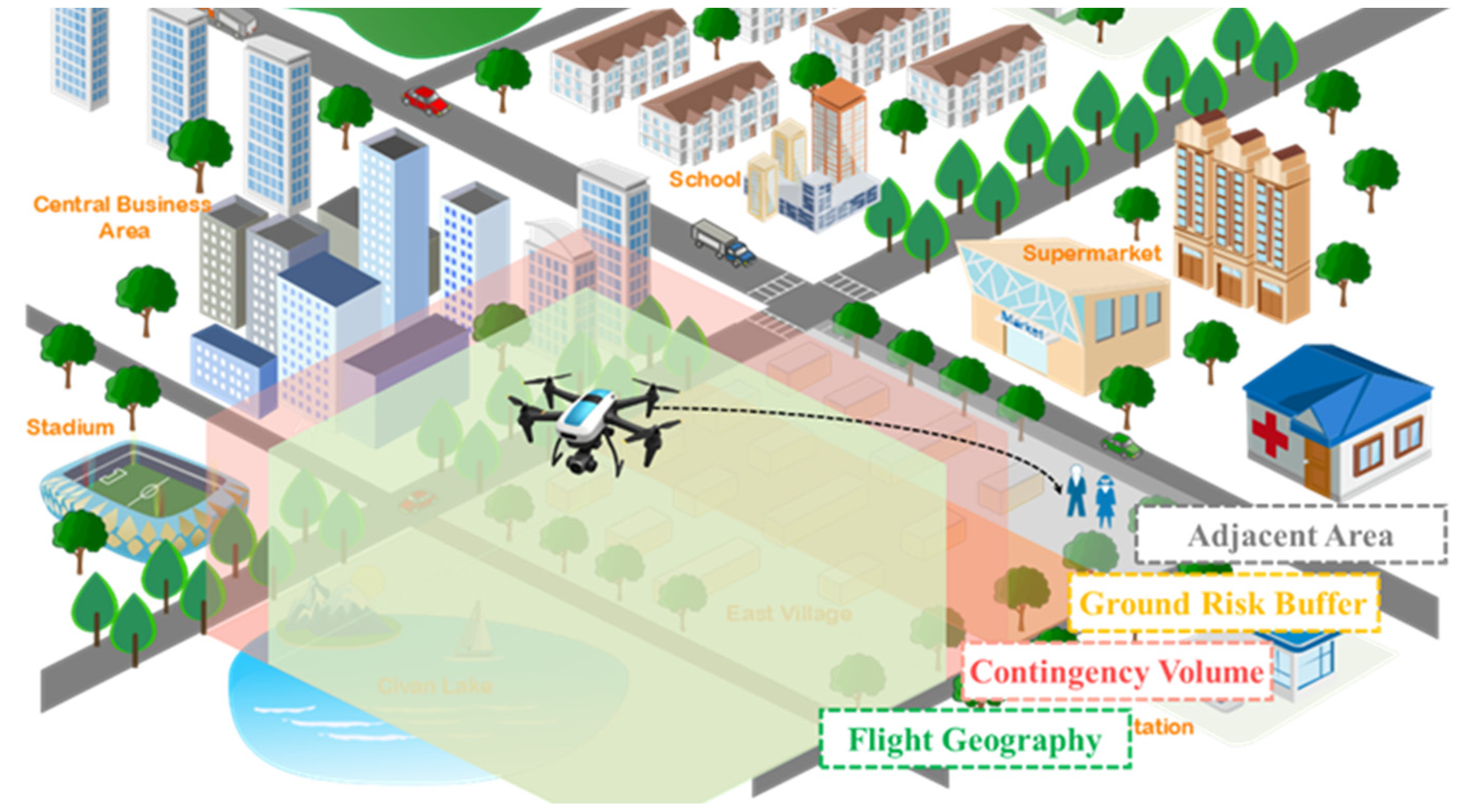
2. Problem Description
3. Derivation of Ground Risk Factors
3.1. Intrinsic UAV Ground Risk Matrix
3.2. Ground Risk Mitigation Effects
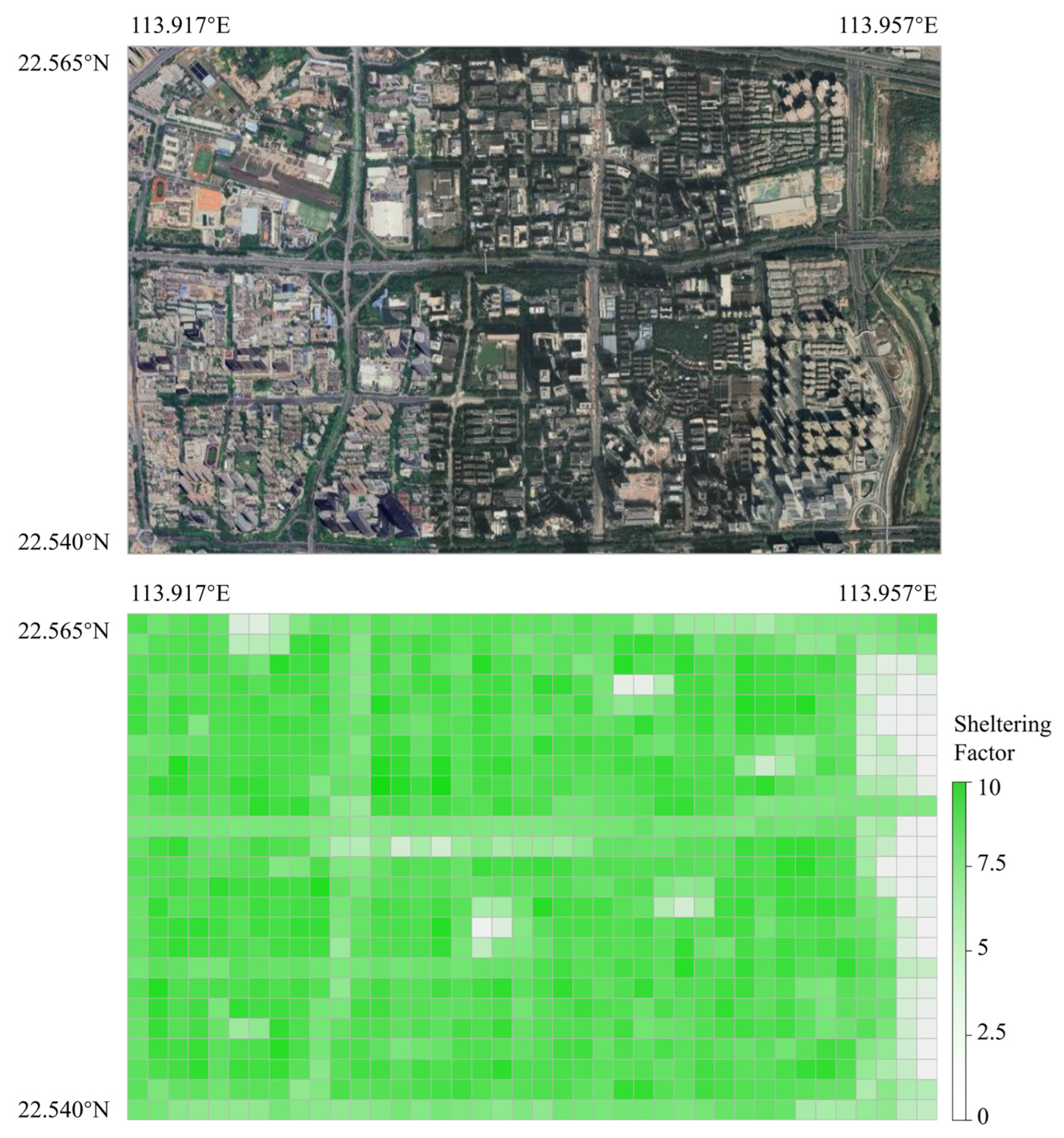
3.2.1. Ground Sheltering Effects
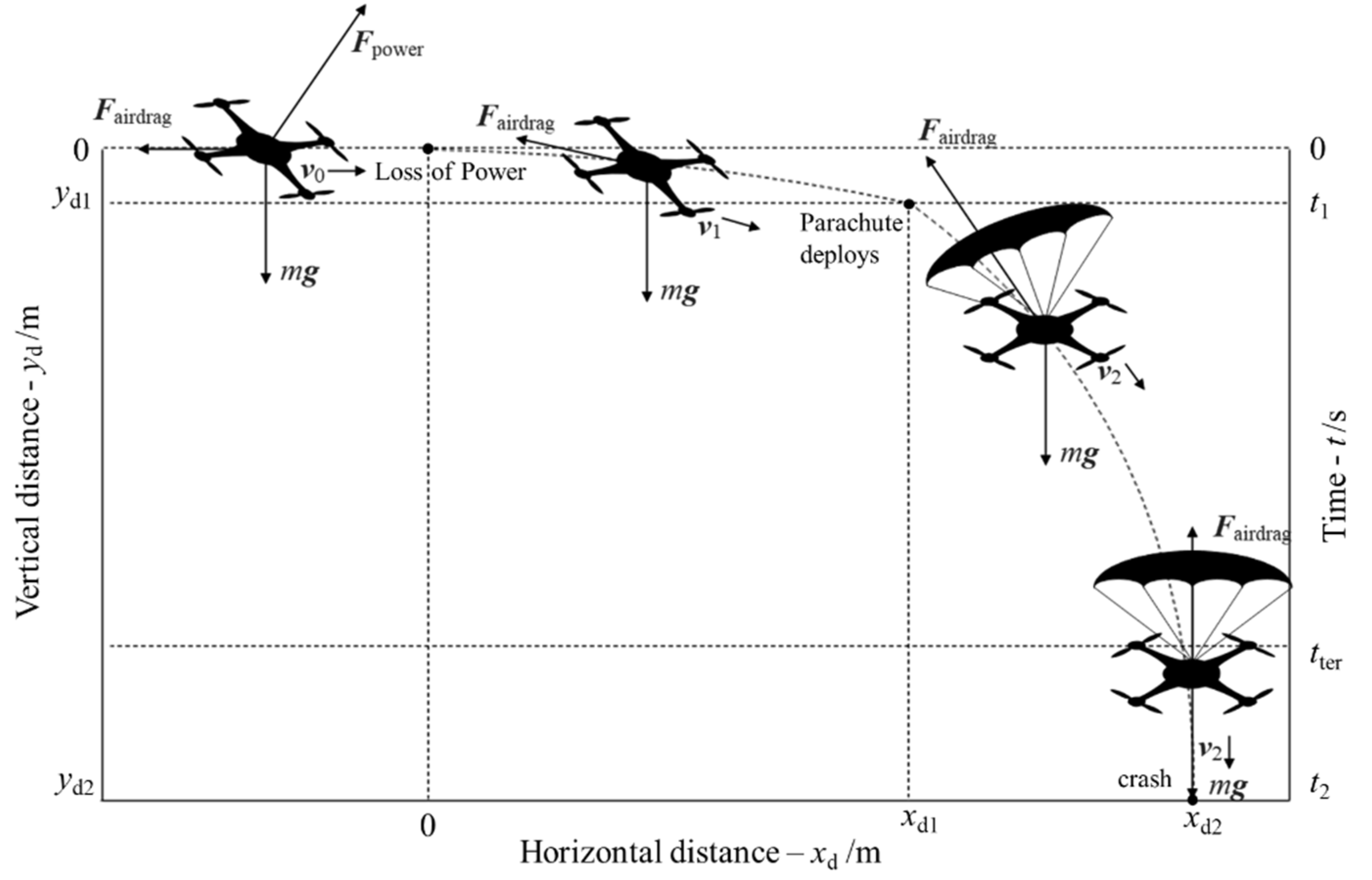
3.2.2. Parachute Systems
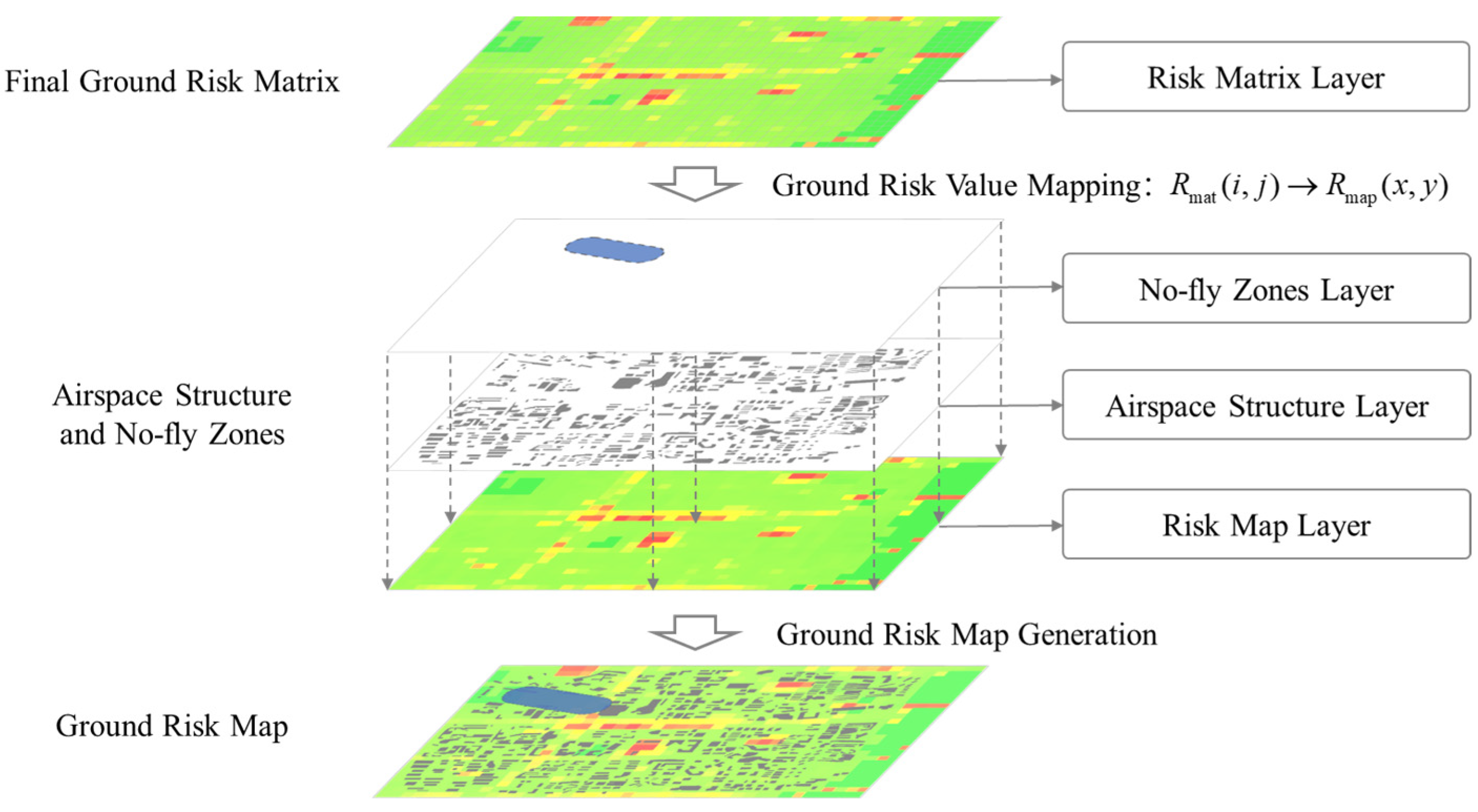
4. Generation of Ground Risk Map
4.1. Final UAV Ground Risk Matrix
- When , i.e., , and according to Equation (10), the intrinsic ground risk .
- When , i.e., , meaning the expected casualties of the parachute descent .
- When , Equation (32) can be defined,
4.2. Ground Risk Map
5. Experiments and Discussions
5.1. Simulation Scenario and Parameter Settings
5.1.1. Simulation Scenario, Datasets, and Parameter Settings
5.1.2. UAV Parameter Settings
5.2. Case Study and Analyses
5.2.1. Results of Ground Risk Map Generation
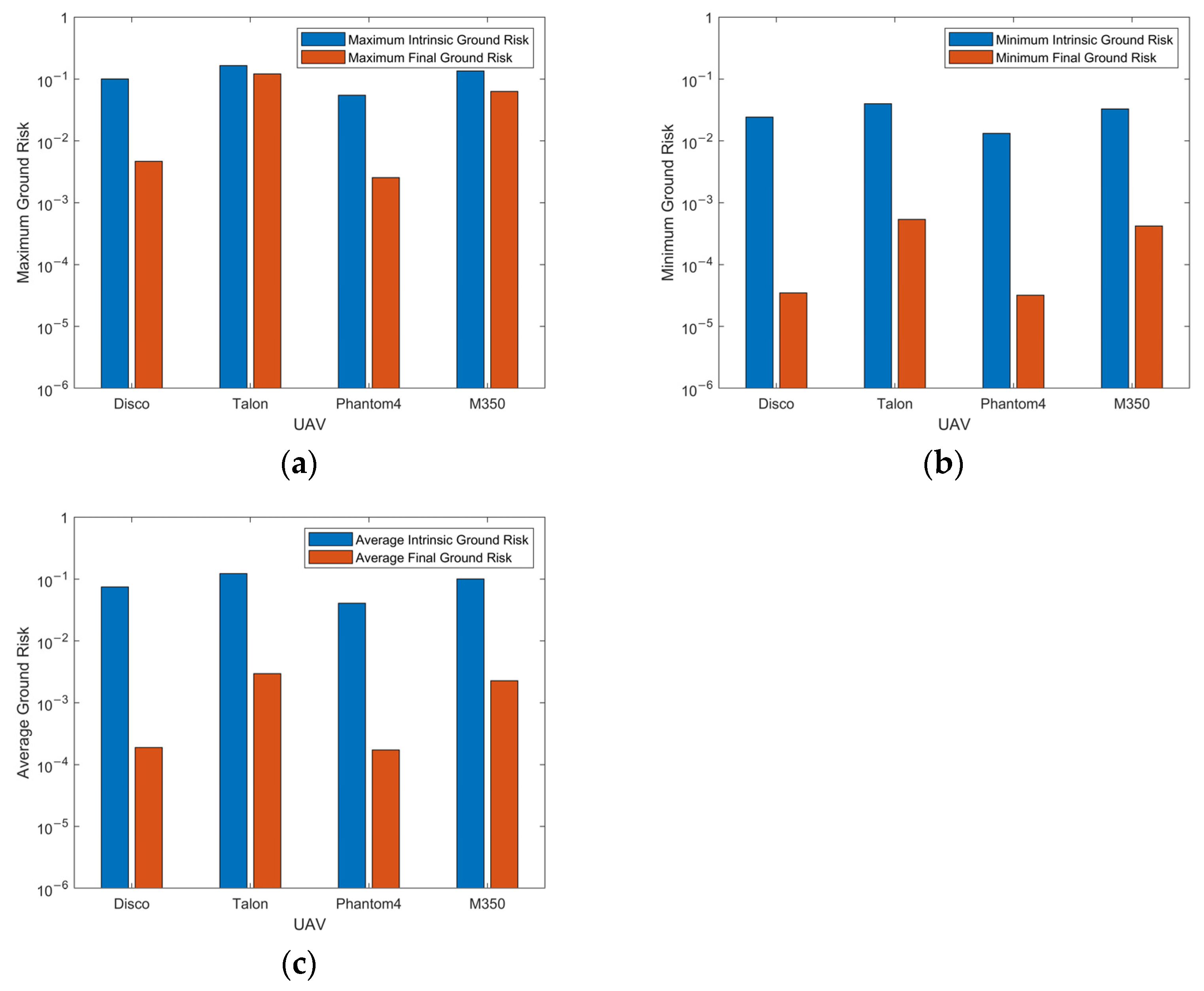
5.2.2. The Influence of UAV Parameters
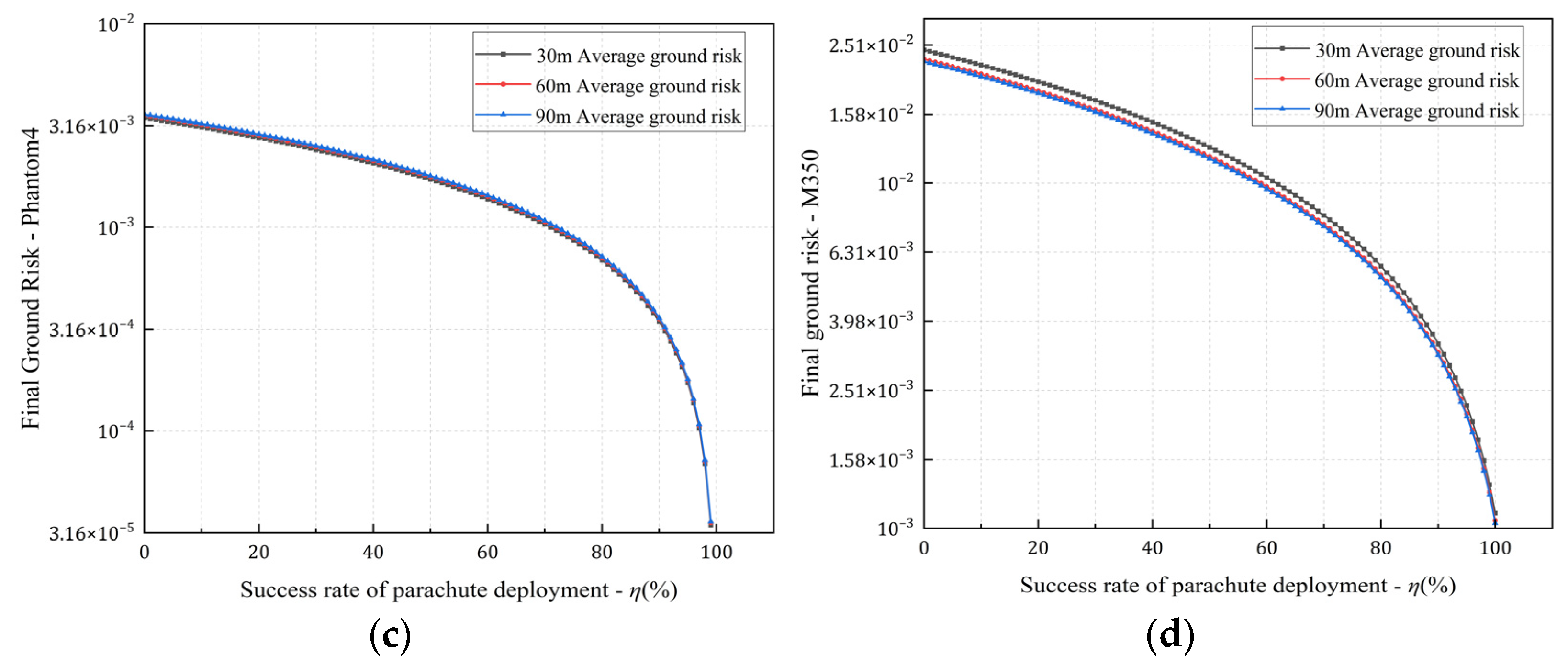
5.2.3. The Influence of UAV Flight Altitude on Risk Mitigations
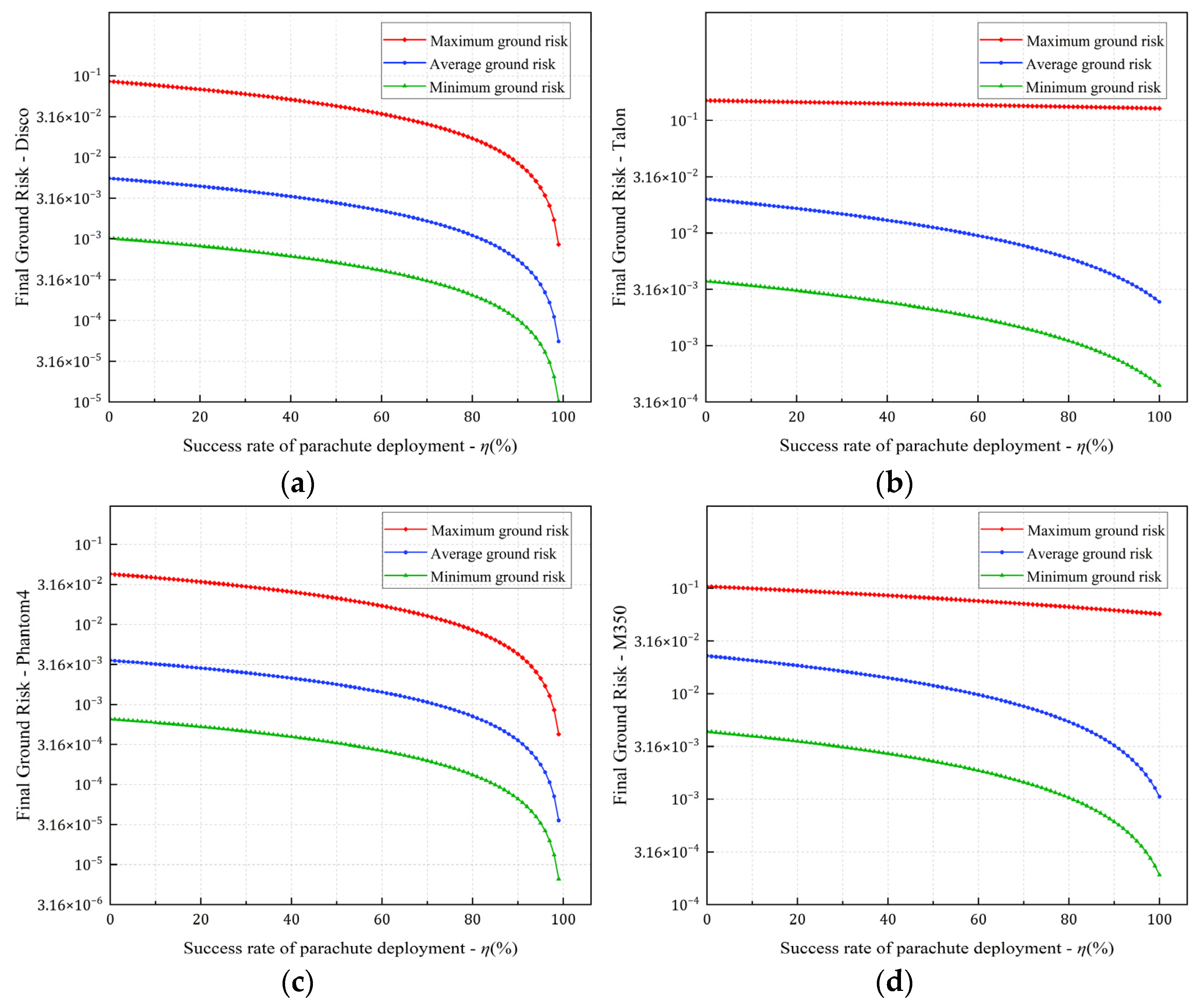
5.2.4. The Influence of Parachute Deployment Success Rate
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FAA. Urban Air Mobility (UAM) Concept of Operations v2.0; Federal Aviation Administration: Washington, DC, USA, 2023. [Google Scholar]
- Holden, J.; Goel, N. Fast-Forwarding to a Future of on-Demand Urban Air Transportation; UBER: San Francisco, CA, USA, 2016. [Google Scholar]
- McFarland, M. Amazon Gets Closer to Drone Delivery with FAA Approval|CNN Business. Available online: https://www.cnn.com/2020/08/31/tech/amazon-drone-faa-approval/index.html (accessed on 11 July 2024).
- Meituan. Meituan Unveils Self-Developed Drone Model, Plans for Drone Logistics Network at 2021 World Artificial Intelligence Conference. Available online: https://www.prnewswire.com/news-releases/meituan-unveils-self-developed-drone-model-plans-for-drone-logistics-network-at-2021-world-artificial-intelligence-conference-301327951.html (accessed on 11 July 2024).
- CAAC. CAAC Issues the First License for the Trial Operation of UAS in Urban Areas. Available online: http://www.caac.gov.cn/XWZX/MHYW/201910/t20191021_199030.html (accessed on 11 July 2024).
- JARUS. JARUS Guidelines on Specific Operations Risk Assessment (SORA), Main Body Release v2.5; Joint Authorities for Rulemaking of Unmanned Systems: Vienna, Austria, 2024. [Google Scholar]
- Zheng, Q.; Zhao, P.; Zhang, D.; Wang, H. MR-DCAE: Manifold Regularization-based Deep Convolutional Autoencoder for Unauthorized Broadcasting Identification. Int. J. Intell. Syst. 2021, 36, 7204–7238. [Google Scholar] [CrossRef]
- ALSA CENTER. Multi-Service Tactics, Techniques, And Procedures For Kill Box Employment; AIR LAND SEA APPLICATION CENTER: Hampton, VA, USA, 2009. [Google Scholar]
- Zhang, X.; Liu, Y.; Zhang, Y.; Guan, X.; Delahaye, D.; Tang, L. Safety Assessment and Risk Estimation for Unmanned Aerial Vehicles Operating in National Airspace System. J. Adv. Transp. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Hu, X.; Pang, B.; Dai, F.; Low, K.H. Risk Assessment Model for UAV Cost-Effective Path Planning in Urban Environments. IEEE Access 2020, 8, 150162–150173. [Google Scholar] [CrossRef]
- Li, R.; Shao, Q.; Dong, M. Path Planning for UAV in Urban Air Mobility Based on Risk Management. Aeronaut. Comput. Tech. 2021, 51, 73–77. [Google Scholar]
- Han, P.; Yang, X.; Zhao, Y.; Guan, X.; Wang, S. Quantitative Ground Risk Assessment for Urban Logistical Unmanned Aerial Vehicle (UAV) Based on Bayesian Network. Sustainability 2022, 14, 5733. [Google Scholar] [CrossRef]
- Han, P.; Zhang, B. Effect of track error on safety risk assessment of UAV ground impact. China Saf. Sci. J. 2021, 31, 106–111. [Google Scholar]
- Zhang, Z.; Zhang, S.; Liu, X.; Jin, L. Estimated method of target level of safety for unmanned aircraft system. J. Aerosp. Power 2018, 33, 1017–1024. [Google Scholar]
- Bu, J.; Zhang, H.; Hu, M.; Liu, H. Risk assessment of unmanned aerial vehicle flight based on K-means clustering algorithm. Trans. Nanjing Univ. Aeronaut. Astronaut. 2020, 37, 263–273. [Google Scholar]
- Cour-Harbo, A. la Ground Impact Probability Distribution for Small Unmanned Aircraft in Ballistic Descent. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; IEEE: Athens, Greece, 2020; pp. 1442–1451. [Google Scholar]
- Cour-Harbo, A. Quantifying Risk of Ground Impact Fatalities for Small Unmanned Aircraft. J. Intell. Robot. Syst. 2019, 93, 367–384. [Google Scholar] [CrossRef]
- Du, S.; Zhong, G.; Wang, F.; Pang, B.; Zhang, H.; Jiao, Q. Safety Risk Modelling and Assessment of Civil Unmanned Aircraft System Operations: A Comprehensive Review. Drones 2024, 8, 354. [Google Scholar] [CrossRef]
- Primatesta, S.; Capello, E.; Antonini, R.; Gaspardone, M.; Guglieri, G.; Rizzo, A. A Cloud-Based Framework for Risk-Aware Intelligent Navigation in Urban Environments. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; IEEE: Miami, FL, USA, 2017; pp. 447–455. [Google Scholar]
- Primatesta, S.; Cuomo, L.S.; Guglieri, G.; Rizzo, A. An Innovative Algorithm to Estimate Risk Optimum Path for Unmanned Aerial Vehicles in Urban Environments. Transp. Res. Procedia 2018, 35, 44–53. [Google Scholar] [CrossRef]
- Primatesta, S.; Guglieri, G.; Rizzo, A. A Risk-Aware Path Planning Strategy for UAVs in Urban Environments. J. Intell. Robot. Syst. 2019, 95, 629–643. [Google Scholar] [CrossRef]
- Primatesta, S.; Rizzo, A.; La Cour-Harbo, A. Ground Risk Map for Unmanned Aircraft in Urban Environments. J. Intell. Robot. Syst. 2020, 97, 489–509. [Google Scholar] [CrossRef]
- Li, Q.; Wu, Q.; Tu, H.; Zhang, J.; Zou, X.; Huang, S. Ground Risk Assessment for Unmanned Aircraft Focusing on Multiple Risk Sources in Urban Environments. Processes 2023, 11, 542. [Google Scholar] [CrossRef]
- Pang, B.; Hu, X.; Dai, W.; Low, K.H. UAV Path Optimization with an Integrated Cost Assessment Model Considering Third-Party Risks in Metropolitan Environments. Reliab. Eng. Syst. Saf. 2022, 222, 108399. [Google Scholar] [CrossRef]
- Pilko, A.; Sóbester, A.; Scanlan, J.P.; Ferraro, M. Spatiotemporal Ground Risk Mapping for Uncrewed Aerial Systems Operations. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3 January 2022; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2022. [Google Scholar]
- Jiao, Q.; Liu, Y.; Zheng, Z.; Sun, L.; Bai, Y.; Zhang, Z.; Sun, L.; Ren, G.; Zhou, G.; Chen, X.; et al. Ground Risk Assessment for Unmanned Aircraft Systems Based on Dynamic Model. Drones 2022, 6, 324. [Google Scholar] [CrossRef]
- Pang, B.; Hu, X.; Poh, Y.Y.; Low, K.H. Population Density Estimation for Dynamic Ground Risk Assessment of Drone Operations. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1 October 2023; IEEE: Barcelona, Spain, 2023; pp. 1–6. [Google Scholar]
- Ye, M.; Zhao, J.; Guan, Q.; Zhang, X. Research on eVTOL Air Route Network Planning Based on Improved A* Algorithm. Sustainability 2024, 16, 561. [Google Scholar] [CrossRef]
- Zhang, H.; Gan, X.; Li, S.; Chen, Z. UAV Safe Route Planning Based on PSO-BAS Algorithm. J. Syst. Eng. Electron. 2022, 33, 1151–1160. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Gao, Z.; Ren, J.; Zhou, S.; Yang, B. A Ground-Risk-Map-Based Path-Planning Algorithm for UAVs in an Urban Environment with Beetle Swarm Optimization. Appl. Sci. 2023, 13, 11305. [Google Scholar] [CrossRef]
- Pang, B.; Low, K.H.; Lv, C. Adaptive Conflict Resolution for Multi-UAV 4D Routes Optimization Using Stochastic Fractal Search Algorithm. Transp. Res. Part C Emerg. Technol. 2022, 139, 103666. [Google Scholar] [CrossRef]
- JARUS. JARUS Guidelines on Specific Operations Risk Assessment (SORA), Annex F Release v2.5; Joint Authorities for Rulemaking of Unmanned Systems: Vienna, Austria, 2024. [Google Scholar]
- JARUS. JARUS Guidelines on Specific Operations Risk Assessment (SORA), Annex B Release v2.5; Joint Authorities for Rulemaking of Unmanned Systems: Vienna, Austria, 2024. [Google Scholar]
- Bai, C.; Guo, Y.; Liu, X. Research progress of collision safety characteristics of civil light and small UAVs. Acta Aeronaut. et Astronaut. Sin. 2022, 43, 526832. [Google Scholar]
- Dalamagkidis, K.; Valavanis, K.P.; Piegl, L.A. On Integrating Unmanned Aircraft Systems into the National Airspace System: Issues, Challenges, Operational Restrictions, Certification, and Recommendations; Springer: Dordrecht, The Netherlands, 2012; ISBN 978-94-007-2478-5. [Google Scholar]
- Wilde, P. Common Risk Criteria Standards for National Test Ranges; Technical Report; Range Commanders Council: White Sands Missile Range, NM, USA, 2020. [Google Scholar]
- Guglieri, G.; Quagliotti, F.; Ristorto, G. Operational Issues and Assessment of Risk for Light UAVs. J. Unmanned Veh. Syst. 2014, 2, 119–129. [Google Scholar] [CrossRef]
- JARUS. JARUS Guidelines on Specific Operations Risk Assessment (SORA), Explanatory Note Release v2.5; Joint Authorities for Rulemaking of Unmanned Systems: Vienna, Austria, 2024. [Google Scholar]
- Google Map. Available online: https://www.google.com/maps/place/%E4%B8%AD%E5%9B%BD%E5%B9%BF%E4%B8%9C%E7%9C%81%E6%B7%B1%E5%9C%B3%E5%B8%82/@22.5458323,113.942107,6752m/data=!3m1!1e3!4m6!3m5!1s0x3403f408d0e15291:0xfdee550db79280c9!8m2!3d22.5428599!4d114.05956!16zL20vMGxibXY?hl=zh-cn&entry=ttu&g_ep=EgoyMDI0MTAyOS4wIKXMDSoASAFQAw%3D%3D (accessed on 2 November 2024).
- OpenStreetMap. Available online: https://www.openstreetmap.org/#map=15/22.54760/113.93187&layers=P (accessed on 2 November 2024).
- WorldPop. Population Counts/Constrained Individual Countries 2020 (100 m Resolution). Available online: https://hub.worldpop.org/geodata/listing?id=78 (accessed on 14 October 2024).
- Flyfire. UAV Parachute Systems. Available online: https://www.xflyfire.com/h-col-266.html (accessed on 7 August 2024).






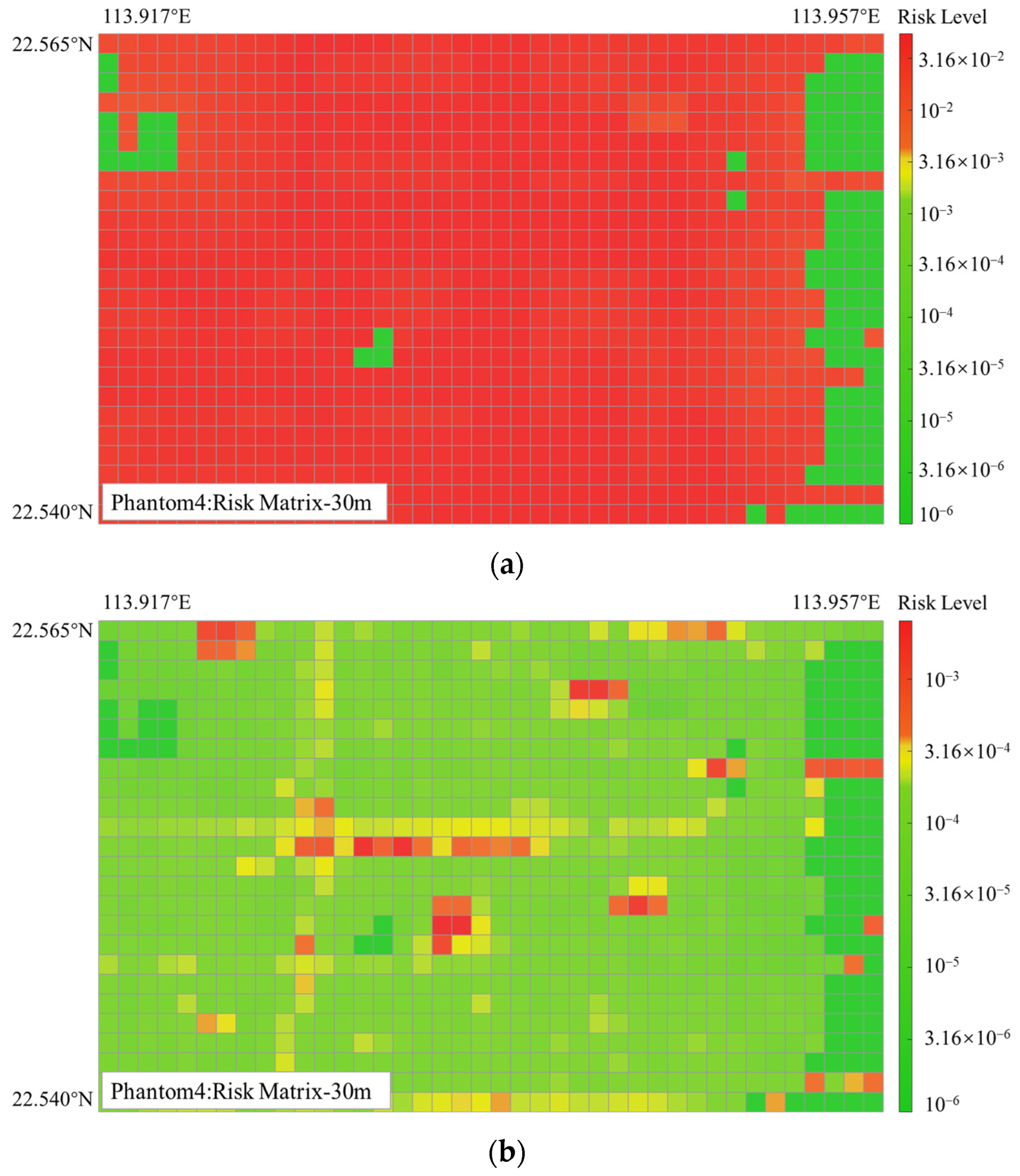

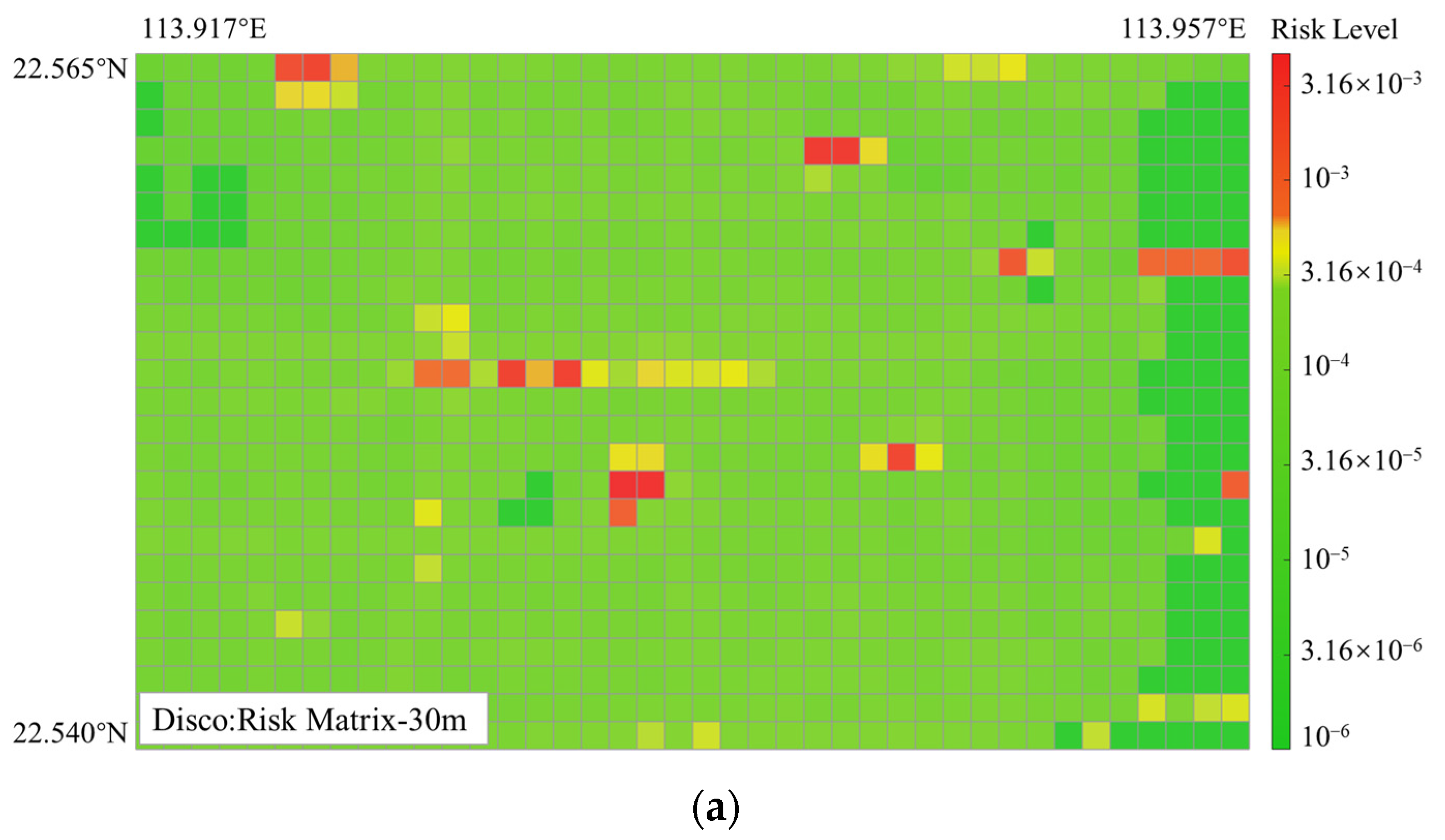
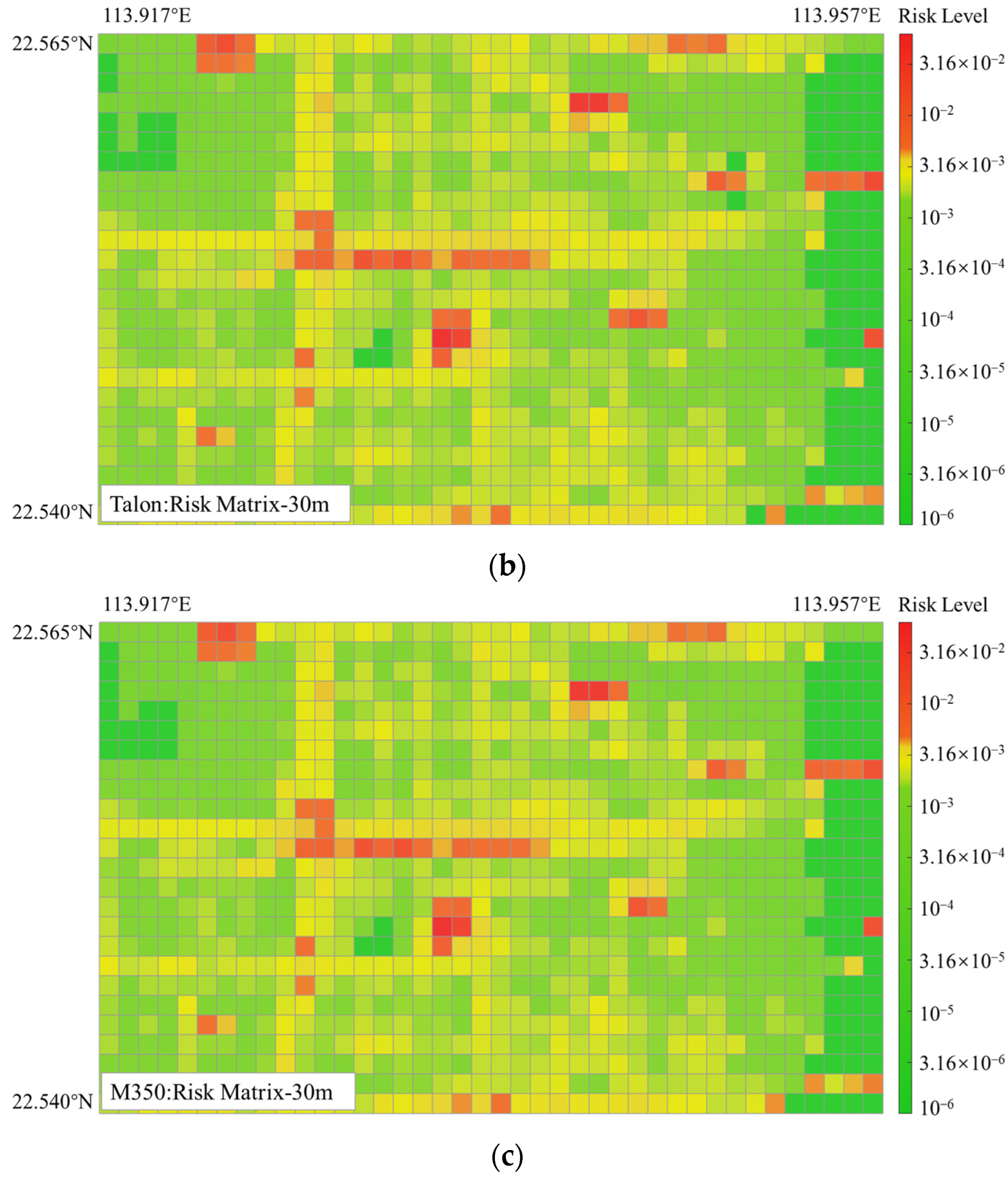


| Type | Ground Characteristics | Sheltering |
|---|---|---|
| Type 1 | Complete sheltering, e.g., industrial buildings | 10 |
| Type 2 | Strong sheltering, e.g., forest parks and low buildings | 7.5 |
| Type 3 | Moderate level sheltering, e.g., vehicles | 5 |
| Type 4 | Slight sheltering, e.g., sparse trees and street furniture | 2.5 |
| Type 5 | No sheltering, e.g., wetlands and grass | 0 |
| Parameters | Value |
|---|---|
| Gravitational acceleration (m/s2) | 9.8 |
| Air density (kg/m3) | 1.225 |
| Human average height (m) | 1.8 |
| Human average radius (m) | 0.3 |
| Operating altitude (m) | 30/60/90 |
| (J) | 3.4 × 104 |
| (J) | 34 |
| Parachute system success rate | 95% |
| Parrot Disco | Talon | DJI Phantom4 | DJI M350 | |
|---|---|---|---|---|
| Type | Fixed wing | Fixed wing | Quadrotor | Quadrotor |
| Mass (kg) | 0.75 | 3.75 | 1.39 | 9.2 |
| Radius (m) | 0.575 | 0.88 | 0.18 | 0.45 |
| Cruising speed (m/s) | N(15, 2.5) | N(18, 2.5) | N(15, 0.2) | N(23, 0.2) |
| Front area (m2) | 0.07 | 0.1 | 0.02 | 0.046 |
| Drag coefficient of UAVs | N(0.9, 0.2) | N(0.9, 0.2) | N(0.8, 0.2) | N(0.8, 0.2) |
| Parachute area (m2) | 0.5 | 1 | 1.1 | 7.3 |
| Drag coefficient of parachute | N(1.3, 0.2) | N(1.3, 0.2) | N(1.1, 0.2) | N(1.1, 0.2) |
| Parachute deployment time (s) | 1.2 | 1.2 | 0.7 | 0.7 |
| UAV | 30 m | 60 m | 90 m | |
|---|---|---|---|---|
| Parrot Disco | Maximum | 4.680 × 10−3 | 4.273 × 10−3 | 4.112 × 10−3 |
| Minimum | 3.480 × 10−5 | 5.118 × 10−5 | 6.238 × 10−5 | |
| Average | 1.895 × 10−4 | 2.766 × 10−4 | 3.361 × 10−4 | |
| Talon | Maximum | 1.213 × 10−1 | 1.290 × 10−1 | 1.319 × 10−1 |
| Minimum | 5.395 × 10−4 | 6.094 × 10−4 | 6.518 × 10−4 | |
| Average | 2.957 × 10−3 | 3.331 × 10−3 | 3.553 × 10−3 | |
| DJI Phantom4 | Maximum | 2.549 × 10−3 | 2.130 × 10−3 | 1.956 × 10−3 |
| Minimum | 3.198 × 10−5 | 3.301 × 10−5 | 3.343 × 10−5 | |
| Average | 1.727 × 10−4 | 1.778 × 10−4 | 1.798 × 10−4 | |
| DJI M350 | Maximum | 6.307 × 10−2 | 5.942 × 10−2 | 5.812 × 10−2 |
| Minimum | 4.213 × 10−4 | 4.005 × 10−4 | 3.959 × 10−4 | |
| Average | 2.268 × 10−3 | 2.144 × 10−3 | 2.110 × 10−3 |
| UAV | 30 m | 90 m | |||
|---|---|---|---|---|---|
| Intrinsic Risk | Final Risk | Intrinsic Risk | Final Risk | ||
| Parrot Disco | Maximum | 1.008 × 10−1 | 4.680 × 10−3 | 8.861 × 10−2 | 4.112 × 10−3 |
| Minimum | 2.438 × 10−2 | 3.480 × 10−5 | 2.214 × 10−2 | 6.238 × 10−5 | |
| Average | 7.485 × 10−2 | 1.895 × 10−4 | 6.577 × 10−2 | 3.361 × 10−4 | |
| Talon | Maximum | 1.657 × 10−1 | 1.213 × 10−1 | 1.596 × 10−1 | 1.319 × 10−1 |
| Minimum | 4.006 × 10−2 | 5.395 × 10−4 | 3.858 × 10−2 | 6.518 × 10−4 | |
| Average | 1.230 × 10−1 | 2.957 × 10−3 | 1.185 × 10−1 | 3.553 × 10−3 | |
| DJI Phantom4 | Maximum | 5.494 × 10−2 | 2.549 × 10−3 | 4.214 × 10−2 | 1.956 × 10−3 |
| Minimum | 1.328 × 10−2 | 3.198 × 10−5 | 1.109 × 10−2 | 3.343 × 10−5 | |
| Average | 4.078 × 10−2 | 1.727 × 10−4 | 3.218 × 10−2 | 1.798 × 10−4 | |
| DJI M350 | Maximum | 1.359 × 10−1 | 6.307 × 10−2 | 1.023 × 10−1 | 5.812 × 10−2 |
| Minimum | 3.286 × 10−2 | 4.213 × 10−4 | 2.473 × 10−2 | 3.959 × 10−4 | |
| Average | 1.009 × 10−1 | 2.268 × 10−3 | 7.593 × 10−2 | 2.110 × 10−3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhang, X.; Li, Y.; Liu, Y.; Ma, J. Grid Matrix-Based Ground Risk Map Generation for Unmanned Aerial Vehicles in Urban Environments. Drones 2024, 8, 678. https://doi.org/10.3390/drones8110678
Zhu Y, Zhang X, Li Y, Liu Y, Ma J. Grid Matrix-Based Ground Risk Map Generation for Unmanned Aerial Vehicles in Urban Environments. Drones. 2024; 8(11):678. https://doi.org/10.3390/drones8110678
Chicago/Turabian StyleZhu, Yuanjun, Xuejun Zhang, Yan Li, Yang Liu, and Jianxiang Ma. 2024. "Grid Matrix-Based Ground Risk Map Generation for Unmanned Aerial Vehicles in Urban Environments" Drones 8, no. 11: 678. https://doi.org/10.3390/drones8110678
APA StyleZhu, Y., Zhang, X., Li, Y., Liu, Y., & Ma, J. (2024). Grid Matrix-Based Ground Risk Map Generation for Unmanned Aerial Vehicles in Urban Environments. Drones, 8(11), 678. https://doi.org/10.3390/drones8110678






