Modeling of the Flight Performance of a Plasma-Propelled Drone: Limitations and Prospects
Abstract
:1. Introduction
2. Modeling of the Propulsive Performance of Single-Stage EAD Thrusters
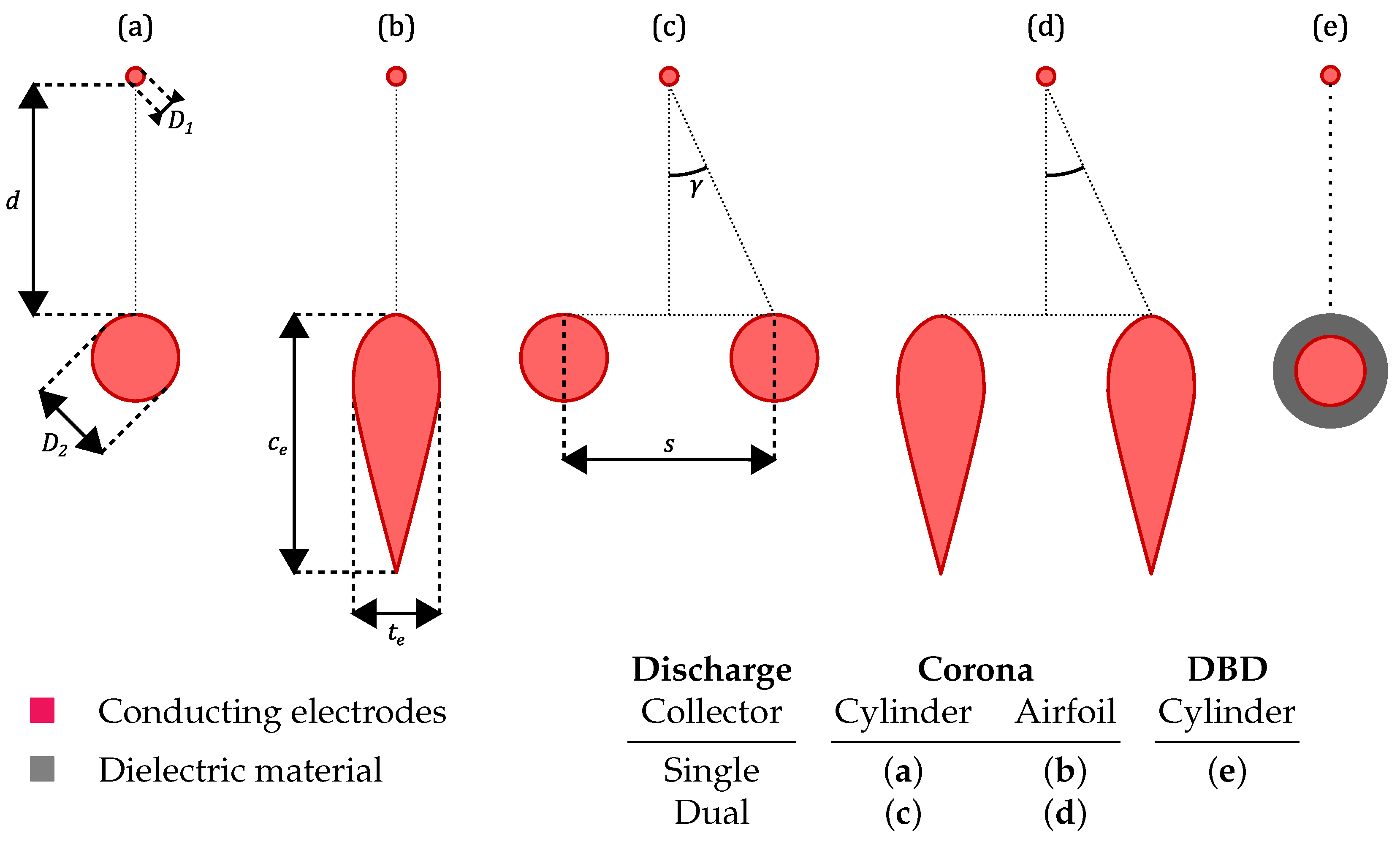
2.1. Different Types of Plasma Discharges
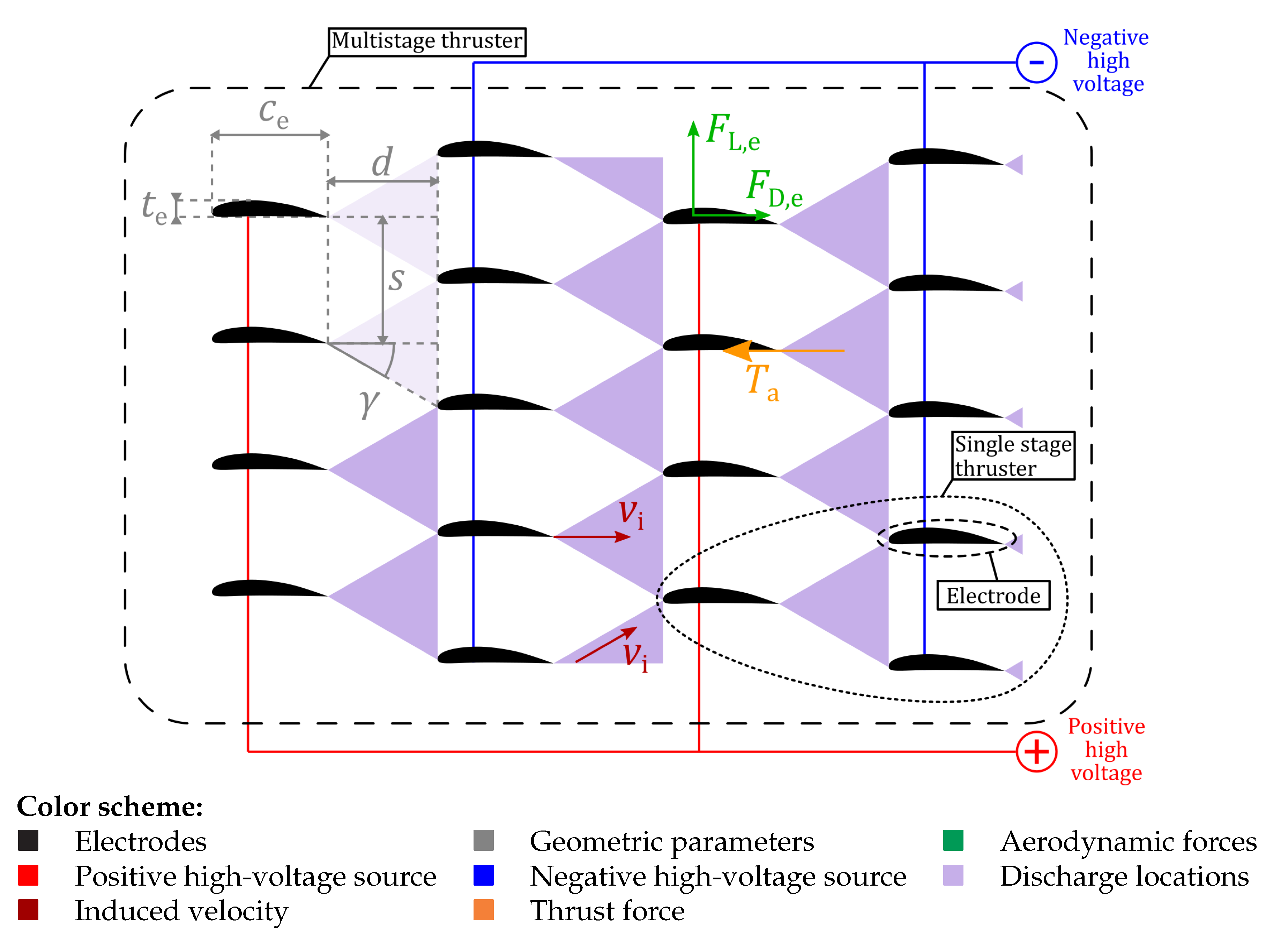
2.2. Physical Modeling of Single-Stage Thrusters
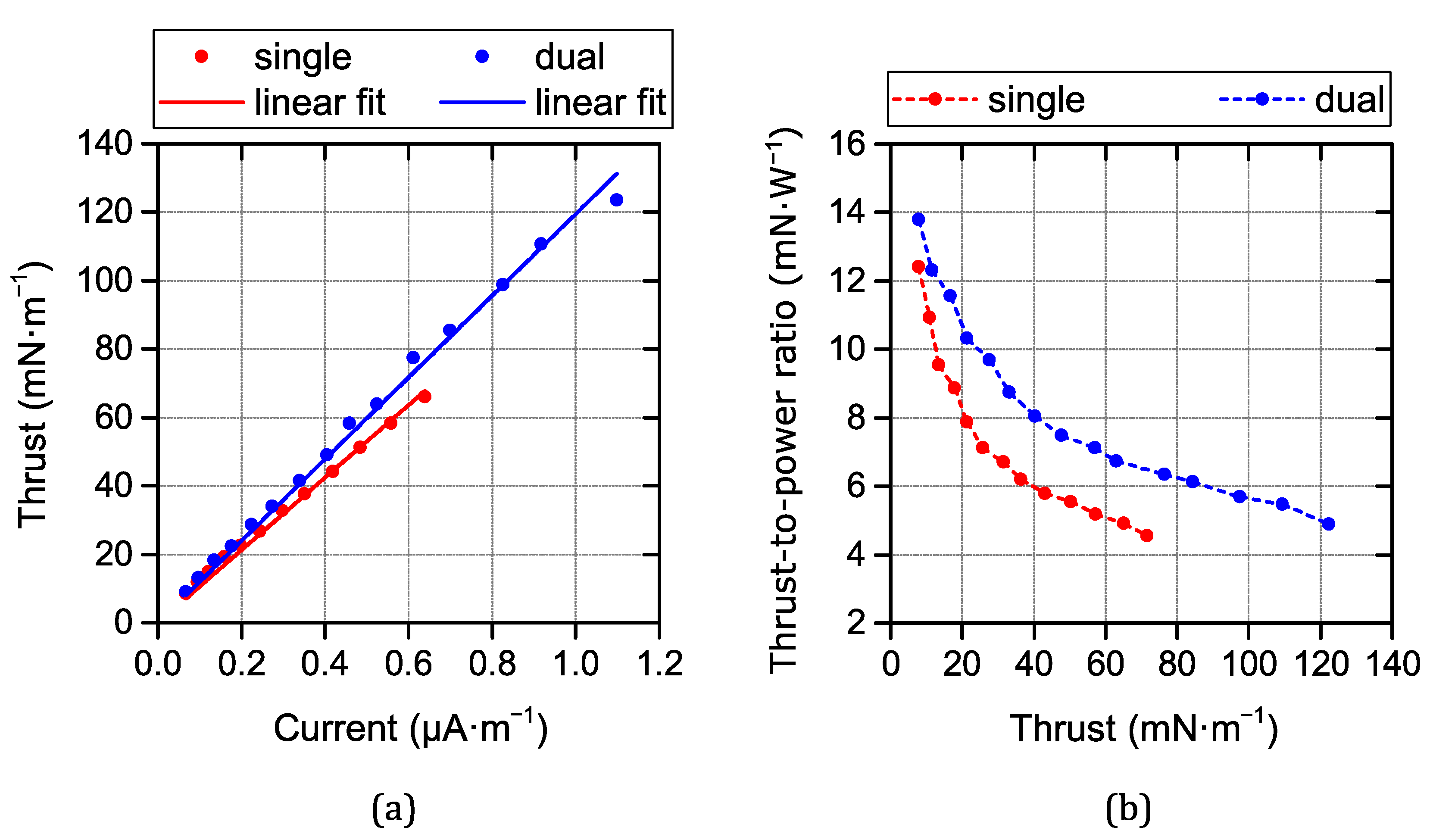
2.3. Current Performance of Single-Stage Thrusters and Prospects for Improvements
3. Propulsive Performance of a Multistage EAD Thruster in Flight
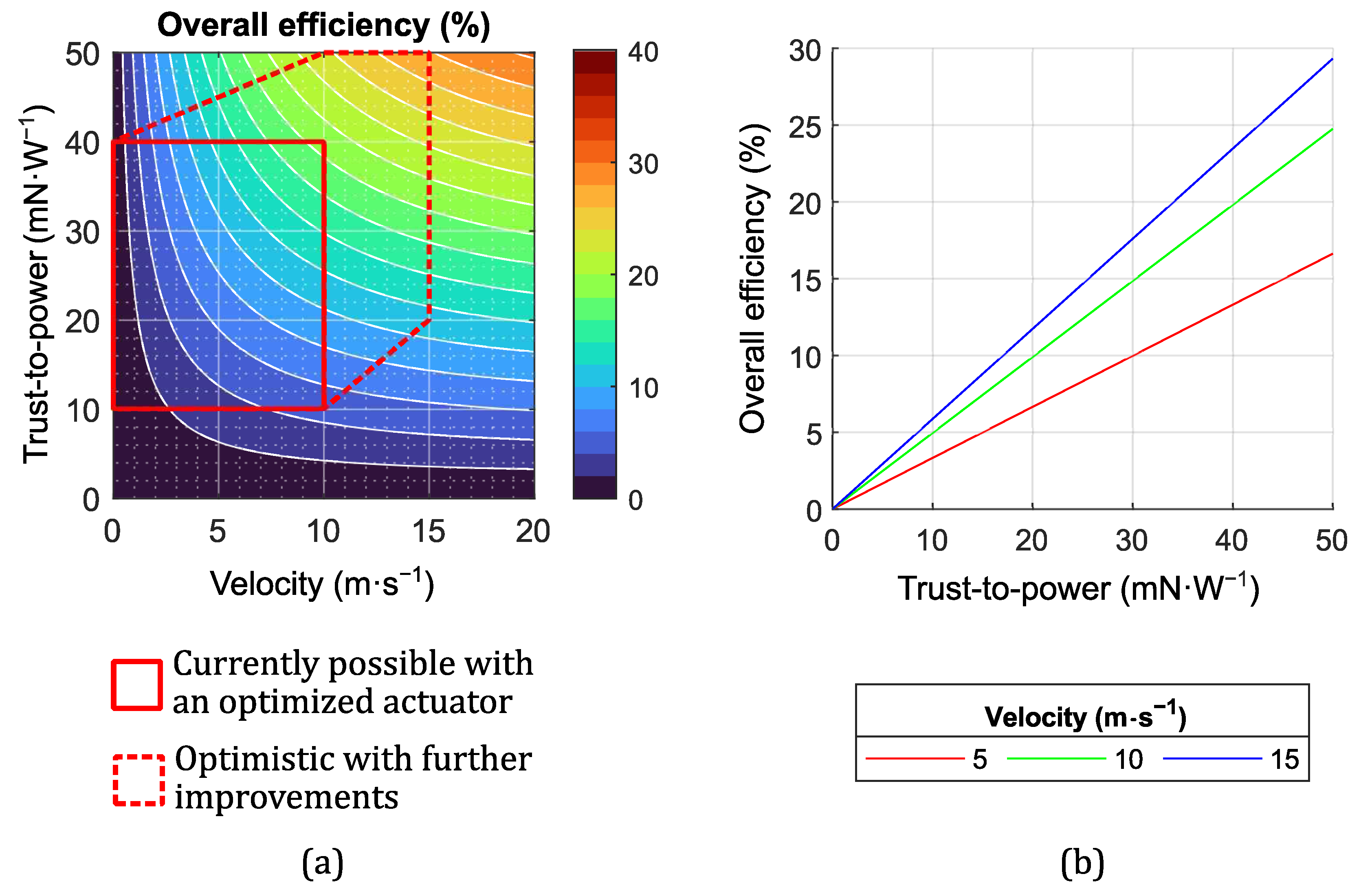
3.1. Available Thrust and Thrust-to-Power Ratio
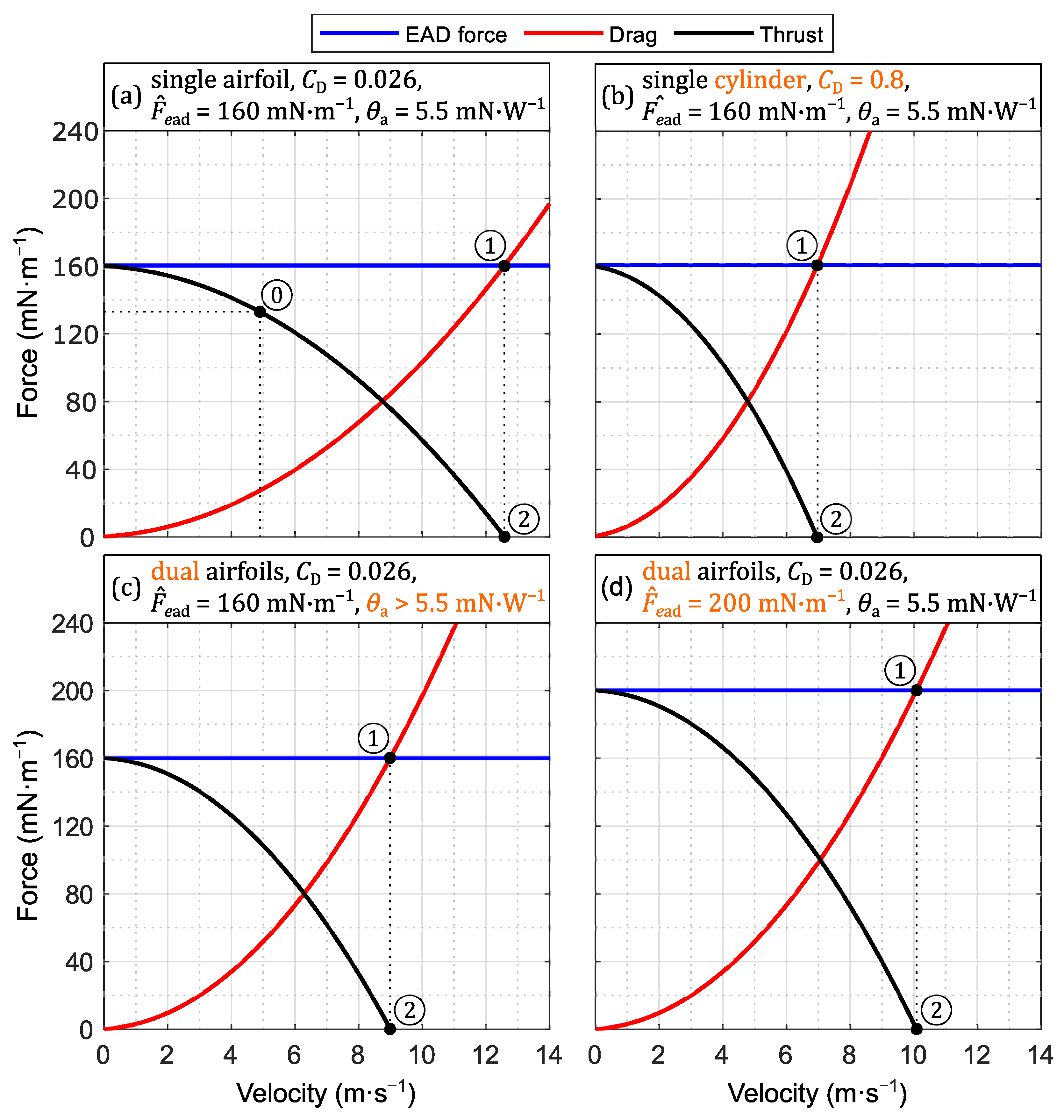
3.2. Achievable Flight Velocity
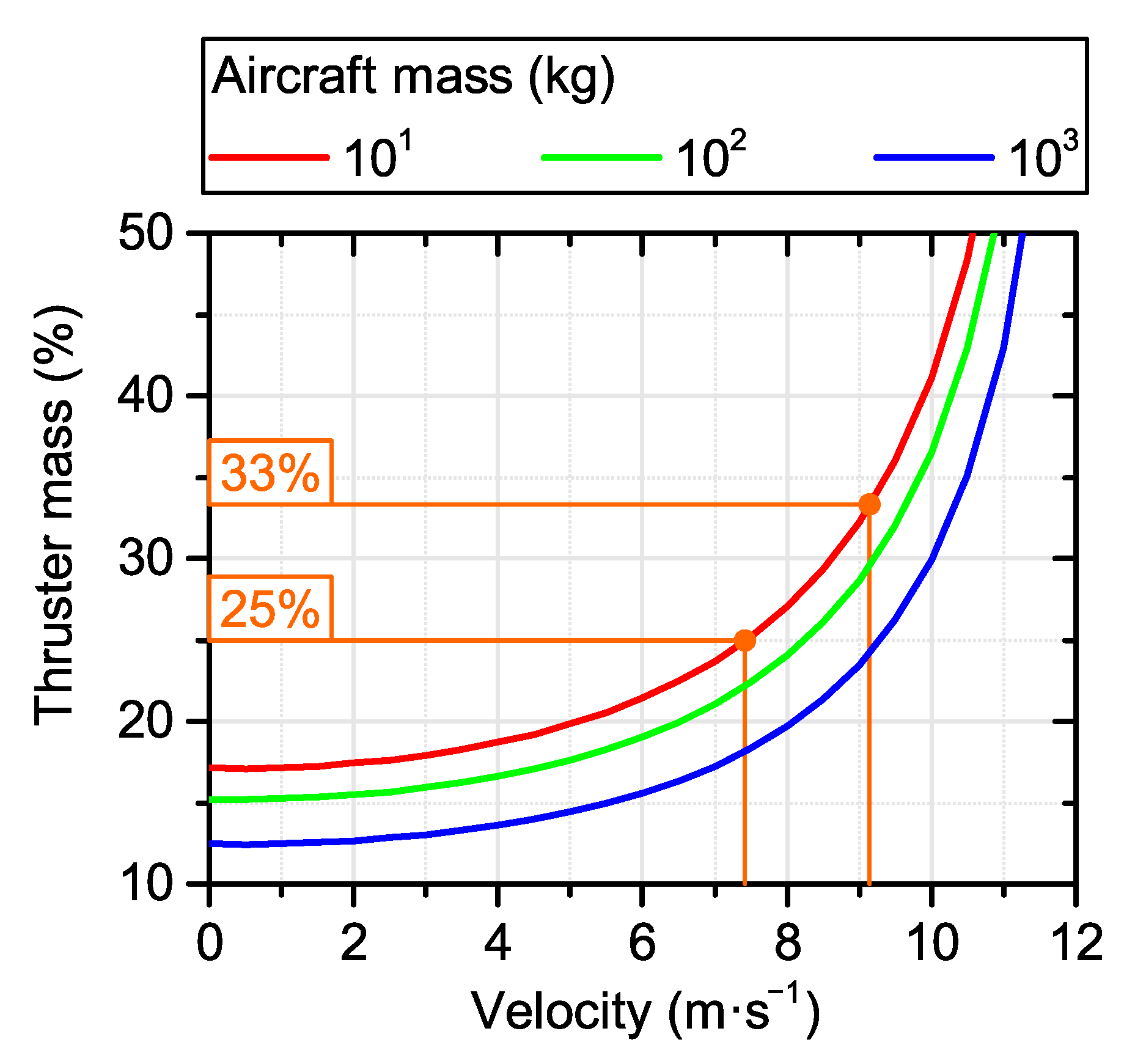
3.3. Thruster Design and Dimensions
4. Modeling of the Flight Performance of an EAD-Propelled Aircraft
4.1. Reference Flight Performance
4.2. Selected EAD Performance
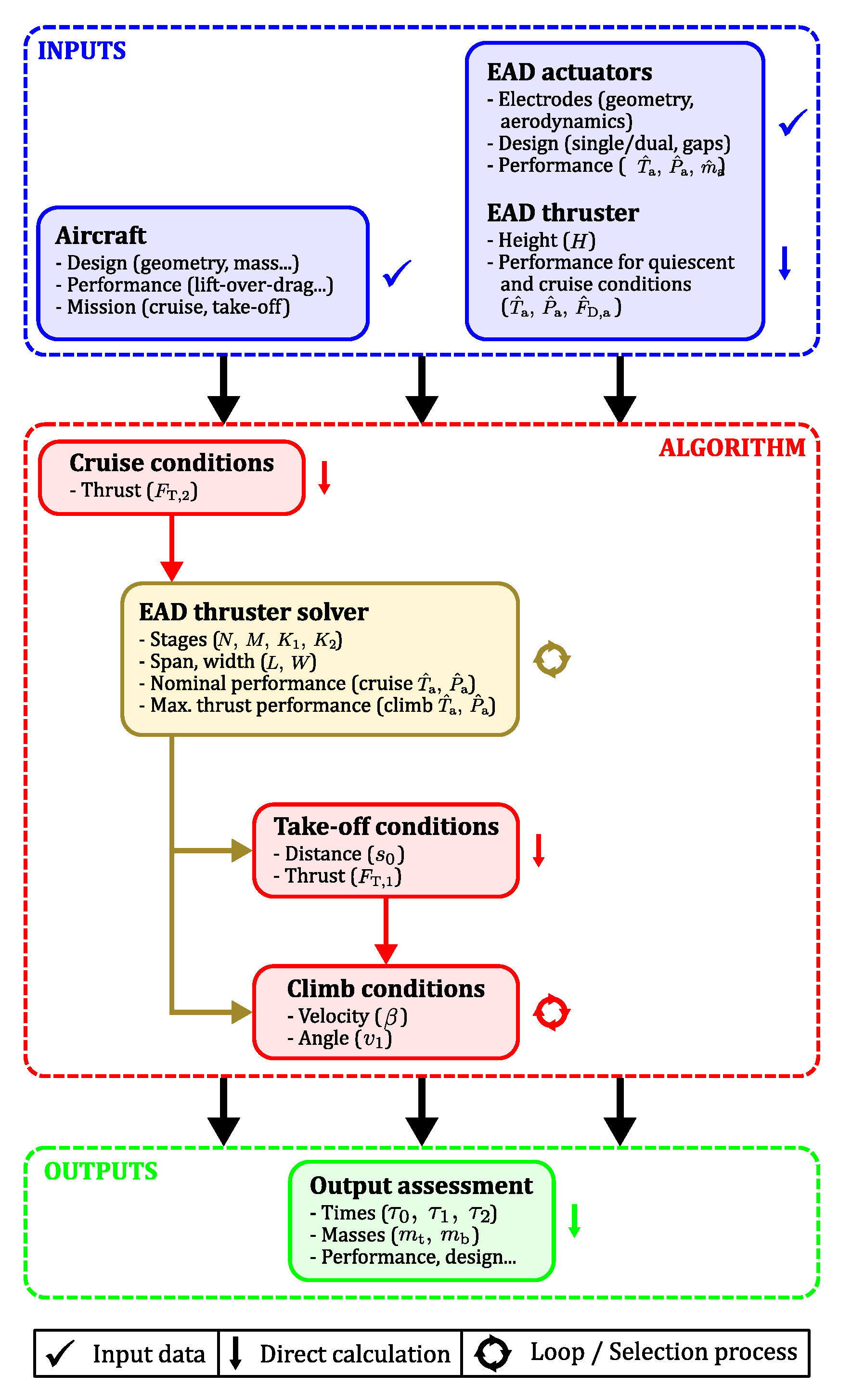
4.3. Solving Process
5. Results and Discussion
5.1. Reference EAD-Propelled Drone
5.2. Albatross UAV
5.3. Possible EAD-Propelled UAVs
5.4. The Participation of the Thruster in Lift Generation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| ANR | Agence National de Recherche |
| AR | Aspect ratio |
| DC | Direct current |
| EAD | Electro-aerodynamic |
| ISA | International Standard Atmosphere |
| MAV | Micro air vehicle |
| MTOW | Maximum takeoff weight |
| NACA | National Advisory Committee for Aeronautics |
| RC | Rate of climb |
| UAV | Unmanned aerial vehicle |
Appendix A. Applicability of Usual Thrust Equations

Appendix B. Aircraft Performance
Appendix B.1. Overall Design and Characteristics of the Aircraft
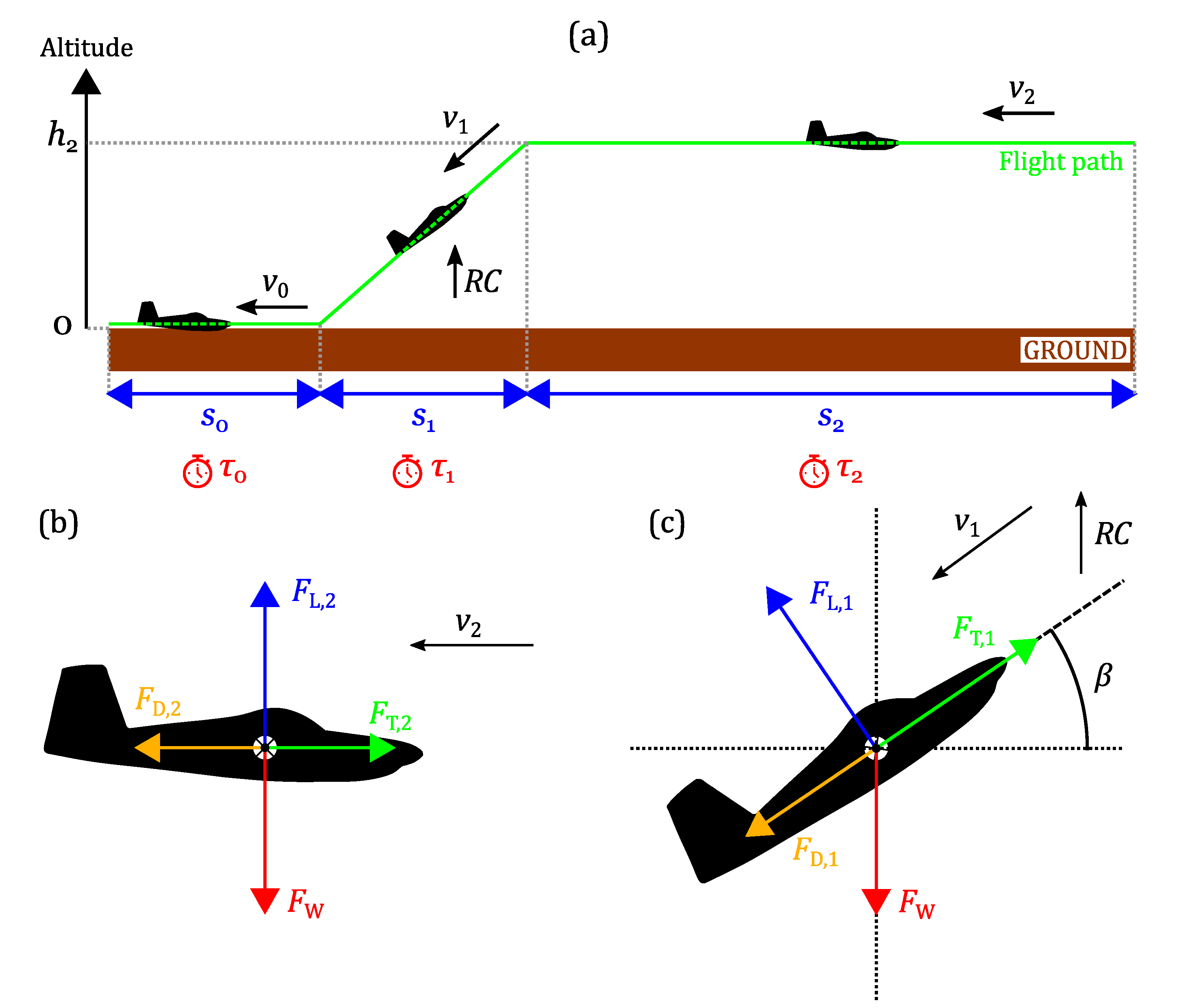

Appendix B.2. Cruise Flight
Appendix B.3. Steady Climb
Appendix B.4. Take-Off Performance
Appendix C. Process of the Algorithm
Appendix C.1. Input Data
Appendix C.2. Thruster Design and Cruise Performance
Appendix C.3. Take-Off and Climbing Performance
Appendix C.4. Output Parameters
References
- Xu, H.; He, Y.; Strobel, K.L.; Gilmore, C.K.; Kelley, S.P.; Hennick, C.C.; Sebastian, T.; Woolston, M.R.; Perreault, D.J.; Barrett, S.R.H. Flight of an aeroplane with solid-state propulsion. Nature 2018, 563, 532–535. [Google Scholar] [CrossRef]
- Poon, H.S.; Lam, M.K.K.; Chow, M.; Li, W.J. Noiseless and vibration-free Ionic Propulsion technology for indoor surveillance blimps. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2891–2896. [Google Scholar] [CrossRef]
- Drew, D.; Contreras, D.S.; Pister, K.S.J. First thrust from a microfabricated atmospheric ion engine. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NE, USA, 22–26 January 2017; pp. 346–349. [Google Scholar] [CrossRef]
- Drew, D.S.; Lambert, N.O.; Schindler, C.B.; Pister, K.S.J. Toward Controlled Flight of the Ionocraft: A Flying Microrobot Using Electrohydrodynamic Thrust With Onboard Sensing and No Moving Parts. IEEE Robot. Autom. Lett. 2018, 3, 2807–2813. [Google Scholar] [CrossRef]
- Moreau, E.; Benard, N.; Alicalapa, F.; Douyère, A. Electrohydrodynamic force produced by a corona discharge between a wire active electrode and several cylinder electrodes–Application to electric propulsion. J. Electrost. 2015, 76, 194–200. [Google Scholar] [CrossRef]
- Monrolin, N.; Plouraboué, F.; Praud, O. Electrohydrodynamic Thrust for In-Atmosphere Propulsion. AIAA J. 2017, 55, 4296–4305. [Google Scholar] [CrossRef]
- Monrolin, N.; Praud, O.; Plouraboué, F. Electrohydrodynamic ionic wind, force field, and ionic mobility in a positive dc wire-to-cylinders corona discharge in air. Phys. Rev. Fluids 2018, 3, 063701. [Google Scholar] [CrossRef]
- Dremin, D.V.; Khomich, V.Y.; Rebrov, I.E. Thrust and thrust-to-power ratio in electrohydrodynamic propulsion electrode systems. J. Physics Conf. Ser. 2017, 927, 012015. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L.; Orlov, D.M. SDBD plasma enhanced aerodynamics: Concepts, optimization and applications. Prog. Aerosp. Sci. 2007, 43, 193–217. [Google Scholar] [CrossRef]
- Corke, T.C.; Enloe, C.L.; Wilkinson, S.P. Dielectric Barrier Discharge Plasma Actuators for Flow Control. Annu. Rev. Fluid Mech. 2010, 42, 505–529. [Google Scholar] [CrossRef]
- Wang, J.J.; Choi, K.S.; Feng, L.H.; Jukes, T.N.; Whalley, R.D. Recent developments in DBD plasma flow control. Prog. Aerosp. Sci. 2013, 62, 52–78. [Google Scholar] [CrossRef]
- Xu, H.; He, Y.; Barrett, S.R.H. A dielectric barrier discharge ion source increases thrust and efficiency of electroaerodynamic propulsion. Appl. Phys. Lett. 2019, 114, 254105. [Google Scholar] [CrossRef]
- Bayoda, K.; Benard, N.; Moreau, E. Elongating the area of plasma/fluid interaction of surface nanosecond pulsed discharges. J. Electrost. 2015, 74, 79–84. [Google Scholar] [CrossRef]
- Moreau, E. Airflow control by non-thermal plasma actuators. J. Phys. Appl. Phys. 2007, 40, 605–636. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Chen, Y.; Ouyang, J. Characteristics of ionic wind in needle-to-ring corona discharge. J. Electrost. 2015, 74, 15–20. [Google Scholar] [CrossRef]
- Moreau, E.; Benard, N.; Lan-Sun-Luk, J.D.; Chabriat, J.P. Electrohydrodynamic force produced by a wire-to-cylinder dc corona discharge in air at atmospheric pressure. J. Phys. D Appl. Phys. 2013, 46, 475204. [Google Scholar] [CrossRef]
- Christenson, E.A.; Moller, P.S. Ion-neutral propulsion in atmospheric media. AIAA J. 1967, 5, 1768–1773. [Google Scholar] [CrossRef]
- Masuyama, K.; Barrett, S.R.H. On the performance of electrohydrodynamic propulsion. Proc. R. Soc. Math. Phys. Eng. Sci. 2013, 469, 20120623. [Google Scholar] [CrossRef]
- Kiousis, K.N.; Moronis, A.X.; Fruh, W.G. Electro-Hydrodynamic (EHD) Thrust Analysis in Wire-Cylinder Electrode Arrangement. Plasma Sci. Technol. 2014, 16, 363–369. [Google Scholar] [CrossRef]
- Stuetzer, O.M. Ion Drag Pressure Generation. J. Appl. Phys. 1959, 30, 984–994. [Google Scholar] [CrossRef]
- Gilmore, C.K.; Barrett, S.R.H. Electrohydrodynamic thrust density using positive corona-induced ionic winds for in-atmosphere propulsion. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 20140912. [Google Scholar] [CrossRef]
- Xu, H.; Gomez-Vega, N.; Agrawal, D.R.; Barrett, S.R.H. Higher thrust-to-power with large electrode gap spacing electroaerodynamic devices for aircraft propulsion. J. Phys. D Appl. Phys. 2020, 53, 025202. [Google Scholar] [CrossRef]
- Robinson, M. Movement of air in the electric wind of the corona discharge. Trans. Am. Inst. Electr. Eng. Part I Commun. Electron. 1961, 80, 143–150. [Google Scholar] [CrossRef]
- Chapman, S. Corona point current in wind. J. Geophys. Res. 1970, 75, 2165–2169. [Google Scholar] [CrossRef]
- Grosse, S.; Benard, N.; Moreau, E. Electroaerodynamic thrusters: Influence of a freestream on the current, ionic wind and force produced by a DC corona discharge. J. Electrost. 2024. submitted. [Google Scholar]
- Gilmore, C.K.; Barrett, S.R. Electroaerodynamic Thruster Performance as a Function of Altitude and Flight Speed. AIAA J. 2018, 56, 1105–1117. [Google Scholar] [CrossRef]
- Anderson, J.D. Elements of Airplane Performance. In Introduction to Flight, 8th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2016; pp. 441–588. [Google Scholar]
- Khomich, V.Y.; Rebrov, I.E. In-atmosphere electrohydrodynamic propulsion aircraft with wireless supply onboard. J. Electrost. 2018, 95, 1–12. [Google Scholar] [CrossRef]
- Martins, A.A.; Pinheiro, M.J. On the influence that the ground electrode diameter has in the propulsion efficiency of an asymmetric capacitor in nitrogen gas. Phys. Plasmas 2011, 18, 033512. [Google Scholar] [CrossRef]
- Khomich, V.; Malanichev, V.; Rebrov, I. Electrohydrodynamic thruster for near-space applications. Acta Astronaut. 2021, 180, 141–148. [Google Scholar] [CrossRef]
- Nelson, C.L.; Drew, D.S. High Aspect Ratio Multi-Stage Ducted Electroaerodynamic Thrusters for Micro Air Vehicle Propulsion. IEEE Robot. Autom. Lett. 2024, 9, 2702–2709. [Google Scholar] [CrossRef]
- Gomez-Vega, N.; Brown, A.; Xu, H.; Barrett, S.R.H. Model of Multistaged Ducted Thrusters for High-Thrust-Density Electroaerodynamic Propulsion. AIAA J. 2023, 61, 767–779. [Google Scholar] [CrossRef]
- Barrett, S.; Xu, H.; Brown, A.; Vega, N.G.; Perovich, N. Surface-Integrated Electroaerodynamic Thrusters. U.S. Patent US20230322368A1, 22 June 2023. [Google Scholar]
- Gomez-Vega, N.; Kambhampaty, J.D.; Barrett, S.R.H. Mitigating reverse emission in electroaerodynamic thrusters. J. Phys. D Appl. Phys. 2022, 55, 505202. [Google Scholar] [CrossRef]
- Hepperle, M. Electric Flight–Potential and Limitations. In Proceedings of the Energy Efficient Technologies and Concepts of Operation, Lisbon, Portugal, 22–24 October 2012; p. 30. Available online: https://elib.dlr.de/78726 (accessed on 1 March 2024).
- Belan, M.; Arosti, L.; Polatti, R.; Maggi, F.; Fiorini, S.; Sottovia, F. A parametric study of electrodes geometries for atmospheric electrohydrodynamic propulsion. J. Electrost. 2021, 113, 103616. [Google Scholar] [CrossRef]
- He, Y.; Woolston, M.; Perreault, D. Design and implementation of a lightweight high-voltage power converter for electro-aerodynamic propulsion. In Proceedings of the 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–9. [Google Scholar] [CrossRef]
- Ilit’, T.; Vary, M.; Valko, P. On the Thrust of a Single Electrode Electrohydrodynamic Thruster. J. Electr. Eng. 2015, 66, 117–120. [Google Scholar] [CrossRef]




| Aircraft Model: | MIT | Albatross | |||
|---|---|---|---|---|---|
| Aircraft | Mass | (kg) | 2.45 | 10 | |
| Span | b | (m) | 5 | 3 | |
| Aspect ratio | 17.9 | 13.6 | |||
| Lift-over-drag | f | 8 | 28 to 30 | ||
| Battery | Mass | (kg) | 0.23 | 1.2 | |
| Energy density | (Wh) | 130 | 223 | ||
| Mission | Cruise velocity | (m) | 4.8 | 18.9 | |
| Endurance | (h) | - | 4 | ||
| Take-off | Catapulted | Catapulted or 100 m | |||
| Engine | Type | EAD, single collectors | Electric with propeller | ||
| Frontal dimensions | (m) | Diameter of 0.38 | |||
| Mass | (kg) | 0.41 | 0.29 | ||
| Thrust | (mN) | 133 (in cruise) | - | ||
| Power | (W) | 25.8 (in cruise) | - |
| Aircraft | Albatross UAV (Reference) | EAD-Propelled | ||
|---|---|---|---|---|
| EAD Albatross 1 | EAD Albatross 2 | EAD Albatross 3 | ||
| Thruster size | - | 0.28 × 0.3 × 4.3 | 0.28 × 0.3 × 2.1 | 0.28 × 0.18 × 0.9 |
| Configuration | - | dual | dual | dual |
| Thrust scaling | - | ×1 | ×2 | ×10 |
| Cruise velocity | 18.9 m | 4.5 m | 6.6 m | 18.9 m |
| Endurance | 4 h | 6 min | 42 min | 4 h |
| Ceiling | 120 m | 10 m | 10 m | 120 m |
| Available mass | 8.5 kg | 8.5 kg | 8.5 kg | 8.5 kg |
| Wingspan | 3 m | 4.3 m | 3 m | 3 m |
| Aspect ratio | 13.6 | 19.5 | 13.6 | 13.6 |
| Aircraft | Albatross (Reference) | EAD-Propelled | |||||
|---|---|---|---|---|---|---|---|
| UAV 1 | UAV 2 | UAV 3 | UAV 4 | UAV 5 | UAV 6 | ||
| Thruster size | - | 0.28 × 0.3 × 3.6 | 0.28 × 0.3 × 2.8 | 0.28 × 0.3 × 2.8 | 0.28 × 0.3 × 3.8 | 0.28 × 0.3 × 2.7 | 0.28 × 0.18 × 3.5 |
| Configuration | - | single | dual | dual | dual | dual | dual |
| Thrust scaling | - | ×1.28 | ×1.55 | ×1.55 | ×1.55 | ×3.1 | ×3.1 |
| Cruise velocity | 18.9 m | 4.8 m | 5.7 m | 5.7 m | 4.8 m | 5.7 m | 7.3 m |
| Endurance | 4 h | 46 min | 6 min | 1 h 33 min | 1 h 42 min | 4 h 10 min | 2 h 20 min |
| Ceiling | 120 m | 30 m | 30 m | 30 m | 30 m | 120 m | 30 m |
| Available mass | 8.5 kg | 6.5 kg | 8.5 kg | 6.5 kg | 6.5 kg | 6.5 kg | 6.5 kg |
| Wingspan | 3 m | 5 m | 5 m | 5 m | 5 m | 5 m | 5 m |
| Aspect ratio | 13.6 | 20 | 20 | 20 | 20 | 20 | 20 |
| Conceivable aircraft | Optimistic aircraft | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grosse, S.; Moreau, E.; Binder, N. Modeling of the Flight Performance of a Plasma-Propelled Drone: Limitations and Prospects. Drones 2024, 8, 114. https://doi.org/10.3390/drones8030114
Grosse S, Moreau E, Binder N. Modeling of the Flight Performance of a Plasma-Propelled Drone: Limitations and Prospects. Drones. 2024; 8(3):114. https://doi.org/10.3390/drones8030114
Chicago/Turabian StyleGrosse, Sylvain, Eric Moreau, and Nicolas Binder. 2024. "Modeling of the Flight Performance of a Plasma-Propelled Drone: Limitations and Prospects" Drones 8, no. 3: 114. https://doi.org/10.3390/drones8030114
APA StyleGrosse, S., Moreau, E., & Binder, N. (2024). Modeling of the Flight Performance of a Plasma-Propelled Drone: Limitations and Prospects. Drones, 8(3), 114. https://doi.org/10.3390/drones8030114










